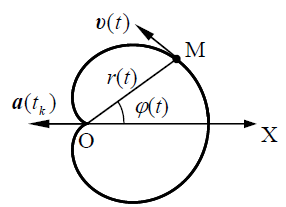
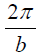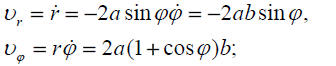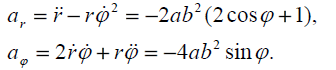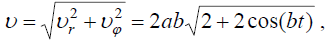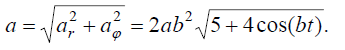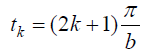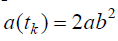ვხსნით ამოცანას მოცემულ პოლარულ კოორდინატთა სისტემაში. აღსანიშნავია, რომ M მატერიალური წერტილი მოძრაობს ჩაკეტილ ტრაექტორიაზე, პერიოდულად,  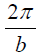პერიოდით ბრუნდება სივრცის იმავე წერტილში.

განვსაზღვროთ პოლარულ კოორდინატებში მატერიალური წერტილის სიჩქარისა და აჩქარების პროექციების დროზე დამოკიდებულება. ამისთვის გამოვიყენოთ ამოცანა 9-ში მიღებული (14) და (15) გამოსახულებები, მივიღებთ:
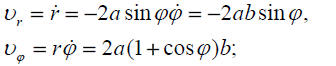(1)
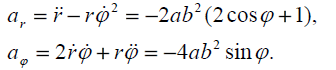(2)

მაშინ სიჩქარისა და აჩქარების მოდულები იქნება:
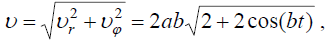(3)
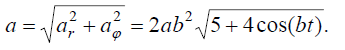(4)
აღვნიშნოთ, რომ მატერიალური წერტილი 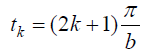დროის მომენტებში იმყოფება პოლარული კოორდინატების სისტემის სათავეში (პოლუსში), აქვს ნულოვანი სიჩქარე, ხოლო აჩქარება მოდულით ტოლია  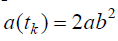(სადაცk = 0, 1, 2, ...)  და პოლარული ღერძის საპირისპიროდ არის მიმართული.