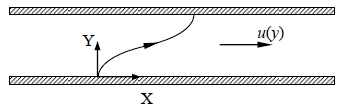
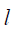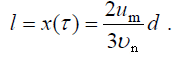I. ვირჩევთ დეკარტის კოორდინატთა სისტემას, მიმაგრებულს მდინარის ნაპირზე სათავით ნავის მდინარეში შეცურვის ადგილზე. სისტემის ღერძები და მდინარის სიჩქარის მიმართულება ნახაზზეა გამოსახული.
ამოცანის ამოხსნისას ნავს მივიჩნევთ მატერიალურ წერტილად, ხოლო მდინარის ნაპირებს ურთიერთპარალელურად.
II. ამოცანის პირობის თანახმად ნავისთვის საწყისი პირობები არის
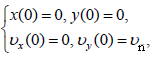
სადაც 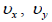
მოძრაობის სუპერპოზიციის პრინციპის თანახმად, დროის ნებისმიერ მომენტში 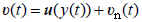
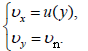
ამოცანის პირობის თანახმად მდინარის სიჩქარე პარაბოლურად არის დამოკიდებული ნაპირიდან დაშირებაზე ამიტომ შეგვიძლია ჩავწეროთ,
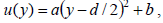
სადაც a და b – მუდმივი სიდიდეებია. -ს განსაზღვრისთვის გამოვიყენებთ ამოცანის იმ პირობას, რომ მდინარის შუაში დინების სიჩქარე მაქსიმალურია ანუ:
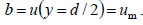
0-ში საწყისი პირობით გვაქვს
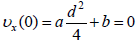
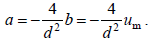
III. განტოლებათა სისტემა (2), განტოებების (3) – (5) -ის გამოყენებით მიიღებს სახეს:
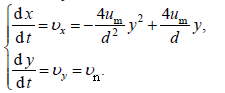
(1) საწყისი პირობების გათვალისწინებით და განტოლებების (6) ინტეგრირებით მივიღებთ მოძრაობის კანონს ანუ კოორდინატების დროზე დამოკიდებულებას:
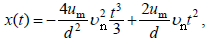
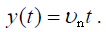
ტრაექტორიის განტოლების მისაღებად განტოლებებიდან (7) და (8) გამოვრიცხოთ დრო და მივიღებთ:
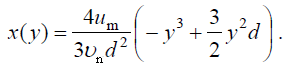
რადგან ნაპირთან მიყუდებისას 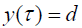
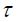
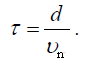
შესაბამისად წატაცების