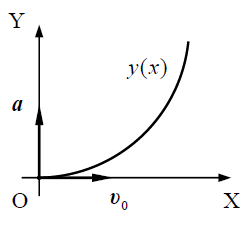
მივყვეთ მატერიალური წერტილის კინემატიკის ამოცანების ამოხსნის ზოგად სქემას.
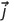I. ამოცანის პირობის თანახმად მოძრაობა მიმდინარეობს XY სიბრტყეში, რომელიც შექმნილია კოორდინატთა X და Y ღერძებით და მათი მიმართულებები განისაზღვრება შესაბამისად   და  ორტებით.

II. ჩავწეროთ არჩეულ კოორდინატთა სისტემაში საწყისი პირობები და სხეულის სიჩქარის ცვლილების კანონი მდგენელებში:

                      (1)

                   (2)

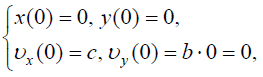
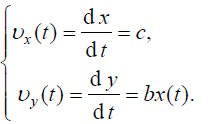
III. (2) დიფერენციალური განტოლებები, (1) საწყის პირობების გათვალისწინებით საშუალებას იძლევა მოვზებნოთ მატერიალური წერტილის მოძრაობის კანონი კოორდინატთა ღერძებზე პროექციებით და რადიუს ვექტორის დროზე დამოკიდებულება:

                       (3)

                 (4)

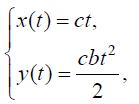
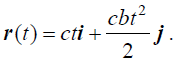
ნაპოვნი (4) გამოსახულების გამოყენებით განვსაზღვროთ  სიჩქარისა და  აჩქარების ცვლილების კანონები:

               (5)

                (6)

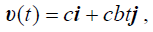
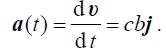
ტრაექტორიის განტოლება მოიძებნება მატერიალური წერტილის მოძრაობის კანონიდან (3)-დან  t დროის გამორიცხვით:

                  (7)

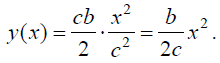
სიჩქარის მოდული განისაზღვრება ასე:

                     (8)

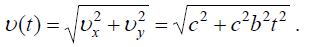
აჩქარების ტანგენციალური და ნორმალური მდგენელები შესაბამისად:

                        (9)

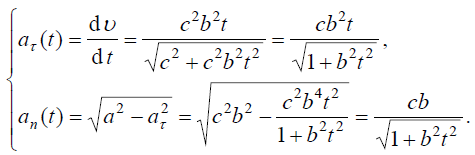
ტრაექტორიის სიმრუდის რადიუსი ასეთია:

                     (10)

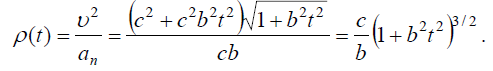
სიჩქარესა და აქარებას შორის კუთხე იქნება:

             (11)