ამოცანუს ამოხსნისას პლანეტასა და მზეს მივიჩნებთ მატერიალურ წერტილებად. კეპლერის პირველი კანონის თანახმად ყველა პლანეტა ბრუნავს ელიფსურ ორბიტებზე, ამსთან მზე იმყოფება ელიფსის ერთ-ერთ O ფოკუსში.
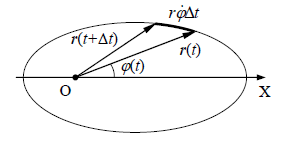
ამოცანის პირობის შესაბამისად შემოვიტანოთ პოლარული კოორდინატთა სისტემა პლანეტის მოძრაობის სიბრტყეში და მისი პოლუსი დავამთხვიოთ მზის მდებარეობას, ხოლო პოლარული ღერძი ემთხვევა ელიფსის ერთ-ერთ ღერძს. კეპლერის მეორე კანონის თანახმად პლანეტის σ სექტორული სიჩქარე, რომელიც ტოლია მატერიალური წერტილის (პლანეტის) რადიუს-ვექტორის მიერ შემოწერილი ფართობის ცვლილებისა, არის მუდმივი სიდიდე პლანეტის მზის ირგვლივ მოძრაობისას.
პოლარულ კოორდინატთა სისტემაში პლანეტის აჩქარების პროექციის მოსაძებნათ გამოვიენოთ ამოცანა 9-ში მიღებული ფორმულა (15):
(1)
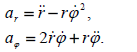
რადგან (1) განტოლებაში შედის პოლარული კოორდინატების დროითი წარმოებულები დავამატოთ ამ განტოლებას ტრაექტორიის განტოლება და გამოსახულება σ სექტორული სიჩქარისთვის:
(2)
(3)
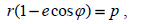
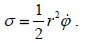
ამოცანის პირობის შესაბამისად σ სექტორული სიჩქარე მუდმივია პლანეტის ელიფსურ ტრაექტორიაზე მოძრაობისა, ამიტომ მისი დროითი წარმოებული ნულია:
(4)
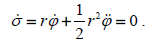
შევადაროთ (4) გამოსახულებას (1). ვხედავთ, რომ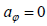 
. შესაბამისად, აჩქარებას დროის ნებისმიერ მომენტში აქვს მხოლოდ 
მდგენელი, რომელიც (1)-ის თანახმად არის პოლარული კოორდინატების წარმოებულების ფუნქცია.
გავაწარმოოთ დროით (2) განტოლების ორივე მხარე.
(5)
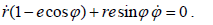
განტოლებების (2) და (3) გამოყენებით გარდავქმნათ განტოლება (5) შემდეგი სახით:
(6)
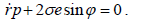
გავაწარმოოთ (6)-ის ორივე მხარე დროით
(7)
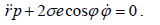
ისევ გამოვიყენოთ განტოლებები (2) და (3) რათა გამოვრიცხოთ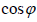 
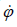
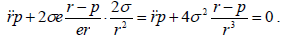
და 
(7) განტოლებიდან:
(8)
შედეგად მივიღებთ:
(9)
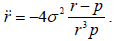
რათა ვიპოვნოთ აჩქარების პროექცია ar, როგორც მხოლოდ პოლარული კოორდინატების ფუნქცია ჩავსვათ 
(8) გამოსახულებიდან და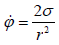 
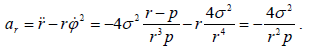
(იხ. (3)) გამოსახულებაში (1):
(10)
ამდენად, მზის ირგვლივ ელიფსურ ტრაექტორიაზე მოძრავი პლანეტის აჩქარება მიმართულია მზისკენ, არ არის დამოკიდებული პოლარულ კუთხეზე და უკუპროპორციულია მზემდე მანძილის კვადრატისა:
(11)