{loadnavigation}
რეზერფორდის მიერ წამოყენებული ატომის პლანეტარული მოდელი იყო სხეულების მოძრაობის კლასიკური წარმოდგენების ატომის მასშტაბის მოვლევებში გამოყენების მცდევობა. ის მცდელობა ხელმოცარული აღმოჩნდა. კლასიკური ატომი არამდგრადია. ორბიტაზე აჩქარებით მოძრავი ელექტრონები, ელექტრომაგნიტურ ტალღის გამოსხივევისას დახარჯავენ რა მთელ ენერგიას, აუცილებლად უნდა დაეცენენ ბირთვზე (ნახ. 1).
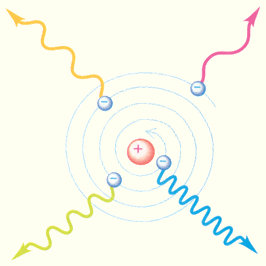
ნახ. 1.
კლასიკური ატომის არამდგრადობა
შემდეგი ნაბიჯი ატომის აგებულებზე წარმოდგენის განვითარებაში 1913 წელს გადადგა დანიელმა ფიზიკოსმა ნილს ბორმა. გაანალიზა რა ყველა ცდისეული ფაქტი, ბორი მივიდა დასკვნამდე, რომ ატომური სისტემების ყოფაქცევის აღწერისას კლასიკური ფიზიკის ბევრ კონცეფციაზე უნდა ითქვას უარი. მან ჩამოაყალიბა პოსტულატები, რომლებსაც უნდა აკმაყოფილებდეს ახალი თეორია ატომის აგებულების შესახებ.
ბორის პირველი პოსტულატი (სტაციონალური მდგომარეობების პოსტულატი) ამბობს: ატომური სისტემა შეიძლება იმყოფებოდეს მხოლოდ გარკვეული En ენერგიის შესაბამის, განსაკუთრებულ სტაციონალურ ან ქვანტურ მდგომარეობაში, სტაცოინალურ მდგომარეობაში ატომი არ ასხივებს.
ეს პოსტულატი პირდაპირ ეწინააღმდეგება კლასიკურ მექანიკას, რომელიც მიხედვითაც მოძრავი ელექტრონის ენერგია ნებისმიერი შიძლება იყოს. ის წინააღმდეგობაშია ელექტროდინამიკასთანაც, რადგანაც ეს უკანასკნელი დასაშვებად მიიჩნევს, რომ აჩქარებულად მოძრავი ელექტრონები არ ასხივებდეს ელექტრომაგნიტურ ტალღას. ბორის პირველი პოსტულატის მიხედვით ატომი ხასიათდება ენერგეტიკული დონეების სისტემით, რომლებიც გარკვეულ სტაციონალურ მდგომარეობას შეესაბამებიან (ნახ. 2). დადებითად დამუხტული ბირთვის გარშემო წრიულ ორბიტაზე მოძრავი ელექტრონის მექანიკური ენერგია უარყოფითია. ამიტომაც ყველა სტაციონალურ მდგომარეობას შეესაბამება En < 0 ენერგია. როცა En ≥ 0 ელექტრონი სცილდება ბირთვს, ე.ი. იონიზაცია ხდება. |E1| სიდიდეს იონიზაციის ენერგია ეწოდება. E1 ენერგიის შესაბამის მდგომარეობას ატომის ძირითადი მდგომარეობა ეწოდება.
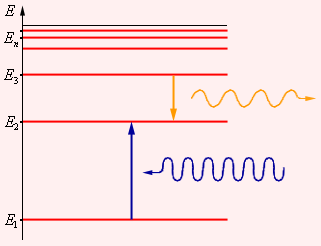
ნახ. 2.
ატომის ენერგეტიკული დონეები და ფოტონების შთანთქმისა და გამოსხივების პროცესების პირობითი გამოსახულება
ბორის მეორე პოსტულატი (სიხშირეების წესი) შემდეგნაირადაა ჩამოყალიბებული: En ენერგიის მქონე ერთი სტაციონალური მდგომარეობიდან მეორე Em ენერგიის მქონე მდგომარეობაზე გადასვლისას გამოსხივდება ან შთაინთქმება ქვანტი, რომლის ენერგია ამ სტაციონალურ მდგომარეობათა ენერგიების სხვაობის ტოლია:
hνnm = En – Em,
სადაც h – პლანკის მუდმივაა. აქედან შეიძლება გამოვსახოთ გამოსხივების სიხშირე:
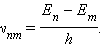
ბორის მეორე პოსტულატიც ეწიმააღმდეგება მაქსველიდ ელექტროდინამიკას, რადგანაც გამოსხივების სიხშირე განისაზღვრება მხოლოდ ატომის ენერგიის იცვლებით და არანაირად არაა დაკავშირებული ელექტრონის მოძრაობის ხასიათზე.
ბორის თეორია ატომური სისტემების ყოფაქცევის აღწერისას კლასიკურ ფიზიკას მთლიანად არ უარყოფს. მასში შენახულია წარმოდგენა ბირთვის კულონურ ველში ელექტრონების ორბიტული მოძრაობის შესახებ. რაზერფორდის კლასიკური ატომური მოდელი ბორის თეორიაში შეივსო ელექტრონული ორბიტების დაქვანტვის იდეით. ამირომ ბორის თეორიას ხანდახან ნახევრადკლასიკურს უწოდებენ.
{loadnavigation}
დაგროვილი ექსპერიმენტული მონაცემების საფუძველზე ატომის მოდელის პირველი მცდელობა ჯოზეფ ტომსონს ეკუთვნის (1903 წ.). ის თვლიდა, რომ ატომი 10–10 მ-ს რადიუსის მქონე სფეროს ფორმის ელექტრონეიტრალურ სისტემას წარმოადგენდა. ატომის დადებითი მუხტი თანაბრად იყო განაწილებული ატომის მთელ მოცულობაში, ხოლო უარყოფითად დამუხტული ელექტრონები მის შიგნით მდებარეობენ (ნახ. 1). ატომის გამოსხივების ხაზოვანი სპექტრის ასახსნელად ტომსონი ცდილობდა განესაზღვრა ატომში ელექტრონების განლაგება და მათი წონასწორული მდებარეობის მიმართ რხევის სიხშირის გათვლა. მაგრამ ეს მცდელობა წარმატებით ვერ დამთვრდა. რამდენიმე წლის შემდეგ დიდი ინგლისელი ფიზიკოსის ე.რეზერფორდის ცდებით იქნა დამტკიცებული, რომ ტომფსონის მოდელი არ იყო სწორი.

ნახ. 1.
ატომის ტომსონის მოდელი
ატომის შინაგანი სტრუქტურის კვლევის პირდაპირი პირველი ექსპერიმენტები რეზერფორდისა და მისი თანამშრომლებს ე.მარსდენსა და ჰ.გეიგერს ეკუთნოდა (1909-1911 წწ.). რეზერფორდმა გადაწყვიტა ატომების ზონდირებისთვის გამოეყენებიბა α-ნაწილაკები, რომლებიც რადიუმის და ზოგიერთი სხვა ელემენტის რადიოაქტიური დაშლისას მიიღებიან. α-ნაწილაკი ელექტრონზე დაახლოებით 7300-ჯერ უფრო დიდი მასისაა, ხოლო მისი დადებითი მუხტი გაორმაგებული ელემენტარული მუხტის ტოლია. თავის ცდებში რეზერფორდი 5 მევ-ს ტოლი კინეტიკური ენერგიის მქონე α-ნაწილაკებს (ასეთი ნაწილაკის სიჩქარე ძალიან დიდია - 107 მ/წმ-ს რიგისაა, მაგრამ სინათლის სიჩქარეზე მაინც მნიშვნელოვნად ნაკლებია) იყენებდა. α-ნაწილაკები ჰელიუმის სრულად იონიზირებული ატომებია. ისინი რეზერფორდის მიერ 1899 წ. იყო აღმოჩენილი რადიიაქტივობის მოვლენის შესწავლისას. ამ ნაწილაკებით რეზერფორდმა მძიმე ელემენტების (ოქრი, ვერცხლი, სპილენძი და სხვა) ატომები დაბომბა. ატომენის შემადგენლობაში შემავალი ელექტრონები, მცირე მასის გამო შესამჩნევად ვერ ცვლიან α-ნაწილაკების ტრაექტორიას. გაბნევა, ანუ α-ნაწილაკების მოძრაობის მიმართულების ცვლილება, შეუძლია გამოიწვიოს მხოლოდ ატომის დადებითად დამუხტულმა მძილე ნაწილმა. რაზერფორდის ცდის სქმა ნახ. 2-ზეა მოცემული.

ნახ. 2.
α-ნაწილაკების გაბნევის რეზერფორდის სქემა. K – რადიოაქტიური ნივთიერების შემცველი ტყვიის კონტეინერი, Э – თუთიის სულფიტით დაფარული ეკრანი, Ф – ოქროს ფოლგა, M – მიკროსკოპი
ტყვიის კონტეინერში მოთავსებული რადიოაქტიური წყაროდან α-ნაწილაკები მიმართული იყო თხელი მეტალური ფოლგისაკენ. გაბნეული ნაწილაკები ხვდებოდნენ თუთიის სულფიტის ფენით დაფარულ ეკრანზე, რომელზეც სწრაფი დამუხტული ნაწილაკის მოხვედრას ნათება ახლავს. ეკრანზე სინტილაცია (ანტება) მოკროსკოპის დახმარებით თვალით დაიკვირვებოდა. რეზერფორდის ცდაში α-ნაწილაკების გაბნევას შეიძლება ნაწილაკების თავდაპირველი ნაკადის მიმართ სხვადასხვა φ კუთხით იქნეს დაკვირვებული. აღმოჩნდა, რომ α-ნაწილაკების უმრავლესობა მეტალის თხელ ფენაში გადის პრაქტიკულად გადახრას არ განიცდის. მაგრამ ნაწილაკების მცირე ნაწილი გადაიხრება მნიშვნელოვანი კუთხით, რომელიც 30° აღემატება. ძალიან ცოტა α-ნაწილაკი (დაახლოებით ერთი ათი ათასიდან) დაახლოებით 180° კუთხით გადაიხრება.
შედეგი რეზერფორდისთვისაც სრულიად მოულოდნელი იყო. მისი შეხედულებები მკვეთრად ეწინააღმდეგებოდა ტომსონის მოდელს, რომლის მიხედვითაც დადებითი მუხტი ატომის მთელ მოცულობაში თანაბრად უნდა ყოფილიყო განაწილებული. ასეთი განლაგებისას დადებით მუხტს არ შეუძლია ისეთი ძლიერი ველის შექმნა, რომელსაც შეუძლია α-ნაწილაკის უკუგდება. ერთგვაროვანი დამუხტული სფეროს ელექტრული ველი მაქსიმალურია მის ზედაპირზე და მცირდება სფეროს ცენტრთან მიახლოებისას. თუ იმ სფეროს რადიუსი, რომელშიც მთელი დადებითი მუხტია თავმოყრილი, n -ჯერ შეცირდება, α-ნაწილაკზე მომქმედი უკუგდების მაქსიმალური ძალა, კულონის კანონის თანახმად გაიზრდენა n2-ჯერ. აქედან გამომდინარე, საკმარისად დიდი n-სთვის α-ნაწილაკები შეიძლება განიცდიდეს გაბნევას დიდი კუთხეებით, 180°-მდეც კი. ამ მოსაზრებებმა რეზერფორდი მიიყვანა დასკვნამდე, რომ ატომი თითქმის ცარიელია, და მთელი მისი დადებითი მუხტი მცირე მოცულობაშია თავმოყრილი. ატომის ამ ნაწილს რეზერფორდმა ატომის ბირთვი უწოდა. ასე შეიქმნა ატომის ბირთვული მოდელი. ნახ. 3 ტომსონისა და რეზერფორდის ატომებზე α-ნაწილაკების გაბნევას უჩვენებს.

ნახ. 3.
α-ნაწილაკის გაბნევა (a) ტომსონისა და (b) რეზერფორდის ატომებზე
ამგვარად, რაზერფორდის და მისი თანამშრომლების ცდების შედეგად მიღებული იქნა დასკვნა, რომ ატომის ცენტრში მოთავსებულია მკვრივი დადებითად დამუხტული ბირთვი, რომლის დიამეტრი 10–14–10–15 მ-ს არ აღემატება. ეს ბირთვი ატომის მთელი მოცულობის 10–12 ნაწილს იკავებს, მაგრამ მოიცავს მთელ დადებით მუხტს და მისი მასის 99,95 % -ს. ატომის ბირთვის შემადგენელი ნივთიერების სიმკვრივე ρ ≈ 1015 გ/სმ3 რიგისაა. მუხტი ატომის შემადგენლობაში შემავალი ელექტრონების ჯამური მუხტის ტოლია. შემდგომში დადგინდა, რომ თუ ელექტრონის მუხტს ჩავთვლით ერთეულის ტოლად, მაშინ ატომის ბირთვის მუხტი მენდელეევის ცხრილში მისი ნომრის ტოლია.
რეზერფორდის ცდებიდან გამომდინარე რადიკალურმა დასკვნებმა ატომის აგებულების შესახებ მევრი მეცნიერის უნდობლობა გამოიწვია. გამონაკლის არც თვით რეზერფორდი წარმოადგენდა, რომელმაც თავისი შედეგები თავისი პირველი ექსპერიმენტის ჩატარებიდან ორი წლის შემდეგ, მხოლოდ 1911 წელს გამოაქვეყნა. მიკროელემენტების მოძრაობის კლასიკურ წარმოდგენებზე დაყრდნობით რეზერფორდმა წარმოადგინა ატომის პლანეტარული მოდელი. ამ მოდელის მიხედვით, ატომის ცენტრში მოთავსებულია დადებითად დამუხტული ბირთვი, რომელშიც თითქმის მთელი მასაა თავმოყრილი. ატომი ზოგადად ნეიტრალურია. ბირთვის გარშემო, პლანეტის მსგავსად, ბირთვის მხრიდან კულონის ძალების მოქმედებით მოძრაობენ ელექტრონები (ნახ. 4). უძრაობის მდგომარეობაში ელექტრონს ყოფნა არ შეუძლია, რადგანაც მაშინ ისინი ბირთვზე დაეცემიან.


ნახ. 4.
რეზერფორდის ატომის პლანეტარული მოდელი
რეზერფორდის მიერ შემოთავაზებული ატომის პლანეტარული მოდელი უდავოდ დიდი ნაბიჯი იყო ატომის აგებულების შეასახებ ცოდნის განვითარებაში. ის აუცილებელი იყო α-ნაწილაკების გაბნევის ცდების ასახსნელად, მაგრამ ვერ შეძლო თვით ატომის ხანგრძლივი არსებობის ახსნა, ანუ მისი მდგრადობა. კლასიკური ელექტროდინამიკის კანონების მიხედვით, აჩქარებულად მოძრავი მუხტი უნდა ასხივებდეს ელექტრომაგნიტურ ტალღას, რომელსაც ენერგია მიაქვს. მოკლე დროში (10–8 წმ რიგის) რეზერფორდის ყველა ელექტრონმა უნდა დახარჯოს მთელი მისი ენერგია და დაეცეს ბირთვს.

ის, რომ ეს არ ხდება მდგრად მდგომარეობაში მყოფ ატომში, უჩვენებს, რომ ატომის შინაგანი პროცესები კლასიკურ კანონებს არ ემორჩილება.
{loadnavigation}
წარმოდგენა ატომებზე, როგორც განუყოფელ უმცირეს ნაწილაკებზე ჯერ კიდევ ანტიკურ ხანაში წარმოიშვა, მაგრამ მხოლოს XVIII საუკუნეში ა.ლავუაზიესა და სხვათა შრომების საშუალებით იქნა დამტკიცებული ატომების არსებობა. მაგრას საკითხი, მათი შინაგანი აგებულების შესახებ არც კი ისმოდა და იგი ისევ განუყოფელ ნაწილაკად რჩებოდა. XIX საუკუნეში ნივთიერების ატომური აგებულიბის შესწავლამ საგრძნობლად წაიწია წინ. 1833 წელს ელექტროლიზის მოვლენის შესწავლისას მ. ფარადეიმ დაადგინა, რომ ელექტროლიტში დენი დამუხტული ნაწილაკების, იონების, მოწესრიგებილი მოძრაობა იყო. ფარადეიმ განსაზღვრა იონის მინიმალური მუხტი, რომელსაც ელემენტარული ელექტრული მუხტი ეწოდა. მისი მიახლოებითი მნიშვნელობა e = 1,60·10–19 კ-ს ტოლი აღმოჩნდა.
ფარადეის გამოკვლევების საფუძველზე შეიძლებოდა ატომის შიგნით ელექტრული მუხტების არსებობის შესახებ დასკვნის გაკეთება.
ატომების რთული აგებულობის მნიშვნელოვან მოწმობას სპექტროსკოპული გამოკვლევები იძლეოდნენ, რომლებსაც ატომების ხაზოვანი სპექტრის აღმოჩენა მოჰყვა. XIX საუკუნის დასაწყისში აღმოაჩინეს წყალბადის ატომის გამოსხივების დისკრეტული სპექტრული ხაზები სპექტრის ხილულ უბანში. 1885 წელს ბალმერის მიერ დადგენილი იქნა ამ ხაზების ტალღის სიგრძეების დამაკავშირებელი მათემატიკური კანონზომიერებები.
1896 წელს ა. ბეკერელმა აღმოაჩინა ატომებისგან მომავალი უხილავი გამჭოლი გამოსხივება, რომელსაც რადიოაქტივობა ეწოდა. მომდევნო წლებში რადიაქტივობის მოვლენას მრავალი მეცნიერი სწავლობდა (მ.სკლადოვსკა-კიური, პ. კიური, ე. რეზერფორდი და სხვა). აღმოჩნდა, რომ რადიაქტიური ნივთიერებენის ატომები სამი სხვადსხვა ბუნების სხივებს ასხივებენ (ალფა-, ბეტა- და გამა-სხივებს). ალფა-სხივები ჰელიუმის იონების ნაკადი აღმოჩნდა, ბეტა-სხივები ელექტრონების ნაკადი, ხოლო გამა სხივები კი ხისტი რენტგენული გამოსხივების ქვანტების ნაკადი.
1897 წელს ჯოზეფ ტომსონმა ელექტრონი აღმოაჩინა და ელექტრონის მუხტის მასასთან ფარდობა e / m გაზომა. ტომსონის ცდებმა დაადასტურეს, რომ ელექტროვები ატომის შემადგენლობაში შედიან.
ამგვარად, XX საუკუნის დასაწყისისთვის ყველა ექსპერიმენტული ფაქტის საფუძველზე შეიძლებოდა დასკვნის გაკეთება, რომ ნივთიერების ატომებს რთული შინაგანი აგებულება აქვთ. ისინი ელექტრონეინრალურ სისიტემებს წარმოადგენენ, ამასთან ატომის უარყოფითი მუხტის მატარებელ ნაწილაკებს მსუბუქი ელექტრონები წარმოადგენენ, რომელთა მასა ატომის მასის მხოლოდ მცირე ნაწილს წარმოადგენს. ატომის მასის ძირითადი ნაწილი დადებით მუხტთანაა გაკავშირებული.
მეცნიერების წინაშე დაისვა ატომის აგებულების საკითხი.
{loadnavigation}
1923 წელს მოხდა ღირსშესანიშნავი ამბავი, რომელმაც საგრძნობლად დააჩქარა ქვანტური ფიზიკის განვითარება. ფრანგმა მეცნიერმა ლ. დე ბროილილმა წამოაყენა ჰიპოთეზა კორპოსკულურ-ტალღური დუალიზმის უნივერსალობის შესახებ. დე ბროილი ამტკიცებდა, რომ არა მარტო ფოტონებს, არამედ ელექტრონებსაც და მატერიის ნებისმიერ სხვა ნაწილაკებს კორპოსკულურის გარდა ტალღური თვისებებიც აქვთ.
დე ბროილის მიხედვით, ყოველ მიკრონაწილაკთან დაკავშირებულია, ერთის მხრივ, კორპუსკულური მახასიათებლები – ენერგია E და იმპულსი p , მეორე მხრივ კი, ტალღური მახასითებლები – სიხშირე ν და ტალღის სიგრძე λ.
მიკროობიქტების კორპუსკულური და ტალღური მახასიათებლები ისეთივე თანაფარდობებით არიან დაკავშირებულნი, როგორითაც ფოტონები:

დე ბროილის ჰიპოთეზა ამ თანაფარდობას მიაწერდა ყველა მიკრონაწილაკს, მათ შორის ისეთებსაც, რომლებსაც m მასა აქვთ. ნებისმიერი იმპულსის მქონე ნაწილაკს უსაბამებდა λ = h / p ტალღის სიგრძის მქონე ტალღურ პროცესს. მასის მქონე ნაწილაკებისათვის
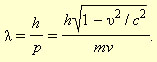
რელატივისტურ მიახლოებაში (υ << c)
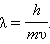
დე ბროილის ჰიპოტეზა მატერიის თვისებების სიმეტრიულობის მოსაზრებას ემყარებოდა და იმ დროისათვის ცდისუელი დადასტურება არ გააჩნდა. მაგრამ ის ძლიერ რევოლუციური ბიძგი შეიქნა ბუნების შესახებ ახალი წარმოდგენების განვითარებაში. რამოდენიმე წლის განმავლობაში XX საუკუნის გამოჩენილი ფიზიკოსების მთელმა წყებამ - ჰაიზენბერგმა, შრედინგერმა, დირაკმა, ბორმა და სხვებმა - დაამუშავეს თეორიოლი საფუძვლები ქვანტურ მექანიკად წოდებული ახალი მეცნიერებისა.
დე ბროილის ჰიპოტეზის პირველი ექსპერიმენტული დადასტურება 1927 წელს ამერიკელი ფიზიკოსის კ.დევისონის და ჯ.ჯერმერის მიერ იქნა მიღებული. მათ, შენიშნეს, რომ ნიკელის კრისტალზე გაბნეული ელექტრონების ნაკადი მკაფიო დიფრაქციულ სურათს იძლევა, როგორიც მოკლეტალღოვანი რენტგენული გამოსხივების კრისტალზე გაბნევისას მიიღება. ამ ექსპერიმენტებში კრისტალი ბუნებრივი დიფრაქციული მესერის როლს სარულებდა. დიფრაქციული მაქსიმუმების მდებარეობების მიხედვით განისაზღვრა ელექტრონული ნაკადის ტალღის სიგრძე, რომელი დე ბროილის მიერ გამოთვლილთა სრულ თანხმობაში აღმოჩნდა.
შემდეგ 1928 წელს ინგლისელმა ფიზიკოსმა ჯორჯ ტომსონმა (ელექტრონის არმომჩენი ჯოზეფ ტომსონის შვილმა) დე ბროილის ჰიპოტეზის ახალი დადასტურება მიიღო. თავის ექსპერიმენტებში (ნახ. 1) ის დიფრაქციულ სურათს აკვირდებოდა, რომელიც ოქროს თხელ პოლიკრისტალურ ფოლგაში (ფირფიტაში) ელექტრონების ნაკადის გავლი დროს იქმნებოდა.
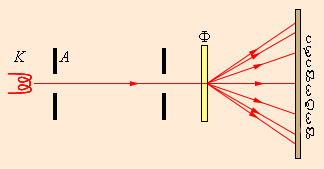
ნახ. 1.
ელექტრონების დიფრაქციის ტომსონისეული ცდის გამარტივებული სქემა. K – გახურებული კათოდი, A – ანოდი, Ф – ოქრის ფოლგა
ფოლგის უკან მოთავსებულ ფოტოფირფიტაზე გარკვევით დაიკვირვებოდა კონცენტრული ნათელი და ბნელი რგოლები, რომელთა რადიუსები დე ბროილლის თანახმად ელექტრონების სიჩქარის (ე.ი. ტალღის სიგრძის) ცვლილებასთან ერთად იცველებოდა (ნახ. 2).

ნახ. 2.
პოლიკრისტალურ ნიმუშზე ელექტრონების დიფრაქციის სურათი ხანგრძლივი ექსპოზიციის დროს (a) და მოკლე ექსპოზიციის დროს (b). შემთხვევაში ჩანს წერტილები, რომლების ცალკეული ელექტრონების ფოტოფირფიტაზე მოხვედრის კვალს წარმოადგენენ
მომდევნო წლებში ტომსონის ცდა არაერთხელ გაიმეორეს იგივე შედეგით, მათ შორის ისეთ პირობებში, როცა ელექტრონების ნაკადი იმდენად სუსტი იყო, რომ ხელსაწყოში ერთდროულად მხოლოს ერთ ნაწილაკს შეეძლო გავლა. ამგვარად, ექსპერიმენტულად იქნა დამტკიცებული, რომ ტალღური ბუნება ახასიათებს არა მარტო ელექტრონების დიდ ერთობლიობას, არამედ თითოეულ ელექტრონსაც ცალ-ცალკე.
შემდგომში დიფრაქციული თვისება აღმოაჩნდა ნეიტრონებს, პროტონებს, ატომებისა და mოლეკულების კონებს (ნაკადებს). მიკრიელემენტების ტალღური ბუნების ექსპერიმენტულმა დასაბუთაბამ შესაძლებელი გახადა დასკვნის გაკეთება, რომ ეს ბუნების უნივერსალური მოვლევა მატერიის საერთო თვისებაა. აქედან გამომდინარე, ტალღური ბუნება მაკროსკოპულ სხეულებსაც უნდა ახასიათებდეს. მაგრამ მაკროსკოპული სხეულების დიდი მასების გამო მათი ტალღური თვისების ექსპერიმენტული აღმოჩენა შეუძლებელია. მაგალითად, 10–9 გ მასის მტვრის ნაწილაკებს, რომლებიც 0,5 მ/წმ სიჩქარით მოძრაობენ შეესაბამება 10–21 მ რიგის ტალღის სიგრძის დე ბროილის ტალღა, ე.ი. ატომის ზომაზე დაახლოებით 11 რიგით ნაკლები. ასეთი ტალღის სიგრძე დაკვირვების შესაძლებლობის მიღმა უბანში მდებარეობს. ეს მაგალითი უჩვენებს, რომ მაკროსკოპულ სხეულებს მხოლოდ კორპუსკულური ბუნების გამოვლენა შეიძლიათ.
განვიხილოთ კიდევ ერტი მაგალითი. U = 100 В პოტენციალთა სხვაობით აჩქარებული ელექტრონისათვის დე ბროილის ტალღის სიგრძე შეიძლება გამოითვალოს ფორმულით
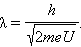
ეს არარელატივისტური შმთხვევაა, რადგანაც ელექტრონის კინეტიკური ენერგია eU = 100 ევ ბევრად მეტია უძრაობის ენერგიაზე mc2 ≈ 0,5 მევ. გათვალა იძლევა λ ≈ 0,1 ნმ-ს ტოლ მნიშვნელობას, ე.ი. ტალღის სიგრძე ზუსტად ატომის ზომის რიგისა აღმოჩნდა. ასეთი ელექტრონებისათვის კრისტალური ნივთიერება კარგ დირაქციულ მესერს წარმოადგენს. სწორედ ელექტრონების დიფრაქციის ცდებში სწორედ ასეთი ნაკლებენერგიული ელექტრონები იძლევიან მკვეთრ დიფრაქციულ სურათს. ამავე დროს ასეთი ელექტრონი, განიცდის გაბნევას კრისტალზე როგორც ტალღა, ფოტოფირფიტის ატომებთან ურთიერთქმედებს როგორც ნაწილაკი და იწვევს ფოტოემულსიის გაშავებას რაღაც გარკვეულ წერtილში (ნახ. 2).
ამგვარად, დე ბროილის ექსპერიმენტულად დამტკიცებულმა ჰიპოთეზამ კორპუსკულარულ-ტალღური დუალიზმის შესახებ მიკტოებიექტების თვისებებზე წარმოდგენა ძირეულად შეცვალა.
ყველა მიკროობიექტს ახასიათებს როგორს ტალღური, ასევე კორპუსკულური თვისებები, მაგრამ ისინი კლასიკური გაგებით არც ტალღას და არც ნაწილაკს არ წარმოადგენენ. მიკროობიექტის გავსხავვებული თვისებები ერთდროულად არ ვლინდება; ისინი ერთმანეთს ავსებენ, და მიკროობიექტს სრულად მხოლოდ ერთობლივად ახასიათებენ. ამაში მდგომარეობს დანიელი ფიზიკოსის ნ.ბორის მიერ ჩამოყალიბებული შევსებადობის პრინციპი. შეიძლება ითქვას რომ მიკროობიექტები ვრცელდებიან როგორც ტალღები და ენერგიას ცვლიან როგოორც ნაწილაკები.
ტალღური თეორიის თვალსაზრისით, ელქტრონების დიფრაქციის სურათის მაქსიმუმები დე ბროილის ტალღის უდიდეს ინტენსივობას შეესაბამება. ფოტოფირფიტაზე დარეგისტრირებულ მაქსიმუმის უბნებში ელექტრონების ყველაზე დიდი რაოდენობა ხვდება. მაგრამ ფოტოფირფიტაზე ელექტრონების სხვადასხვა ადგილას მოხვედრის პროცესი ინდივიდუალური არ არის. პრინციპულად შეუძლებელია წინასწარმეტყველება გაბნევის შემდეგ სად მოხვდება შემდეგი ელექტრონი, არსებობს მხოლოდ რაღაც ელექტრონის ამა თუ იმ ადგილას მოხვედრის ალბათობა. ამგვარად, მიკროობიექტების მდგომარეობის აღწერა და მის შემდგომი საქციელი მხოლოდ ალბათობის ცნებების საფუძველზე შეიძლება იქნეს მოცემული.
მიკროობიექტების აღწეისას ალბათური მიდგომის აუცილებლობა ქვანტური ფიზიკის უმნიშვნელოვანეს თავისებურბას წარმოადგენს. ქვანტურ მექანიკაში მიკროსამყაროში ობიექტის მდგომარეობის დასახასიათებლად შემოტანილია ტალღური ფუნქციის Ψ (ფსი-ფუნქციის) ცნება. ტალღური ფუნქციის მოდულის კვადრატი |Ψ|2 მიკრონაწილაკის სივრცის ერთეულოვან მოცულობაში ყოფნის ალბათობის პროპორციულია. ტალღური ფუნქციის კონკრეტული სახე იმ გარე პორობებით განისაზღვრება, რომელშიც იმყოფება მიკრონაწილაკი. კვანტური მექანიკის მათემატიკური აპარატი წინასწარ განსაზღვრულ ძალურ ველში მყოფი ნაწილაკის ტალღური ფუნქციის პოვნის საშუალებას იძლევა. დე ბროილის უკიდეგანო მონოქრომატული ტალღა იმ თავისუფალი ნაწილაკის ტალღურ ფუნქციას წარმოადგენს, რომეზეც არანაირი ძალური ველი არ მოქმედებს.
განსაკუთრებით გარკვევით დიფრაქციის მოვლენა ისეთ შემთხვევებში იჩენს თავს, როცა დაბრკოლების ზომები, რომელზედაც დიფრაქცია ხდება, ტალღის სიგრძის თანაზომადია (ერთი რიგისა არიან). ეს ნებისმიერი ფიზიკური ბუნების ტალღებს შეეხება, კერძოდ, ელექტრონულ ტალღებსაც. დე ბროილის ტალღებისთვის ბუნებრივ დიფრაქციულ მესერს წარმოსდგენსკრისტალის მოწესრიგებული სტრუქტურა, რომლის სივრცული პერიოდულობა ატომის ზომის როგისაა (დაახლოებით 0,1 ნმ). ამ ზომის დაბრკოლების(მაგალითად, ხვრელი გაუმჭვირვალე ეკრანში) ხელოვნურად შექმნა შეულებელია, მაგრამ დე ბროილის ტალღის ბუნენისთვის ნათელის მოსაფენად შეიძლება აზრობლივი ექსპერიმენტის ჩატარება.
განვიხილოდ მაგალითად ელექტრონის დიფრაქცია ერთეულოვან D სიგანის ხვრელზე (ნახ. 3).
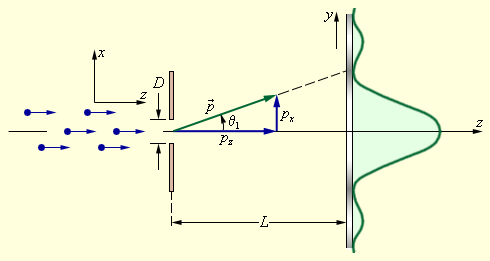
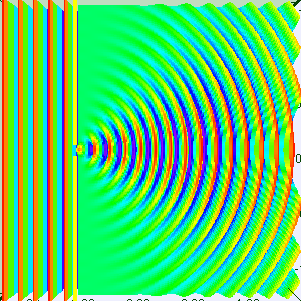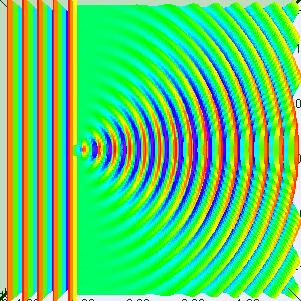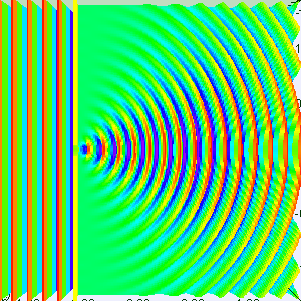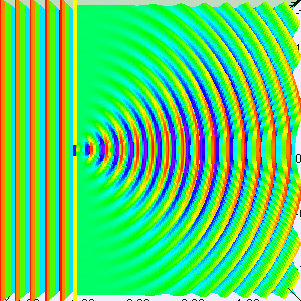
ნახ. 3.
ხვრელზე ელექტრონის დიფრაქცია. გრაფიკი მარჯვნივ - ფოტოფირფიტაზე ელექტრონების განაწილება
ხვრელში გასული ყველა ელექტრონის 85 % პროცენტი ხვდება ცენტრალურ დიფრაქციულ მაქსიმუმში. ამ მაქსიმუმის კუთხური ნახევარსიგანის პოვნა შეიძლება პირობიდან
D sin θ1 = λ.
ეს ტალღური თეორიის ფორმულაა. კორპუსკულური თვალსაზრისით შეიძლება ჩაითვალოს, რომ ხვრელში გასვლის დროს ელექტრონი მართობული მიმართულებით დამატებით იმპულსს იძენს. თუ ელექტრონების იმ 15%-ს უგულებელვყოფთ, რომელიც ფოტოფირფიტას ცენტრალური მაქსიმუმის გარეთ ხვდება, შეიძლება ჩაითვალოს, რომ მართობული იმპულსისის py მაქსიმალური მნიშვნელობა ტოლია

სადაც p – ელექტრონის სრული იმპულსია, რომელის დე ბროილის თანახმად h / λ-ს ტოლია. p-ს სიდიდე ელექტრონის ხვრელში გასვლისას არ იცვლება, რადგანაც უცვლელი რჩება ტალღის სიგრძე λ. ამ თანაფარდობებიდან გამოდის
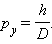
ქვანტური მექანიკა ამ გარეგნულად უბრალო თანაფარდობაში, რომელიც მიკრონაწილაკის ტალღური თვისების შედეგია, განსაკუთრებით ღრმა აზრს დებს. ელექტრონის ხვრელში გავლა წარმოადგენს ექსპერიმქნტს, სადაც ელექტრონის y –კოორდინატა განისაზღვრება Δy = D სიზუსტით. Δy სიდიდეს კოორდინატის გაზომის განუზღვრელობა ეწოდება. ამავე დროს იმპულსის y – მდგენელის განსაზღვრის სიზუსტე py-ს ტოლია ან მეტის, თუ დიფრაქციული სურათის გვერდით მაქსიმუმებსაც გავითვალისწინებთ. ამ სიდიდეს იმპულსის გეგმილის განუზღვრელობას უწოდებენ და Δpy-ით აღნიშნავენ. ამგვარად, Δy და Δpy სიდიდეები ერთმანეთთან შემდეგი თანაფარდობითაა გაკავშირებული
Δy · Δpy ≥ h,
რომელსაც ჰაიზენბერგის განუზღვრელობათა თანფარდობას უწოდებენ. Δy და Δpy სიდიდეები შემდეგნაირად უნდა გვესმოდეს, რომ მიკრონაწილაკს პრინციპში არ გააჩნია კოორდინატისა და იმპულსის გეგმილის ერთდროულად ზუსტი მნიშვნელობა. განუზღვრელობათა ფარდობა მაკრონაწილაკის კოორდინატისა და იმპულსის ერთდროული გაზომვისათვის გამოყენებული ხელსაწყოების არასრულყოფილებასთან დაკავშირებული არ არის. ის მატერიალური მიკროობიექტების ორმაგი კორპუსკულურ-ტალღური ბუნების გამოვლინებას წარმოადგენს. განუზღვრელობათა ფარდობა საშუალებას იძლევა შეფასდეს, რამდენადაა შესაძლებელი მიკრონაწილაკებისთვის კლასიკური მექანიკის მიყენება. კერძოდ, ის უჩვენებს, რომ მიკროობიექტისთვის ვერ გემოვიყენებთ ტრაექტორიის კლასიკურ ცნებას, რადგანაც ტარექტორიაზე მოძრაობა დროის ნებისმიერ მომენტში ხასიათდება კოორდინატისა და სიჩქარის გარკვეული მნიშვნელობებით. პრინციპულად შეუძლებელია იმ ტრაექტორიის მითითება, რომელზეც განსახილველ აზრობრივ ექსპერიმენტში რომელიღაც კონკრეტული ელექტრონი იმოძრავებს ხვრელის გავლიდან ფოტოფირფიტამდე.
მაგრამ, გარკვეულ პირობებში განუზღვრელობათა ფარდობა სხეულის მოძრაობის კლასიკურ აღწერას არ ეწინააღმდეგება, მათ შორის მიკრონაწილაკებისაც. მაგალითად, ტელევიზორის კინესკოპში ელექტრონების ნაკადს ელექტრონული ზარბაზნიდან გამოტყორცნის მომენტში აქვს 10–3 სმ-ს რიგის D დიამეტრი. ტელევიზორში ამაჩქარებელი ძაბვა ტოლია U ≈ 15 კვ. ელექტრონის იმპულსი ადვილი გამოსათვლელია: \(p=\sqrt{2meU}\approx\)6,6·10-23კგ·მ/წმ. ეს იმპულსი მილის (კინესკოპის) ღერძის გასწვრივაა მიმართული. განუზღვრელობათა ფარდობიდან გამოდის, ნაკადის ფორმირებისას ელექტრონებს ენიჭება გაუკონტროლებელი იმპულსი Δp, რომელიც ნაკადის ღერძის მარტობულია: Δp ≈ h / D ≈ 6,6·10–29 კგ·მ/წმ.
ვთქვათ კინესკოპის ეკრანამდე ელექტრონი გადის მანძილს L ≈ 0,5 მ. მაშინ ეკრანზე ელექტრონის ტალღური თვისებით განპირობებული ლაქის გადღაბნა როლია
\(\Delta l\approx \frac{\Delta p}{p}L\approx\)5·10–5 სმ.
რადგანაც Δl << D, ტელევიზორის კინესკოპში ელექტრონების მოძრაობის განილვა კლასიკური მექანიკის კანონებითაა შესაძლებელი. ამგვარად, განუზღვრელობათა ფარდობის საშუალებით შეიძლება გაირკვეს სამართლიანია თუ არა კლასიკური ფიზიკის კანონები ამა თუ იმ შემთხვევებში.
განვიხილოთ კიდევ ერთი აზრობრივი ექსპერიმენტი - ელექტრონების ნაკადის დიფრაქცია ორ ხვრელზე (ნახ. 4.).ამ ექსპერიმენტის სქემა იუნგის ოპტიკური ინტერფერენციის ცდის სქემას ემთხვევა.
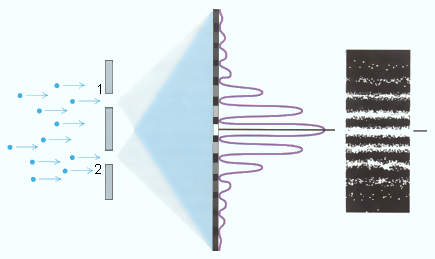

ნახ. 4.
ელექტრონების დიფრაქცია ორ ხვრელზე
ამ ექსპერიმენტის ანალიზი საშუალებას იძლევა წარმოვაჩინოთ ქვანტურ თეორიაში წარმოქმნილი ლოგიკური სირთულეები. იგივე პრობლემები წარმოიშვება იუნგის ოპტიკური ცდის ფოტონების კონცეფციის თვალსაზრისით ახსნის მცელობისას.
თუ ორ ხვრელზე ელექტრონების დიფრაქციის დაკვირვებისას ერთ ხვრელს დავფარავთ, ინტერფერენციული ზოლები ქრება და ფოტოფირფიტაზე რეგისტრირდება ერთ ხვრელზე დიფრაგირებული ელექტრონების განაწილება (ნახ. 3). ამ შემთხვევაში ეს ელექტრონები ფირფიტას აღწევენ ერთადერთი ხვრელის გავლის შემდეგ. თუ ორივე ხვრელი გახსნილია, ჩნდენბა ინტერფერენციული ზოლები, და მაშინ ისმის კითხვა, რომელი ხვრელიდან გამოფრინდა ესა თუ ის ელექტრონი ?
ფსიქოლოგიურად ძნელი შესაგუებელია, რომ ამ კითხვაზე მხოლოდ ერთი პასუხია: ელექტრონი გამოფრინდა ორივე ხვრელიდან. ჩვენ მიკრონაწილაკების ნაკადს ინტუიციურად წარმოვიდგენთ როგორც პატარა ბურთულების მიმართულ მოძრაობას და ამ მოძრაბის აღწერისთვის კლასიკური ფიზიკის კანონებს ვიყენებთ. მაგრამ ელექტრონს (და ნებისმიერ სხვა მიკრონაწილაკს) ახასიათებს არა მხილოდ კორპუსკულური, არამედ ტალღური თვისებებიც. რადგანაც ტალღა სივრცეში ლოკალიზებული არ არის, ადვილი წარმოსადგენია იუნგის ცდაში სინათლის ელექტრომაგნიტური ტალღა ორ ხვრელში როგორ გადის. მაგრამ თუ მივიღებთ ფოტონების კონცეფციას, უნდა ვაღიაროთ, რომ ყოველი ფოტონიც ასევე, არ არის ლოკალიზებული. შეუძლებელია მივუთითოთ რომელ ხვრელში გავიდა ფოტონი, ისევე როგორც შეუძლებელია ფოტოფირფიტამდე მოძრავი ფოტონის ტრაექტორიაზე თვალის მიდევნება და იმ წერტილის მითითება, რომელშიც ის მოხვდება (ფირფიტაზე). ცდა უჩვენებს, იმ შემთხვევაშიც კი, როცა ელექტრონი ინტერფერომეტრში რიგრიგობით გადის, ინტერფერენციული სურათი მრავალი დამოუკიდებელი ელექტრონის გავლის შემდეგ მაინც წარმოიქმნება. ამიტომ ქვანტური ფიზიკა ასკვნის: ფოტონი საკუთარ თავთან ინტერფერირებს.
ყოველივე ზემოთ თქმული ორ ხვრელზე ელექტრონების დიფრაქციასაც შეეხება. ცნობილი ექსპერიმენტული ფაქტების მთელი ერთობლიობა შეიძლება აიხსნას, თუ მივიღებთ, რომ ყოველი ცალკეული ელექტრონის დე ბროილის ტალღა ერთდროულად ორივე ხვრელში გადის, რის შედეგიცაა ინტერფერენცია. რიგრიგობით გამავალი ელექტრონების ნაკადიც ხანგრძლივი ექსპოზიციისას იძლევა ინტერფერენციულ სურათს, ე.ი. ელექტრონი, ფოტონის მსგავსად, საკუთარ თავთან ინტერფერირებს.
