{loadnavigation}

გეომეტრული ოპტიკის ძირითადი კანონები სინათლის ფიზიკური ბუნების დადგენამდე გაცილებით ადრე იყო ცნობილი.

სინათლი წრფივად გავრცელების კანონი: ოპტიკურად ერთგვაროვან გარემოში სინათლე წრფივად ვრცელდება. ამ კანონის ცდისეულ დასაბუთებას მკვეთრი ჩრდილების არსებობა წარმოადგენს, რომლებსაც მცირე ზომის სინათლის წყაროს („წერტილოვანი წყარო“) მიერ განათებული გაუმჭვირვალე სხეულები იძლევიან. სხვა დასაბუთებად შეიძლება გამოვიყენოთ ცნობილი ცდა, როლის დროსაც შორეული სინათლის წყაროს სხივის მცირე ზომის ჭუჭრუტანაში გასვლის შედეგად  ვიწრო სხივთა კონა წარმოიქმნება. ამ ცდას მივყავართ წარმოდგენამდე, რომ  სინათლის სხივი გეომეტრული წრფეა, რომლის გასწვრივაც ვრცელდება სინათლე. უნდა აღინიშნოს, რომ სინათლის წრფივად გავრცელების კანონი  ირღვევა და სინათლის სხივის ცნება აზრს კარგავს, თუ სინათლე ისეთ მცირე ზიმის ხვრელში გადის, რომლის ზომებიც შედარებადია სინათლის ტალღის სიგრძსთან.  ამგვარად, გეომეტრული ოპტიკა, რომელიც სინათლის სხივზე წარმოდგენას ეყრდნობა, არის ტალღური ოპტიკის ზღვრული შემთხვევა როცა λ → 0. გეომეტრული ოპტიკის გამოყენების საზღვრები სინათლის დიფრაქციისადმი მიძღვნილ თავში იქნება განხილული.

ორი გამჭვირვალე გარემოს გამყოფ ზედაპირზე სინათლე შეიძლება ნაწილობრივ აირეკლოს, ისე რომ სინათლის ენერგიის ნაწილი არეკვლის შემდეგ გავრცელდება ახალი მიმართულებით, ხოლო ნაწილი გაივლის გამყო ზედაპორს და გააგრძელებს გავრცელებას მეორე გარემოში.

სინათლის არეკვლის კანონი: დაცემული და არეკვლილი სხივები, და ასევე ორი გარემოს გამყოფი ზედაპირის სხივის დაცემის წერტილში აღმართული მართობი ერთ სიბრტყეში მდებარეობს (დაცემის სიბრტყე).   არეკვლის γ კუთხე  დაცემის  α კუთხის ტოლია.

სინათლის გარდატეხის კანონი: დაცემული და გარდატეხილი სხივები, და ასევე ორი გარემოს გამყოფი ზედაპირის სხივის დაცემის წერთილში აღმართული მართობი ერთ სიბრტყეში მდებარეობს. დაცემული α კუთხის სინუსის ფარდობა გარდატეხილი β კუთხის სინუსთან  მოცემული ორი გარემოდსათვის მუმივი სიდიდეა:

 

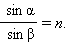
გარდატეხის კანონი ექსპერიმენტულად იქნა დადგენილი ჰოლანდიელი მეცნიერის ვ.სნელიუსის მიერ 1621 წელს.

n  მუდმივ სიდედეს უწოდებენ  მეორე გარემოს ფარდობით გარდატეხის მაჩვენებელს  პირველის მიმართ. გარემოს გარდატეხის მაჩვენებელს ვაკუუმის მიმართ აბსოლუტურ გარდატეხის მაჩვენებელს უწოდებენ.

ორი გარემოს გარდატეხის ფარდობითი მაჩვენებელი მათი აბსოლუტური მაჩვენებლების ფარდობის ტოლია:

n = n2 / n1.

არეკვლისა და გარდატეხის კანონები  ტალღური ფიზიკით აიხსნება. ტალღური წარმოდგენების თანახმად, გარდატეხა ერთი გარემოდან მეორეში გადასვლისას ტალღის გავრცელების სიჩქარის ცვლილების შედეგს წარმოადგენს. გადრატეხის მაჩვენებლის ფიზიკური არსი პირველ გარემოში ტალღის გავრცელების υ1  სიჩქარის მეორე გარემოში გარცელების υ2  სიჩქარესთან ფარდობაში მდგომარეობს:

 

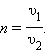
გარდატეხის აბსოლუტური მაჩვენებელი  სინათლის ვაკუუმში გავრცელების c  სიჩქარის გარემოში გავრცელების υ სიჩქარესთან ფარდობის ტოლია :

ნახ.1-ზე არეკვლისა და გარდატეხის კანონებია ნაჩვენები.

 

 ნახ. 1.

არეკვლისა და გარდატეხის კანონები: γ = α;n1 sin α = n2 sin β.

ნაკლები გარდატეხის აბსოლუტური  მაჩვენებლის  მქონე გარემოს, ოპტიკურად ნაკლებად მკვრივს უწოდებენ.

სინათლის ოპტიკურად უფრო მკვრივი გარემოდან ნაკლებად მკვრივში გადასვლისას n2 < n1 (მაგალითად, მინიდან ჰაერში) შეიძლება სრული არეკვლის, ანუ გარდატეხილი სხივის გაქრობის, მოვლენას დავაკვირდეთ. ეს მოვლენა დაიკვირვება ისეთი დაცემის კუთხეებისათვის, რომლებიც გარკვეულ კრიტიკულ αზღ კუთხეს აჭარბებენ. ამ კუთხეს სრული შინაგანი არეკვლის ზღვრულ კუთხეს უწოდებენ (ნახ. 2).

დაცემის კუთხისთვის α = αზღ  sin β = 1;  sin αზღ = n2 / n1 < 1.

თუ მეორე გარემოს ჰაერი წარმოადგენს (n2 ≈ 1), მაშინ ამ ფორმილის გადაწერა შემდეგი სახითაა მოსახერხებელი

sin αზღ = 1 / n,

სადაც n = n1 > 1 – პირველი გარემოს  გარდატეხის აბსოლუტური მაჩვენებელია.

მინა-ჰაერის გამყოფი ზედაპირისათვის (n = 1,5) კრიტიკული კუთხე αზღ = 42°, წყალი- ჰაერისათვის კი (n = 1,33) αზღ = 48,7°.

 

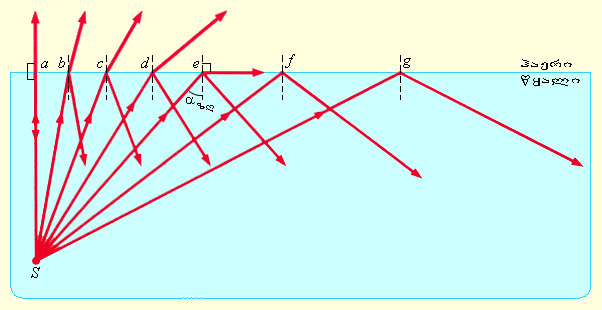
ნახ. 2.

სინათლის სრული შინაგანი არეკვლა წყლისა და ჰაერის გამყოფ ზედაპირზე; S – სინათლის წერტილოვანი წყაროა

სრული შინაგანი არეკვლის მოვლენა მრავალ ოპტიკურ ხელსაწყოში გამოიყენება. განსაკუთრებით საინტერესო და მნიშვნელოვან მაგალითი ბოჭკოვანი სინათლის გამტარების შექმნაა, რომლების ოპტიკურად გამჭვირვალე (მინა, კვარცი), წვრილ (რამოდენიმე მიკრომეტრიდან მილიმეტრამდე) მოქნილი ძაფებია. ბოჭკოვანი სინათლის გამტარების ბოლოზე მოხვედრილ სინათლე მასში, გვერდითი ზედაპირებიდან სრული შინაგანი არეკვლის ხარჯზე,  შეიძლება დიდ მანძილებზე გავრცელდეს (ნახ. 3). სამეცნიერო-ტექნიკურ მიმართულებას, რომელიც ბოჭკოვანი სინათლის გამტარების შემუშავებითა და დამზადებითაა დაკავებული, ბოჭკოვანი ოპტიკა ეწოდება.

 

 

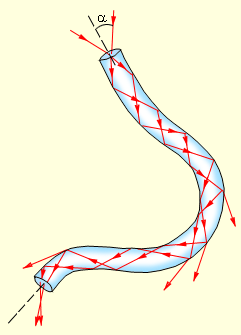
ნახ. 3.

სინათლის გავრცელება ბოჭკოვანი სინათლის გამტარში. ბიჭკოების ძლიერი გადაღუნვისას სრული შინაგანი არეკვლის კანონი ირღვევა, და სინათლე ნაწილობრივ გამოდის ბოჭკოს გვერდითი ზედაპირიდან

{loadnavigation}

ოპტიკა ფიზიკის დარგია, რომელიც სინათლის თვისებებსა და ფიზიკურ ბუნებას, აგრეთვე მის ნივთიერებებთან ურთიერთქმედებას  სწავლობს. ოპტიკა სამ ნაწილად იყოფა:

  • გეომეტრული ან სხივური ოპტიკა, რომელსაც  საფუძვლად სინათლის სხივების შესახებ სწავლება უდევს საფუძვლად;
  • ტალღური ოპტიკა, რომელიც იმ მოვლენებს სწავლობს სადაც სინათლის ტალღური ბუნება ვლინდება;
  • ქვანტური ოპტიკა, რომელიც სინათლის ნივთიერებებთან ურთიერთქმედებას სწავლობს, რომლის დროსაც სინათლის კორპუსკულური ბუნება ვლინდება.

მოცემულ თავში ოპტიკის პირველი ორი ნაწილი განიხილება. სინათლის კორპოსკულურ თვისებას შემდეგ თავში განვიხილავთ.

{loadnavigation}

ელექტრომაგნიტური ტალღების არსებობა თეორიულად დიდმა ინგლისელმა ფიზიკოსმა ჯ.მაქსველმა 1864 წელს იწინასწარმეტყველა. მაქსველმა ყველა ინდროისათვის ცნიბილი ელექტროდინამიკური კანონი გაანალიზა და ათი გამოყენება სცადა დროში ცვლადი ელექტრული და მაგნიტური ველებისათვის. მან ყურადღება მიაქცია ელექტრული და მაგნიტური მოვლენების კავშირში არსებულ ასიმეტრიას. მაქსველმა ფიზიკაში შემოიტანა გრიგალური ელექტრული ველის ცნება და ფარადეის მიერ 1831 წელს აღმოჩენილი ელექტრული ინდუქციის კანონის ახალი ინტერპრეტაცია წარმოადგინა:

მაგნიტური ველის ყოველგვარი ცვლილება გარემომცველ სივრცეში შეკრული ძალწირების მქონე გრიგალურ  ელექტრულ  ველს წარმოქმნის.   

მაქსველმავე გამოთქვა ჰიპოთეზა საწიანააღმდეგო პროცესის არსებობის შესახებ:

დროში ცვლადი ელექტრული ველი გარემომცველ სივრცეში მაგნიტურ ველს წარმოქმნის.

ნახ. 1 და 2-ზე ელექტრული ველის მაგნიტურად და პირიქით გადაქცევაა გამოსახული.

 

  

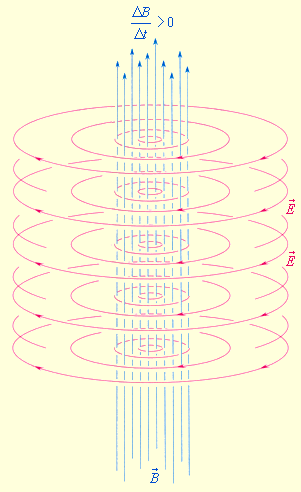
ნახ. 1.

ელექტროინდუქციის კანონი

მაქსველის ინტერპრეტაციით

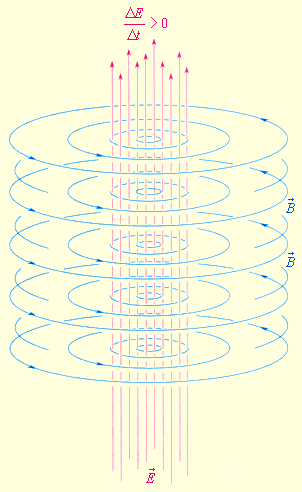
ნახ. 2.

მაქსველის ჰიპოთეზა. ელექტრული

ველის ცვლილება  მაგნიტურ

 ველს წარმოქმნის

ეს ჰიპოთეზა თეორიულ მოსაზრებას წარმოადგენდა და არ გააჩნდა ექსპერიმენტული დასაბუთება, მაგრამ მის საფუძველზე მაქსველმა შეძლო ჩაეწერა თანმიმდევრული განტოლებათა სისტემა, რომელიც აღწერდა ელექტრული და მაგნიტური ველების ურთიერთგადაქმანას (ელექტრული ველის მაგნიტურად და პირიქით გადაქცევა), ანუ ელექტრომაგნიტური ველის განტოლებათა სისტემა (მაქსველის განტოლებები). მაქსველის თეორიიდან გამომდინარეობს რიგი მნიშვნელოვანი შედეგებისა:

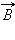1. არსებობს ელექტრომაგნიტური ტალღები, ე.ი. სივრცესა და დროში  განვრცობადი ელექტრომაგნიტური ველი. ელექტრომაგნიტური ტალღები ურთიერთმართობულია -   და  ურთიერთმართობულ სიბრტყეებში მდებარეობენ და ტალღის გავრცელების მიმართულების მართობული არიან (ნახ. 3).

 

ნახ. 3.

სინუსოიდური (ჰარმონიული) ელექტრომაგნიტური ტალღა. ვექტორები ,  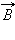 და 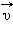 ურთიერთმართობულია

2. ელექტრომაგნიტური ტალღები ნივთიერებაში სასრული სიჩქარით ვრცელდებიან

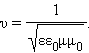
აქ ε და μ – ნივთიერების დიელქტრული და მაგნიტური შეღწევადობებია,  ε0 და μ0 – ელექტრული და მაგნიტური მუდმივები: ε0 = 8,85419·10–12 ფ/მ, μ0 = 1,25664·10–6 ჰც/მ.

სინუსოიდურ ტალღაში ტალღის სიგრძე λ ტალღის გავრცელების υ სიჩქარესთან დაკავშირებულია ფორმულით λ = υT = υ / f, სადაც  f – ელექტრომაგნიტური ველის რხევათა სიხშირეა, T = 1 / f.

ვაკუუმში ელექტრომაგნიტური ტალღის გავრცელების სიჩქარე (ε = μ = 1): 

ვაკუუმში ელექტრომაგნიტური ტალღის გავრცელების სიჩქარე c ერთ-ერთ ფუნდამენტურ ფიზიკურ მუდმივას წარმოადგენს.

მაქსველის დასკვნები ელექტრომაგნიტური ტალღის გავრცელების სასრული სიჩქარის შესახებ წინააღმდეგობაში იმყოფებოდა ინ დროისთვის მიღებულ შორსმოქმედების თეორიასთან, რომლის თანახმად ელექტრული და მაგნიტური ველების გავრცელების სიჩქარე უსასრულოდ დიდად იყო მიღებული. ამიტომ მაქსველის თეორიას ახლომოქმედების თეორიას უწოდებდნენ

3.  ელექტრომაგნიტურ ტალღაში ელექტრული და მაგნიტური ველების ურთიერთგარდაქმნა ხდება. ეს პროცესები ერთდროულად მიმდინარეობს, და ელექტრული და მაგნიტური ველები თანაბარუფლებიან „პარტნიორებს“ წარმოადგენენ. ამიტომ ელექტრული და მაგნიტური მოცულობითი სიმკვრივეები ერთმანეთის ტოლია:  wე = wм. 

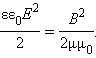
აქედან გამოდის, რომ ელექტრომაგნიტური ტალღაში მაგნიტური ველის 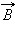ინდუქციის სიდიდე და ელექტრული ველის დაძაბულობა  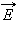სივრცის ყოველ წერტილში ერთმანეთთან დაკავშირებილია თანაფარდობით

4.  ელექტრომაგნიტურ ტალღაებს ენერგია გადააქვს. ტალღების გავრცელებისას იქმნება ელექტრომაგნიტური ენერგიის ნაკადი. თუ გამოვყოფთ ტალღის გავრცელების მართობულად ორიენტირებულ S ფართობს (ნახ. 3), მაშინ მცირე Δt  დროის განმავლობაში ამ ფართობში გაივლის ΔWEM  ენერგია, რომელიც ტოლია

ΔWEM = (wE + wM)υSΔt.

ნაკადის სიმკვრივე ან ინტენსივობა I ეწოდება ელექტრომაგნიტურ ენერგიას, რომელსაც ტალღა  დროის ერთეულში ერთეულ ფართობში გაატარებს:

wэ, wм და υ სიდიდეების გამოსახულებების ჩასმით შეიძლება მივიღოთ:

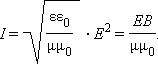
ელექტრიმაგნიტურ ტალღაში ეnერგიის ნაკადი ისეთი 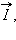 ვექტორის სახით შეიძლება აღვწეროთ, რომლის მომართულება ტალღის გავრცელების მიმართულებას ემთხვევა, ხოლო სიდიდე EB / μμ0-ს ტოლია. ემ ვექტორს პოინტინგის ვექტორს უწოდებენ.

ვაკუუმში სინუსოიდურ (ჰარმონიულ) ტალღაში ელექტრომაგნიტური ენერგიის ნაკადის სიმკვრივის საშუალო Iსაშ მნიშვნელობა ტოლია

 

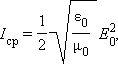
 სადაც E0 –ელექტრული ველის დაძაბულობის რხევის ამპლიტუდაა.

სი სისტემაში ნაკადის სიმკვრივე იზომება ვატებით კვადრატულ მეტრზე (ვ/მ2).  

მაქსველის თეორიიდან გამომდინარეობს, რომ ელექტრომაგნიტური ტალღები მშთანთქავ ან ამრეკლავ სხეულზე წნევით უნდა მოქმედებდნენ. ელექტრომაგნიტური ტალღების წნევა იმით აიხსნება, რომ ტალღის ელექტრული ველის გავლენით ნივთიერებაში აღიძვრება სუსტი დენები, ანუ დამუხტული ნაწილაკების მიმართული მოძრაობა. ამ დენებზე ტალღის მაგნიტური ველი ამპერის ძალით მოქმედებს, რომელიც ნივთიერების შიგნითაა მიმართული. სწორედ ეს ძალა ქმნის წნევას. ჩვეულებრივ ელექტრომაგნიტური ტალღების წნევა უმნიშვნელოდ მცირეა. ასე, მაგალითად, დედამიწამდე მოღწეული მზის გამოსხივების წნევა აბსოლუტურად მშთანთქავ ზედაპორზე დაახლოებით 5მკპასკალს შეადგენს. 

 ელექტრომაგნიტური ტალღების წნევის არსებობამ შესაძლო გახადა დასკვნა იმის შესახებ, რომ ელექტრომაგნიტურ  ველს მექანიკური იმპულსი ახასიათებს. ელექტრომაგნიტური  ველის იმპულსი ერთეულ მოცულობაში განისაზღვრება ფარდობით

სადაც  wEM – ელექტრომაგნიტური ენერგიის მოცულობითი სიმკვრივეა, c – ვაკუუმში ტალღების გავრცელების სიჩქარეა. ელექტრომაგნიტური იმპულსის არსებობა ელექტრომაგნიტური მასის ცნების შემოტანის საშუალებას იძლევა.

ერთეულოვანი მოცულობის ველისათვის

აქედან გამოდის:

ერთეულ მოცულობაში მასის  ეს ფარდობა ელექტრომაგნიტურ ენერგიასთან ბუნების უნივერსალურ კანონს წარმოასდენს. ფარდობითობის სპეციალური თეორიის თანახმად, იგი სამართლიანია ნებისმიერი სხეულისთვის მათი ბუნებისა და შინაგანი აგებულების მიუხედავად.

ამგვარად, ელექტრომაგნიტურ  ველს მატერიალური სხეულების ყველა თვისება აქვს: ენერგია, გავრცელების სასრული სიჩქარე, იმპულსი, მასა. ეს იმაზე მეტყველებს, რომ ელექტრომაგნიტური ველი მატერიის არსებობის ერთ-ერთი ფორმაა.

6. მაქსველის ელექტრომაგნიტური თეორიის პირველი ექსპერიმენტული დასაბუთება ამ თეორიის შექმნიდან 15 წლის მერე ჰ.ჰერცის 1888 წლის ცდებით მოხერხდა. ჰერცმა არა მარტო ექპერიმენტულად დაასაბუთა ელექტრომაგნიტური ტალღების არსებობა, არამედ პირველმა დაიწყო მათი თვისებების შესწავლა: სხვადსხვა გარემოს მიერ მათი შთანთქმა და გარდატეხა, მეტალური ზედაპირებიდან არეკვლა და ა.შ. მან შეძლო ცდისეულად გაეზომა ელექტრომაგნიტური ტალღების ტალღის სიგრძე და გავრცელების სიჩქარე, რომელიც სინათლის სიჩქარის ტოლი აღმოჩნდა.

ჰერცის ცდებმა უმნიშვნელოვანესი როლი შეასრულეს მაქსველის ელექტრომაგნიტური თეორიის დამტკიცებასა და აღიარებაში. ამ  ცდებიდან 7 წლის შემდეგ ელექტრომაგნიტურმა ტალღებმა   უსადენო კავშირში ჰპოვა გამოყენება.

7. ელექტრომაგნიტური ტალღები აღიძვრება მხოლოდ აჩქარებულად მოძრავ მუხტების საშუალებით. მუდმივი დენის წრედები, რომლებშიც მუხტის მატარებლები მუდმივი სიჩქარით მოძრაობენ, ელექტრომაგნიტური ტალღების წყაროს არ წარმოადგენენ. თანამედროვე რადიოტექნიკაში ელექტრომაგნიტური ტალღების გამოსხივება ხდება სხვადასხვა კონსტრუქციის ანტენების საშუალებით, რომლებშიც სწაფად ცვლადი დენები აღიძვრება.

ელექტრომაგნიტური ტალღების გამომსხივებელი უმარტივესი სისტემაა მცირე ზომის ელექტრული დიპოლი, რომლის დიპოლური მომენტი p(t) დროში სწრაფად იცვლება.

ასეთ ელემენტარულ დიპოლებს ჰერცის დიპოლებს უწოდებენ. რადიოტექნიკაში ჰერცის დიპოლი ისეთი მცირე ზომის ანტენის ექვივალენტურია, რომლიც ზომების λ ტალღის სიგრძეზე ბევრად ნაკლებია (ნახ. 4).

 

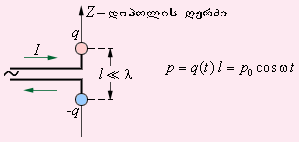
ნახ. 4

ჰარმონიულად მერხევი ელექტრომაგნიტური დიპოლი

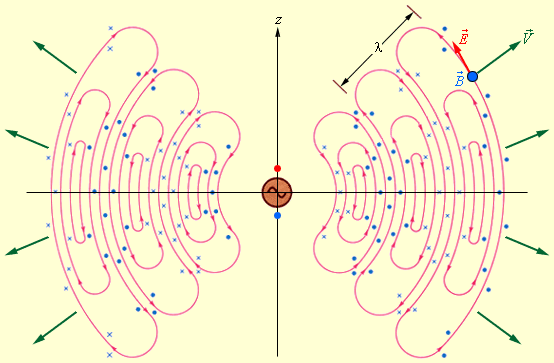
ნახ. 5.

ელემენტალური დიპოლის გამოსხივება

ნახ. 5  დიპოლის მიერ გამოსხივებული ელექტრომაგნიტური ტალღების სტრუქტურაზე იძლევა წარმოდგენას. საყურადღებოა, რომ ელექტრომაგნიტური ენერგიის მაქსიმალური ნაკადი გამოსხივდება დიპოლის ღერძის პერპენდიკულარულ სიბრტყეში. თავისი ღერძის გასწვრივ დიპოლი ენერგიას არ ასხივებს. ელექტრომაგნიტური ტალრების არსებობის დამტკიცებისას ჰერცი იყენებდა ელემენტალურ დიპოლს როგორც გამომსხივებელს და როგორც მიმღებ ანტენას.

{loadnavigation}

ცვლადი დენის ხელსაწყოებს შორის, რომლებმაც ფართო გამოყენება ჰპოვეს ტექნიკაში, მნიშვნელოვან ადგილს იკავებენ ტრანსფორმატორები . ცვლადი დენის წყაროს ძაბვის გადიდებისა ან შემცირებისათვის გამოყენებული ტრანსპორმატორების მუშაობის პრინციპი ელექტრომაგნიტური ინდუქციის პრინციპზეა დამყარებული. უმარტივესი ტრანსფორმატორი შედგება მაგნიტური მასალისაგან დამზადებული შეკრული ფორმის გულასაგან, რომელზეს ორი მავთულის გრაგნილია დახვეული: პირველადი და მეორადი (ნახ.1).

 

ნახ. 1.

უმარტივესი ტრანსფორმატორი და მისი პირობითი სქემატური გამოსახულება. n1 და n2 – ხვიეთა რიცხვებია გრაგნილში

პირველადი გრაგნილი e1 (t) ემძ-ს მქონე ცვლადი დენის წყროსთანაა მიერთებული, ამიტომ მასში აღიძვრება J1 (t) დენი, რომელიც ტრანსპორმატორის გულაში ცვლად მაგნიტურ Φ ნაკადს ქმნის. ეს ნაკადი პრაქტიკულად გაფანტვის გარეში ცირკულირებს შეკრულ მაგნიტურ გულაში და გამსჭვალავს პირველადი და მეორადი გრაგნილების ყველა ხვიას. უქმი სვლის რეჟიმში, ე.ი. როცა მეორადი გრაგნილის წრედი გახსნილია, დენი პირველად გრაგნილში საკმაოდ მცირეა გრაგნილის დიდი ინდუქციური წინაღობის გამო. ამ რეჟიმში ტრანსპორმატორი დიდ სიმძლავრეს მოიხმარს.

 სიტუაცია მკვეთრად იცვლება, როცა მეორადი გრაგნილის წრედში Rн წინაღობის მქონე დატვირთვა ირთვება, და მასში აღიძვრება ცვლადი დენი J2 (t). ახლა გულაში სრული მაგნიტურ Φ ნაკადს ორივე დენი ქმნის. მაგრამ კენცის წესის თანახმად მაგნიტური ნაკადი Φ2, რომელიც მეორად გრაგნილი ინდუქცირებული J2  დენით იქმნება, პერველად  გრაგნილში გამავალი J1დენის მიერ შექმნილი Φ1  ნაკადისშმხვედრი მიმართულებითაა მიმართული:  Φ = Φ1 – Φ2. აქედან გამოდის, რომ J1 და J2 დენების საპირისპირო ფაზებში იცვლებიან, ე.ი. ფაზის წანაცვლება 180°-ია.

მეორე მნიშვნელოვანი დასკვნა იმაში მდგომარეობს, რომ დენი პირველად  გრაგნილში J1 დატვირთვისას მნიშვნელოვნად მეტია ვიდრე  უქმი სვლის დენი. ის იმიტომ ხდება, რომ გულაში სრული ნაკადი Φ დატვირთვის რეჟიმში ისეთივე უნდა იყოს როგორც უქმი სვლის დროს, რადგან ძაბვა u1 პირველად გრაგნილზე ორივე შემთხვევაში ერთნაერია. ეს ძაბვა ცვლადი დენის წყაროს  e1  ემძ-ს ტოლია. რადგანაც გრაგნილების გამსჭვალავი მაგნიტური ნაკადი, გრაგნილებში ხვიათა n1 და n2 რიცხვების ტოლია, პირველადი გრაგნილისთვის შეიძლება ჩაიწეროს:

მეორადი გრაგნილისათვის:

აქედან გამომდინარე,

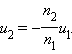
ნიშანი მინუსი ნიშნავს, რომ    u1 და u2 ძაბვები, ისევე როგორც   J1 და J2  დენები გრაგნილებში, საპირისპირო ფაზებში იმყოფებიან. ამიტომ პირველად გრაგნილში ძაბვასა u1  და დენს J1  შორის ფაზათა წანაცვლება φ1  ტოლია მეორად გრაგნილში ძაბვასა u2  და დენს J2  შორის ფაზათა φ2 წანაცვლებისა. თუ მეორე გრაგნილი დატვირთვას აქტიური Rн წინაღობა წარმოადგენს, მაშინ φ1 = φ2 = 0.

გრაგნილებზე ძაბვების ამპლიტუდური მნიშვნელობებისათვის შეიძლება ჩაიწეროს:

კოეფიციენტი K = n2 / n1  ტრანსფორმაციის კოეფიციენტია. როცა K > 1 ტარანსპორმატორს უწოდებენ ამამაღლებელს, ხოლო როცა K < 1 – დამადაბლებელს.

ზევით მოყვანილი თანაფარდობები სამართლიანია მხოლოდ იდეალური ტრანსფორმატორებისათვის, სადაც არ არისმაგნიტური ნაკადის გაბნევა და ენერგიის დანაკარგები ჯოულის სითბოზე. ეს დანაკარგები შეიძლება დაკავშირებული იყოს  თვითონ გრაგნილების აქტიური წინაღობების არსებობასთან და გულაში ინდუქციური დენების (ფუკოს დენების) წარმოქმნასთან. ფუკოს დენების შესამცირებლაგ ტრანსფორმატორის გულები ჩვეულებრივ თხელი ფოლადის, ერთმანეთისაგან იზოლირებული, ფურცლებისაგან  მზადდება. ენერგიის დაკარგვის კიდევ ერთი მექანიზმი არსებობს, რომელიც გულას ჰისტერეზისულ მოვლენასთანაა დაკავშირებული. ფერომაგნიტური მასალების ციკლური გადამაგნიტების დროს ადგილი აქვს ენერგიის დანაკარგს, რომელიც ჰისტერეზისის მარყუჟის ფართობის პირდაპირპროპორციულია.

კარგ თანამედროვე ტრანსფორმატორებში დატვირთვისას ენერგიის დანაკარგები  ნომინალურთან ახლოსაა და 1–2 %-ს არ აჭარბებს, ამიტომ მათთვის იდეალური ტრანსფორმატორის თეორია მიახლოებით სამართლიანია.

თუ ენერგიის დანაკარგებს უგულვებელვყოფთ, მაშინ ცვლადი დენის წყაროდან ტრანსფორმატორის მიერ მოხმარებული სიმძლავრე P1 დატვირთვისათვის გადაცემული P2  სიმძლავრის ტოლია.

აქედან გამოდის, რომ

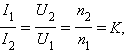
ე.ი. გრაგნილების დენები ხვიების უკუპროპორციულია.

თუ მხედველობაში მივიღებთ, რომ U2 = RнI2, შეიძლება მივიღოთ შემდეგი თანაფარდობა

ფარდობა  Rექვ = U1 / I1 შეიძლება განვიხილოთ როგორც პირველადი წრედის აქტიური წინაღობა, როცა მეორადი გრადნილი დატვირთულია Rн წინაღობით. ამგვარად, ტარნსფორმატორი გარდაქმნის არა მართო ძაბვასა და დენს, არამედ წინაღობასაც.

თანამედროვე ტექნიკაში ფართო გამოყენება ჰპოვეს სხვადასხვა კონსტრუქცის პრანსფორმატორებმა. რადიოტექნიკურ მოწყობილობებში გამოიყენება მცირე ზონის, დაბალ სიმძლავრის ტრანსფორმატორები, რომლებსაც ჩვეულებრივ რამოდენიმე გრაგნილი (ცვლადი დენი წყაროს ძაბვის ამამაღლებელი ან დამადაბლებელი) აქვთ. ელექტროტექნიკაში ხშირად გამოიყენება ე.წ. სამფაზიანი ტრანსფორმატორები, რომლებიც ერთდროულად სამი, ერთმანეთისადმი  120°-ანი კუთხის წანაცვლებული ფაზების მქონე, ძაბვის ასამაღლებლად ან დასადაბლებლადაა განკუთვნილი.

მძლავრი სამფაზიანი ტრანსფორმატორები გამოიყენება დიდ მანძილებზე ელექტროენერგიის გადაცემისათვის.

ელექტროსადგულიდან ათასობით კილომეტრით დაშორებულ დიდ ქალაქებამდე ან საწარმოო ცენტრებამდე ელექტროენერგიის გადაცემა რთულ სამეცნიერო-ტექმიკურ პრობლემას წარმოადგენს.

გამტარების გათბობაზე დანაკარგების შეამცირებლად აუცილებელია გადამცემ ხაზებძე დენის ძალის შემცირება, და ე.ი. ძაბვის გადიდება. ჩვეულებრივ გადაცემის ხაზები გათვილია 400-500კვ-ზე, ამასთან ხაზებში გამოიყენება 50ჰც სიხშირის სამფაზა დენი. ნახ. 2-ზე მოცემულია ელექტროენერგიის მომხმარებლამდე გადაცემის სქემა. სქემა წარმოდგენას იძლევა თუ როგორ ხდება ტრანსფორმატორების გამოყენება ელექტროგადაცემისას.

უნდა აღინიშნოს, რომ ძაბვის გადიდებისას გადაცემის ხაზებში იზრდება ჰაერის საშუალებით ენერგიის გადინება. ტენიან დღეებში გამტარების მახლობლობაში შეიძლება წარმოიშვეს ე.წ. კორონალური განმუხტვა, რომელიც შეიძლება დამახასიათებელი ტკაცუნის საშუალებით გამოვლინდეს. გადაქემის ხაზების მარგი ქმედების კოეფიციენტი 90 %-ს არ აღემატება.

 

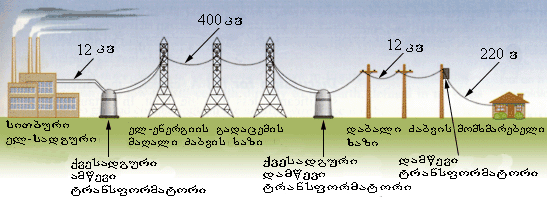
ნახ. 2.

მაღალი ძაბვის ელექტროგადამცემი ხაზების პირობითი სქემა. ტრანსფორმატორები ძაბვას ხაზის რამდემიმე წერტილშიცვლიან. სქემაზე მაღალი ძაბვის ელექტროგადამცემი ხაზის სამი სადენიდან მხოლოდ ერთია გამოსახული