{loadnavigation}
თანამედროვე ელექტრონულ ტექნიკაში თანამედროვე ნახევარგამტარული ხელსაწყოები გადამწყვეტ როლს ასრულებენ. ბოლო სამი ათწლეულის განმავლობაში მათ თითქმის სრულად გამოდევნეს ელექტროვაკუუმური ხელასაწყოები.
ნებისმიერ ნახევარგამტარულ ხელსაწყოს აქვს ერთი ან ორ ელექტრონულ-ხვრელური გადასასვლეი. ელექტრონულ-ხვრელურ გადასასვლელი (ან n–p-გადასასვლელი) ორი სხვადასხვა გამტარობის ნახევარგამტარის კონტაქტის არეა.
n-ტიპის ნახევარგანტარში თავისუფალი მუხტის ძირითად მატარებელს ელექტრონი წარმოადგენს; მათი კონცენტრაცია ხვრელების კონცენტრაციას მნიშვნელოვნად აჭარბებს (nn >> np). p-ტიპის ნახევარგანტარში თავისუფალი მუხტის ძირითად მატარებელს ხვრელები წარმოადგენენ (np >> nn). ორი n- და p-ტიპის ნახევარგამტარის კონტაქტისას დიფუზიის პროცესი იწყება: ხვრელები p-არეებიდან გადადიან n-არეებში, ელექტრონები კი პირიქით, n-არეებიდან გადადიან p-არეებში. ამის შედეგად n-არეები კონტაქტის ზონის მახლობლად ელექტრონების კონცენტრაცია კლებულობს და წარმოიქმნება დადებითად დამუხტული ფენა. p-არეში კლებულობს ხვრელების კონცენტრაცია და წარმოიქნმება ორმადი ელექტრონული ფენა, რომელიც ეწინააღმდეგება ელექტრონებისა და ხვრელების ერთმანეთისკენ დიფუზიის პროცესს (ნახ. 1). სხვდასხვა გამტარობის ნახევარგამტარების გამყოფი სასაზღვრო არე (ე.წ. ჩამკეტი ფენა) ჩვეულებრივ აღწევს ათეულობით და ასეულობით ატომებს შორისი მანძილის რიგის სისქეს. ამ ფენის მოცულობის მუხტები n- და p-არეებს შორის ქმნიან ჩამკეტ ძაბვას Uჩ, რომელიც გერმანიუმის n–p-გადასასვლელისათვის 0,35 ვ ტოლია, ხოლო სილიციუმისათვის 0,6 ვ.
n–p-გადასასვლელის გასაოცარი თვისებაა ცალმხრივი გამტარობა.
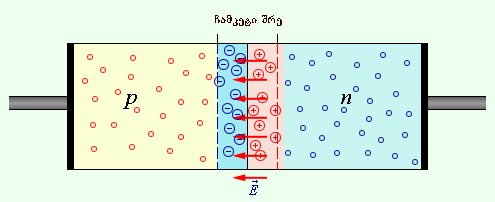
ნახ. 1.
p- და n-ტიპის ნახევარგამტარების კონტაქტის დროს ჩამკეტი ფენის წარმოქმნა
თუ n–p-გადასასვლელის ნახევარგამტარს დენის წყაროს ისე მივუერთებთ, რომ წყაროს დადებითი პოლუსი მიერთებულია n-არეს, ხოლო უარყოფითი p-არეს, მაშინ ჩამკეტ ფენაში ველის დაძაბულობა გაიზრგება. p-არეში ხვრელები და n-არეში ელექტრონები n–p-გადასასვლელის საწინააღმდეგოდ გადაინაცვლებენ, რითაც ჩამკეტ ფენაში არაძირითადი მატარებლების კონცენტრაციას გაზრდიან. n–p-გადასასვლელში დენი პრაქტიკულად არ გადის. ასეთ შემთხვევაში n–p-გადასასვლელზე მიწოდებულ ძაბვას შებრუნებულს უწოდებენ. ძალიან უმნიშვნელო შებრუნებული დენი გამოწვეულია ნახევარგამტარული მასალის საკუთარი გამტარობით, ე.ი. თავისუფალი ელექტრონების უმნიშვნელო რაოდენობით p-არეში და ხვრელების n-არეში.
თუ n–p-გადასასვლელს წყაროსთან ისე ჩავრათავთ, რომ წყაროს დადებითი პოლუსი მიეთებულია p- არეს, ხოლო უარყოფითი n-არეს, მაშინ ჩამკეტ ფენაში ველის დაძაბულობა შემცირდება, რაც ძირითადი მატარებლების კონტაქტის ფენაში გავლას აადვილებს. ხვრელები p-არეში და ელექტრონები n-არეში, იმოძრავებენ რა ერთმანეთის შემხვედრი მიმართულებით, გადაკვეთენ n–p-გადასასვლელს და შექმნიან პირდაპირი მიმართულების დენს.
n–p-გადასასვლის თვისებას, დენი პრაქტიკულად მხოლოდ ერთი მიმართულებით გაატაროს იყენებენ ხელსაწყოებში, რომლებსაც ნახევარგამტარულ დიოდებს უწოდებენ. ნახევარგამტარულ დიოდებს სილიციუმის ამ გერმანიუმის კრისტალებისაგან ამზადებენ. მათი დამზადებისას რაიმე გამტარობის ტიპის კრისტალში შეაქვთ სხვა ტიპის გამტარობის მინარევი.
ნახევარგამტარული დიოდები გამოიყენება ცვლადი დენის მუდმივად გარდასქმნელ ხელსაწყოებში. სილიციუმის დიოდის ტიპური ვოლტ-ამპერული მახასიათებელი ნახ. 2-ზეა მოყვანილი.
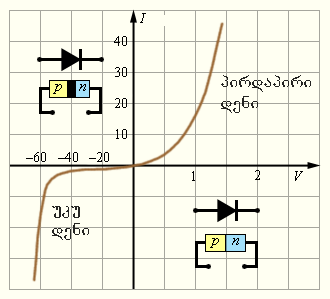
ნახ. 2.
სილიციუმის დიოდის ვოლტ-ამპერული მახასიათებელი. გრაფიკაზე დადებითი და უარყოფითი ძაბვებისთვის სხვადასხვა შკალებია გამოყევებული
ნახევარგამტარულ დიოდებს მრავალი უპირატესობა აქვთ ვაკუუმურთან შედარებით: მცირე ზომები, მოხმარების ხანგრძლივობა, მექანიკური სიმტკიცე. ნახევარგამტარული დიოდების არსებითი ნაკლია მათი მახასიათებლების ტემპერატურაზე დამოკიდებულება. სილიციუმის დიოდებს, მაგალითად, დამაკმაყოფილებლად მუშაობა შეუძლეათ, მხოლოდ –70 °C-დან 80 °C-მდე ტემპერატურულ დიაპაზონში. გერმანიუმის დიოდებისათვის ტემპერატურის მუშა დიაპაზონი უფრო მეტია.
ნახევარგამტარულ ხელსაწყოებს არა ერთი, არამედ ორი n–p-გადასვლით ტრანზისტორებს უწოდებენ. სახელწოდება ორი ინგლისური სიტყვისაგან transfer – გადატან და resistor – წინაარმდეგობა წარმოდგება. ტრანზისტორის შესაქმნელად, ჩვეულებრივ, გერმანიუმი და სილიციუმი გამოიყენაბა. ტრანზისტორები ორი ტიპის არიან: p–n–p-ტრანზისტორები და n–p–n-ტრანზისტორები. მაგალითად, p–n–p-ტიპის გერმანიუმის ტრანზისტორი დონორული მინარევის შემცველ გერმანიუმის მცირე ზომის ფირფიტას წარმოადგენს, ე.ი. n-ტიპის ნახევარგამტარს. ამ შირფიტაში იქმნება აქცეპტურული მინარევის ორი არე, ე.ი. ხვრელური გამტარობის არეები. (ნახ. 3). n–p–n-ტიპის ტრანზისტორში გერმანიუმის ძირითად ფირფიტას p-ტიპის გამტარობა ახასიატებს, ხოლო მასზე შექმნილ ორ არეს - n-ტიპის გამტარობა (Nახ. 4).
ტრანზისტორის ფირფიტას ბაზას უწოდებენ (ბ), საწინაარმდეგი ტიპის ერთ-ერთ არეს - კოლექტორს (კ), მეორეს კი - ემიტერომს (ე). ჩვეულებრივ კოლექტორის მოცულობა ემიტერის მოცულობას აჭარბებს. სქემაზე პირობით აღნიშვნებში ემიტერის ისარი ტრანზისტორში დენის მიმართულებას მიუთითებს.
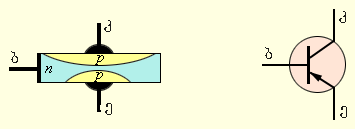
ნახ. 3.
p–n–p სტრუქტურის ტრანზისტორი

ნახ. 4.
n–p–n სტრუქტურის ტრანზისტორი
ტრანზისტორის ორივე n–p-გადასვლა დენის ორი წყაროთია დაკავშირებული. ნახ. 5-ზე p–n–p სტრუქტურის ტრანზისტორის წრედში ჩართვაა ნაჩვენები. „ემიტერ-ბაზა“ გადასვლა პიდაპირი (გამტარებელი) მიმარლებით (ემიტერის წრედი) ირთვება, ხოლო „კოლექტორ-ბაზა“ გადასვლა ჩამკეტი მიმართულებით (კოლექტორის წრედი).
სანამ ემიტერის წრედი ჩაკეტილია, კოლექტრორის წრედში დენი ძალიან მცირეა, რადგანაც თავისუფალი მუხტის მატარებლების -ელექტრონებისათვის ბაზაში და ხვრელებისათვის კოლექტორში - გასასვლელი დაკეტილია.
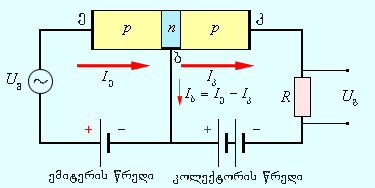
ნახ. 5.
p–n–p ტრანზისტორის ჩართული წრედი
ემიტერის ჩაკეტილი წრედისთვის ხვრელები - ემიტერში მუხტის ძირითადი მატარებლები - ემიტერიდან ბაზაში გადადიან და ქმნიან ამ წრედში Iე დენს. მაგრამ ემიტერიდან ბაზაში მოხვედრილი ხვრელებისთვის კოლექტრორში n–p-გადასვლა ღიაა. ხვრელების დიდ რიცხვი ამ გადასვლების ველის მიერ მიიტაცება და კოლექტორში აღწევს, ქმნის რა მასში Iკ დენს. იმისთვის, რომ კოლექტორის დენი პრაქტიკულად ემიტერის დენის ტოლი იყოს, ტრანზისტორის ბაზას ძალიან თხელი ფირფიტის სახეს აძლევენ. ემიტერში წრედში დენის ცვლილებისას იცველება დენის ძალა კოლექტორშიც.
თუ ემიტერის წრედში ცვლადი ძაბვის წყაროა ჩართული (ნახ. 5), კოლექტორის წრედში ჩართულ R რეზისტორზე, აგრეთვე ცვლადი ძაბვა აღიძვრება, რომლის ამპლიტუდა შეიძლება ბევრჯერ აჭარბებდეს შემავალი სიგნალის ამპლიტუდას. ე.ი. ტრანზისტორი ცვლადი დენის გამაძლიერებლის როლს ასრულებს.
მაგრამ გამაძლიერებლის ასეთი ტარნზისტორული სქემა არ არის ეფექტური, რადგან მასში არ ხდება სიგნალის გაძლიერება დენის მხრივ, და შემავალი სიგნალის წყაროში ემიტერის მთელი Iე დენი გადის. ტრანზისტორული გამაძლიერებლების რეალურ სქემებში ცვლადი ძაბვის წყარო ისე ირთვება, რომ მასში გადის დენის მხოლოდ მცირე ნაწილი გადის Iბ = Iე – Iკ. ბაზის დენის მცირე ცვლილება კოლექტორის დენის მნიშვნელოვან ცვლილებას იწვევს. დენის ასეთ სქემებში შეიძლება რამოდენიმე ასეულჯერ გაძლიერდეს.
დღეისთვის ნახევარგამტარულ ხელსაწყოებს ძალიან ფართო გამოყენება აქვთ რადიოტექნიკაში. თანამედროვე ტექნოლოგიები ისეთი ნახევარგამტარული ხელსაწყოების წარმოების საშუალებას იძლევიან, როგორებიცაა - დიოდები, ტრანზისტორები, ნახევარგამტარული ფოტომიმღებები და ა.შ. - რომელთა ზომები მხოლოდ რამოდენიმე მიკრონია. თვისობრივად ახალი ეტაპი ელექტრონული ტექნიკის განვითარებაში მიკროელექტრონიკის განვითარებით დაიწყო, რომელიც ინტეგრალური მიკროსქემებისა და მათი გამოყენების პრინციპებს ამუშავებს.
ინტეგრალური მიკროსქემებს უწოდებენ ურთიერთდაკავშირებული ელემენტების დიდ ერთობლიობას - ზეპატარა დიოდებს, ტრანზისტორებს, კონდენსატორებს, დამაკავშირებელ სადენებს, რომლებიც ერთიან ტაქნოლოგიურ პროცესში ერთ კრისტალზეა განთავსეული. 1 სმ2 ფართობის მიკროსქმა შეიძლება რამოდენიმე ასეულ ათას მიკროელემენტს შეიცავდეს.
მიკროსქემების გამოყენებამ თანაბედროვე ელექტრულ ტექნიკაში რევოლუციური ცვლილება გამოიწვია. ეს განსაკუთრებით ნათლად ელექტრულ გამომთვლელ მანქანებში გამოვლინდა. უზარმაზარი ელექტრულ გამომთვლელ მანქანები, როლებიც ათეულობით ათას ელექტრულ ნათურას შეიცავდა, პერსონალირმა კომპიუტერებმა შეცვალა.
{loadnavigation}
კუთრი ელექტრული წინაღონის მნიშვნელობების მიხედვით ნახევარგამტარები შუალედურ ადგილს იკავებენ კარგ გამტარებსა და დიელექტრიკებს შორის. ნახევარგამტარებს ეკუთვნის მრავალი ქიმიური ელემენტი (გერმანიუმი, სილიციუმი, სელენი, ტელური, დარიშხანი და სხვა), შენადნობების და ქიმიური ნაერთების უზარმაზარი რაოდენობა. ჩვენი გარმომცველი სამყაროს თითქმის ყველა არაორგანული ნივთიერება ნახევარგამტარია. ბუნებაში ყველაზე გავრცელებული ნახევარგამტარი სილიციუმია, რომელის დედამიწის ქერქის 30 % შეადგენს.
ნახევარგანტარებსა და ლითონებს შორის ხარისხიბრივი განსხვავება პირველ რიგში კუთრი წინაღობის ტემპერატურაზე დამოკიდებულებაში ვლინდება (იხ. ნახ. 4). ნახევარგამტარებში ტემპერატურის შემცირებისას წინაღობა პირიქით იზრდება და აბსოლურურ ნულთან ისინი პრაქტუკულად იზოლატორებად იქცევიან (ნახ. 1).

ნახ. 1.
სუფთა ნახევარგამტარის ρ კუთრი წინაღობის T აბსოლუტურ ტემპერატურაზე დამოკიდებულება
ρ (T) დამოკიდებულების ასეთი სვლა უჩვენებს, რომ ნახევარგამტარებში თავისუფალი მუხტის მატარებლების კონცენტრაცია არ არის მუდმივი, არამედ ტემპერატურის ზრდასთან ერთად იზრდება. ნახევარგამტარებში ელექტრული ველის მექანიზმი არ აიხსნება თავისუფალი ელექრონების აირის მოდელით. განვიხილოთ ეს მექანიძმი გერმანიუნის (Ge) მაგალითზე. სილიციუმის (Si) კრისტალშიც ანალოგიური მექანიზმია.
გერმანიუმის ატომს გარე შრეზე ოთხი სუსტ ბმაში მყოფი ელექტრონი აქვს. მათ ვალენტურ ელექტრონებს უწოდებენ. კრისტალურ მესერში ყოველი ატომი გარშემორტყმულია ოთხი უახლოესი მეზობლით. გერმანიუმის კრისტალში ატომებს შორის კავშირი კოვალენტურია, ე.ი. ხორციელდება ვალენტური ელექტრონების წყვილებით. ყოველი ვალენტური ელექტრონი ორ ატომს ეკუთვნის (ნახ. 2). გერმანიუმის კრისტალში ვალენტური ელექტრონები ატომთან უფრო ძლიერადაა დაკავშირებული, ვიდრე მეტალებში; ამიტომაც გამტარობის ელექტრონების კონცენტრაცია ნახევარგამტარებში ოთახის ტემპერატურაზე მრავალი რიგით ნაკლებია მეტალებთან შედარებით, აბსოლუტური ნულის მახლობლად გერმანიუმის კრისტალში ყველა ელექრონი კავშირების შექმნითაა დაკავებული. ასეთი კრისტალი ელექტრულ დენს არ ატარებს.

ნახ. 2.
წყვილური- ელექტრონული კავშირი გერმანიუმის კრისტალში და ელექტრონულ-ხვრელური წყვილის წარმოქმნა
ტემპერატურის გაზრდისას ვალენტური ელექტრონების გარკვეული ნაწილი მიიღებს კოვალენტური კავშირის გასაწყვეტად საკმარის ენერგიას. მაშინ კრისტალში წარმოიქმნება თავისუფალი ელექტრონები (გამტარობის ელექტრონები). ამავე დროს კავშირის წყვეტის ადგილებში იქმნება ვაკანსია, რომელიც არ არის დაკავებული ელექტრონით. ამ ვაკანსიებმა (თავისუფალმა ადგილებმა) მიიღეს ხვრელის სახელწოდება. ვაკანტური ადგილი შეიძლება სწრაფად იქნეს დაკავებული მეზობელი წყვილის ელექტრონის მიერ, მაშინ ხვრელი კრისტაში ახალ ადგილზე გადაინაცვლებს. ნახევარგამტარის გარკვეულ ტემპერატურაზე დროის ერთეულში წარმოიქმნება ელექტრონულ-ხვრელური წყვილების გარკვეული რაოდენობა. ამავე დროს მიმდინარეობს შებრუნებული პროცესი - თავისუფალი ელექტრონის ხვრელთან შეხვედრისას, ხდება გერმანიუმის ატომებს შორის კავშირის აღდგენა. ამ პროცესს რეკომბიბაცია ეწოდება. ელექტრონულ-ხვრელური წყვილები შეიძლება იბადებიდნენ ასევე ნახევარგამტარის განათებით, ელექტრომაგნიტური გამოსხივების ხარჯზე. ელექტრული ველის არ არსებიბის შემთხვევაში გამტარობის ელექტრონები და ხვრელები ქაოსურ სითბურ მოძრაობაში მონაწილეობენ.
თუ ნახევარგამტარს ელექტრულ ველში მოვათავსებთ, მოწესრიგებულ მოძრაობაში ჩართული აღმოჩნდებიან არა მხოლოდ თავისუფალი ელექტრონები, არამედ ხვრელებიც, რომლებიც დადებითად დამუხტული ნაწილაკების მსგავსად იქცევიან. ამიტომ ნახევარგამტარში I დენი მიიღება In ელექტრონული და Ip ხვრელური დენების შეჯამებით:
I = In + Ip.
ნახევარგამტარში გამტარობის ელექტრონების კონცენტრაცია ხვრელების კონცენტრაციის ტოლია: nn = np. გამტარობის ელექტრონულ-ხვრელური მექანიზმი თავს იჩენს მხოლოდ სუფთა (ე.ი. მინარევების გარეშე) ნახევარგამტარებში. იგი ნახევარგამტარების თავისუფალ ელექტრულ გამტარობად იწოდება.
მინარევების არსებობის შემთხვევაში ელექტრული გამტარობა ძლიერ იცვლება. მაგალითად, სილიციუმის კრისტალში ფოსფორის 0,001 ატომური პროცენტის დამატებისას კუთრი წინაღობა ხუთ რიგზე მეტით მცირდება. მინარევების ასეთი ძლიერი ზეგავლევა შეიძლება ნახევარგამტარების ზემოთ მოცემული აგებულებით აიხსნას.
ნახევარგამტარის კუთრი წინაღობის მკვეთრი შემცირების აუცილებელ პირობას, მასში მინარევების შეტანისას, მინარევის ატომების ვალენტობის კრისტალის ძირითადი ატომების ვალენტობისაგან განსხვავებაა.
მინარევების არსებობის შემთხვევასი ნახევარგამტარების გამტარობას მინარევებიან გამტარობას უწოდებენ. ასხვავებენ ორი სახის მინარევებიან გამტარობას ელექტრონულს და ხვრელურს.
ელექტრონულ გამრატობას ადგილი აქვს, როცა ოთხვალენტიან ატომიანი გერმანიუმის კრისტალში შეყვანილია ხუთვალენტიან ატომი (მაგ. დარიშხანის ატომი, As)
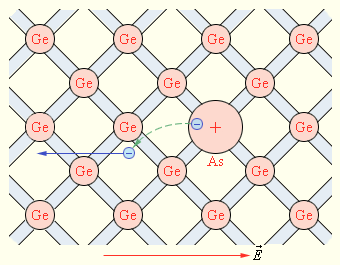
ნახ. 3.
დარიშხანის ატომი გერმანიუმუს მესერში. n-ტიპის ნახევარგამტარი
ნახ. 3-ზე ნაჩვენებია ხუთვალენტიანი დარიშხანის ატომი, რომელიც გერმანიუმის კრისტალის მესერში აღმოჩნდა. დარიშხანის ოთხი ვალენტური ელექტრონი ჩართულია გერმანიუმის ატომებთან კოვალენტური კავშირის დამყარებაში. მეხუთე ვალენტური ელექტრონი ზედმეტი აღმოჩნდა; ის ადვილად წყდება დარიშხანის ატომს და ხდება თავისუფალი. ატომი, რომელმაც ელექტრონი დაკარგა, კრისტალური მესერის კვანძში მოთავსებულ დადებით იონად გადაიქცევა. მინარვს, რომელიც ვალენტობა ნახევარგამტარული კრისტალის ძირითადი ატომების ვალენტობას აჭარბებს, დონორულ მინარევს უწოდებენ. მისი შეყვანის შედეგად კრისტალში ჩნდება თავისუფალი ელექტრონების ნმიშვნელოვანი რაოდენობა. ამის გამო ხდება ნახევაგამტარის კუთრი წინაღობის მკვეთრი შემცირაბა - ათასობით და მილოონობით ჯერადაც კი. მინარევის დიდი შემცველობის ნახევარგამტარის კუთრი წინაღობა შეიძლება მიუახლოვდეს მეტალის გამტარის კუთრ წინაღობას.
დარიშხანის მინარევიან გერმანიუმის კრისტალში არის ელექტრონებიც და ხვრელებიც, როლებიც კრისტალის საკუთრ გამტარობაზე აგებენ პასუხს. მაგრამ თავისუფალი მუხტის ძირითად მატარებელს ელექტრონები წარმოადგენენ. ასეთ კრიტალში nn >> np. ასეთ გამტარობას ელექტრონულს უწოდებენ, ხოლო ნახევარგამტარს, რომელსაც ელექტრონული გამტარობა ახასიათენს n -ტიპოს ნახევარგამტარს.
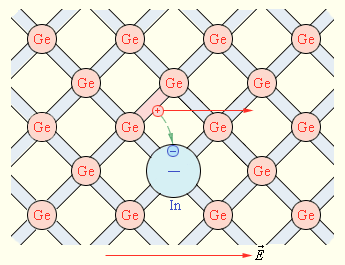
ნახ. 4.
ინდიუმის ატომი გერმანიუმის მესერში. p-ტიპის ნახევარგამტარი
ხვრელური გამტარობა წარმოიშვება, როცა გერმანიმის კრისტალში შეჰყავთ სამვალენტიანი ატომი (მაგ., ინდიუმუს ატომი, In).
ნახ. 4-ზე ნაჩვენებია ინდიუმის ატომი, რომელიც თავისი ვალენტური ელექტრონების საშუალებით ამყარებს კოვალენტურ კავშირს გერმანიუმის მხოლოდ სამ მეზობელ ატომთან. გერმანიუმის მეოთხე ატომთან კავშირის დასამყარებლად ინდიუმს არ აქვს ელექტრონი. ელექტრონის ეს დანაკლისი ინდიუმის ატომმა შეიძლება შეივსოს გერმანიუმის მეზობელი ატომების კოვალენტური კავშირიდან მიტაცებით. ასეთ შემთხვევაში ინდიუმის ატომი კრისტალური მესერის კვანძში განთავსებულ უარყოფით იონად გადაიქცევა, მეზობელი ატომების კოვალენტურ კავშირში კი წარმოიქმნება ვაკანსია. მინარევს, რომლის ატომებსაც შეუძლიათ მიიტაცინ ელექტრონი აქცეპტორულ მინარევებს უწოდებენ. აქცეპტორული მინარევის შეყვანით კრისტაში ირღვევა მრავალი კოვალენტური კავშირი და წარმოიქმნება თავისუფალი ადგილი (ხვრელი). ამ ადგილებზე შეიძლება გადახტნენ ელექტრონები მეზობელი კოვალენტური კავშირებიდან, რაც კრისტალში ხვრელების ქაოსურ ხეტიალს იწვევს.
აქცეპტორული მინარევის არსებობა, თავისუფალი ხვრელების არსებობის ხარჯზე, მკვეთრად ამცირებს ნახევარგამტარის კუთრ წინარობას. აქცეპტორული მინარევიან ნახევარგამტარში ხვრელების კონცენტრაცია საგრძნობლად აჭარბებს ნახევარგამტარის საკუთარი ელექტროგამტარობის მექანიზმის ხარჯზე წარმოქმნილი ელექტრონების კონცენტრაციას: np >> nn. ამ ტიპის გამტარობას ხვრელურ გამტარობას უწოდებენ. მინარევიან ნახევარგამტარს, რომელსაც ხვრელური გამტარობა ახასიათებს p-ტიპის ნახევარგანტარს უწოდებენ. p-ტიპის ნახევარგანტარში თავისუფალი მუხტის ძირითად მატარებლებს ხვრელები წარმოადგენენ.
ხაზი უნდა გაესვას, რომ ხვრელური გამტარობა სინამდვილეში გამოწვეულია გერმანიუმის ერთი ატომის ვაკანსიიდან მეორეში კოვალენტურ კავშირის განმახორციელებელი ელექტრონების ესტაფეტური გადაადგილებით.
n- და p-ტიპის ნახევაგამტარებისთვის თავისუფალი მატარებლების კონცენტრაციის მუდმივობის პირობებში, ომის კანონი დენის ძალისა და ძაბვის გარკვეულ ინტერვალებში სრულდება.
{loadnavigation}
ელექტრული დენი მეტალებში - ელექტრული ველის გავლენით ელექტრონების მოწესრიგებული მოძრაობაა. ცდები უჩვენებენ, რომ მეტალის გამტარში დენის გავლისას ნივთიერების გადატანა არ ხდება, ე.ი. მეტალის იონები ელექტრული მუხტის გადატანაში მონაწილეობას არ ღებულობენ.
მეტალებში ელექტრული დენის ელექტრონული ბუნების უფრო დამაჯერებელი დადასტურება ელექტრონების ინერციის ცდებში იქნა მიღებული. ამერიკელმა ფიზიკოსმა ტოლმენმა და შოტლანდიელმა ფიზიკოსმა სტიუარტმა ამ ცდების მეშვეობით საბოლოოდ დაამტკიცეს, რომ მეტალის გამტარებში დენი ელექტრონების მოძრაობითაა განპირობებული. ტოლმენისა და სტიუარტის ცდების სქემა ნახ. 1-ზეა მოცემული. წვრილი მავთულისაგან დამზადებული ხვიების დიდი რიცხვის მქონე კოჭას სწრაფად აბრუნებდნენ თავის ღერძის გარშემო. კოჭას ბოლოები მოქნილი გამტარების საშუალებით მიერთებული იყო მგრძნობიარე ბალისტიკურ გალვანომეტრთან გ. დაბზრიალებულ კოჭას უცებ ამუხრურჭებდნენ და წრედში წამოიქმნებოდა ხანმოკლე დენი. წრედში გამავალი სრული მუხტი გალვანომეტრის ისრის გადახრით იზომებოდა.

ნახ. 1.
ტოლმენისა და სტიუარტის ცდების სქემა
მბრუნავი კოჭას დამუხრუჭებისას, e მუხტის ყოველ მატარებელზე მოქმედებს მამუხრუჭებელი ძალა \(F=m\frac{dv}{dt}\), რომელიც გვერდითი, ე.ი. არაელექტრული წარმოშვების ძალის როლს ასრულებს. ერთეულ მუხტზე პასუხისმგებელი გვერდითი ძალა, განმარტების მიხედვით, გვერდითი ძალების ველის Eგვ დაძაბულობას წარმოადგენს:
Eგვ\(=-\frac{m}{e}\frac{dv}{dt}\)
აქედან გამომდინარე ,კოჭას დამუხრუჭებისას წრედში აღიძვრება \(\varepsilon\) ელექტრომამოძრავებელი ძალა, რომელიც ტოლია
\(\varepsilon =\)Eგვ\(l=\frac{m}{e}\frac{dv}{dt}l\)
სადაც \(l\) – კოჭას მავთულის სიგრძეა. დამუხრუჭების დროის განმავლობაში წრედში გადი \(q\) მუხტი, რომელიც ტოლია
\(q=\int Idt=\frac{1}{R}\int \varepsilon dt=\frac{m}{e}\frac{lv_{0}}{R}\)
აქ \(I\) – კოჭაში დენის მყისიერი მნიშვნელობაა, R – წრედის სრული წინაღობა, \(v_{0}\) – მავთულის საწყისი წრფივი სიჩქარე.
აქედან გამომდინარე, მეტალებში დენის თავისუფალი მატარებლების კუთრი მუხტი e / m ტოლია:
\(\frac{e}{m}=\frac{lv}{Rq}\)
ამ გამოსახულების მარჯვენა მხარეში შემავალი ყველა სიდიდე შეიძლება გაიზომოს. ცდის შედეგებზე დაყრდნობით ტოლმენმა და სტიუარტმა დაადგინეს, რომ მეტალებში მუხტის თავისუფალ მატარებლებს უარყოფითი ნიშანი აქვთ, ხოლო მატარებლის მუხტის ფარდობა მის მასასთან ახლოსაა, სხვა ცდებიდან მიღებულ, ელექტრონის კუთრ მუხტთან. ასე დადგინდა, რომ მეტალებში მუხტის თავისუფალ მატარებლებს ელექტრონები წარმოადგენენ.
თანამედროვე მონაცემების მიხედვით ელექტრონის მუხტის მოდული (ელემენტარული მუხტი) ტოლია
\(e=1,60218\cdot 10^{-19}\)კლ
ხოლო მისი კუთრი მუხტი
\(\frac{e}{m}=1,75882\cdot 10^{11}\)კლ/კგ
მეტალების კარგი ელექტროგამტარებლობა თავისუფალი ელექტრონების დიდი კონცენტრაციით აიხსნება, რომელიც რიგით ერთეულ მოცულობაში ატომების რაოდენობის ტოლია.
ვარაუდი იმისა, რომ მეტალებში ელექტრულ ველზე პასუხისმგებელი ელექტრონები არიან, ტოლმენისა და სტიუარტის ცდებზე გაცილებით ადრე წარმოიშვა. ჯერ კიდევ 1900 წელს გერმანელმა მეცნიერმა პ.დრუდემ მეტალებში თავისუფალი ელექტრონების არსებობის შესახებ არსებული ჰიპოთეზის საფუძველზე შექმნა მეტალების გამტარობის ელექტრონული თეორია. ამ თეორიამ განვითარება ჰოლანდიელი ფიზიკოსის ჰ.ლორენცის შრომებში ჰპოვა და კლასიკური ელექტრონული თეორიის სახელწოდებითაა ცნობილი. ამ თეორიის თანახმად, მეტალებში ელექტრონები იდეალური აირის სადარი ელექტრონული აირის მსგავსად იქცევიან. ელექტრონული აირი ავსებს მეტალის კრისტალური მესერით წარმომქმნილ იონებს შორის სივრცეს (ნახ. 2).

ნახ. 2.
თავისუფალი ელექტრონების აირი მეტალის კრისტალურ მესერში. ნაჩვენებია ერთ-ერთი ელექტრონის ტრაექტორია.
იონებთან ურთიერთქმედების გამო ელექტრონებს მეტალის დატოვება მხოლოს ე.წ. პოტენციური ბარიერის გადალახვის შემთხვევაში შეუძლეა. ამ ბარიერის სიმაღლეს გამოსვლის მუშაობას უწოდებენ. ჩვეულებრივი (ოთახის) ტემპერატურის დროს ელექტრონებს არ ყოფნის ენერგია პოტენციური ბარიერის გადასალახად.
კრისტალურ მესერთან ურთიერთქმედების გამო ელექტრონის გამოსვლის პოტენციური ენერგია გამტარის შიგნით ნაკლებია, ვიდრე ელექტრონის გამტარიდან მოცილების ენერგიაა. გამტარებში ელექტრონები თავისებურ „პოტენციურ ორმოში“ იმოფებიამ, რომლის სიღრმე პოტენციურ ბარიერეად იწოდება.
ისე როგორც მესერის შემადგენელი იონები, ელექტრონებიც მონაწილეობენ სითბურ მოძრაობაში. იონები სითბურ რხევას ასრულებენ წონასწორობის მდებარეობების - კრისტალური მესერის კვანძების მახლობლად. თავისუფალი ელექტრონები მოძრაობენ ქაოსურად და მოძრაობისას მესერის იონებს ეჯახებიან. ასეთი შეჯახებების შედეგად ელექტრონულ აირსა და მესერს შორის თერმოდინამიკური წონასწორობა მყარდება. დრუდე- ლორენცის თეორიის თანახმად, ელექტრონებს ისეთივე სითბური მოძრაობის საშუალო ენერგია აქვთ, როგორის ერთგვაროვან იდეალურ აირს. ეს საშუალებას იძლევა, მოლეკულურ-კინეტიკური თეორიის ფორმულებზე დაყრდნობით, შეფასდეს ელექტრონების სითბური მოძრაობის საშუალო სიჩქარე \(\bar{v}_{T}\) . ოთახის ტემპერატუტისთვის ის დაახლოებით 105 მ/წმ -ს ტოლია.
გარე ელექტრულ ველში შეტანის შემთხვევაში მეტალის გამტარში გარდა ელექტრონების სითბური მოძრაობისა აღიძვრება მათი მოწესრიგებული მოძრაობა (დრეიფი), ანუ ელექტრული დენი. დრეიფის საშუალო სიჩქარე \(\bar v\)დ შემდეგი მოსაზრებების საშუალებით შეიძლება შეფასდეს. დროის Δt ინტერვალში გამტარის S განივკვეთში გაივლის \(S\)\(\bar v\)დ\(\Delta t\) მოცულობაში მყოფი ყველა ელექტრონი.
ასეთი ელექტრონების რიცხვი ტოლია \(nS\)\(\bar v\)დ\(\Delta t\), სადაც n – თავისუფალი ელექტრონების საშუალო კონცენტრაციაა, რომელიც დაახლოებით, მეტალის გამტარის მოცულობის ერთეულში ატომების რიცხვის ტოლია. გამტარის კვეთაში Δt დროში გადის \(\Delta q=enS\)\(\bar v\)დ\(\Delta t\) მუხტი. აქდან გამოდის:
\(I=\frac{\Delta q}{\Delta t}==enS\)\(\bar v\)დ
ან
\(\bar v\)დ\(=\frac{I}{enS}\)
ატომების კონცენტრაცია n იმყოფება 1028–1029 მ–3ფარგლებში.
ამ ფორმულით შეფასებისას 1 მმ2 განივკვეთის მეტალირი გამტარისათვის, რომელშიც 10 ა დენი გადის, ელექტრონების მოწესრიგებული მოძრაობის \(\bar v\)დ საშუალო სიჩქარის მნიშვნელობა 0,6–6 მმ/წმ ფარგლებშია. ამგვარად, ელექტრონების მოწესრიგებული მოძრაობის საშუალო სიჩქარე \(\bar v\)დ მრავალი რიგით ნაკლებია მათი სითბური მოძრაობის \(\bar v\)T საშუალი სიჩქარეზე \(\bar v\)დ<<\(\bar v\)T.
ნახ. 3 იძლევა წარმოდგენას კრისტალურ მესერში თავისუფალი ელექტრონების მოძრაობის ხასიათზე.

ნახ. 3.
კრისტალურ მესერში თავისუფალი ელექტრონების მოძრაობა: а - მეტალის კრისტალურ მესერში ელექტრონების ქაოსური მოძრაობა; b - ქაოსური მოძრაობა ელექტრული ველით გამოწვეულ დრეიფთან ერთად. დრეიფის მასშტაბი \(\bar v\)დ\(\Delta t\) ძლიერაა გაზრდილი.
დრეიფის მცირე სიჩქარე არ ეწინააღმდეგება ცდით დადგენილ ფაქტს, რომ მუდმივი დენის მთელ წრედში დენი პრაქტიკულად მყისიერად აღიძვრება. წრედის ჩაკეტვა (ჩართვა) იწვევს ელექტროლი ველის გავრცელებას c = 3·108 მ/წმ სიჩქარით. l / c (l – წრედის სიგრძე) რიგის დროში მყარდება ელექტრული ველის სტაციუნარული განაწილება და მასში იწყება ელექტრონების მოწესრიგებული მოძრაობა.
მეტალების კლასიკურ ელექტრონულ თეორიაში ივარაუდება, რომ ელექტრონების მოძრაობა ემორჩილება ნიუტონის მექანიკას. ამ თეორიაში უგულვებელყოფილია ელექტრონებს შორის ურთიერთქმედება, ხოლო დადებით იონებთან ურთიერთქმედება მხოლოდ დაჯახებებამდე დაიყვანება. ივარაუდება აგრეთვე, რომ ყოველი დაჯახებისას ელექტრონი მესერს გადასცემს ელექტრულ ველში დაგროვილ მთელ ენერგიას და ამიტომ დაჯახების შემდეგ იგი იწყებს მოძრაობას დრეიფის ნულოვანი სიჩქარით.
იმისდა მიუხედავად, რომ ყველა ეს დაშვება ძალიან მიახლოებითია, კლასიკური ელექტრონული თეორია არსებითად ხსნის ელექტრული დენის კანონებს მეტალის გამტარში.
ომის კანონი. შეჯახებებს შორის ელექტრონებზე მოქმედებს ძალა, რომელიც მოდულით eE ტოლია, რის შედეგადაც მას ენიჭება აჩქარება \(\frac{e}{m}E\). ამიტომ თავისუფალი განარბენის ბოლოს ელექრტონის დრეიფის სიჩქარე ტოლია
\(v\)დ\(=\)(\(v\)დ)max\(=\frac{e}{mE}\tau\),
სადაც \(\tau\) –თავისუფალი გარბენის დროა, რომელიც გათვლების გასამარტივებლად ყველა ელექტრონისთვის ერთნაერად ითვლება. დრეიფის სიჩქარის საშუალო მნიშვნელობა \(\bar{v}\)დ მაქსიმალური მნიშვნელობის ნახევრის ტოლია:
\(\bar{v}\)დ\(=\)\(\frac{1}2{}\)(\(v\)დ)max\(=\frac{1}{2}\frac{e}{mE}\tau\)
განვიხილოთ \(l\) სიგრძის და S განივკვეთის გამტარი ელექტრონების n კონცენტრაციით. გამტარში გამავალი დენი შეიძლება ჩაიწეროს შემდეგი სახით:
| \(I=enS\bar{v}\)დ\(\frac{1}2\frac{e^{2}\tau nS}{m}E=\frac{e^{2}\tau nS}{2ml}U\) |
სადაც \(U=El\) – ძაბვაა გამტარის ბოლოოებზე. მიღებული ფორმულა მეტალის გამტარისათვის ომის კანონს გამოსახავს. გამტარის ელექტრული წინაღობა ტოლია:
| \(R=\frac{2m}{e^{2}n\tau }\frac{l}{S}\) |
კუთრი წინაღობა ρ და კუთრი გამტარობა ν გამოისახება ფორმულებით:
\(\rho=\frac{2m}{e^{2}n\tau }\); \(\nu =\frac{1}{\rho }=\frac{e^{2}n\tau }{2m}\)
ჯოულ-ლენცის კანონი. ველის მოქმედების შედეგად ელექტრონები თავისუფალი განარბენის ბოლოს იძენენ კინეტიკურ ენერგიას
\(\frac{1}{2}m\)(\(v\)დ)2max\(=\frac{1}{2}\frac{e^{2}x^{2}}{m}E^{2}\)
არსებული ვარაუდების თანახმად მთელი ეს ენერგია დაჯახებისას გადაეცემა მესერს და სითბოდ გადაიქცევა.
Δt დროში ყოველი ელექტრონი განიცდის Δt / τ დაჯახებას. S კვეთისა და l სიგრძის გამტარში nSl ელექტრონია. აქედან გამოდის, რომ Δt დროში გამოყოფილი სითბო ტოლია:
\(\Delta Q=\frac{nSl\Delta t}{\tau }\frac{e^{2}\tau ^{2}}{2m}E^{2}\)\(=\frac{ne^{2}\tau }{2m}\frac{S}{l}U^{2}\Delta t=\frac{U^{2}}{R}\Delta t\)
ეს ფორმულა გამოსახავს ჯოულ-ლენცის კანონს.
ამგვარად, კლასიკური ელექტრონული თეორია ხსნის მეტალებში ელექტრული წინაღობის არსებობას, ომისა და ჯოულ-ლენცის კანონებს. მაგრამ მთელ რიგ საკითხებში კლასიკურ ელექტრონულ თეორიას მივყავართ დასკვნებამდე, როლებიც ცდებს ეწინააღმდეგებიან.
ამ თეორიას არ შეუძლია, მაგალითად, ახსნას, რატომ უდრის მეტალების მოლური თბოტევადობა, ისევე როგორც დიელექტრიკული კრისტალების მოლური სითბოტევადობა 3R-ს, სადაც R - აირის უნივერსალური მუდმივაა. თავისუფალი ელექტრონების არსებობა მეტალების სითბოტევადობაზე გავლენას არ ახდენს.
კლასიკურ ელექტრონულ თეორიას არ შეუძლია ასევე მეტალების კუთრი წინაღობის ტემპერატურაზე დამოკიდებულება ახსნას. თეორია იძლევა დამოკიდებულებას \(\rho =\sqrt{T}\), მაშინ როცა ექსპერიმენტიდან მიიღება \(\rho \sim T\). მაგრამ ყველაზე უფრო ნათელი მაგალითი თეორიასა და ექსპერიმენტს შორის განსვავებისა ზეგამტარობაა.
კლასიკური ელექტრონული თეორიის თანახმად, მეტალების კუთრი წინაღობა გაცივებისას, რჩება რა სასრული სიდიდის, მონოტონურად უნდა კლებულობდეს. ასეთი დამოკიდებულება ექსპერიმენტულად მართლაც დაიკვირვება შედარებით მაღალი ტემპერატურების დროს. უფრო დაბალი, რამოდენიმე კელვინის რიგის, ტემპერატურებისას მრავალი მეტალის კუთრი წინაღობა უკვე აღარაა დამოკიდებული ტემპერატურაზე და აღწევს გარკვეული ზღვრულ მნიშვნელობას.
განსაკუთრებულ ინტერესს იწვევს გასაოცარი მოვლენა, ზეგამტარობა, რომელიც დანიელი ფიზიკოსის ჰ.კამერლინგ-ონეონის მიერ იქნა აღმოჩენილი 1911 წელს. რაღაც გარკვეული ტემპერატურისას Tკრ, რომელის სხვადასხვა ნივთიერებისათვის სხვდასხვაა, კუთრი წინაღობა ნახტომისებურად მცირდება ნულამდე (ნახ. 4). კრიტიკული ტემპერატურა ვერცხლისწყლისთვის ტოლია 4,1 К, ალუმინისთვის 1,2 К, კaლისთვის 3,7 К. ზეგამტარობა დაიკვირვება არ მხოლოდ ელემენტებში, არამედ მრავალ ნაერთსა და შენადნობში. მაგალითად, ნიობის კალასთან (Ni3Sn) შენადნობის კრიტიკული ტემპერატურა 18 К. ზოგი ნივთიერება, რომლებიც დამალ ტემპერატურაზე ზეგამტარობას ამჟღავნებს, არაა გამტარი ჩვეულებრივ ტემპერატურაზე. ამავე დროს, ისეთი „კარგი“ გამტარები, როგორიც სპილენძი და ვერცხლია, დაბალ ტემპერატურაზე ზეგამტარები არ ხდებიან.

ნახ. 4
კუთრი წინაღობის ρ დამოკიდებულება აბსოლუტურ ტემპერატურაზე T დაბალი ტემპერატურების დროს: a - ნორმალური მეტალები; b -ზეგამტარები
ნივთიერებას ზეგამტარ მდგომარეობაში განსაკუთრებული თვისებები აქვთ. პრაქტიკულად, მათ შორის ყველაზე მნიშვნელოვანია, ის რომ მათ შეუძლიათ ხანგრძლივი დროის განმავლობაში (მრავალი წელი) მილევის გარეშე შეინარჩუნონ ზეგამტარ წრედში აღძრული ელექტრული დენი.
კლასიკურ ელექტრონულ თეორიას არ შეუძლია ზეგამტარობის ახსნა. ამ მოვლენის მექანიზმის ახსნა მისი აღმოჩენიდან მხოლოდ 60 წლის შემდეგ მოხერხდა კვანტურ-მექანიკური წარმოდგენების საფუძველზე.
ზეგამტარობისადმი ინტერესი იზრდებოდა მაღალი კრიტიკული ტემპერატურების მქონე ახალი მეტალების რიცხვის ზრდასთან ერთად. მნიშვნელოვანი ნაბიჯი ამ მიმართულებით გადაიდგა 1986 წელს, როცა აღმოჩნდა, რომ ერთი რთული კერამიკული ნაერთის Tკრ = 35 K. უკვე შემდეგ 1987 წელს ფიზიკოსებმა შეძლეს შეექმნათ ახალი კერამიკა კრიტიკული ტემპერატურით 98 К, რომელიც თხევადი აზოტის ტემპერატურას აჭარბებს (77 К). ნივთიერებების გადასვლას ზეგამტარ მდგომარეობაში ტემპერატურებზე, რომელიც თხევადი აზოტის დუღილის ტემპერატურას აჭარბებს, მაღალტემპერატურული ზეგამტარობა ეწოდა. 1988 წელს შეიქმნა კერამიკული ნაერთი Tl–Ca–Ba–Cu–O ელემენტებისაგან, კრიტიკული ტემპერატურით 125 К.
ამჟამად წარმოებს სამუშაოები უფრო მაღალი კრიტიკული ტემპერატურის მქონე ახალი ნივთიერებების მოსაძებნად. მეცნიერები იმედოვნებენ ისეთი ნივთიერების მიღებას, რომელიც ოთახის ტემპერატურაზე იქნება ზეგამტარი. თუ ეს მოხდება, ეს იქნება ნამდვილი რევოლუცია მეცნიერებაში, ტექნიკაში და საერთოდ ადამიანების ცხოვრებაში.
უნდა აღინიშნოს, რომ კერამიკული მასალის მაღალტემპერატურული ზეგამტარობის მექანიზმი ბოლოომდე არ არის ასნილი.
{loadnavigation}
წრედის ერთგვაროვან უბანში დენის გავლისას ელექტრული ველი ასრულებს მუშაობას. \(\Delta t\) დროის განმავლობაში წრედში გაივლის \(\Delta q=I\Delta t\) მუხტი. გომოყოფილ უბანზე დენის ძალა ასრულებს მუშაობას
\(\Delta A=\left ( \varphi _{1}+\varphi _{2} \right )\Delta q=\Delta \varphi _{12}I\Delta t=UI\Delta t\),
სადაც \(U=\Delta \varphi _{12}\) – ძაბვაა. ამ მუშაობას ელექტრული ველის მუშაობას უწოდებენ.
თუ ერთგვაროვანი წრედის \(R\) წინარობის მქონე უბნისათვის ომის კანონის ფორმულის
\(RI=U\)
ორივე ნაწილს გავამრავლებთ \(I\Delta t\), მივიღებთ
\(RI^{2}\Delta t=UI\Delta t=\Delta A\) .
ეს ფორმულა ენერგიის შენახვის კანონს გამოსახავს წრედის ერთგვაროვანი უბნისათვის.
R წინაღობის უძრავ გამტარში გამავალი ელექტრული \(I\) დენის მუშაობა \(\Delta A\) გამტარზე გამოყოფილ \(\Delta Q\) სითბოდ გარდაიქმნება
\(\Delta Q=\Delta A=RI^{2}\Delta t\)
დენის მუშაობის სითბოდ გარდაქმნის კანონი ერთმანეთისგან დამოუკიდებლად ექსპერიმენტულად იქნა დადგენილი ჯ. ჯოულისა და ე. ლენცის მიერ და ჯოულ-ლენცის სახელს ატარებს.
ელექტრული დენის სიმძლავრე ტოლია დენის მუშაობის ფარდობისა დროის იმ ინტერვალთან, რომელშიაც ეს მუშაობა შესრულდა:
\(P=\frac{\Delta A}{\Delta t}=UI=I^{2}R=\frac{U^{2}}{R}\)
სი სისტემაში ელექტრული დენის მუშაობა ჯოულებში (ჯ) გამოისახება, სიმძლავრე კი - ვატებში (ვ).
ახლა განვიხილოთ მუდმივი ძალის სრული წრედი, რომელიც შედგება \(\dpi{150} \varepsilon\) ელექტრომამოძრავებელი ძალის მქონე დენის წყაროსგან, შიგა \(r\) წინაღობისა და \(R\) წინაღობის მქონე გარე ერთგვაროვანი უბნისაგან. სრული წრედისთვის ომის კანონი ჩაიწერება შემდეგი სახით
\(\left ( R+r \right )I=\varepsilon\).
ამ ფორმული ორივე მხარის \(\Delta q=I\Delta t\)-ზე გამრავლებით მივიღებთ მუდმივი დენის სრული წრედისათვის ენერგიის შენახვის გამომსახულებას:
\(RI^{2}\Delta t+rI^{2}\Delta t=\varepsilon I\Delta t=\Delta A\)გარე.
მარცხენა ნაწილის პირველი წევრი \(\Delta Q=RI^{2}\Delta t\) – \(\Delta t\) დროში გარე უბანზე გამოყოფილი სითბოა, მეორე წევრი
\(\Delta Q\)წყარო \(=rI^{2}\Delta t\) – იგივე დროში წყაროს შიგნით გამოყოფილი სითბოა.
გამოსახულება \(\varepsilon I\Delta ტ\) წყაროს შიგნით მომქმედი გვერდითი ძალების \(\Delta A\)გვ მუშაობის ტოლია.
ჩაკეტილ წრედში ელექტრული დენი გავლისას გვერდითი ძალენის მუშაობა \(\Delta A\)გვ გარე წრედში (\(\Delta Q\)) და წყაროს შიგნით (\(\Delta Q\)წყარო) გამოყოფილ სითბოდ გარდაიქმნება.
\(\Delta Q\) + \(\Delta Q\)წყარო = \(\Delta A\)წყარო = \(\varepsilon I\Delta ტ\).
საყურადღებოა, რომ ამ გამოსახულებაში არ შედის ელექტრული ველის მუშაობა. ჩაკეტილ წრედში დენის გავლისას ელექტრული ველი მუშაობას არ ასრულებს; ამიტომ სითბო გამომუშავდება მხოლოდ წყაროს შიგნით მომქმედი გვერდითი ძალების მიერ. ელექტრული ველი მხოლოდ წრედის სხვადასხვა უბნებს შორის სითბოს გადანაწილებას ახდენს.
გარე წრედი შეიძლება წარმოადგენდეს მხოლოდ R წინაღობის გამტარს, არამედ სიმძლავრის მომხმარებელ რაღაც ხელსაწყოსაც, მაგალითად, მუდმივი დების ძრავას. ასეთ შემთხვევაში R-ის ქვეშ დატვირთვის ექვივალენტური წინაღობა იგულისხმება. გარე წრედზე გამოყოფილი ენერგია ნაწილობრივ ან მთლიანად გარდაიქმნება არა მხოლოს სითბოდ, არამე ენერგიის სხვა სახეებად, მაგალითად, ელექტრო ძრავის მიერ შესრულებულ მექანიკურ მუშაობად. ამიტომაც დენის წყაროს ენერგიის გამოყენების საკითხს დიდი პრაქტიკული მნიშვნელიბა ენიჭება.
წყაროს სრული სიმძლავრე, ე.ი. დროის ერთეულში გვერდითი ძალევის მიერ შესრულებული მუშაობა, ტოლია
\(P\)წყ\(=\varepsilon I=\frac{\varepsilon ^{2}}{r+R}\)
გარე წრედში გამოიყოფა სიმძლავრე
\(P=RI^{2}=\varepsilon I-rI^{2}=\frac{\varepsilon ^{2}}{\left ( R+r \right )^{2}}\)
ფარდობას \(\eta =\frac{P}{P_{wy}}\) , რომელიც ტოლია
\(\eta =\frac{P}{P_{wy}}=1-\frac{r}{\varepsilon }I=\frac{R}{R+r}\)
მარგი ქმედების კოეფიციენტი ეწოდება.
ნახ. 1-ზე გრაფიკულადაა გამოსახული წყაროს Pwy სიმძლავრის, გარე წრედზე გამოყოფილი სასარგებლო P სიმძლავრის, და მარგი ქმედების η კოეფიციენტის დამოკიდებულება წრედის \(\dpi{120} \varepsilon\)- ტოლი ემძ-ს მქონე წყაროს I დენსა და შიგა r წინაღობას შორის. წრედში დენი შეიძლება იცვლებოდეს \(I=0\) -დან (როცა \(R=\infty\)) \(I\)=\(I\)მჩ=\(\frac{\varepsilon }{r}\) -მდე (როცა R = 0) საზღვრებში.

ნახ. 1.
წყაროს \(P\)წყარო სიმძლავრის, სასარგებლო \(P\) სიმძლავრის, და წყაროს მარგი ქმედების η კოეფიციენტის დამოკიდებულება
მოყვანილი გრაფიკებიდან ჩანს, რომ გარე წრედის მაქსიმალური სიმძლავრე \(P\)max, რომელიც ტოლია
\(P_{max}=\frac{\varepsilon ^{2}}{4r}\)
მიიღწევა როცა R = r.ამ დროს წრედში დენი ტოლია
\(I_{max}=\frac{1}2{I}\) მჩ\(=\frac{\varepsilon }{2r}\)
ხოლო წყაროს მქკ კი ტოლია 50 %-ს. მქკ-ს მაქსიმალური მნიშვნელობა მიიღწევა როცა I → 0, ე.ი., როცა R →\(\infty\). მოკლე ჩართვისას სასარგებლო სიმძლავრე P = 0 და მთელი სიმძლავრე გამოიოფა წყაროა შიგნით, რასაც მისი გადახურება და გარღვევა შეუძლია გამოიწვიოს. წყაროს მქკ ამ დროს ნულის ტოლია.
