{loadnavigation}
წინა თავში მოყვანილია ფორმულები რმლებიც რეზისტორის, კონდენსატორისა და ინდუქციურობის კოჭასათვის ცვლადი დენისა და ძაბვის ამპლიტუდებს შორის კავშირს იძლევა:
 (*)
(*)
ეს ფორმულები გარეგნულად მუდმივი დენის წრედის უბნისთვის ომის კანონს მოგვაგონებს, მაგრამ ახლა მასში შედიან არა წრედის უბნის მუდმივი დენისა და ძაბვის მნიშვნელობები, არამედ ცვლადი დენისა და ძაბვის ამპლიტუდების მნიშვნელობები.
(*) ფორმულები გამოსახავენ ომის კანონს ცვლადი დენის წრეისათვის, რომელიც R, L და C ელემენტებიდან ერთ-ერთს შეიცავს. ფიზიკურ სიდიდეებს R,  და ωL რეზისტორის აქტიური წინაღობა, კონდენსატორის ტევადობითი წინაღობა და კოჭას ინდუქციური წინაღობა ეწოდებათ.
და ωL რეზისტორის აქტიური წინაღობა, კონდენსატორის ტევადობითი წინაღობა და კოჭას ინდუქციური წინაღობა ეწოდებათ.
წრედის უბანში ცვლადი დენის გავლისას ელექტრომაგნიტური ველი ასრულებს მუშაობას და წრედში ჯოულის სითბო გამოიოფა. ცვლადი დენის წრედის მეყსეული სიმძლავრე დენის და ძაბვის მეყსეულ მნიშვნელობათა ნამრავლის ტოლია: p = J · u. პრაქტიკულ ინტერესს ცვლადი დენის პერიოდის განმავლობაში სიმძლავრის საშუალო მნიშვნელობა იწვევს

აქ I0 და U0 – წრედის მოცემულ უბანზე დენისა და ძაბვის ამპლიტუდათა მნიშვნელობებია, φ – დენსა და ძიბვას შორის ფაზათა წანაცვლება. ხაზი საშუალო მნიშვნელობას ნიშნავს. თუ წრედის უბანი მხოლოს R წინარობის რეზისტორს შეიცავს, მაშინ ფაზათა წანაცვლება φ = 0:

იმისათვის, რომ ეს გამოსახულება გარეგნულად ემთხვეოდეს მუდმივი დენისთვის სიმძლავრის ფორმულას, შემოაქვთ დენის ძალისა და ძაბვის მომქმედი ან ეფექრური მნიშვნელობის ცნება:
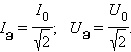
რეზისტორის შემცველი წრედის უბნის სიმძლავრე ცვლადი დენისთვის ტოლია
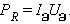
თუ წრედის უბანი შეიცავს მხოლოდ C ტევადობის კონდენსატორს, მაშინ ფაზის წანაცვლება დენსა და ძაბბას შორის  . ამიტომ
. ამიტომ
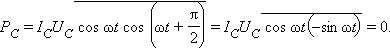
ანალოგიურად შეიძლება ვუჩვენოთ, რომ PL = 0.
ამგვარად, ცვლადი დენის წრედის სიმძლავრე მხოლოს აქტიურ წინაღობაზე გამოიყოფა. კონდენსატორზე და ინდუქციურობის კოჭაზე ცვლადი დენის საშუალო სიმძლავრე ნულის ტოლია.
ახლა განვიხილოთ ელექტრული წრედი, რომელიც მიმდევრიბით შეერთებული რაზისტორის, კონდენსატორისა და კოჭასაგან შედგება. წრედი ω სიხშირის ცვლადი დენის წყაროსთანაა მიერთებული. წრედის ყველა მიმდევრობით შეერთებულ უბანზე ერთნაერი დენი გადის. გარე წყაროს ძაბვასა e (t) და დენს J (t) შორის წარმოიშვება რაღაც φ კუთხის ტოლი ფაზის წანაცვლება. ამიტომ შეიძლება დაიწერის
J (t) = I0 cos ωt; e (t) =  0 cos (ωt + φ).
0 cos (ωt + φ).
დენისა და ძაბვის მაყსეულ მნიშვნელობათა ასეთი ჩანაწერი ვექტორულ დიაგრამას (ნახ. 2) შეესაბამება. ცვლადი დენის მიერ განვითარებული საშუალო სიმძლავრე ტოლია

როგირც ვექტორული დიაგრამიდავ ჩანს, UR =  0 · cos φ, ამიტომ
0 · cos φ, ამიტომ  . აქედან გამომდინარე, წაყროს მთელი სიმძლავრე რეზისტორზე ჯოულის სითბოს სახით გამოიყოფა, რაც ზემოთ გაკეთებულ დასკვნას ამტკიცებს.
. აქედან გამომდინარე, წაყროს მთელი სიმძლავრე რეზისტორზე ჯოულის სითბოს სახით გამოიყოფა, რაც ზემოთ გაკეთებულ დასკვნას ამტკიცებს.
წინა თავში მოყვანილი იყო RLC-წრედში დენისა I0 და ძაბვის  0 ამპლიტუდებს შორის დამოკიდებულება:
0 ამპლიტუდებს შორის დამოკიდებულება:

სიდიდეს
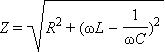
ცვლადი დენის წრედის სრულ წინაღობას უწოდებენ. დენისა და ძაბვის ამპლიტუდებს შორის დამოკიდებულების გამომსახველი ფორმულა შეიძლება ჩაიწეროს შემდეგი სახით
ZI0 =  0. (**)
0. (**)
ამ თანაფარდობას უწოდებენ ომის კანონს ცვლადი დენის წრედისათბის. ამ პარაგრაფის დასაწყისში მოყვანილი (*) ფორმულა, გამოსახავს (**) ომის კანონის კერძო სახეს.
სრული წინაღობის ცნება ცვლადი დენიდ წრედის გათვლისას მნიშვნელოვან როლს ასრულებს. წრედის სრული წინაღობის განსაზღვრისათვის ბევრ შემთხვევაში მოსახერხებელია ვექტორული დიაგრამის მეთოდის გამოყენება. მაგალითისთვის განვიხილოთ პარალელური RLC-კონტური, რომელიც ცვლადი დენის გარე წყარისთანაა მიერთებული (ნახ. 1).

ნახ. 1.
პარალელური RLC-კონტური
ვექტორული დიაგრამის აგებისას უნდა გავითვალისწინოთ, რომ პარალელური შეერთებისას ყველა R, C და L ელემენტში ძაბვა ერთნაერია და გარე წყაროს ძაბვის ტოლია. წრედის სხვადასხვა შტოში გამავალი დენები გამსხვავდებიან არა მარტო ამპლიტუდების მნიშვნელობებით, არამედ მოდებული ძაბვის მიმართ ფაზის წანაცვლებითაც. ამიტონ წრედის სრული წინაღობა არ შეიძლება გამოითვალოს პარალელური წრედის კანონების მიხედვით. პარალელური RLC-კონტურის ვექტორული დიაგრამა ნახ. 2-ზეა გამოსახული.
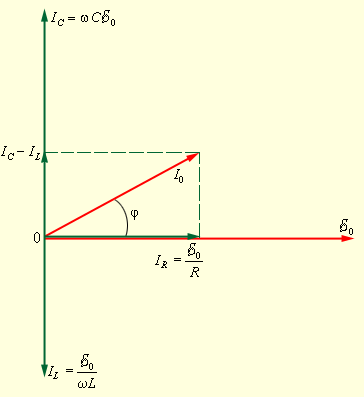
ნახ. 2.
პარალელური RLC-კონტურის ვექტორული დიაგრამა
დიაგრამიდან გამოდის:

ამიტომ პარალელური RLC-კონტურის სრული წინაღობა გამოისახება თანაფარდობით
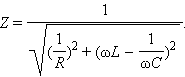
პარალელური რეზონანსისას (ω2 = 1 / LC) სრული წინაღობის მაქსიმალურ მნიშვნელობა რეზისტორის აქტიური წინაღობის ტოლია:
Z = Zmax = R.
დენს და ძაბვას შორის ფაზის წანაცვლება φ პარალელური რეზონანსისას ნულის ტოლია.
{loadnavigation}
გარე პერიოდული დენის წყაროს მოქმედებით ელექტრულ წრედში აღძრულ პროცესებს იძულებით რხევებს უწოდებენ.
იძულებითი რხევები, წრედში საკუთარი რხევებისაგან განსხვავებით, მიულევადია. პერიოდული ზემოქმედების გარე წყარო სისტემასთან ენერგიის მოდინებას უზრუნველყოფს და გარდაუვალი დანაკარგების მიუხედავად, რხევებს მილევის საშუალებას არ აძლევს.
განსაკუთრებულ ინტერესს იწვევს შემთხვევა, როცა გარე წყარო, რომლის ძაბვა ω სიხშირით, ჰარმონიული კანონით იცველბა, ჩართულია ელექტრულ წრედში, რომელსაც გარკვეული ω0 სიხშირის საკუთარი თავისუფალი რხევების შესრულება შეუძლია.
თუ თავისუფალი ω0 რხევის სიხშირე ელექტრული წრედის პარამეტრებით განისაზღვრება, მაშინ დამყარებული იძულებითი რხევები გარე წყაროს ω სიხშირით მიმდინარეობს.
წრედში გარე წყაროს ჩართვის შემდეგ სტაციონალური იძულებითი რხევების დასამყარებლად აუცილებელია გარკვეული Δt დრო. ეს დრო რიგით წრედში თავისუფალი რხევების მილევის τ დროის ტოლია.
ელექტრულ წრედებს, რომლებშიც დენის პერიოდული წყარის მოქმედებით დამყარებული იძულებითი რხევები მიმდინარეობს, ცვალდი დენის წრედებს უწოდებენ.
განვიხილოთ მიმდევრობითი რხევითი კონტური, ანუ RLC-წრედი, როლელშიც ჩართული დენის წყაროს ძაბვა პერიოდული კანონით იცვლება (ნახ.1):
|
e (t) = |
სადაც  0 – ამპლიტუდაა, ω – წრიული სიხშირე.
0 – ამპლიტუდაა, ω – წრიული სიხშირე.

ნახ. 1.
იძულებითი რხევები კონტურში
იგულისხმება, რომ ნახ. 1-ზე გამოსახულ ელექტრულ წრედში სრულდება კვაზისტაციონარობის პირობა. ამიტომ დენისა და ძაბვის მეყსეილი მნიშვნელობებისთვის ომის კანონი შეიძლება ჩაიწეროს ასე:

სიდიდე  - კოჭას თვითინდუქციის ემძ-ა, რომელიც განტოლების მარჯვენა მხარიდან, ნიშნის შეცვლით, მარცხნივაა გადატანილი. ამ სიდიდეს ინდუქტიურობის კოჭას დაძაბულობას უწოდებენ.
- კოჭას თვითინდუქციის ემძ-ა, რომელიც განტოლების მარჯვენა მხარიდან, ნიშნის შეცვლით, მარცხნივაა გადატანილი. ამ სიდიდეს ინდუქტიურობის კოჭას დაძაბულობას უწოდებენ.
იძულებოთი რხევების განტოლება შეიძლება ჩაიწეროს შემდეგი სახით
uR + uC + uL = e (t) =  0 cos ωt,
0 cos ωt,
სადაც uR (t), uC (t) და uL (t) – ძაბვებია რეზისტორზე, კონდენსატორსა და კოჭაზე შესაბამისად. ამ ძაბვების ამპლიტუდები ავღნიშნოთ UR, UC და UL-თი. იძულებითი რხევების დამყარების შემდეგ ყველა ძაბვა ცვლადი დენის გარე წყაროს ω სიხშირით იცვლება. იძულებოთი რხევების განტოლების ამოხსნის ვიზუალიზაციისათვის შეიძლება ვექტორული დიაგრამების მეთოდის გამოყენება.
ვექტორულ დიაგრამაზე გარკვეილი წინასწარ განსაზრვრული ω სიხშირის რხევები ვექტორების სახით გამოისახება (ნახ. 2).

ნახ. 2.
ჰარმონიული A cos (ωt + φ1),B cos (ωt + φ2) რხევების და მათი ჯამის C cos (ωt + φ) ვექტორული გამოსახვა ვექტორულ დიაგრამაზე
დიაგრამაზე ვექტორების სიგრძეები A და B რხევების ამპლიტუდების ტოლია, ჰორიზონტული ღერძის მიმართ დახრა კი რხევების φ1 და φ2 ებით განისაზღვრება. ვექტორების ორიენტაცია ურთიერთის მიმართ ფაზათა ფარდობითი წანაცვლებით Δφ = φ1 – φ2 განისაზღვრება. ჯამური რხევის გამომსახველი ვექტორი, ვექტორულ დიაგრამაზე, ვექტორების შეკრების წესით იგება:

იმისათვის, რომ ელექტრულ წრედში იძულებითი რხევებისათვის აიგოს ძაბვებისა და დენების ვექტორული დაიაგრამა, უნდა ვიცოდეთ დენებისა და ძაბვების ამპლიტუდების თანაფარდობა და მათ შორის ფაზათა სხვაობა წრედის ყველა უბნისთვის.
ცალცალკე განვიხილოთ ცვლადი დენის გარე წყაროს ჩართვა R წინაღობის რეზისტორთან, C ტევადობის კონდენსატორთან და L ინდუქტიურობის კოჭასთან. სამივე შემთხვევაში ძაბვა რეზისტორზე, კონდენსატორზე და კოჭაზე ცვლადი დენის წყაროს ძაბვის ტოლია.
1. რეზისტორი ცვლადი დენის წრედში

აქ IR-ით რეზისტორში გამავალი დენის ამპლიტუდაა აღნიშნული. რეზისტორში დენისა და ძაბვის ამპლიტუდებს შორის კავშირი გამოისახება თანაფარდობით
RIR = UR.
რეზისტორზე დენისა და ძაბვის ფაზათა წანაცვლება ნულის ტოლია.
ფიზიკურ სიდიდეს R რეზისტორის აქტიურ წინაღობას უწოდებენ.
2. კონდენსატორი р ცვლადი დენის წრედში


დენისა IC და ძაბვის UC ამპლიტუდებს შორის კავშირი გამოისახება თანაფარდობით

დენი ძაბვას უსწრებს ფაზაში  კუთხით.
კუთხით.
ფიზიკურ სიდიდეს  კონდენსატორის ტევადობით წინაღობას უწოდებენ.
კონდენსატორის ტევადობით წინაღობას უწოდებენ.
3. კოჭა ცვლადი დენის წრედში


IL დენისა და UL ძაბვის ამპლიტუდებს შორის კავშირი გამოისახება თანაფარდობით
ω L IL = UL.
დენი ძაბვას ჩამორჩება ფაზაში  კუთხით.
კუთხით.
ფიზიკურ სიდიდეს XL = ωL კოჭას ინდუქციურ წინაღობას უწოდებენ.
ახლა შეიძლება აიგოს ვექტორული დიაგრამა მიმდევრობითი RLC-კონტურისათვის, რომელშიც ω სიხშირის იძულებითი რხევები მიმდინარეობს. რადგანაც წრედის მიმდევრობით მიერთებულ უბნებში გამავალი დენი ერთნაერია, ვექტორული დიაგრამის წრედში დენის რხევის გამომსახველი ვექტორის მიმართ აგებაა მოსახერხებელი. დენის ამპლიტუდა ავღნიშნოთ I0 -ითი. დენის ფაზა ნულის ტოლადაა მიღებული. ეს სრულიად დასაშვებია, რადგან ფიზიკურ ინტერესს წარმოადგენს არა ფაზის აბსოლუტური მნიშვნელობა, არამედ ფაზათა ფარდობითი წანაცვლება. ვექტორული დიაგრამა მიმდევრობითი RLC-წრედისათვის ნახ. 2-ზეა გამოსახული.

ნახ. 3.
მიმდევრობითი RLC-წრედის ვექტორული დიაგრამა
ნახ. 3-ზე ვექტორული დიაგრამა აგებულია შემთხვევისათვის, როცა  ან
ან  . ასეთ შემთხვევაში გარე წყაროს ძაბვა წრედში გამავალ დენს ფაზაში უსწრებს გარკვეული φ კუთხით.
. ასეთ შემთხვევაში გარე წყაროს ძაბვა წრედში გამავალ დენს ფაზაში უსწრებს გარკვეული φ კუთხით.
ნახაზიდან ჩანს, რომ

აქედან გამოდის

I0 გამოსახილებიდან ჩანს, რომ დენის ამპლიტუდა მაქსიმალურ მნიშვნელობას ღებულობს როცა

ან

დენის რხევის ამპლიტუდის ზრდის მოვლენა, გარე წყაროს რხევის ω სიხშირის ელექტრული წრედის საკუთარ ω0 სიხშირესთან დამთხვევის შემთხვევაში ელექტრულ რეზონანსს უწოდებენ. რეზონანსისას

რეზონანსის დროს ფაზათა წანაცვლება მოდებულ ძაბვასა და წრედში გამავალ დენს შორის ნული ტოლი ხდება. მიმდევრობით RLC-წრედში რეზონანსს ძაბვის რეზონანსს უწოდებენ. ანალოგიურად, ვექტორული დიაგრამის საშუალებით შეიძლება რეზონანსის მოვლენის შესწავლა R, L და C ელემენტების პარალელური შეერთების შემტხვევაში (ე.წ. დენების რეზონანსი).
მიმდევრობითი რეზონანსისას (ω = ω0) კონდენსატორისა და კოჭას ძაბვების ამპლიტუდები UC და UL მკვეთრად იზრდება:

წინა თავში შემოტანილი იყო RLC-კონტურის ვარგისიანობის ცნება:

ამგვარად, რეზონანსისას კონდენსატორისა და კოჭას ძაბვების ამპლიტუდები Q-ჯერ აჭარბებს გარე წყაროს ძაბვის ამპლიტუდას.

ნახ. 4.
სხვადასხვა Q ვარგისიანობის კონტურების რეზონანსული მრუდები
ნახ. 4-ზე მიმდევრობითი ელექტრული კონტურების რეზონანსის მოვლენაა წარმოდგენილი. ნახაზზე გრაფიკულადაა გამოსახული კონდენსატორზე ძაბვის UC ამპლიტუდის გარე წყაროს ძაბვის  0 ამპლიტუდასთან ფარდობის დამოკიდებულება მის სიხშირეზე სხვადასხვა Q ვარგისიანობის შემთხვევაში. ნახ. 4-ზე მრუდებს რეზონანსულ მრუდებს უწოდებენ.
0 ამპლიტუდასთან ფარდობის დამოკიდებულება მის სიხშირეზე სხვადასხვა Q ვარგისიანობის შემთხვევაში. ნახ. 4-ზე მრუდებს რეზონანსულ მრუდებს უწოდებენ.
შეიძლება ჩვენება, რომ დაბალი ვარგისიანობის კონტურების რეზონანსული მრუდების მაქსიმუმი ცატათი დაბალი სიხშირეებისკენაა ჩანაცვლებული.
{loadnavigation}
ელექტრულ წრედებში, ისევე როგორც მაქანიკურ სისტემებში, როგორიცაა ტვირთი ზამბარაზე ან ქანქარა, შეიძლება აღიძრას თავისუფალი რხევები. უმარტივესი ელექტრულ სისტემა, რომელსაც თავისუფალი რხევების შესრულება შეუძლია მიმდევრობითი RLC-წრედია (ნახ. 1).

ნახ. 1.
მიმდევრობითი RLC-კონტური
როცა K ჩამრთველი 1 მდებარეობაშია, კონდენსატორი  ძაბვამდე იმუხტება. 2 მდებარეობაში გადართვისას იწყება კონდენსატორის განმუხტვის პროცესი R წინაღობის რეზისტორისა და L ინდუქტიურობის კოჭას საშუალებით. გარკვეულ პირობებში ამ პროცესს შეიძლება რხევითი ხასიათი ჰქონდეს.
ძაბვამდე იმუხტება. 2 მდებარეობაში გადართვისას იწყება კონდენსატორის განმუხტვის პროცესი R წინაღობის რეზისტორისა და L ინდუქტიურობის კოჭას საშუალებით. გარკვეულ პირობებში ამ პროცესს შეიძლება რხევითი ხასიათი ჰქონდეს.
ომის კანონი ჩაკეტილი RLC-წრედისათვის, რომელიც გარე დენის წყაროს არ შეიცავს, ასე ჩაიწერება

სადაც  – კონდენსატორზე მოდებული ძაბვაა, q – კონდენსატორის მუხტი,
– კონდენსატორზე მოდებული ძაბვაა, q – კონდენსატორის მუხტი,  – დენი წრედში. ამ თანაფარდობის მარჯვენა მხარეს გვაქვ კოჭას თვითინდუქციის ემძ. თუ ცვლადი სიდიდეთ კონდენსატორის q (t) მუხტს ავირჩევთ, განტოლება, რომელიც RLC-წრედის თავისუფალი რხევებს აღწერს, შეიძლება მივიყვანოთ სახეზე:
– დენი წრედში. ამ თანაფარდობის მარჯვენა მხარეს გვაქვ კოჭას თვითინდუქციის ემძ. თუ ცვლადი სიდიდეთ კონდენსატორის q (t) მუხტს ავირჩევთ, განტოლება, რომელიც RLC-წრედის თავისუფალი რხევებს აღწერს, შეიძლება მივიყვანოთ სახეზე:

ჯერ განვიხილოთ შემთხვევა, როცა კონტურში არ არის ელექტრომაგნიტური ენერგიის დანაკარგი (R = 0). მაშინ
 (*)
(*)
აქ მიღებულია აღნიშვნა:  (*) განტოლება აღწერს თავისუფალ რხევებს LC-კონტურში, როცა არა არის მილევა. იგი ზუსტად ისევე გამოიყურება როგორც ზამბარაზე დამაგრებული ტვირთის რხევის განტოლება ხახუნის არ არსებობის შემთხვევაში. ნახ. 2-ზე ილუსტრურებულია თავისუფალი ელექტრული და მექანიკური რხევევის პროცესების ანალოგიურობა. ნახაზზე მოყვანილია კონდენსატორის q(t) მუხტის ცვლილების და ტვირთის x(t) წონასწორობის მდგომარეობიდან გადახრის გრაფიკები, და ასევე J(t) დენისა და υ(t) ტვირთის სიჩქარის გრაფიკები რხევის ერთიდაიგივე
(*) განტოლება აღწერს თავისუფალ რხევებს LC-კონტურში, როცა არა არის მილევა. იგი ზუსტად ისევე გამოიყურება როგორც ზამბარაზე დამაგრებული ტვირთის რხევის განტოლება ხახუნის არ არსებობის შემთხვევაში. ნახ. 2-ზე ილუსტრურებულია თავისუფალი ელექტრული და მექანიკური რხევევის პროცესების ანალოგიურობა. ნახაზზე მოყვანილია კონდენსატორის q(t) მუხტის ცვლილების და ტვირთის x(t) წონასწორობის მდგომარეობიდან გადახრის გრაფიკები, და ასევე J(t) დენისა და υ(t) ტვირთის სიჩქარის გრაფიკები რხევის ერთიდაიგივე  პერიოდში.
პერიოდში.

ნახ. 2.
თავისუფალი ელექტრული და მექანიკური რხევების პროცესების ანალოგია
ზამბარაზე დამაგრებული ტვირთის თავისუფალი რხევების და რხევით ელექტრულ კონტურში მიმდინარე პროცესების შედარება ელექტრულ და მექანიკურ სიდიდეებს შორის ანალოგიის არსებობის შესახებ დასკვნის გაკეთების საშუალებას იძლევა. ეს ანლოგიები ცხრილშია მოცემული.
|
||||||||||||||||||||||||||||||||||||
|
ცხრილი 1 |
||||||||||||||||||||||||||||||||||||
როცა ადგილი არა აქვს მილევას, ელექტრულ კონტურში თავისუფალი რხევები ჰარმონიულია, ანუ მიმდინარეობს კანონით
q(t) = q0 cos(ωt + φ0).
რხევითი კონტურის L და C პარამეტრები მხოლოდ თავისუფალი რხევის საკუთარ სიხშირეს განსაზღვრავენ

ამპლიტუდა და საწყისი ფაზა საწყისი პირობებით განისაზღვრება, ანუ თუ რა საშუალებით მოხდა სისტემის წონასწორობიდან გამოყვანა. კერძოდ, რხევის პროცესისთვის, რომელიც კონტურში (ნახ. 1) დაიწყება K ჩამრთველის 2 მდგომარეობაში გადართვის შემდეგ, q0 = C , φ0 = 0.
, φ0 = 0.
თავისუფალი რხევებისას ხდება კონდენსატორში დამარაგებული WE ელექტრული ენერგიის კოჭას მაგნიტირ ენერგიად Wм პერიოდული გარდაქმნა და პირიქით. თუ რხევით კონტურში ენერგიის დანაკარგი არ არის, სისტემის სრული ელექტრომაგნიტური ენერგია უცვლელი რჩება:
\(W=W_{E}+W_{M}=\frac{q^{2}}{2C}+\frac{LJ^{2}}{2}=const\)
ყველა რეალური კონტური ელექტრულ R წინაღობას შეიცავს. მაშინ თავისუფალი რხევის პროცესი უკვე არ ემორჩილება ჰარმონიულ კანონს. ყოველი პერიოდის განმავლობაში კონტურში დამარაგებული ელექტრომაგნიტური ენერგიის ნაწილი ჯოულის სითბოდ გარდაიქმნება და რხევები ხდება მილევადი (ნახ. 3).

ნახ. 3.
კონტურის მილევადი რხევა
ელექტრულ კონტურში მილევადი რხევები ანალოგიურია ზამბარაზე დამაგრებული ტვირთის ბლანტი ხახუნის დროს მილევადი რხევისა, როცა ხახუნი სხეულის სიჩქარის პირდაპირპროპორციულად იცვლება: Fხახ = – βυ. ამ ფორმილაში კოეფიციენტი კონტურში ელექტრულო R წინაღობის ანალოგიურია. კონტურში თავისუფალი რხევის განტოლებას მილევის არსებობის შემთხვევაში აქვს სახე
 (**)
(**)
ფიზიკურ სიდიდეს δ = R / 2L მილევის კოეფიციენტი ეწოდება. ამ დიფერენციული განტოლების ამოხსნა არის ფუნქცია

რომელიც რხევის მილევის აღმწერ exp(–δt) მამრავლს შეიცავს. მილევის სიჩქარე კონტურის ელექტრულ R წინაღობაზეა დამოკირებული. იმ დროის შუალედს  , რომლის განმავლობაშიც რხევის ამპლიტუდა e ≈ 2,7 -ჯერ მცირდება, მილევის დრო ეწოდება.
, რომლის განმავლობაშიც რხევის ამპლიტუდა e ≈ 2,7 -ჯერ მცირდება, მილევის დრო ეწოდება.
მექანიკური რხევების თავში შემოტნილი იყო რხევითი სისტემის Q ვარგისიანობის ცნება:

სადაც N –მილევის τ დროის განმავლობაში სისტემის მიერ შესრულებული სრული რხევების რიცხვია. ნებისმიერი რხევითი სისტემის, რომელსაც თავისუფალი რხევების შესრულება შეუძლია, Q ვარგისიანობას შეიძლება ენერგეტიკული განსაზღვრა მიეცეს

RLC-კონტურისთვის ვარგისიანობა Q გამოისახება ფორმულით

რადიოტექნიკაში გამოყენებული ელექტრული კონტურების ვარგისიანობა ჩვეულებრივ რამოდენიმე ათეულის და ასეულის რიგისაცაა.
უნდა აღინიშნოს, რომ არც ისე დიდი ვარგისიანობის კონტურის თავისუფალი რხევების საკუთარი სიხშირე ω რამდენადმე ნაკლებია, იგივე L და C მნიშვნელობების მქონე, იდეალური კონტურის საკუთარ ω0 სიხშირეზე. მაგრამ როცა Q ≥ (5÷10) ეა განსხვავება შეიძლება უგულვებელვყოთ.
{loadnavigation}
მუდმივი დენის წრედებში გამტარზე ელექტრული მუხტის და წრედის უბნებზე დენების განაწილება სტაციონალურია, ე.ი. დროში არ იცვლება. ასეთ წრედებში ელექტრომაგნიტური ველი შედგება უძრავი მუხტის ელექტროსტატიკური ველისა და მუდმივი დენების მაგნიტური ველისაგან. ეს ველები ერთმანეთისგან დამოუკიდებლად არსებობენ.
თუ წრედის რაღაც უბანზე დენის ძალის ან დაძაბულობის ცვლილება ხდება, მაშინ წრედის სხვა უბნები ცვლილებას „იგრძნობენ“ მხოლოს რაღაც დროის შემდეგ, რომელიც სიდიდის რიგით წრედის ერთი წერტილიდან მეორემდე ელექტრომაგნიტური შეშფოთების გავრცელების τ დროის ტოლია. რადგანაც ელექტრომაგნიტური შეშფოთებები, c სინათლის სიჩქარის ტოლი, სასრული სიჩქარით ვრცელდებიან, ამიტომ 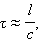 , სადაც l –წრედის ყველაზე უფრო დაშორებულ წერტილებს შორის მანძილია. თუ ეს τ დრო წრედის მიმდინარე პროცესის ხაგრძლივობაზე ბევრად ნაკლებია, მაშინ შეიძლება ჩაითვალოს, რომ დროის ყოველ მომენტში დენის ძალა ერთნაირია წრედის ყველა მიმდევრობით შეერთებულ უბანზე. ამგვარი პროცესებს ელექტრულ წრედებში და თვითონ წრედებს კვაზისტაციონალურს უწოდებენ.
, სადაც l –წრედის ყველაზე უფრო დაშორებულ წერტილებს შორის მანძილია. თუ ეს τ დრო წრედის მიმდინარე პროცესის ხაგრძლივობაზე ბევრად ნაკლებია, მაშინ შეიძლება ჩაითვალოს, რომ დროის ყოველ მომენტში დენის ძალა ერთნაირია წრედის ყველა მიმდევრობით შეერთებულ უბანზე. ამგვარი პროცესებს ელექტრულ წრედებში და თვითონ წრედებს კვაზისტაციონალურს უწოდებენ.
კვაზისტაციონალური პროცესები მუდმივი დენის კანონების საშუალებით შეიძლება იქნეს შესწავლილი, თუ ამ კანონებს წრედის უბნის დენის ძალისა და ძაბვის მეყსეული მნიშვნელობებისათვის გამოვიყენებთ.
სინათლის სუჩქარის ძალიან დიდი მნიშვნელობის გამო ელექტრულ წრედში წონასწორობის დამყარების დრო ძალიამ მცირეა. ამიტომ კვაზისტაციონალურს შეიძლება მივაკუთნოთ ბევრი ჩვეულებრივზე საკმაოდ სწრაფი პროცესი. მაგალითად, რადიოტექნიკურ წრედებში სწრაფი რხევები სიხშირეებით მილიონი რხევა წამში და უფრო დიდიც შეიძლება განხილული იქნეს როგორც კვაზისტაციონალური.
კვაზისტაციონალური პროცესის უბრალო მაგალითს შეიძლება წარმოადგენდნენ პეოცესები, რომლებიც RC- და RL-წრედებში მიმდინარეობენ მუდმივი დენის წყაროს ჩართვის გა გამორთვის დროს.
ნახ. 1-ზე გამოსახულია ელექტრული წრედი, რომელიც შედგება C ტევადობის კონდენსატორისა, R წინაღობის რეზისტორისა და  -ს ტოლი ემძ დენის წყაროსგან.
-ს ტოლი ემძ დენის წყაროსგან.
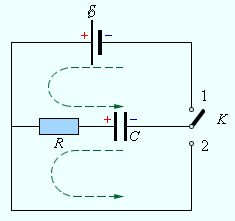
ნახ. 1.
კონდენსატორის რეზისტორის საშუალებით დამუხტვისა და განმუხტვის წრედი
თუ K ჩამრთველს ჩავკეტავთ 1 მდებარეობაში, მაშინ იწყება რეზისტორის საშუალებით დამუხტვის პროცესი. კვაზისტაციონალური წრედისთვის ომის კანონი ასე ჩაიწერება:
RJ + U =  ,
,
სადაც J – წრედში დენის ძალის მეყსეული მნიშვნელობაა, U – კონდენსატორის ძაბვის მეყსეული მნიშვნელიბა. წრედში დენის ძალა J ტოლია დროის ერთეულში კონდენსატორის მუხტის ცვლილებისა: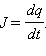 კონდენსატორის ძაბვა U დროის ნებისმიერ მომენტში ტოლია q/C. ამ თანაფარდობებიდან გამოდის
კონდენსატორის ძაბვა U დროის ნებისმიერ მომენტში ტოლია q/C. ამ თანაფარდობებიდან გამოდის

მივიღეთ კონდენსატორის დამუხტვის დიფერენციალური განტოლება. თუ კონდენსატორი თავიდან არ იყო დამუხტული, მაშინ ამ განტოლების ამოხსნას აქვს სახე
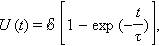
სადაც τ = RC – იმ წრედის ე.წ. დროის მუდმივაა, რომელიც რეზისტორისა და კონდენსატორისგან შედგება. სიდიდე τ პროცესის სიჩქარის მახასიათებელია. როცა t → ∞, U (t) →  . კონდენსატორის რეზისტორის საშუალებით დამუხტვის პროცესი ნახ. 2 (I)-ზეა ნაჩვენები.
. კონდენსატორის რეზისტორის საშუალებით დამუხტვის პროცესი ნახ. 2 (I)-ზეა ნაჩვენები.

ნახ. 2.
კონდენსატორის რეზისტორის საშუალებით დამუხტვა (I) და განმუხტვა(II)
თუ მას შემდეგ, რაც კონდენსატორი ბოლომდე დაიმუხტება  ძაბვამდე, K ჩამრთველი გადავრთოთ 2 მდგომარეობაში, მაშინ განმუხტვის პროცესი დაიწყება. განმუხტვის წრედში დენის გარე წყარო არ არის (
ძაბვამდე, K ჩამრთველი გადავრთოთ 2 მდგომარეობაში, მაშინ განმუხტვის პროცესი დაიწყება. განმუხტვის წრედში დენის გარე წყარო არ არის ( = 0). განმუხტვის პროცესი აღიწერება გამოსახულებით
= 0). განმუხტვის პროცესი აღიწერება გამოსახულებით
U (t) =  exp (–t / τ).
exp (–t / τ).
განმუხტვის პროცესში U (t) დამოკიდებულება გამოსახულია ნახ. 2 (II)-ზე. როცა t = τ კონდენსატორში ძავბა კლებულობს e ≈ 2,7 -ჯერ.
L ინდუქციურობის კოჭისა და R წინაღობის რეზისტორის შემცველ წრედშიც პროცესები ანალოგიურად მიმდინარეობს (ნახ. 3).

ნახ. 3.
L ინდუქციურობის კოჭის, R წინაღობის რეზისტორის და  -ს ტოლი ემძ-ს მქონე დენის წყაროს შემცველი წრედი
-ს ტოლი ემძ-ს მქონე დენის წყაროს შემცველი წრედი
თუ ნახ. 3-ზე გამოსახულ წრედში K ჩამრთველი ჩართულია და შემდეგ უეცრად გამოირთვება, მაშინ დაიწყება დების ჩამოყალიბების პროცესი. ყურადღება უნდა მიექცეს იმას, რომ სქემაში დენის წყაროსთან მიმდევრობით ჩართულია მცირე r წინაღობის რეზისტორი, რათა ჩართული K ჩამრთველის შემთხვევეში არ მოხდეს ბატარეის დამოკლება. რადგანაც r << R, დენის ჩამოყალიბების პროცესისათვის განტოლების დასაწერად ეს წინაღობა შეიძლება უგულვებელვყოთ. ამ პროცესს აღწერს განტოლება
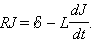
ეს განტოლება ჰგავს განტოლებას, რომელიც კონდენსატორის გამორთვას აღწერს, მაგრამ ამ შემთხვევაში ცვლად სიდიდეს დენის ძალა J წარმოადგენს. ამ განტოლების ამოხსნებს აქვს სახე
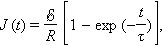
სადაც დროის მუდბივა τ = L / R. ანალოგიურად შეიძლება მივიღოთ K ჩამრთველის ჩართვისას RL-წრედში დენის შემცირების კანონი:
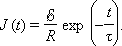
უნდა აღინიშნოს, რომ RC- და RL-წრედებში მიმდინარე პროცესები ბლანტ სითხეში სხეულის მოძრაობის მექანიკური პროცესების ანალოგიურია.








