{loadnavigation}
აინშტაინის ფარდობითობის პრინციპი ბუნების ყველა კანონის ინვარიანტობას ამტკიცებს ერთი ათვის ინერციული სისტემიდან მეორეში გადასვლის შემთხვევაში. ეს ნიშნავს, რომ ყველა განტოლება, რომლებიც ბუნების კანონებს აღწერენ, ინვარიანტული უნდა ივნენ ლორენცის გარდაქმნების მიბართ. ფარდობითობის სპეციალური თეორიის შექმნის მომენტისათვის ამ პირობებს, უკვე არსებული, მაქსველის ელექტროდინამიკა აკმაყოფილებდა. მაგრამ, ნიუტონის კლასიკური მექანიკის კანონები ლორენცის გარდაქმნებისადმი ინვარიანტული არ აღმოჩნდნენ, და ამიტომ ფარდობითობის სპეციალურმა თეორიამ მექანიკის კანონების გადახედვა და დაზუსტება მოითხოვა.
ასეთი გადახედვის საფუძველში აინშტაინმა ჩაკეტილ სისტემაში იმპულსისა და ენერგიის შენახვის კანონების შესრულების პირობა ჩადო. იმისათვიsს, რომ იმპულსის შენახვის კანონი ყველა ინერციულ ათვლის სისტემაში სრულდებიდეს, აუცილებელი გახდა სხეულის იმპულსის განმარტების შეცვლა. კლასიკური 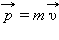 -ს ნაცვლად ფარდობითობის სპეციალურ თეორიაში
-ს ნაცვლად ფარდობითობის სპეციალურ თეორიაში 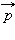 სიჩქარით მოძრავი m მასის სხეულის რელატივისრური იმპულსი
სიჩქარით მოძრავი m მასის სხეულის რელატივისრური იმპულსი 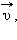 ჩაიწერება შემდეგი სახით:
ჩაიწერება შემდეგი სახით:
 (*)
(*)
თუ ასეთ განმარტებას მივიღებთ, მაშინ ურთიერთმოქმედი ნაწილაკების ჯამური იმპულსის შენახვის კანონი (მაგალითად, დაჯახებებისას) ლორენცის გარდაქმნებთან დაკავშირებულ ყველა ინერციულ სისტემაში შესრულდება. როცა β → 0 რელატივისტური იმპულსი კლასიკურში გადადის. იმპულსის გამოსახულებაში შემავალი m მასა ნაწილაკის ფუნდამენტური მახასიათებელია და არ არის დამოკიდებული ათვლის ინერციული სისტემის არჩევაზე, და ე.ი. მისი მოძრაობის სიჩქარეზე. (გასული წლების ბევრ სახელმძღვანელიში მას m0 ასოთი აღნიშნავდნენ და უძრაობის მასას უწოდებდნენ. გარდა ამისა, შემოჰქონდათ ე.წ. რელატივისტური მასა, რომელიც 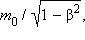 ტოლია, და დამოკიდებულია სხეულის მოძრაობის სიჩქარეზე. თანამედროვე ფიზიკა თანდათანობით უარს ამბობს ამ ტერმინოლოგიაზე).
ტოლია, და დამოკიდებულია სხეულის მოძრაობის სიჩქარეზე. თანამედროვე ფიზიკა თანდათანობით უარს ამბობს ამ ტერმინოლოგიაზე).
მატერიალური წერტილის რელატივისტური დინამიკის ძირითადი კანონი ისევე ჩაიწერება, როგორც ნიუტონის მეორე კანონი:
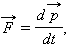
მხოლოდ ფარდობითობის სპეციალურ თეორიაში  -ში ნაწილაკის რელატივისტური იმპულსი იგულისხმება. აქედან გამომდინარე,
-ში ნაწილაკის რელატივისტური იმპულსი იგულისხმება. აქედან გამომდინარე,

რადგანაც რელატივისტური იმპულსი ნაწილაკის სიჩქარის პროპორციული არ არის, მისი ცვლილების სიჩქარე აჩქარების პირდაპირპროპორციული არ იქნება. ამიტომ სიდიდითა და მიმართულებით მუდმივი ძალა არ იწვევს თანაბარაჩქარებულ მოძრაობას.
მაგალითად, ღერძის გასწვრის ერთგანზომილებიანი მოძრაობის დროს ან წილაკის 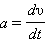 აჩქარება მუმივი ძალის მოქმედებით ტოლი აღმოჩნდება
აჩქარება მუმივი ძალის მოქმედებით ტოლი აღმოჩნდება
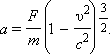
თუ კლასიკური ნაწილაკის სიჩქარე მუდმივი ძალის მოქმედებით უსაზღვროდ იზრდება, რელატივისტური ნაწილაკის სიჩქარეს არ შეუძლია გადააჭარბოს ვაკუუმში სინათლის სიჩქარეს. რელატივისტურ მექანიკაში, ნიუტონის მექანიკის მსგავსად, სრულდება ენერგიის შენახვის კანონი. სხეულის კინეტიკური ენერგია სხეულისათვის გარკვეული სიჩქარის მინიჭებისათვის საჭირო გარე ძალის მუშაობით განისაზღვრება. m მასის ნაწილაკი რომ ააჩქარო უძრაობის მდგომარეობიდან υ0 სიჩქარემდე მუდმივი F ძალის მოქმედებით, ამ ძალამ უნდა შეასრულოს მუშაობა
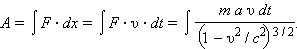
რადგანაც a dt = dυ, საბოლოოდ შეიძლება დაიწეროს

ამ ინტეგრალის გამოთვლას კინეტიკური ენერგიისათვის შემდეგ გამოსახულებამდე მივყავართ (ინდექსი „ნული“ სიჩქარის შემთხვევაში გამოტოვებულია):

აინშტაინი ამ გამოსახულების მარჯვენა ნაწილის პირველ წევრს ნაწილაკის მოძრაობის ნულოვანი ენერგიის E ინტერპრეტაციას აძლევდა, ხოლო მეორეს უძრაობის ენერგიისას E0:
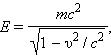 (**)
(**)
E0 = mc2. (***)
რელატივისტური დინამიკის კინეტიკური ენერგია Ek სხეულის სრული ენერგიისა E და მისი უძრაობის ენერგიის E0 სხვაობას წარმოადგენს:
Ek = E – E0.
ნახ. 1-ზე კლასიკურ და რელატივისტურ კანონებზე დამოკიდებული ნაწილაკის კინეტიკური ენერგიის ცვლილებაა ნაჩვენები.
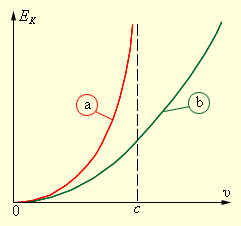
ნახ. 1.
კინეტიკური ენერგიის სიჩქარეზე დამოკიდებულება რელატივისტური (a) და კლასიკური (b) ნაწილაკისათვის. როცა υ << c კანონები ერთმანეთს ემთხვევა
რელატივისტური მექანიკის განსაკუთრებით მნიშვნელოვანია დასკვნა იმის შესახებ, რომ უძრაობის მდგომარეობაში მყოფი m მასა ენერგიის უზარმაზარ მარაგს შეიცავს. ამ მტკიცებულებას სხვადასხვაგვარი პრაქტიკული გამოყენება აქვს, ბირთვული ენერგიის გამოყენების ჩათვლით. თუ ნაწილაკის ან ნაწილაკთა სისიტემის მასა Δm -ით მცირდება, მაშინ ამ დროს უნდა გამოიყოფოდეს ენერგია ΔE = Δm · c2. მრავალრიცხოვანი პირდაპირი ექსპერიმენტები უძრაობის ენერგიის არსებობის დამაჯერებელ დასაბუთებას იძლევიან. აინშტაინის, მასასა და ენერგიის დამაკავშირებელი, ფორმულის პირველი ექსპერიმენტული დასაბუთება მიღებილი იყო რადიოაქტიური დაშლისას განთავისუფლებული ენერგიის შედარებით საწყისი ბირთვისა და ნარჩენების მასათა სხვაობასთან. მაგალითად, როცა თავისუფალი ნეიტრონის ბეტა-დაშლისას წარმოიქმნება პროტონი, ელექტრონი და კიდევ ერთი ნულოვანი მასის მქონე ნაწილაკი - ანტინეიტრინო:
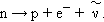
ამ დროს საბოლოო პროდუქტების ჯამური კინეტიკური ენერგია 1,25·10–13 ჯ-ს ტოლია. ნეიტრონის მასა აჭარბებს პროტონისა და ელექტრონის ჯამურ მასას Δm = 13,9·10–31 კგ-ით. მასის ასეთ შემცირებას უნდა შეესაბამებოდეს ენერგია ΔE = Δm · c2 = 1,25·10–13 ჯ, რომელიც დაშლის პროდუქტების დაკვირვებული კინეტიკურუ ენერგიის ტოლია.
რომ შეიქმნას ამ მოვლენის მასშტაბების შეგრძნება მაკროსამყაროში, ასეთი მაგალითი განვიხილოთ. 1 ტ ტრინიტროტოლუოლის აფეთქებისას თავისუფლდება 4,2·109 ჯ ენერგია. მეგატონიანი ბომბის აფეთქებისას გამოიყოფა 4,2·1015 კ ენერგია. ამ უზარმაზარი ენერგიის შესაბამისი მასა m = E / c2 მხოლოდ 46 გრამის ტოლია. ამგვარად, მეგატონიანი ბირთვული ბომბის აფეთქებისას ატომურმა „ასაფეთქებელმა“ უნდა მოიკლოს დაახლოებით 50გ-ით. წყალბადის ბომბის სრული საწყისი მასის ექვივალენტი სიმძლავრის მიხედვით 1 მეგატონიანი ტრინიტროლუოლი, დაახლოებით 1000-ჯერ მეტია და 50 კგ-ს შეადგენს.
მასისა და ენერგიის პროპორციულობის კანონი ფარდობითობის სპეციალური თეორიის ერთ-ერთ ყველაზე მნიშვნელოვან დასკვნას წარმოადგენს. მასა და ენერგია სხეულის განსხვავებული თვისებებია. მასა ახასიათებს მის ინერტულობასა და უნარს გრავიტაციული კავშირი დაამყაროს სხვა სხეულებთან. ენერგიის უმნიშვნელოვანეს თვისებას მისი უნარი წარმოადგენს, სხვადასხვა ფიზიკურ პროცესებში ერთი ფორმის ენერგიიდან ექვივალენტური რაოდენობით მეორე ფორმაში გადავიდეს. ამაში მდგომარეობს ენერგიის შენახვის კანონი. მასისა და ენერგიის პროპორციულობა მატერიის შინაგან ბუნებას გამოხატავს. აინშტაინის ფორმულა
E0 = mc2
ბუნების ფუნდამენტურ კანონს გამოსახავს, რომელსაც მასისა და ენერგიის ურთიერთკავშირის კანონს უწოდებენ.
რელატივისტური იმპულსის 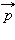 (*) გამოსახულებისა და სრული E ენერგიის გამოსახულების (**) კომბინირებით შეიძლება მივიღოს ამ სიდიდეების დამაკავშირებელი გამოსახულებები. ამისათვის მისახერხებელია (*) და (**) ფორმულები შემდეგი სახით გადავწეროთ:
(*) გამოსახულებისა და სრული E ენერგიის გამოსახულების (**) კომბინირებით შეიძლება მივიღოს ამ სიდიდეების დამაკავშირებელი გამოსახულებები. ამისათვის მისახერხებელია (*) და (**) ფორმულები შემდეგი სახით გადავწეროთ:
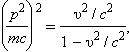 (*)
(*)
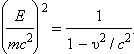 (**)
(**)
გამოკლებით მივიღებთ
E2 = (mc2)2 + (pc)2.
აქედან კიდევ ერთხელ გამოდის, რომ უძრავი ნაწილაკებისათვის (p = 0) E = E0 = mc2.
მიღებული დამოკიდებულება უჩვენებს, რომ ნაწილაკს შეიძლება ჰქონდეს ენერგია და იმპულსი, მაგრამ არ ჰქონდეს მასა (m = 0). ასეთ ნაწილაკებს უმასოებს უწოდებენ. უმასო ნაწილაკებისათვის ენერგიისა და იმპულსის დამოკიდებულება უბრალო ფორმულით გამოისახება.
E = pc.
უმასო ნაწილაკებს მიეკუთვნებიან ფოტონები - ელექტრომაგნიტური გამოსხივების ქვანტები და შესაძლოა, ნეიტრინო. უმასო ნაწილაკებს უძრაობის მდგომარეობაში არსებობა არ შეუძლიათ, ყველა ათვლის ინეციულ სისტემაში ისინი ზღვრული c სიჩქარით მოძრაობენ.
{loadnavigation}
გალილეის კლასიკური გარდაქმნები ფარდობითობის სპეციალურ თეორიაში არ გამოდგება, ამიტომ უნდა შეიცვალოს. ამ ახალმა გარდაქმნებმა კავშირი უნდა დაადგინოს K ათვლის სისტემაში დაკვირვებული ხდომილების დროის t მომენტსა და (x, y, z) კოორდინატებს და K' ათვლის სისტემაში დაკვირვებული იგივე ხდომილების t' დროის მომენტსა და (x', y', z') კოორდინატებს შორის.
კოორდინატებისა და დროის კინემატიკურ გარდაქმნის ფორმულებს ფარდობითობის სპეციალურ თეორიაში ლორენცის გარდაქმნებს უწოდებენ. ისინი ფარდობითობის სპეციალურ თეორიაის გამოჩენამდე 1904 წელს იყო შემოთავაზებული, როგორც გარდაქმნები რომლის მიმართაც ინვარიანტულია ელექტრომაგნიტური ფორმულები. იმ შმთხვევაში თუ K' სისტემა K სისტემის მიმართ υ სიჩქარით მოძრაობს x ღერძის მიმართ, მაშინ ლორენცის გარდაქმნებს აქვთ სახე:
K' → K K → K'
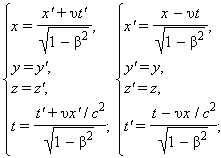
β = υ / c.
ლორენცის გარდაქმნებიდან მთელი რიგი შედეგები გამოდის. კერძოდ, მათგან გამოდის დროის შენელების რელატივისტური ეფექტი და სიგრძის ლორენცის შეკუმშვა. ვთქვათ, მაგალითად, K' სისტემის რაღაც x' წერტილში მიმდინარეობს τ0 = t'2 – t'1 (საკუთარი დრო) ხანგრძლივობის პროცესი, t'1 და t'2 – სადაც პროცესის დასაწყისისა და დასარულის შესაბამისი საათის ჩვენებებია K' სისტემაში. ამ პროცესის τ ხანგრძლივობა K სისტემაში ტოლი იქნება

ანალოგიურად, შეიძლება ვაჩვენოთ, რომ ლორენცის გარდაქმნიდან გამოდის სიგრძის შეკუმშვა. ლორენცის გარდაქმნების ერთ-ერთი უმნიშვნელოვანესი შედეგია დასკვნა ერთდროულობის ფარდობითობის შესახებ. ვთქათ, მაგალითად, ათვლის K' სისტემის ორ განსხვავებულ (x'1 ≠ x'2) წერტილში K' სისტემაში მყოფი დამკვირვებლისათვის ერთდროულად (t'1 = t'2 = t') მიმდინარეობს ორი ხდომილება. ლორენცის გარდაქმნებიდან გამომდინარე K სისტემის დამკვირვებელისთვის
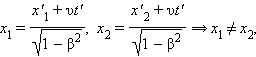
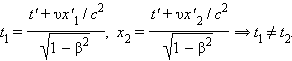
აქედან გამომდინარე, K სისტემაში ეს ხდომილებები, რჩებიან რა სივრცულად დაშორებულნი, აღარ იქნებიან ერთდროული. უფრო მეტიც, t2 – t1 სხვაობის ნიშანი υ(x'2 – x'1) გამოსახულების ნიშნით განისაზღვრება, ამიტომაც ზოგ ათვლით სისტემაში პირველი ხდომილება შეიძლება წინ უსწრებდეს მეორეს, მაშინ როცა სხვა ათვლით სისტემებში, პირიქით, მეორე ხდომილება უსწრებს პირველს. ფარდობითობის სპეციალური თეორიის ეს შედეგი არ ეხება მიზეზ-შედეგობრივი კავშირებით დაკავშირებულ ხდომილებებს, როცა ერთი ხდომილება მეორის ფიზიკურ შედეგს წარმოადგენს. შეიძლება ითქვას, რომ ფარდობითობის სპეციალური თეორია არ არღვევს მიზეზობრიობის პრინციპს და ხდომილებების მიზეზ-შედეგობრივი მონაცვლეობა ერთიდაგივეა ყველა ინერციულ ათვლის სისტემაში.
სივრცულად-გათიშული ხდომილებების ერთდროულობის ფარდობითობას შეიძლება შემდეგ მაგალითზე დავაკვირდეთ.
ვთქათ K'ათვილის სისტემის x' ღერძის გასწვრივ უძრავად გრძელი მყარი ძელაკი მდებარეობს. ძელაკის ცენტრში იმპულსური B ნათურა, ხოლო მის ბოლოებზე ორი სინქრონული საათია მოთავსებული (ნახ. 1(a)), K' სისტემა K სისტემის x ღერძის მიმართ υ სიჩქარით მოძრაობს. დროის რაღაც მომენტში ნათურა ძელაკის ბოლოებისკენ მოკლე იმპულსს აგზავნის. ორივე მიმართულების თანაბარუფლებიანობიდან გამომდინარე სინათლე K' სისტემაში ძელაკის ბოლოებამდე მივა ერთდროულად, და ძელაკის ბოლოებზე დამაგრებული საათები ერთიდაიგივე t' დროს აჩვენებენ. სისტემის მიმართ ძელაკის ბოლოები სიჩქარით მოძრაობენ ისე, რომ ერთი ბოლო მიძრაობს სინათლის იმპულსის შემხვედრი მიმაერთულებით, მეორე ბოლოს უწევს დაეწიოს სინათლეს. რადგანაც სინათლის იმპულსის გავრცელების სიჩქარე ორივე მიმართულებით ერთნაერია და ტოლია c -სი, K სისტემაში მყოფი დამკვირვებლისთვის სინათლე უფრო ჩქარა მარცხენა ბოლომდე მივა, ვიდრე მარჯვენამდე (ნახ. 1(b)).

ნახ http://suomenviagracialis.com/. 1.
ერთდროულობის ფარდობითობა. K' ათვილს სისტემაში სინათლის იმპულსი მყარი ძელაკის ბოლოებამდე ერთდროულად აღწევს (a) და სხვადასხვა დროს K ათვლის სისტემაში (b)
ლორენცის გარდაქმნები დროიში შუალედებისა და მანძილის ფარდობითობის ხასიათს გამოსახავს. მაგრამ ფარდობითობის სპეციალურ თეორიაში სივრცისა და დროის ფარდობითი ხასიათის მტკიცებულებების გვერდით მნიშვნელოვან როლს ასრულებს იმ ფიზიკური სიდიდეების ინვარიანტულობის დადგენა, რომლებიც არ იცვლებიან ერთი ათვლის სისტემიდან მეორეში გადასცლისას. ერთ-ერთ ასეთ სიდიდეს ვაკუუმში სინათლის გავრცელების სიჩქარე წარმოადგენს, რომელიც ფარდობითობის სპეციალურ თეორიაში აბსოლუტურ ხასიათს იძენს. მეორე მნიშვნელოვან ინვარიანტულ სიდიდეს, რომელიც სივრცულ-დროითი კავშირების აბსოლუტურ ხასიათს ასახავს, ხდომილებათა შორის ინტერვალია.
სივრცულ-დროითი ინტერვალი ფარდობითობის სპეციალურ თეორიაში შემდეგი თანაფარდობით განისაზღვრება:
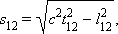
სადაც t12 – რაღაც ათვლით სისტემაში ხდომილებებს შორის დროის ინტერვალია, ხოლო l12 – იგივე სისტემაში განსაზღვრული იმ წერტილებს შორის მანძილი რომლებშიც ეს ხდომილებები ხდება. კერძო შემთხვევაში, როცა ერთ-ერთი ხდომილება ათვლის სისტემის კოორდინატთა სათავეში (x1 = y1 = z1 = 0) ხდება დროის t1 = 0 მომენტში, მეორე კი x, y, z კოორდინატების მქონე წერტილში დროის t მომენტში, ამ ხდომილებებს შორის სივრცულ-დროითი ინტერვალი ასე ჩაიწერება
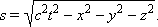
ლორენცის გარდაქმნების საშუალებით შეიძლება დამტკიცდეს, რომ ორ ხდომილებას შორის სივრცულ-დროითი ინტერვალი ერთი ინერციული ათვლის სისტემიდან მეორეზე გადასვლისას არ იცვლება. ინტერვალის ინვარიანტულობა ნიშნავს, რომ მანძილისა და დრო შუალედის ფარდობითობის მიუხედავად, ფიზიკური პროცესების მიმდინარეობას ობიექტური ხასიათი აქვს და ათვლის სისტემის არჩევაზე დამოკიდებული არ არის.
თუ ერთ-ერთ ხდომილებას კოორდინატთა სათავეში დროის t = 0 მომენტში სინათლის ხანლოკლე ანთება წარმოადგენს, ხოლო მეორეს სინათლის ფრონტის x, y, z კოორდინატების მქონე წერტილში დროის t მომენტში მოსვლა (ნახ. 3), მაშინ
x2 + y2 + z2 = c2t2,
და აქედან გამომდინარე, ინტერვალი ხდომილებათა ამ წყვილისთვის s = 0. ათვლის სხვა სისტემაში მეორე ხდომილების კოორდინატები და დრო სხვა იქნება, მაგრამ ამ სისტემაშიც სივრცულ-დროითი ინტერვალი s' ნულის ტოლი აღმოჩნდება, რადგანაც

სინათლის სიგნალით ერთმანეთთან დაკავშირებული ნებისმიერი ორი ხდომილებისთვის ინტერვალი ნულის ტოლია.
ლორენცის გარდაქმნებიდან კოორდინატებისა და დროისათვის შიეძლება მივიღოთ სიჩქარეების შეკრების რელატივისტური კანონი. ვთქვათ, მაგალითად K' ათვლით სისტემაში x' ღერძის გასწვრივ 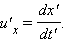 სიჩქარით მოძრაობს ნაწილაკი. ნაწილაკის სიჩქარის u'x და u'z მდგენელები ნულის ტოლია. K სისტემაში ამ ნაწილაკის სიჩქარე ტოლია
სიჩქარით მოძრაობს ნაწილაკი. ნაწილაკის სიჩქარის u'x და u'z მდგენელები ნულის ტოლია. K სისტემაში ამ ნაწილაკის სიჩქარე ტოლია 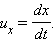 . ლორენცის გარდაქმნის ფორმულებიდან დიფერენცირების ოპერაციის გამოყენებით შეიძლება მივიღოთ:
. ლორენცის გარდაქმნის ფორმულებიდან დიფერენცირების ოპერაციის გამოყენებით შეიძლება მივიღოთ:
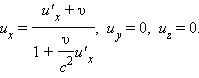
ეს თანაფარდობები სიჩქარეების შეკრების რელატივისტურ კანონს გამოსახავს. იმ შემთხვევისთვის, როცა ნაწილაკი პარალელურად 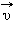 ფარდობითი სიჩქარით მოძრაობს K და K' ათვლის სისტემებში.
ფარდობითი სიჩქარით მოძრაობს K და K' ათვლის სისტემებში.
როცა υ << c რელატივისტური ფორმულები კლასიკური მექანიკის ფორმულებში გადადიან:
ux = u'x + υ, uy = 0, uz = 0.
თუ სინათლის იმპულსი K' სისტემაში x' ღერძის გასწვრივ სიჩქარით u'x = c ვრცელდება, მაშინ K სისტემაში ux სიჩქარისათვის მივიღებთ
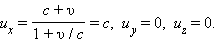
ამგვარად, K ათვლის სისტემაში სინათლის იმპულსი ასევე, x ღერძის გასწვლივ c სიჩქარით ვრცელდება, რაც თანხმობაშია სინათლის სიჩქარის ინვარიანტულობის პოსტულატთან.
{loadnavigation}
ვთქვათ მყარი ძელაკი უძრავადაა მოთავსებული ათვლის K' სისტემაში, რომელიც სიჩქარით მოძრაობს ათვლის ისიტემის მიმართ (ნახ. 1). ძელაკი x' ღერძის პარალელურადაა ორიენტირებული. მისი სიგრძე, რომელიც K' სისტემაში ეტალონური სახაზავითაა გაზომილი, l0-ს ტოლია. მას საკუთარ სიგრძეს უწოდებენ. როგორი იქნება ამ ძეალკის K სისტემაში მყოფი დამკვირვებლის მიერ გაზომილი სიგრძე? ამ კითხვაზე პასუხის გასაცემად აუცილებელია მოძრავი ძელაკის სიგრძის გაზომვის პროცედურა განიმარტოს.
ძელაკის l სიგრძეში K სისტემაში, რომლის მიმართაც ძელაკი მოძრაობს, იგულისხმება ძელაკის ბოლოების კოორდინატებს შორის მანძილი, რომელიც ამ სისტემის საათებით ერთდროულად დაფიქსირდა. თუ ცნობილია K' სისტემის სიჩქარე K სისტემის მიმართ, მაშინ მოძრავი ძელაკის სიგრძის გაზომვა შეიძლება დროის გაზომვამდე დაიყვანოს: υ სიჩქარით მოძრავი ძელაკის l სიგრძე υτ0 ნამრავლის ტოლია, სადაც τ0 – K სისტემის საათების მიხედვით დროის ინტერვალია სისტემის რაღაც უძრავი წერტილის (მაგალითად, A წერტილის) მიმართ ძელაკის დასაწყისისა და დაბოლოების გავლებს შორის (ნახ. 1). რადგანაც K სისტემაში ორივე ხდომილება (ფიქსირებული წერტილის მიმართ ძელაკის დასაწყისისა და დაბოლოების გავლა) ხდება ერთ წერტილში, დროის τ0 შუალედი K სისტემაში საკუთარ დროს წარმოადგენს. ამგვარად, მოძრავი ძელაკის l სიგრძე ტოლია l = υτ0.
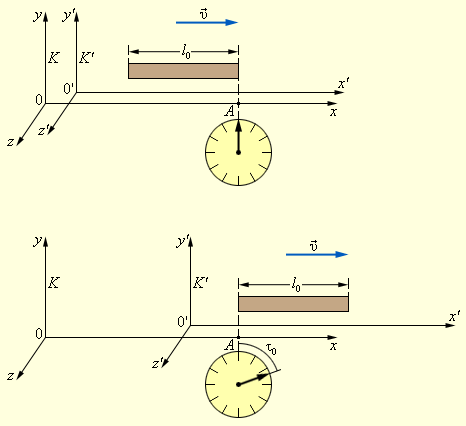
ნახ. 1.
მოძრავი ძელაკის სიგრძის გაზომვა
ახლა ვიპოვოთ კავშირი l და l0 შორის. K' სისტემის დამკვირვებლისათვის K სისტემის კუთვნილი A წერტილი უძრავი ძელაკის მიმართ მარცხნივ υ სიჩქარით, ამიტომ შეიძლება ჩაიწეროს
l0 = υτ,
სადაც τ K' სისტემის სინქრონული საათებით გაზომილი ძელაკის ბოლოებთან A წერტილის ჩავლის მომენტებს შორის დროის შუალედია. τ და τ0 დროის შუალედებს შორის კავშირის 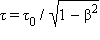 გამოყენებით, ვიპოვით
გამოყენებით, ვიპოვით

ამგვარად, ძელაკის სიგრძე იმ ათვლის სისტემის არჩევაზეა დამოკიდებული, რომელშიც ის იზომება, ე.ი. ფარდობით სიდიდეს წარმოადგენს. ძელაკის სიგრძე უდიდესი გამოდის იმ სისტემაში, რომელშიც ძელაკი უძრავია. დამკვირვებლის მიმართ მოძრავი სხეულები თავიანთი მოძრაობის მხარეს მოკლდებიან. ამ რალატივისტურ ფაქტს სიგრძის ლორენცის დამოკლებას (შეკუმშვას) უწოდებენ.
მანძილი არ არი აბსოლუტური სიდიდე, ის მოცემილი ათვლის სისტემის მიმართ სხეულის მოძრაობის სიჩქარეზეა დამოკიდებული. სიგრძის დამოკლება არ არის დაკავშირებული სხეულში მიმდინარე რაიმე პროცესთან. ლორენცის შეკუმშვა ახასიათებს სხეულის ზომის ცვლილებას მისი მოძრაობის მიმართულებით. თუ ძელაკს ნახ. 1-ზე მოვათავსებთ x ღერძის მართობულად, რომლის მიმართაც მოძრაობს K' სისტემა, მაშინ ძელაკის სიგრძე ორივე, K და K' სისტემის დამკვირვებლისთვის ერთნაირი აღმოჩნდება. ეს მტკიცებულება თანხმობაშია ყველა ინერციული სისტემის თანაბარუფლებიანობის პოსტულატთან. დასაბუთებისთვის შემდეგი აზრობრივი ექსპერიმენტი შეიძლება განვიხილოთ. K და K' სისტემებში y და y' ღერძების გასწვრივ მოვათავსოთ ორი მყარი ძელაკი. ძელაკებს ერთნაერი საკუთარი l სიგრძეები აქვთ, რომლებიც ძელაკებისადმი უძრავი K და K' სისტემის დამკვირვებლების მიერაა გაზომილი და ორივე ძელაკის ერთ-ერთი ბოლო კოორდინატთა O ან O' სათავეს ემთხვევა. გარკვეულ მომენტში ძელაკების ერთმანეთის გვერდი-გვერდ აღმოჩნდებიან და შესაძლებელი ხდება მათი პირდაპირი შედარება: ყოველი ძელაკის ბოლოს შეუძლია აღნიშვნა გააკეთოს მეორე ძელაკზე. თუ ეს აღმიშვნები ძელაკების ბოლოებს არ დაემთხვევა, ერთ-ერთი მატგანი მეორეძე გრძელი აღმოჩნდება ორივე ათვლის სიტემის თვალსაზრისით. ეს კი ფარდობითობის პრიციპის საწინააღმდეგო ფაქტი იქნებოდა.
საყურადღებოა, რომ მოძრაობის დაბალი (υ << c) სიჩქარეებისას ფარდობითობის სპეციალური თეორიის ფორმულები კლასიკურ თანაფარდობებში გადადიან: l ≈ l0 და τ ≈ τ0. ამგვარად, ნიუტონის მექანიკის კლასიკური წარმოდგენები, რომლებიც ნელ მოძრაობებზე დაკვირვების მრავალსაუკუნოვანი ექსპერიმენტული გამოცდილების საფუძველზე ჩამოყალიბდა, ფარდობითობის სპეციალურ თეორიაში ზღვრილ β = υ / c → 0 გადასვლას შეესაბამება. ამაში მდგომარეობს შესაბამისობის პრინციპი.
{loadnavigation}
ნებისმიერი ფიზიკური გაზომვის შესრულებისას უმნიშვნელოვანეს როლს ხდომილებებს შორის სივრცე-დროითი თანაფარდობა ასრულებს. ფარდობითობის სპეციალურ თეორიაში ხდომილება განისაზღვრება როგორც ფიზიკური მოვლევა, რომელიც არჩეულ ათვლის სისტემაში სივრცის რაიმე წერტილში დროის რაღაც მომენტში ხდება. ამგვარად, ხდომილება რომ ბოლომდე დახასიათდეს, საჭიროა არა მარტო მისი ფიზიკური შინაარსის გამოკვლევა, არამედ მისი ადგილისა და დროის განსაზღვრა. ამისათვის აუცილებელია მანძილისა და დროის შუალედების გაზომვის პროცედურების გამოყენება. აინშტაინმა აჩვენა, რომ ეს პროცედურები მკაცრ გასაზღვრას საჭიროებან.
იმისთვის, რომ არჩეულ ათვლით სისტემაში სივრცის ერთსადაიმავე წერილში მიმდინარე ორ ხდომილებას შორის (მაგალითად რაიმე პროცესის დასაწყისსა და დასასრულს შორის) დროის შუალედის გაზომვა შესრულდეს, საკმარისია ეტალონური საათის ქონა. დღეისთვის ყველაზე დიდ სიზუსტით ამიაკის მოლეკულების (მოლეკულური საათი) ან ცეზიუმის ატომების (ატომური საათი) საკუთარ რხევებზე დაფუძვნებული საათები გამოირჩევიან. დროის შუალედების გაზომვა ემყარება ერთდროულობის ცნებას: რაიმე პროცესის ხანგრძლივობა იმ დროის შუალედთან შედარებით განისაზღვრება, რომელიც საათის პროცესის დაწყების ერთდროულ ჩვენებასა და იგივე საათის პროცესის დასრულების ერთდროულ ჩვენებას აშორებს ერთმანეთისაგან. თუ ორივე ხდომილება სხვადასხვა ათვლის სისტემაში ხდება, მათ შორის დროის შუალედის გაზომვისთვის ამ წერტილებში უნდა იყოს სინქრონიზებული საათები.
საათების სინქრონიზაციის პროცესის აინშტაინისეული განმარტება დამყარებულია იმაზე, რომ ვაკუუმში სინათლის სიჩქარე დამოკიდებული არ არის გავრცელების მიმართულებაძე. ვთქვათ A წერტილიდან A-ს საათის მიხედვით დროის t1 მომენტში გამოდის სინათლის მოკლე იმპულსი (ნახ. 1). ვთქვათ B წერტილში მოსვლის და უკან არეკვლის დრო B -ს საათზე ტოლია t'. და ბოლოს, ვთქვათ არეკვლილი სიგნალი A -ში ბრუდება A-ს საათის მიხედვით დროის t2 მომენტში. მაშინ, განმარტების მიხედვით A და B-ში საათები სინქრონული იქნება, თუ t' = (t1 + t2) / 2.
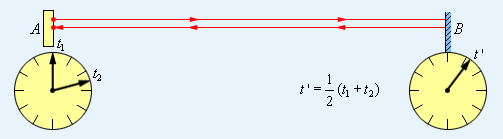
ნახ. 1.
საათების სინქრონიზაცია ფარდობითობის სპეციალური თეორიის მიხედვით
ათვლის სისტემის არჩევისგან დამოუკიდებელი ერთიანი მსოფლიო დროის არსებობა, რაც უცილობელ ფაქტად ითვლებოდა კლასიკურ ფიზიკაში, უსასრულოდ დიდი სიჩქარით მოძრავი სიგნალის საშუალებით საათების სინქრონიზაციის არაპირდაპირი დაშვების ექვივალენტურია.
ამგვარდ, არჩეული ათვლის სისტემის სხვადასხვა წერტილებში სინქრონული საათების განლაგება შეიძლება. ახლა შესაძლებელია სივრცულად განსხვავებელ წერტილებში მიმდინარე ხდომილებათა ერთდროილობის ცნების განმარტება: ეს ხდომილებები ერთდროულია, თუ სინქრონიზირებული საათები ერთსადაიმავე დროს აჩვენებენ.
ახლა განვიხილოთ მეორე ინერციული K' სისტემა , რომელიც K სისტემის x ღერძის დადებითი მიმართულებით რაღაც υ სიჩქარით მოძრაობს. ამ ახალი ათვლის სისტემის სხვადასხვა წერტილებში ასევე შეაძლებელია საათების განლაგება და მათი ზემოთ აღწერილი პროცედურის მიხედვით სინქრონიზაცია. ახლა უკვე ორ ხდომილებას შორის დროის ინტერვალი შეიძლება გაიზომოს როგორც K სისტემის, ასევა K' სისტემის საათებით. იქნებიან თუ არა ეს ინტერვალები ერთნაერი? ამ კითხვაზე პასუხი ფარდობითობის სპეციალური თეორიის პოსტულატებთან თანხმობაში უნდა იყოს.
ვთქვათ ორივ ხდომილება K' სისტემაში ერთსადაიმავე წერტილში ხდება და მათ შორის დროის შუალედი K' სისტემის საათით τ0 ტოლია. დროის ამ შუალედს საკუთარ დროს უწოდებენ. როგორი იქნება დროის შუალედი იგივე ხდომილებებს შორის, თუ მას K სისტემის საათით გავზომავთ?
ამ კითხვაზე პასუხის გასაცემად განვიხილოდ შემდეგი აზრობრივი ექსპერიმენტი. რაღაც l სიგრძის მყარი ძელაკის ერთ-ერთ ბოლოზე მიმაგრებულია იმპულსური ნათურა B, ხოლო მეორე ბოლოზე - ამრეკლი სარკე M. ძელაკი K' სისტემაში მოთავსებულია უძრავად და y' ღერძის პარალელურადაა ორიენტირებული (ნახ. 2). ხდომილება 1 – ნათურის ანთება, ხდომილება 2 – მოკლე სინათლის იმპულსის ნათურასთან დაბრუნება.

ნახ. 2.
დროის შუალედების ფარდობითობა. K' სისტემაში ხდომილებების დადგომის მომენტი ერთიდაიგიცე C საათით ფიქსირდება, K სისტემაში კი - ორი სინქრონიზებული სივრცილად დაშორებული C1 და C2 საათით. K' სისტემა მოძრაობს υ სიჩქარით K სისტემის x ღერძის დადებითი მიმართულებით
K' სისტემაში ორივე განსახილველი ხდომილება ერთსადაიმავე წერტილში ხდება. მათ შორის დროის შუალედი (საკუთარი დრო) ტოლია τ = 2l /. K სისტემაში მყოფი დამკვირვებლისთვის სინათლის იმპულსი სარკეებს შორის მოძრაობს ზიგზაგისებურად და გადის 2L მანძილს, რომელიც ტოლია

სადაც τ – K სისტემაში ბდებარე C1 და C2 სინქრონული საათებით გაზომილი სინათლის იმპულსის გამოსვლასა და დაბრუნებას შორის დროის შუალედია. მაგრამ, ფარდობითობის სპეციალური თეორიის მეორე პოსტულატის მიხედვით K სისტემაში სინათლის იმპულსი იგივე c სიჩქარით მოძრაობდა, როგორითაც K' სისტემაში. აქედან გამომდინარე, τ = 2L / c.
ამ თანაფარდობებიდან შეიძლება τ-სა და τ0-ს შორის დამოკიდებულების პოვნა:

სადაც β = υ / c.
ამგვარად, ორ ხდომილებას შორის დროის შუალედი ათვლის სისტემაზეა დამოკიდებული, ე.ი. ფარდობითია. საკუთარი დრო ყოველთვის ნაკლებია, ვიდრე ნებისმიერ სხვა ათვლით სისტემაში გაზომილი ამ ხდომილებათა შორის დროის შუალედი. ამ ფაქტს რელატივისტურად შენელებული დრო ეწოდება. დროის შენელება სინათლის სიჩქარის ინვარიანტულობის შედეგია.
დროის შენელების ეფექტი K და K' ინერციული სისტემების თანაბარუფლებიანიბის პოსტულატიდან გამომდინარე ურთიერთშექცევადია: ნებისმიერი დამკვირვებლისათვის K ან K' -ში დამკვირვებლის მიმართ მოძრავ სისტემასთან დაკავშირებული საათი უფრო ნელა მიდის (მუშაობს). ეს დასკვნა ფარდობითობის სპეციალური თეორიის პირდაპირი ცდისეული დადასტურებაა. მაგალითად, კოსმოსური სხივების შესწავლისას მათ შემადგენლობაში აღმოჩნდა μ-მეზონები - ელემენტარული ნაწილაკები, რომელთა მასა დაახლოებით 200-ჯერ აჭარბებს ელექტრონის მასას. ეს ნაწილაკები სტაბილურები არ არიან, მათი სიცოცხლის საშუალო საკუთარი დრო ტოლია τ0 = 2,2·10–6 წმ. მაგრამ კოსმოსურ სხივებში μ-მეზონები მოძრაობენ სინათლის სიჩქარის მახლობელი სიჩქარით. დროის შენელების რელატივისტური ეფექტის გათვალისწინების გარეშე ისინი ატმოსფეროში გაიფრენდნენ cτ0 ≈ 660 მ ტოლ მანძილს. სინამდვილეში, როგორც გამოცდილება უჩვენებს, მეზონები სიცოცხლის დროის განმავლობაში დაშლის გარეშე გაცილებით დიდ მანძილის გავლას ასწრებენ. ფარდობითობის სპეციალური თეორიის მიხედვით, მეზონის სიცოცხლის საშუალო დრო დედამიჭაზე მყოფი დამკვირვებლის საათის მიხედვით ტოლია 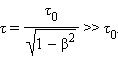 , რადგანაც β = υ / c ერთთან ახლოა. ამიტომ დედემიწასთან დაკავშირებულ ათვლის სისტემაში მეზონის მიერ გავლილი საშუალო მანძილი υτ 660 მ-ზე გაცილებით მეტი აღმოჩნდება.
, რადგანაც β = υ / c ერთთან ახლოა. ამიტომ დედემიწასთან დაკავშირებულ ათვლის სისტემაში მეზონის მიერ გავლილი საშუალო მანძილი υτ 660 მ-ზე გაცილებით მეტი აღმოჩნდება.
დროის შენელების რელატივისტურ ეფექტთან დაკავშირებულია ე.წ. „ტყუპების პარადოქსი“. იგულისმება, რომ ერთ-ერთი ტყუპისცალი დარჩა დედამიწაზე და მეორე მიემგზავრება ხანგრძლივ კოსმოსურ მოგზაურობაში სუბსინათლის სიჩქარით. დედამიწაზე მყოფი დამკვირვებლისათვის კოსმოსურ ხომალდში დრო უფრო ნელა მიდის, და როცა ასტრონავტი დედამიწაზე ბრუნდება, ის თავის დედამიწაზე დარჩენილ ტყუპისცალ ძმაზე გაცილებით ახალგაზრდა იქნება. პარადოქსი იმაში მდგომარეობს, რომ იგივე დასკვნა შეუძლია გააკეთოს მეორე, მოგზაურობაში წასულ ტყუპიაცალსაც. მისთვის დრო დედამიწაზე მიდის უფრო ნელა, და შეუძლია ელოდოს, რომ ანგრძლივი მოგზაურობიდან დაბრუნებულს დედამიწაზე დარჩენილი ძმა მასთან შედარებით გაცილებით ახალგაზრდა დახვდება.
„ტყუპების პარადოქსის“ გადასჭრელად მხედველობაში უნდა იქნეს მიღებული იმ ათვლის სისტემების არათანაბარუფლებიანობა, რომლებშიც ძმები იმყოფებიან. პირველი მათგანი, დედამიწაზე დარჩენილი, მთელი ამ დროის განმავლობაში ინერციულ სისტემაში იმყოფებოდა, მაშინ როცა კოსმოსურ ხომალდთან დაკავშირებული ათვლის ისიტემა პრინციპულად არაინერციულია. კოსმოსური ხომალდი განიცდის აჩქარებას სტარტის აღების, ტრაექტორიის შორეულ წერტილში მოძრაობის მიმართულების შეცვლის და დედამიწაზე დაჯდომის მომენტში. ამიტომ, ასტრონავტი ძმის დასკვნა სწორი არ არის. ფარდობითობის სპეციალური თეორია წინასწარმეტყველებს, რომ ის მართლაც დედამიწაზე დარჩენიზე ახალგაზრდა იქნება.
თუ კოსმოსური ხომალდის სიჩქარე სინათლის c სიჩქარეზე გაცილებით ნაკლებია, დროის შენელების ეფექტი იმდენად უმნიშვნელოა, რომ შესაძლებელია მისი უგულვებეყოფა. მიუხედავად ამისა, ამ ეფექტის პირდაპირი დასაბუთაბა გახდა შესაძლებელი მაკროსკოპული საათების ექსპერიმენტის საშუალებით. ყველაზე უფრო ზუსტი საათი ცეზიუმის ატომების ნაკადზე მომუშავე ატომური საათია. ეს საათი წამში 9192631770-ჯერ „წიკწიკებს“. 1971 წელს ამერილელმა ფიზიკოსებმა შეადარეს ორი ასეთი საათი, ისე რომ ერთი ჩვეულიბრივი რეაქტიული თვითმფრინავით დედამიწის გარშემო დაფრინავდა, მეორე კი დედამიწაზე, აშშ-ს სამხედრო-საზღვაო ობსერვატორიაში იმყოფებოდა. ფარდობითობის სპეციალური თეორის თანახმად, მოგზაურობაში მყოფი საათი დედამიწაზე მყოფს (184 ± 23)·10–9 წმ-ით უნდა ჩამორჩენოდა. დაკვირვებულმა ჩამორჩენამ (203 ± 10)·10–9 წმ შეადგინა, ე.ი. დაკვირვების ცდომილების ფარგლებში. რამოდენიმე წლის შემდეგ ექსპერიმენტი გაიმეორეს დამიიღეს ფარდობითობის სპეციალური თეორიასთან 1%-იანი თანხმობა.
დღეისათვის უკვე აუცილებელია, ატომური საათების შორ მანძილზე ტრანსპორტირების შემთხვევაში, საათის შენელების რელატივისტური ეფექტის მხედველობაში მიღება
