{loadnavigation}
აინშტაინის მოერ 1905 წელს ფოტოეფქტის ასახსნელად შემოთავაზებულმა ელექტრონების კონცენტრაციამ ექსპერიმენტული დასაბუთება ამერიკელი ფიზიკოსის ა.კომპტონის ცდებში ჰპოვა. კომპტონი სწავლობდა მოკლეტალღოვანი რენტგენული გამოსხივების დრეკად გაბნევას ნივთიერების თავისუფალ (ატომებთან სუსტად დაკავშირებულ) ელექტრონებზე. მის მიერ აღმოჩენილი გაბნეული გამოსხივების ტალღის სიგრძის გაზრდის ეფექტი, რომელსაც შემდგომში კომპტონის ეფექტი ეწოდა, არ თავსდებოდა ტალღური თეორიის ჩარჩოებში, რომლის მიხედვითაც გამოსხივების ტალღის სიგრძე გაბნევისას არ უნდა იზრდებოდეს. ტალღური თეორიის თანახმად, ელექტრონი სინათლის ტალღის პერიოდული ველის მოქმედებით ასრულებს იძულებით რხევას ამ ტალღის სიხშირეზე და ამიტომ გაბნეული ტალღებიც იგივე სიხშირის არიან.
ნახ. 1-ზე კომპტონის სქემაა მოცემული. λ0 ტალღის სიგრძის მონოქრომატული რენტგენული გამოსხივებაა, რომელიც რენტგენის R მილიდან გამოდის, ტყვიის დიაფრაგმების გავლით, ვიწრო კონის სახით მიემართება გამბნევ ნივთიერება-სამიზნეზე (გრაფიტი, ალუმინი). θ კუთხით გაბნეული გამოსხივების ანალიზი რენტგენული სხივების S სპექტოგრაფის საშუალებით ხდება, რომელშიც დიფრაქციული მესერის როლს მბრუნავ მაგიდაზე დამაგრებული K კრისტალი ასრულება. ცდა უჩვენებს, რომ გაბნეულ გამოსხივებაში დაიკვირვება ტალღის სიგრძის Δλ გადიდება, რომელიც გაბნევის θ კუთხეზეა დამოკიდებული:

სადაც Λ = 2,43·10–3 ნმ – ე.წ. კომპტონის ტალღის სიგრძეა, რომელის გამბნევის ნივთიერების თვისებებზე არ არის დამოკიდებული. გაბნეულ გამოსხივებაში λ ტალღის სიგრძის სპექტრული ხაზების გვერდით დაიკვირვება λ0 ტალღის სიგრძის წანაცვლებული ხაზი. წანაცვლებული და წაუნაცვლებელი ხაზების ინტენსივობათა ფარდობა გამბნევი ნივთიერების გვარობაზეა დამოკიდებული.
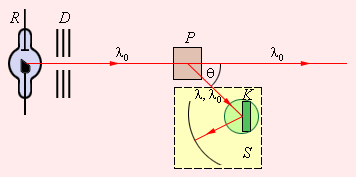
ნახ. 1.
კომპტონის ექსპერიმენტის სქემა
ნახ. 2-ზე გარკვეული კუთხით გაბნეული გამოსხივების სპეტრში ინტენსივობათა განაწილების მრუდებია წარმოდგენილი.
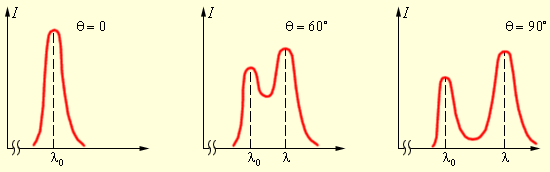
ნახ. 2.
გაბნეული გამოსხივების სპექტრი
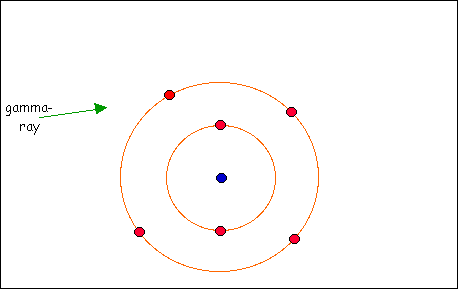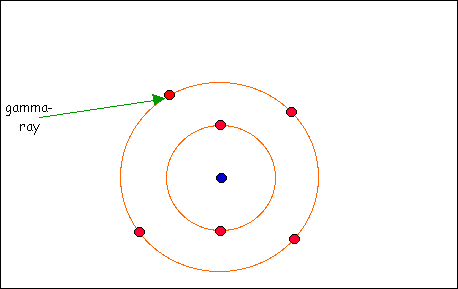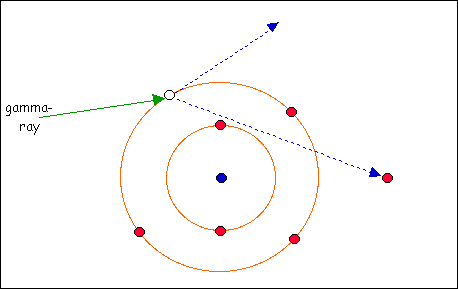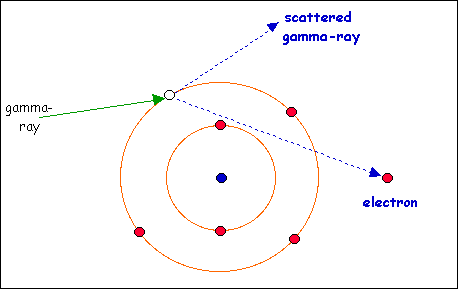
კომპტონის ეფექტი გამოსხივების ბუნების კვანტური წარმოდგენების საფუძველზე 1923 წელს ერთმანეთისაგან დამოუკიდებლად კომპტონმა და დებაიმ ახსნეს. თუ, მივიღებთ, რომ გამოსხივება ფოტონების ნაკადს წარმოადგენს, მაშინ კომპტონის ეფექტი რემტგენული ფოტონების ნივთიერების ელექტრონებთან დრეკადი შეჯახების შედეგია. გამბნევი ნივთიერების მსუბუქ ატომებში ელექტრონები სუსტ კავშირშია ატომის ბირთვებთან, ამიტომ ისინი თავისუფლებად შეიძლება ჩაითვალონ. შეჯახების პროცესში ფოტონი ელექტრონს, შენახვის კანონების თანახმად, გადასცემს თავისi ენერგიისა და იმპულსის ნაწილს.
განვიხილოთ ორი ნაწილაკის დრეკადი შეჯახება - მოძრავი ფოტონი, რომელსაც E0 = hν0 ენერგია და p0 = hν0 / c იმპულსი აქვს და ელექტრონი, რომლის უძრაობის ენერგია 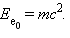 ტოლია. ფოტონი ელექტრონთან დაჯახებისას იცვლის მოძრაობის მიმართულებას (გაიბნევა). გაბნევის შემდეგ ფოტონის იმპულსი p = hν / c-ს ტოლი ხდება, ხოლო მისი ენერგია კი E = hν < E0. ფოტონის ენერგიის შემცირება სიხშირის გადიდებას ნიშნავს. ელექტრონის ენერგია დაჯახების შემდეგ, რელატივისტური ფორმულის თანახმად ხდება
ტოლია. ფოტონი ელექტრონთან დაჯახებისას იცვლის მოძრაობის მიმართულებას (გაიბნევა). გაბნევის შემდეგ ფოტონის იმპულსი p = hν / c-ს ტოლი ხდება, ხოლო მისი ენერგია კი E = hν < E0. ფოტონის ენერგიის შემცირება სიხშირის გადიდებას ნიშნავს. ელექტრონის ენერგია დაჯახების შემდეგ, რელატივისტური ფორმულის თანახმად ხდება  ტოლი, სადაც pe – ელექტრონის მიერ მიღებული იმპულსია. შენახვის კანონი ჩაიწერება შემდეგი სახით
ტოლი, სადაც pe – ელექტრონის მიერ მიღებული იმპულსია. შენახვის კანონი ჩაიწერება შემდეგი სახით
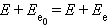
ან

იმპულსის შენახვის კანონი
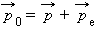
კოსინუსების გამოყენებით შეიძლება გადაიწეროს სკალარული ფორმით (იხ. იმპულსების დიაგრამა ნახ. 3):
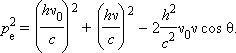


ნახ. 3.
უძრავ ელექტრონზე ფოტონის დრეკადი გაბნევის იმპულსების დიაგრამა
ენერგიისა და იმპულსის შენახვის კანონების ორი გამოსახულების საშუალებით, რამდენიმე გარდაქმნისა და pe სიდიდის გამორიცხვის შემდეგ შეიძლება მივიღოთ
mc2(ν0 – ν) = hν0ν(1 – cos θ).
სიხშირეებიდან ტალღის სიგრძეებზე გადასვლა 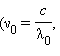
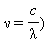 გვაძლევს გამოსახულებას, რომელიც ექსპერიმენტულად მიღებულ კომპტონის ფორმულას ემთხვევა:
გვაძლევს გამოსახულებას, რომელიც ექსპერიმენტულად მიღებულ კომპტონის ფორმულას ემთხვევა:
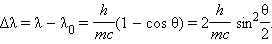
ამგვარად, ქვანტურ წარმოდგენებზე (წარმოდგენებზე) დაყრდნობით გაკეთებულმა თეორიულმა გათვლებმა ამომწურავად ახსნა კომპტონის ეფექტი და შესაძლებელი გახადა კომპტონის Λ ტალღის სიგრძის ფუნდამენტური მუდმივებით h, c და m-ით გამოსახვა:
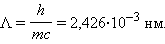
რაგორც ცდამ უჩვენა, გაბნეულ გამოსხივებაში წანაცვლებული λ ტალღის სიგრძის ხაზის გვერდით დაიკვირვება წანაცვლებელი საწყისი λ0 ტალღის სიგრძით. ეს ფოტონების ნაწილის ატომებთან მყარად დაკავშირებულ ელექტრონთა ურთიერთქმედებით აიხსნება. ამ შემთხვევაში ფოტონი ენერგიასა და იმპულს მთელ ატომთან ცვლის. ატომის, ელექტრონთან შედარებით, დიდი მასის გამო ატომს ფოტონის ენერგიის მხოლოდ უმნიშვნელო ნაწილი გადაეცემა, ამიტომაც გაბნეული გამოსხივების λ ტალღის სიგრძე პრაქტიკულად არ განსხვავდება დაცემული გამოსხივების λ0 ტალღის სიგრძისაგან.
{loadnavigation}
ფოტოელექტრული ეფექტი 1887 წელს იქნა აღმოჩენილი გარმანელი ფიზიკოსის ჰ.ჰერცის მიერ. ფოტოეფექტის მოვლენის ყველაზე სრული გამოკვლევა 1900 წელს ფ.ლენარდმა შეასრულა. ამ დროისათვის უკვე აღმოჩენილი იყო ელექტრონი (1897 წ. ჯ.ტომსონი), და ნათელი გახდა, რომ ფოტოეფექტი (ან უფრო სწორად -გარე ფოტოეფექტი) ნივთიერებიდან მასზე დაცემული სინათლის მიქმედებით ელექტრონების ამოგდებაში მდგომარეობს.
ნახ. 1-ზე გამოსახულია ფოტოეფექტის გამოსაკვლევი ექსპერიმენტული დანადგარის სქემა.
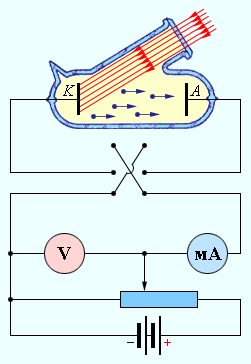
ნახ. 1.
ფოტოეფექტის შესასწავლი ექსპერიმენტული დანადგარის სქემა.
ექსპერიმენტში გამოყენებული იყო მინის ვაკუუმური ბალონი მეტალის ორი ელექტროდით ზედმიწევნით გასუფთავებული ზედაპირებით. ელექტრონებზე მოდებული იყო გარკვეული U ძაბვა, რომლის პოლარობის შეცვლა ორმაგი გადამრთველის შასუალით შეიძლებოდა. ერთ-ერთი ელექტროდი (კათოდი K) კვარცის სარკმლიდან გარკვეული λ ტალღის სიგრძის მონოქრომატული სინათლით ნათდებოდა. სინათლის უცვლელი ნაკადის პირობებში ხდებოდა ფოტოდენის I ძალის მოდებულ ძაბვაზე დამოკიდებულების დაკვირვება. ნახ. 2-ზე ამგვარი დამოკიდებულების ტიპური მრუდებია გამოსახული, რომლებიც კათოდზე დაცემული სინათლის ნაკადის ორი მნიშვნევობისთვისაა მიღებული.
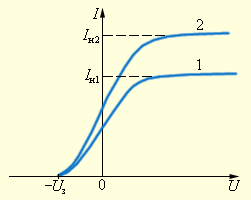
ნახ. 2.
ფოტოდენის I ძალის დამოკიდებულება მოდებულ ძაბვაზე. მრუდი 2 შეესაბამება უფრო დიდი ინტენსივობის სინათლის ნაკადს შეესაბამაბა. Iн1 და Iн2 – გაჯერების დენებია, Uз – ჩამკეტი პოტენციალი
მრუდები უჩვენებენ, რომ საკმარისად დიდი დადებითი ძაბვის შემთხვევაში A ანოდზე ფოტოდენი გაჯერებულ მდგომარეობას აღწევს, რადგანაც სინათლის მიერ ამიგლეჯილი ყველა ელექტრონმა მიაღწია ანოდს. ფაქიზმა გაზომვებმა უჩვენეს, რომ გაჯერების დენი დაცემული სინათლის ინტენსივობის პირდაპირპროპორციულია. როცა ანოდზე ძაბვა უარყოფითია, ანოდსა და კათოდს შორის ელექტრული ველი ელექტრონებს ამუხრუჭებს. ანოდს შეუძლია მიაღწოის მხოლოდ იმ ელექტრონებმა, რომელთა კინეტიკური ენერგია |eU| -ს აჭარბებს. თუ ძაბვა ანოდზე Uз -ზე ნაკლებია, ფოტოდენი წყდება. Uз-ის გაზომვით შეიძლება ფოტოელექტრონების მაქსიმალური კინეტიკური ენერგიის განსაზღვრა:
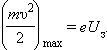
მეცნიერთა გასაოცრად, U3-ის სიდიდე არ აღმოცნდა დამოკიდებული დაცემული სინათლის ინტენსივობაზე. ფაქიზმა გაზომვებმა უჩვენეს, ჩამკეტი პოტენციალი სინათლის სიხშირის ზრდისას წრფივად იზრდება (ნახ. 3).
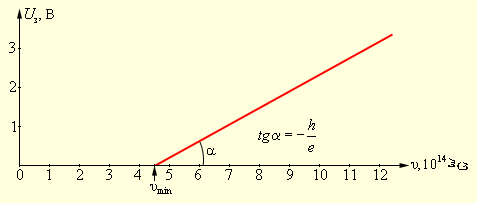
ნახ. 3.
ჩამკეტი პოტენციალის Uз დამოკიდებულება დაცემული სინათლის ν სიხშირეზე
მრავალრიცხოვანი ექსპერიმენტატორების მიერ დადგინდა ფოტოეფექტის შემდეგი ძირითადი კანონზომიერებები:
- ფოტოელექტრონების მაქსიმალური კინეტიკური ენერგია წრფივად იზრდება სინათლის სიხშირის გაზრდით და არ არის დამოკიდებული მის ინტენსივობაზე.
- ყოველი ნივთიერებისათვის არსებობს ე.წ. ფოტოეფექტის წითელი საზღვარი, ე.ი. უმცირესი νmin სიხშირე, რომლის დროსაც ჯერ კიდევ შესაძლებელია გარე ფოტოეფექტი.
- კათოდიდან სინათლის მიერ ერთ წამში ამოგლეჯილი ელექტრონების რიცხვი სინათლის ინტენსივობის პირდაპირპროპორციულია.
- ფოტოეფქტი პრაქტიკულად უინერციოა, თუ სინათლის სიხშირე ν > νmin, ფოტოდენი აღიძვრება კათოდის განათების დაწყების თანავე მყისიერად.
ფოტოეფექტის ყველა ეს კანონზომიერება ძირეულად ეწინააღმდეგებოდა კლასიკური ფიზიკის წარმოდგენებს სინათლის ნივთიერებასთან ურთიერთქმედების შესახებ. ტალღური წარმოდგენების თანახმად სინათლის ელექტრომაგნიკური ტალღის საშუალებით ელექტრონს თანდათან უნდა დაეგროვებინა ენერგია, სინათლის ინტენსივიბაზე დამოკიდებული მნიშვნელოვანი დრო იქნებიდა საჭირო, იმისათვის რომ ელექტრონს საკმარისი ენერგია დაეგროვებინა კათოდიდან ამოსაფრენად. გათვლები უჩვენებენ, რომ ეს დრო წუთებით ან საათებით უნდა აღირიცხებიდეს. მაგრამ, გამოცდილება გვიჩვენებს, რომ ელექტრონები კათოდის განათებისთანავე მყისიერად გამოჩნდებიან. ამ მოდელის მიხედვით, ასევე გაუგებარი იყო ფოტოეფექტის წითეკი საზღვრის არსებობა. სინათლის ტალღურ თეორიას არ შეეძლო აეხსნა, თუ რატომ არ არის დამოკიდებული ფოტოელექტრონების ენერგია სინათლის ნაკადის ინტენსივობაზე და მისი მაქსიმალური კინეტიკური ენერგიისს სინათლის სიშირის პროპორციულობა.
ამგვარდ, სინათლის ელექტრომაგნიტურმა თეორიამ ვერ შეძლო ამ კანონზომიერებებია ახსნა.
გამოსავალი აინშტაინმა 1905 წელს იპოვა. ფოტოეფექტის კანონზომიერებები აინშტაინმა თეორიულად ახსნა პლანკის ჰიპოთეზის საფუძველზე, რომ სინათლე გამოსხივდება და შთაინთქმება გარკვეული პორციებით, და ყოველი პორციის ენერგია განისაზღვრება ფორმულით E = hν, სადაც h – პლანკის მუდმივაა. აინშტაინმა გადადგა შემდეგი ნაბიჯი ქვანტური ფიზიკის განვითარებაში. იგი მივიდა დასკვნამდე, რომ სინათლეს წყვეტილი (დისკრეტული) ბუნება აქვს. ელექტრომაგნიტური ტალღა შედგება ცალკეული პორციების - ქვანტებისაგან, რომლებსაც შემდგომში ფოტონები უწოდეს. ნივთიერებასთან ურთიერთქმედებებისას ფოტონი თავის ენერგიას hν სრულად გადასცემს ერთ-ერთ ელექტრონს. ამ ენერგიის ნაწილი ელექტრონს შეუძლია გაფანტოს ნივთიერების ატომებთან დაჯახებისას. ამის გარდა, ელექრონის ენერგიის ნაწილი იხარჯება მეტალი-ჰაერის საზღვარზე პოტენციური ბარიერის გადალახვისას. ამისთვის ელექტრონმა უნდა შეასრულოს გამოსვლის მუშაობა, რომელიც კათოდის მეტალის თვისებებზეა დამოკიდებული. უდიდესი კინეტიკური ენერგია, რომელიც კათოდიდან გამოფრენილ ფოტოელექტრონს შეიძლება ჰქონდეს, განისაზღვრება ენერგიის შენახვის კანონით:
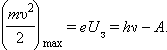
ამ ფორმულას ფოტოეფექტის აინშტაინის განტოლებას უწოდებენ.
აინშტაინის განტოლების საშუალებით შეიძლება აიხსნას გარე ფოტოეფექტის ყველა კანონზომიერება. ამ განტოლებიდან გამოდის მაქსიმალური კინეტიკური ენერგიის სიხშირეზე დამოკიდებულების წრფივობა და სინათლის ინტენსივიბისგან დამოუკიდებლობა, წითელი საზღვრის არსებობა, ფოტოეფექტის არაინერციულობა. ფოტოელექტრონების საერთო რცხვი, რომლებიც კათოდის ზედაპირს ერთ წამში ტოვებენ, პროპორციული უნდა იყოს იმ ფოტონების რიცხვისა, რომლებიც იგივე დრიში ხვდებიან ზედაპირს. აქდან გამოდის, რომ გაჯერების დენი სინათლის ნაკადის ინტენსივობის პირდაპირპროპორციული უნდა იყოს.
აინშტაინის განტოლების თანახმად, ჩამკეტი ძაბვის Uз სიხშირეზე ν დამოკიდებულების სწორის დახრის კუთხის ტანგენსი (ნახ. 3), ტოლია პლანკის h მუდმივას ელექტრონის e მუხტთან ფარდობისა:

ეს საშუალებას იძლევა ექსპერიმენტულად განისაზღვროს პლანკის მუდმივას მნიშვნელობა. ასეთი გაზომვები 1914 წელს მილიკენის მიერ იქნა შესრულებული და აღმოჩნდა კარგ თანხმობაში პლანკის მიერ ნაპოვნ მნიშვნელობასთან. ამ გაზომვებმა შესაძლებელი გახადეს ასევე გამოსვლის A მუშაობის განსაზღვრა:

სადაც c – სინათლის სიჩქარეა, λწ – ფოტოეფექტის წითელი საზღვრის შესაბამისი ტალღის სიგრძეა. მეტალების უმრავლესობისათვის გამოსვლი მუშაობა A რამოდენიმე ელექტრონ-ვოლტის ტოლია (1 ევ = 1,602·10–19 ჯ). ქვანტურ ფიზიკაში ელექტრონ-ვოლტი ხშირად გამოიყებენა ენერგიის საზომ ერTეულად. პლანკიs მუდმივას ელექტონ-ვოლტი.წამში გამისახული მნიშვნელობა, ტოლია
h = 4,136·10–15 ევ·წმ
მეტალებს შორის გამოსვლის ყველეზე მცირე მუშაობით ტუტე ელემენტები გამოირჩევიან. მაგალითად, ნატრიუმისათვის A = 1,9 ევ, რაც შეესაბამება წითერ საზღვარს λწ ≈ 680 ნმ. ამიტომ ფოტოელემენტების (ხილული სინათლის დასაფიქსირებელი მოწყობილობა) კათოდების დასამზადებლად ტუტეების ნაერთებს იყენებენ.
ამგვარად, ფოტოეფქტის კანონი ადასტურებს, რომ სინათლე გამოსხივებისა და შთანთქმის დროს ინ ნაწილაკების მსგავსად იცევა, რომლებმაც ფოტონების ან სინათლის ქვანტების სახელწოდება მიიღეს.
ფოტონის ენერგია ტოლია
E = hν.
ფოტონი ვაკუუმში c სიჩქარით მოძრაობს. ფოტონს მასა არ აქვს, m = 0. ფარდობითობის სპეციელური თეორიის ზოგადი თანაფარდობიდან, რომელიც ნაწილაკის ენერგიას, იმპულსს და მასას აკავშირებს,
E2 = m2c4 + p2c2,
გამოდის, რომ ფოტონს აქვს იმპულსი
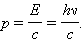
ამგვარად, სწავლებამ სინათლის შესახებ, შეასრულა ორი საუკუნის ხანგრძლივობის ბრუნი და კვლავ დაბრუნდა წარმოდგენამდე სინათლის ნაწილაკების - კორპოსკულების შესახებ.
მაგრამ ეს არ იყო ნიუტონის კორპუსკულების თეორიასთან მექანიკური დაბრუნება. XX საუკუნის დასაწყისში ნათელი გახდა, რომ სინათლეს ორმაგი ბუნება აქვს. გავრცელებისას სინათლე ავლენს ტალღურ ბუნებას (ინტერფერენცია, დიფრაქცია, პოლარიზაცია), ხოლო ნივთიერებებთან ურთიერთქმედებებისას - კორპუსკულურს (ფოტოეფექტი). სინათლის ამ ორმაგმა ბუნებამ კორპუსკულურ-ტალღური დუალიზმის სახელწოდება მიიღო. მოგვიანებით ორმაგი ბუნება აღმოაჩნდათ ელექტრონებს და სხვა ელემენტარულ ნაწილაკებს. კლასიკურ ფიზიკას არ შეუძლია მიკროობიექტების ტალღური და კორპოსკულური ბუნების კომბინაციის ნათელი მოდელის შექმნა. მიკროობიექტების მოძრაობა იმართება არა ნიუტონის კლასიკური მექანიკით, არამედ ქვანტური ფიზიკის კანონებით. პლანკის მიერ განვითარებული აბსოლუტურად შავი სხეულის გამოსხივების თეორია და ეინშტეინის ფოტოელექტრული ეფექტის თეორია თანამედროვე ფიზიკის საფუძველს წარმოადგენენ.
{loadnavigation}
წყაროს მიერ გამოსხივებულ სინათლეს თან მიაქვს ენერგია. სინათლის წყაროსთვის ენერგიის რესურსის მიწოდების მრავალი მექანიზმია არსებობს. იმ შემთხვევებში, როცა აუცილებელი ენერგია გათბობით გადაეცემა, ე.ი. სითბოს მიწოდებით, გამოსხივებას სითბურს ან ტემპერატურულს უწოდებენ. გამოსხივების ეს სახეობა XIX საუკუნის ფიზიკოსების განსაკუთრებულ ინტერეს იწვევდა, რადგანაც ყველა სხვა ლუმინესცენციის (ნათება) სახეობებისაგან განსხვავევით, სითბურ გამოსხივებას გახურებულ სხეულებთან შეუძლია თერმოდინამიკურ წონასწორობაში ყოფნა.
სხეულების სითბური გამოსხივების კანონზომიერებების შეაწავლისას, ფიზიკოსებს თერმოდინამიკასა და ოპტიკას შორის კავშირის დადგენის იმედი ჰქონდათ.
თუ სარკულად შემოსაზღვრულ ჩაკეტილ სიღრუეში სხვდასხვა ტემპერატურამდე გახურებულ რამოდენიმე სხეულს მოვათავსებთ, მაშინ, როგორც გამოცდილება გვიჩვენებს, ასეთი სისტემა რაღაც დროის განმავლობში სითბურ წონასწორობის მდგომარეობამდე მივა, რომლის დროსაც ყველა სხეული ერთნაერ ტემპერატურას იძენს. სხეულები ენერგიას მხოლოდ სხივური ენერგიის გამოსხივებითა და შთანთქმით ცვლიან. წონასწორობის პროცესში ყოველი სხეულის მიერ ენერგიის გამოსხივებისა და შთანთქმის პროცესები საშუალოდ აწონასწორებს ერთმანეთს და სხეულებს შორის სივრცეში ენერგიის სიმკვრივე აღწევს გარკვეულ მნიშვნელობას, რომელიც მხოლოდ დამყარებულ ტემპერატურაზეა დამოკიდებული. გარკვეული ტემპერატურის მქონე სხეულებთან თერმოდინამიკურ წონასწორობაში მყოფ ამ გამოსხივებას წონასწორულ ან შავ გამოსხივებას უწოდებენ. წონასწორული გამოსხივების სიმკვრივე და მისი სპეტრული შედგენილობა მხოლოდ ტემპერატურაზეა დამოკიდებული.
თუ მცირე ნახვრეტის საშუალებით შევიხედავთ სიღრუეში, რომელშიც გამოსხივებასა და გახურებულ სხეულებს შორი თერმოდინამიკური წონასწორობაა დამყარებული, თვალი ვერ გაარჩევს სხეულების მოყვანილობებს და დააფიქსირებს მხოლოდ მთელ სიღრუეში ერთგვაროვან ნათებას.
ვთქვათ სიღრუეში მყოფ ერთ სხეულს ახასიათებს მასზე დაცემული ნებისმიერი სპექტრული შემადგენლობის მთელი სხივური ენერგიის შთანთქმის თვისება. ასეთ სხეულს აბსოლუტურად შავს უწოდებენ. გარკვეული ტემპერატურისას გამოსხივებასთან სითბურ წონასწორობაში მყოფი აბსოლუტურად შავი სხეულის საკუთარ სითბურ გამოსხივებას იგივე სპექტრული შედგენოლობა უნდა ჰქონდეს რაც მის გარმომცველ წონასწორულ გამოსხივებას. წინააღმდეგ შემთხვევაში წონასწორობა აბსილუტურად შავ სხეულსა და მის გარემომცველ გამოსხივებას შორის ვერ დამყარდებოდა. ამიტომ ამოცანა დადის აბსოლუტურად შავი სხეულის სპექტრული გამოსხივების შესწავლასთან. კლასიკურმა ფიზიკამ ამ ამოცანის გადაწყვეტა ვერ შეძლო.
სიღრუეში წონასწორობის დამყარებისათვის აიცილებელია, რომ ყოველი სხეული მხოლოს იმდენ სხივურ ენერგიას ასხივებდეს, რამდენის შთანთქა. ეს სითბური გამოსხივების ერთ-ერთი უმნიშვნელივანესი კანონზომიერებაა. აქედან გამომდინარეომს, რომ მოცემული ტამპერატურის შემთხვევაში აბსოლუტურად შავი სხეული ზედაპირის ფართობის ერთეულიდან დროის ერთეულში ნებისმიერ სხვა სხეულზე მეტ სხივურ ენერგიას ასხივებს.

ნახ. 1.
აბსოლუტურად შავი სხეული
აბსოლუტურად შავი სხეულები ბუნებაში არ არსებობენ. ასეთი სხეულის კარგ მოდელს ჩაკეტილ სიღრუეში ნახვრეტი წარმოადგენს (ნახ. 1). ნახვრეტიდან სიღრუეში მოხვედრილი სინათლე მრავალრიცხოვანი არეკვლის შემდეგ თითქმის მთლიანად შთაინთქმება კედლების მიერ, და ნახვრეტი გარედან სრულიად შავად გამოჩნდენა. მაგრამ, თუ სიღრუე გაცხელებულია გარკვეულ T ტტმპერატურამდე, და შიგნით კი დამყარდა სითბური წონასწორობა, ნახვრეტიდან გამოსული გამოსხივება აბსოლუტურად შავი სხეულის გამოსხივება იქნება. სითბური გამოსხივების შემსწავლელ ყველა ექსპერიმენტში სწორედ ასე ხდება აბსოლუტურად შავი სხეულის მოდელირება.
სიღრუის შიგნით ტემპერატურის ზრდით ნახვრეტიდან გამოსული გამოსხივების ენერგიაც იზრდება და იცვლება სპექტრული შედგენილობა.
მოცემული T ტემპერატურისათვის აბსოლუტურად შავი სხეულის გამოსხივებაში ენერგიის ტალღის სიგრძეების მიხედვით განაწილება ხასიათდება გამოსხივების უნარით r (λ, T), რომელიც სხეულის ზედაპირის ფართობის ერთეულიდან ტალღის სიგრძეთა ერთეულ ინტერვალში გამოხსვების სიმძლავრის ტოლია. ნამრავლი r (λ, T) Δλ ერთეულოვანი ზედაპირის მიერ ყველა მიმართულებით ტალღის სიგრძეთა Δλ ინტერვალში გამოსხივების სიმძლავრის ტოლია. ანალოგიურად შეიძლება ენერგიის სიხშირეების მიხედვით განაწილების r (ν, T) შემოტანა. ფუნქციას r (λ, T) (ან r (ν, T)) ხშირად სპექტრულ ნათებას უწოდებენ, ხოლო ყველა ტალღის სიგრძის მიერ გამოსხივებულ R (T) სრულ ნაკადს, რომელიც ტოლია

ინტეგრალურ ნათებას უწოდებენ.
XIX საუკუნის ბოლოს აბსოლუტურად შავი სხეულის გამოსხივება ექსპერიმენტულად კარგად იყო შესწავლილი.
1879 წელს იოზეფ სტეფანმა ექსპერიმენტული მონაცემების ანალიზის სიფუძველზე დაასკვნა, რომ აბსოლუტურად შავი სხეულის ინტეგრალური ნათება R (T) აბსოლუტური T ტემპერატურის მეოთხე ხარისხის პროპორციულია:
R (T) = σT4.
ცოდა მოგვიანებით, 1884 წელს ბოლცმანმა ეს დამოკიდებულება თერმოდინამიკურ მოსაზრებებზე დაყრდნობით თეორიოლად გამოიყვანა. ამ კანონმა სტეფან-ბოლცმანის კანონის სახელწოდება მიიღო. σ მუდმივას რიცხვითი მნიშვნელობა, თანამედროვე გაზომვების მიხედვით, ტოლია
σ = 5,671·10–8 Вт / (м2 · К4).
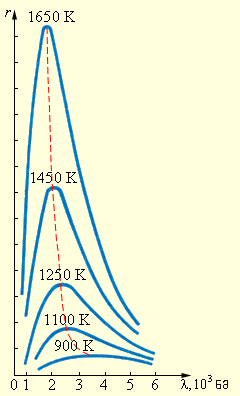
ნახ. 2.
სხვადასხვა ტემპერატურისათვის აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილება r (λ, T)
XIX საუკინის 90-იან წლებში შესრულდა აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების ზედმიწევნით ფაქიზი ექსპერიმენტული გაზომვები, რომლებმაც აჩვენეს, რომ ტემპერატურის ყოველი T მნიშვნელობისთვის r (λ, T) დამოკიდებულებას მკვეთრად გამოსახული მაქსიმუმი აქვს (ნახ. 2). ტემპერატურის ზრდით მაქსიმუმი მოკლე ტალღის სიგრძეებისკენ ინაცვლებს, ამასთან მაქსიმუმის შესაბამისი ტემპერატურისა და ტალღის სირძის ნამრავლი მუმივი რჩება:
λmT = b ან λm = b / T.
ეს დამოკიდებულება ადრე ვინისვინის მიერ იყო მიღებილი თერმოდინამიკიდან. იგი ე.წ. ვინის წანაცვლების კანონს გამოსახავს: ტალღის სიგრძე λm, რომელიც აბსოლუტურად შავი სხეულის გამოსხივების მაქსიმუმი მოდის, აბსოლუტური ტემპერატურის T უკუპროპორციულია. ვინის მუდმივას მნიშვნელობაა
b = 2,898·10–3 მ·К.
ლაბორატორიულ პირობებში პრაქტულულად მიღწევადი ტემპერატურებისთვის გამოსხივების უნარის მაქსიმუმი r (λ, T) ინფრაწითელ უბანში მდებარეობს. მხილოდ როცა T ≥ 5·103 К- შსემთხვევაში მაქსიმუმი ხილულ სპექტრულ უბანში ხვდება. მზის გამოსხივების ენერგიის მაქსიმუმი დაახლოებით 470 ნმ-ზე (სპექტრის მწვანე უბანი) მოდის, რაც მზის გარე ფენის ტემპერატურას დაახლოებით 6200 К-ს შეესაბამება (თუ მზეს აბსოლუტურად შავი სხეულად განვიხილავთ).
სტეფან-ბოლცმანისა და ვინის კანონების თეორიული გზით გამოყვანაში თერმოდინამიკის წარმატებამ იმედე გააჩინა, რომ თერმოდინამიკური მოსაზრებების გამოყენებით შესაძლებელი იქნებიდა აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების ყველა მრუდის r(λ, T) მიღება. 1900 წელს ამ პრობლემის გადაჭრას ცნიბილი ინგლისელი ფიზიკოსი ჯ.რელეი ცდილობდა, რომელიც თავის მსჯელობების საფუძველად იყენებდა კლასიკური სტატისტიკის თეორემას თერმოდინამიკური წონასწორობისას ენერგიის თავისუფლების ხარისხების მიხედვით თანაბარი განაწილების შესახებ. ეს თეორემა რელეიმ სიღრუეში წონასწორული მდგომარეობის პირობებში გამოიყენა. მოგვიანებით ეს იდეა დაწვრილებით განავითარა ჯინსმა. ამგვარად გახდა შესაძლებელი აბსოლუტურად შავი სხეულის გამოსხივების უნარის ტალღის სიგრძესა λ და ტემპერატურაზე T დამოკიდებულებისმიღება:
r (λ, T) = 8πkTλ–4.
ამ თანაფარდობას რელეი-ჯინსის ფორმულას უწოდებენ. იგი ექსპერიმენტულ მონაცემებთან მხოლოს საკმარისად გრძელი ტალღებისათვისაა თანხმობაში (ნახ. 3). ამის გარდა, ამ ფორმულიდან გამოდის აბსურდული დასკვნა იმის შესახებ, რომ აბსოლუტურად შავი სხეულის ინტეგრალური ნათობა R (T) უნდა უსასრულო ხდებოდეს, ხოლო, აქედან გამომდინარე, გახურებულ სხეულსა და ჩაკეტილი სიღრუის გამოსხივებას შორის წონასწორობა შეიძლება მხოლოდ ტემპერატურის აბსოლუტური ნულის დროს დამყარდეს.

ნახ. 3.
აბსოლუტურად შავი სხეულის გამოსხივების ტალღის სიგრძეების მიხედვით ენერგიის განაწილების r (λ, T) შედარება რელეი-ჯინსის ფორმულასთან T = 1600 К-სათვის
ამგვარად, კლასიკური ფიზიკის თვალსაზრისით უნაკლო დასკვნას მივყავართ ფომულამდე, რომელიც ცდებს მკვეთრად ეწინააღმდეგება. ნათელი გახდა, რომ აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების შესახებ ამოცანის გადაჭრა არსებული თეორიის პირობებში შეუძლებელი იყო. ეს ამოცანა მ.პლანკმა წარმატებით გადაწყვიტა კლასიკური ფიზიკისათვის უცხო, ახალი იდეის დახმარებით.
პლანკი მივიდა დასკვნამდე, რომ გახურებული სხეულის მიერ ელექტრომაგნიტური ენერგიის გამოსხივებისა და შთანთქმის პროცესები უწვეტად კი არ მიმდინარეობს, რორც კლასიკურ ფიზიკაში იყო მიღებული, არამედ სასრული პორციების - ქვანტების სახით. ქვანტი სხეულის მიერ გამოსხივებული ან შთანთქმული ენერგიის მინიმალური პორციაა. პლანკის თეორიის მიხედვით ქვანტის ენერგია E სინათლის სიხშირის პირდაპირპროპორციულია:
E = hν,
სადაც h – ე.წ. პლანკის მუდმივაა. h = 6,626·10–34 ჯ·წმ. პლანკის მუდმივა უნივერასლური კონსტანტაა, რომელიც ქვანტურ ფიზიკაში იგივე როლს ასრულებს, რასაც სინათლის სიჩქარე ფარდობითობის სპეციალურ თეორიაში.
ელექტრომაგნიტური გამოსხივების გამოსხივებისა და შთანთქმის პროცესები წყვეტილი ხასიათის შესახებ ჰიპითეზის საფუძველზე პლანკმა მიიღო ფორმულა აბსოლუტურად შავი სხეულის სპექტრული ნათობისათვის. პლანკის ფორმულა მოსახერხებელია ჩაიწეროს ისეთი ფორმით, როცა აბსოლუტურად შავი სხეულის გამოსხივების ენერგიის განაწილება სპექტრში გამოსახულია სიხშირით ν, და არა ტალღის სიგრძით λ.
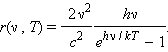
სადაც c – სინათლის სიჩქარე, h – პლანკის მუდმივა, k – ბოლცმანის მუდმივა, T – აბსოლუტური ტემპერატურაა.
პლანკის ფორმულა კარგად აღწერს აბსოლუტურად შავი სხეულის გამოსხივების სპექტრულ განაწილებას ნებისმიერი სიხშირისათვის. ის კარგ თანხმობაშია ექსპერიმენტულ მონაცემებთან. პლანკის ფორმულიდან შეიძლება სტეფან-ბოლცმანის და ვინის კანონების გამოყვანა. როცა hν << kT პლანლის ფორმულა რელეი-ჯინსის ფორმულაში გადადის.
შავი სხეულის გამოსხივების პრობლემის გადაჭრა ფიზიკაში ახალი ეპოქის დაწყებით აღინიშნა. ადვილი არ იყო კლასიკურ ფიზიკაზე უარის თქმა, თითონ პლანკიც კი, მისივე უდიდესი აღმოჩენის შემდეგაც, რამოდენიმე წლის განმავლობაში უშედეგოდ ცდილობდა ენერგიის დაქვანტვის კლასიკური ფიზიკის თვალსაზრისიდან ახსნას.
{loadnavigation}
2000 წლის დეკემბერში მსოფლიო სამეცნიერო საზოგადოებრიობამ აღნიშნა ახალი მეცნიერების - ქვანტური ფიზიკის - ასი წლის იუბილე და ახალი ფუნდამენტური ფიზიკური კონსტანტის - პლანკის მუდმივის აღმოჩენა. ამაში დამსახურება გამოჩენილ გერმანელ ფიზიკოსს მაქს პლანკს მიუძღვის. მან შესძლო გადაეჭრა გახურებული სხეულების მიერ გამოსხივებული სინათლის სპექტრული განაწილების პრობლემა, რომლის წინაშეც კლასიკური ფიზიკა უძლური აღმოჩნდა. პლანკმა პირველმა გამოთქვა, კლასიკურ ფიზიკასთან შეუთავსებელი, ჰიპოთეზა ოსცილატორის (რხევითი სისტემის) ენერგიის დაქვანტვის შესახებ. სწორედ ამ ჰოპოთეზამ, რომელის შემდგომში მრავალი ცნიბილი ფიზიკოსის შრომით განვითარდა, მისცა ბიძგი ძველი ტარდიციების გადახედვისა და მსხვრევის პროცესს, რაც ქვანტური ფიზიკის შექმნით დასრულდა.
