{loadnavigation}
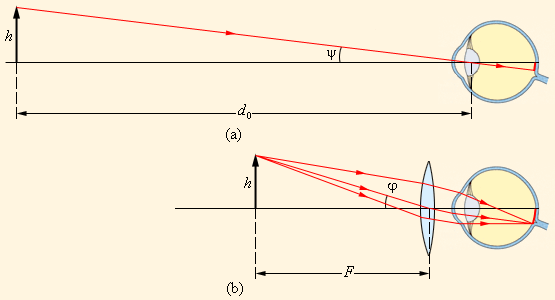
შეუიარაღებული თვალისთვის უმცირესი მხედველობის კუთხე დაალოებით 1'-ს ტოლია. ეს კუთხე ბადურის მოზაიკური აგებულებით, და ასევე სინათლის ტალღური თვისებებით განისაზღვრება. არსებობს მხედბელობის კუთხის გასადიდებელი ხელსაწყოები - ლუპა, მიკროსკოპი, , ტელესკოპი. ვიზუალური დაკვირვებებისას თვალი ოპტიკური სისტემის განუყოფელ ნაწილს წარმოადგენს, ამიტომ თვალის აღმჭურველ ხელსაწყოებში სხივთა სვლა თვალის აკომოდაციაზეა დამოკიდებული. ვიზუალური დაკვირვების ოპტიკური ხელსაწყოების მუშაობის ანალიზისას ყველაზე ხელსაყრელია ჩაითვალოს, რომ თვალი აკომოდირებილია უსასრულობაზე. ეს ნიშნავს, რომ საგნის ყოველი წერტილიდან მომავალი სხივები, ხელსაწყობში გაივლის და პარალელური კონის სახით თვალში ხვდება. ამ პირობებში წრფივი გადიდების ცნება აზრს კარგავს. ოპტიკური ხელსაწყოთი საგნის დაკვირვებისას მხედველობის φ კუთხის ფარდობას შეუიარაღებელი თვალით დაკვირვებისას მხედველობის ψ კუთხესთან კუთხური გადიდებას უწოდებენ:
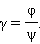
კუთხური გადიდება ვიზუალური დაკვირვების ოპტიკური ხელსაწყოს მნიშვნელოვანი მახასიათებელია.
უნდა აღინიშნოს, რომ ზოგ სახელმძღვანელოში ჩათვლილია, რომ დამკვირვებლის თვალი აკომოდირებულია ნორმალური თვალის საუკეთესო მხედველობის d0 მანძილზე. ამ შემთხვევაში ხელსაწყოში სხივთა სვლა რამდენადმე რთულდება, მაგრამ ხელსაწყოს კუთხური გადიდება დაახლოებით ისეთივე რჩება, როგორიც უასასრულობაზე აკომოდაციისას.
ლუპა. ვიზუალური დაკვირვების უმარტივეს ხელსაწყოს ლუპა წარმოადგენს. ლუპას მცირე ფოკუსური მანძილის (F ≈ 10 სმ) მქონე შემკრებ ლინზას უწოდებენ. ლუპას თვალის ახლოს ათავსებენ, ხოლო დასათვალიერებელ საგანს მის ფოკალურ სიბრტყეში. საგანი ლუპაში ჩანს 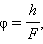 კუთხით, სადაც h – საგნის ზომაა. იგივე საგნის შეუიარაღებელი თვალით დათვალიერებისას იგი ნორმალური თვალის საუკეთესო მხედველობის მანძილზე d0 = 25 სმ-ზე უნდა მოთავსდეს. საგანი გამოჩნდება
კუთხით, სადაც h – საგნის ზომაა. იგივე საგნის შეუიარაღებელი თვალით დათვალიერებისას იგი ნორმალური თვალის საუკეთესო მხედველობის მანძილზე d0 = 25 სმ-ზე უნდა მოთავსდეს. საგანი გამოჩნდება
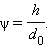 კუთხით.
კუთხით.
აქედან გამოდის, რომ ლუპის კუთხური გადიდება ტოლია
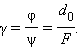
10სმ ფოკუსური მანძილის მქონე ლინზა 2,5-ჯერ გადიდებას იძლევა. ლუპის მუშაობა ნახ. 1-ზეა ნაჩვენები.
ნახ. 1.
ლუპის მოქმედება: а – საგნის დათვალიერება შეუიარაღებელი თვალით ხდენა ნორმალური თვალის საუკეთესო მხედველობის მანძილზე d0 = 25 სმ ; b –საგნის დათვალიერება F ფოკუსური მანძილი მქონე ლუპით ხდება
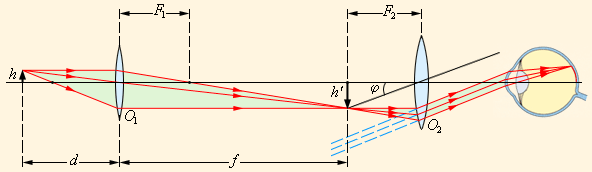
მიკროსკოპი. მიკრისკოპი პატარა საგნების დაკვირვებისას დიდi გადიდების მისაღებად გამოიყენება. სხეულის გამოსახულების მიკროსკოპით გადიდება ისეთი ოპტიკური სისტემის გამოyენებით მიიღწევა, რომელიც მოკლეფოკუსიანი ლინზის - O1 ობიექტივისა და O2 ოკულარისაგან შედგება (ნახ. 2). ობიექტივი საგნის გამოსახულების პირდაპირ გადაბრუნებულ გამოსახულებას იძლება. ამ შუალედურ გამოსახულებას თვალი ოკულარის საშუალებით ათვალიერებს, რომელიც ლუპის ანალოგიურად მოქმედებს. ოკულარი ისეა განლაგებული, რომ შვალედური გამოსახულება მის ფოკალურ სიბრტყეში ხვდებოდეს; ასეთ შემთხვევაში საგნის ყოველი წერტილიდან მომავალი სხივები ოკულარის შემდეგ პარალელურ კონად ვრცელდება.
ნახ. 2.
სხივთა სვლა მიკროსკოპში
ოკულარში დანახული საგნის წარმოსახვითი გამოსახულება გადაბრუნებულია. თუ ეს მოუხერხებელი აღმოჩნდება (მაგალითად, წვრილი შრიფტის წაკითხვისას), ობიექტივის წინ თვითონ საგნის გადაბრუნება შეიძლება. ამიტომაც მოკროსკოპის კუთხური გადიდება, მიღებულია, ჩაითვალოს დადებითად.
როგორც ნახ. 2-დან ჩანს, ოკულარში დანახული საგნის ხედვის φ კუთხე მცირე კუთხეების მიახლოებაში
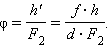
დაახლოებით შეიძლება ჩაითვალოს, რომ d ≈ F1 და f ≈ l, სადაც l –მიკრისკოპის ობიექტივსა და ოკულარს შორის მანძილია („მილის სიგრძე“). იგივე საგნის შეუიარაღებელი თალის დათვალიერებისას
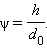
საბოლოოდ მიკროსკოპით საგნის γ კუთხური გადიდების ფორმულა ღებულობს სახეს
კარგ მიკროსკოპს შეუძლია რამოდენიმე ასეულჯერ გადიდება. დიდ გადიდებებისას თავს იჩენს დიფრაქციის მოვლენა.
რეალურ მიკროსკოპებში ობიექტივი და ოკულარი რთულ ოპტიკურ სისტემებს წარმოადგენენ, რომლებშიც სხვადასხვა აბერაციები თავიდანაა აცილებული.
ტელესკოპი. ტელესკოპები დაშორებული საგნების დაკვირვებისთვისაა გამკუთვნილი. ისინი ორი ლინზისაგან შედგებიან ; საგნის მხარეს მიმათული დიდი ფოკუსური მანძილის მქონე ლინზა (ობიექტივი) და დამკვირვებლის მხარეს, მცირე ფოკუსური მანძილის მქონე ლინზა (ოკულარი). ტელესკოპები ორი სახისაა:
- კეპლერის ტელეკოპი (მილი), რომელიც ასტრონომიული დაკვირვებებისთვისაა განკუთვნილი. იგი იძლევა დაშორებული საგნების გადიდებულ გადაბრუნებულ გამოსახულებას და ამიტომ მოუხერხებელია დედამიწაზე არსებული საგნების დაკვირვებებისთვის;
- გალილეის ტელესკოპი (მილი), რომელიც დედამიწაზე დაკვირვებებისათვისაა განკუთვნილი. იგი გადიდებულ და პირდაპირ გამოსახულებას იძლევა. გალილეის მილში ოკულარად გამბნევი ლინზაა გამოყენებული.
ნახ. 3-ზე ასტრონომიულ ტელესკოპში სხივთა სვლაა გამოსახული. ითვლება, რომ დამკვირვებლის თვალი უსასრულობაზეა აკომოდირებული, ამიტომ დაშორენული საგნის ნებისმიერი წერტილიდან მომავალი სხივი ოკულარის მერე პარალელურად კონის სახით გამოდის. სხივთა ასეთ სვლას ტელესკოპურს უწოდებენ. ასტრონომიულ მილში სხივთა ტელესკოპური სვლა მიიღწევა, თუ დაცულია პირობა: მანძილი ობიექტივსა და ოკულარს შორის მათი ფიკუსური მანძილების ჯამის ტოლია l = F1 + F2.
ტელესკოპს γ კუთხური გადიდებით ახასიათებენ. მიკროსკოპისგან განსხვავებით, ტელესკოპით დაკვირვებული საგნები დამკვივებლისგან ყოველთვის დაშორებულნი არიან. თუ დაშორებული საგანი შეუიარაღებელი თვალით ψ კუთხით ჩანს, ხოლო ტელესკოპის საშუალებით φ კუთხით, მაშინ კუთხურ გადიდებას უწოდებენ ფარდობას
γ კუთხურ გადიდებას, წრფივი Γ გადიდების მსგავსად, შეიძლება მივუწეროთ ნიშნები პლიუსი და მინუსი, იმის მიხედვით, გამოსახულება პირდაპირია თუ გადაბრუნებული. კეპლერის ასტრონომიული მილის კუთხური გადიდება უარყოფითია, ხოლო გალილეის მილისა კი დადებითი.
ტელესკოპების კუთხური გადიდება ფოკუსირი მანძილების საშუალებით ასე გამოისახება:


ნახ. 3.
სხივთა სვლა ტელესკოპში
ობიექტივებად დიდ ასტრონომიულ ტელესკოპებში ლინზის ნაცვლად სფერული სარკეები გამოიყენება. ასეთ ტელესკოპებს რეფლექტორებს უწოდებენ (ლინზიანებს რაფრაქტირები ეწოდებათ). კარგი სარკის დამზადება უფრო ადვილია და თან, სარკეს , ლინზებისგან განსხვავებით ქრომატული აბერაცია არ ახასიათებს.
უნდა აღინშნოს, რო დიდი ასტრონომიული ტელესკოპები განკუთვნილია არა მარტო დამკვირვებელსა და კოსმოსურ ობიექტს შორის კუთხირი მანძილის გასადიდებლად, არამედ სუსტი მნათი ობიექტებიდან მომავალი სინათლის ენერგიის ნაკადის გასაძლიერებლად.
{loadnavigation}
ადამიანის თვალი რთულ ოპტიკურ სისტემას წარმოადგენს, რომელიც თავისი მოქმედებით ფოტოაპარატის ანალოგიურია. თვალის სქემატური აგებულება ნახ. 1-ზეა მოცემული. თვალს თითქმის ბურთულის ფორმა აქვს და დიამეტრით დაახლოებით 2,5 სმ-ია. გარედან ის თეთრი ფერის დამცავი გარსით 1 - სკლერითაა დაფარული. სკლერის წინა გამჭვირვალე ნაწილს 2 რქოვანა ეწოდება. მისგან გარკვეულ მანძილზე პიმენტით შეფერილი ფერადი გარსია 3. ფერად გარსში მოთავსებული ხვრელი გუგას წარმოადგენს. დაცემული სინათლის ინტენსივობაზე დამოკიდებულებით გუგა რეფლექსურად იცვლის დიამეტრს დაახლოების 2-დან 8 მმ-მდე, ე.ი. ფოტოაპარატის დიაფრაგმასავით მოქმედებს. რქოვანასა და ფერად გარსს შორის გამჭვირვალე სითხეა. გუგის უკან ბროლი 4 - ლინზისმაგვარი ელასტიური სხეული მდებარეობს. სპეციალური კუნთი 5 გარკვეულ საზღვრებში ცვლის ბროლის ფორმას, რის შედეგადაც მისი ოპტიკური ძალა იცვლება. თვალის დანარჩენი ნაწილი მინისებური სხეულითაა შევსებული. თვალის უკანა ნაწილი - თვალის ფსკერი, დაფარულია ბადურისებური გარსით 6, რომელის მხედველობითი ნერვის 7 რთულ განშტოებას წარმოადგენს, ნერვული დაბოლოებებით - სინათლისმგრძნობიარე ელემენტებით, ჩხირიბითა და კოლბებით.
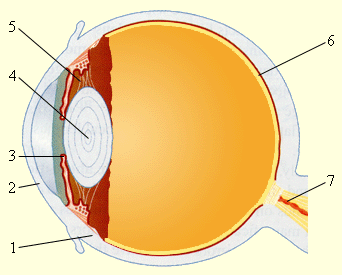
ნახ. 1.
ადამიანის თვალი
საგნიდან მომავალი სხივი ჰაერი-რქოვანას საზღვარზე გარდატყდება და გაივლის ბროლს (ცვლადი ოპტიკური ძალის მქონე ლინზა) და ქმნის გამოსახულიბას ბადურაზე.
რქოვანა, გამჭირვალე სითხე, ბროლი და მინისებური სხეული ქმნიან ოპტიკურ სისტემას, რომლის ოპტიკური ცენტრი რქოვანადან 5 მმ მანძილზე მდებარეობს. თვალის კუნთის მოდუნების შემთხვევაში თვალის ოპტიკური ძალა დაახლოებით 59 დიოპტრია, ხოლო კუნთის მაქსიმალური დაძაბვისას 70 დიოპტრი.
თვალის, როგორც ოპტიკური ხელსაწყოს ძირითადი თავისებურება საგნის დაშორებაზე დამიკიდებული თვალის ოპტიკის ოპტიკური ძალის რეფლექსური ცვლილებაა. თვალის ამ თვისებას აკომოდაცია ეწოდება.
თვალის აკომოდაციის არე ორი წერტილის მდებარეობის მიხედვით შეიძლება განსაზღვროს:
- აკომოდაციის შორეული წერტილი განისაზღვრება საგნის მდებარეობით, რომლის გამოსახულებაც მიიღება ბადურაზე თვალის მოდუნებული კუნთის საშუალებით. ნორმალური თვალისთვის აკომოდაციის შორეული წერტილი უსასრულობაში მდებარეობს.
- აკომოდაციის ახლო წერტილი - მანძილი დასაკვირვებელ საგანსა და თვალს შორის თვალის კუნთის მაქსიმალირი დაძაბვისას. ახლო წერტილი ნირმალური თვალისთვის თვალიდან 10-20 სმ მანძილზე მდებარეობს. ასაკთან ერთად ეს მანძილი იძრდება.
თვალის აკომოდაციის არის გამსაზღვრელი ამ ორი წერტილის გარდა თვალს აქვს საუკეთესო მხედველობის მანძილი, ე.ი. მანძილი საგნიდან თვალამდე, რომელზეც ყველაზე მოსახერხებელია (ზედმეტი დაძაბვის გარეშე) საგნის დეტალების დათვალიერება (მაგალითად, წვრილი შრიფტის წაკითხვა). ნორმალური თვალისათვის ეს მანძილი 25 სმ-ა.
მხედველობის დარღვევის შემთხვევეში დაშორებული საგნების გამოსახულება თვალის დაძაბვისას შეიძლება ან ბადურის წინ (ახლომხედველობა), ან ბადურის უკან (შორსმხედველობა) აღმოჩნდეს (ნახ. 2).
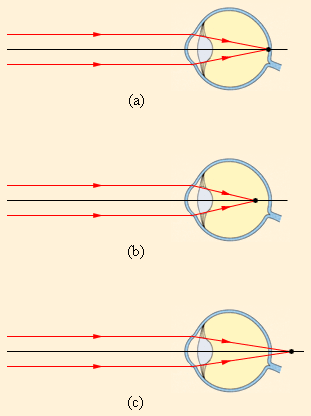
ნახ. 2.
დაშორებული საგნის გამოსახულება თვალში: a – ნორმალური თვალი; b – ახლომხედველი თვალი; с – შორსმხედველი თვალი
საუკეთესი მხედველობის მანძილი, ახლომხედველი თვალისთვის ნაკლებია, ხოლო შორსმხედველისათვის უფრო მეტია, ნორმალურ თვალთან შედარებით. მხედველობის დეფექტის გასასწორებლად სათვალეები გამოიყენება. შორსმხედველი თვალისთვის აუცილებელია სათვალე დადებითი ოპტიკური ძალით (შემკრები ლინზა), ხოლო ახლომხედველისათვის - უარყოფითი ოპტუკური ძალით (გამბნევი ლინზა).
დაშორებული საგნების დაკვირვებისთვის ლინზების ოპტიკური ძალა უნდა იყო ისეთი, რომ პარალელური სხივები თვალის ბადურაზე ფოკუსირდებოდნენ. თვალი სათვალის საშუალებით უნდა ხედავდეს დაშორებული საგნის პირდაპირ წარმოსახვით გამოსახულებას მოცემული თვალის აკომოდაციის შორეულ წერტილში. თუ, მაგალითად, თუ ახლომხედველი თვალის აკომოდაციის შორეულ წერტილი 80 სმ მანძილზე მდებარეობს, თხელი ლინზის ფორმულის გამოყენებით მივიღებთ:
d = ∞, f = –0,8 მ, აქედან გამომდინარე, 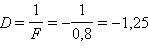 დიოპტრი
დიოპტრი
უნდა აღინიშნოს, რომ შორსმხედველი თვალისთვის აკომოდაციის შორეულ წერტილი წარმოსახვითია, ე.ი. დაუძაბავი თვალი ბადურაზე აფოკუსებს სხივთა კრებად კონას. ამიტომ დაშორებული საგნების დათვალიერებისთვის სათვალემ შორსმხედველი თვალისთვის პარალელური სხივები კრებად კონად უნადა გადააქციოს, ე.ი. უნდა გააჩნდეს დადებითი ოპტიკური ძალა.
ახლომხედველობის სათვალემ (მაგალითად, საკითხავმა) უნდა შექმნას d0 = 25 სმ მანძილზე (ე.ი. ნორმალური თვალისათვის მხეველობის საუკეთესო მანძილზე) მდებარე საგნის წარმოსახვითი გამოსახულება, მოცემული თვალისთვის საუკეთესო მანძილზე. ვთქვათ, მაგალითად, ახლომხედველი თვალისთვის მხეველობის საუკეთესო მანძილი 16 სმ-ია. თხელი ლინზის ფორმულის გამოყენებით მივიღებთ: d = d0 = 0,25 м, f = –0,16 м, აქედან გამომდინარე, 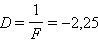 დიოპტრი. აქედან გამომდინარე, ადამიანის აკომოდაციის არის შეზღუდვის შემთხვევეში ახლოს დასანახ სათვალეს უნდა ჰქონდეს მეტი (მოდულით) ოპტიკური ძალა, ვიდრე შორს მყოფი საგნების დასათვალიერბელ სათვალეს.
დიოპტრი. აქედან გამომდინარე, ადამიანის აკომოდაციის არის შეზღუდვის შემთხვევეში ახლოს დასანახ სათვალეს უნდა ჰქონდეს მეტი (მოდულით) ოპტიკური ძალა, ვიდრე შორს მყოფი საგნების დასათვალიერბელ სათვალეს.
ნახ. 3-ზე მოცემულია შორსმხედველობისა და ახლომხედველობის კორექცია სათვალის საშუალებით.
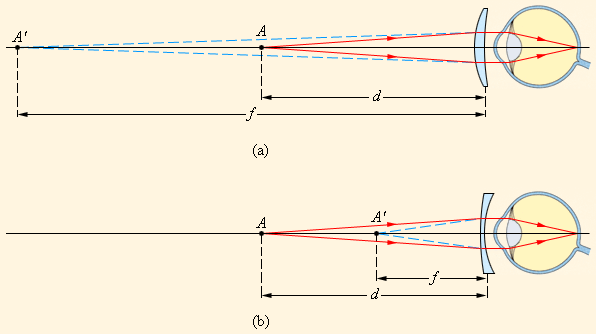
ნახ. 3.
საკითხავი სათვალის შერჩევა შორსმხედველი (a) და ახლომხედველი (b) თვალისთვის. ნორმალური თვალის საუკეთესო მხედველობისთვის A საგანი d = d0 = 25 см მანძლიზე უნდა მდებარეობდეს. წარმოსახვითი A' გამოსახულიბა მოცემული თვალისათვის საუკეთესი f მანძილზეა მოთავსებული
{loadnavigation}
ლინზას ორი სფერული ზედაპირით შემოსაზღვრულ გამჭვირვალე სხეულს უწოდებენ. თუ მისი სისქე მცირეა სფერული ზედაპირების სიმრუდის რადიუსთან შდარებით, მაშინ ლინზას თხელს უწოდებენ.
ლინზები პრაქტიკულად ყველა ოპტიკური ხელსაწყოს შემადგენმომაში შედიან. არსებობს შემკრები და გამბნევი ლინზები. შემკრები ლინზა შუაში უფრო სქელია ვიდრე კიდეებზე, გამბნევი კი პირიქით, შუაშია უფრო თხელი (ნახ. 1).

ნახ. 1.
შემკრები (a) და გამბნევი (b) ლინზები და მათი პირობითი აღნიშვნა
სწორს, რომელიც სიმრუდის O1 და O2 ცენტრებზე გადის, ლინზის მთავარი ოპტიკური ღერძი ეწოდება. თხელი ლინზის შემთხვევაში მიახლოებით შეიძლება ჩავთვალოთ, რომ მთავარი ოპტიკური ღერძი ლინზასთან მხოლოდ ერთ O წერტილში იკვეთება, რომელსაც ლინზის ოპტიკურ ცენტრს უწოდებენ. სინათლის სხივი ოპტიკუტ ცენტრზე გავლისას არ გადაიხრება საწყისი მიმართულებიდან. ოპტიკურ ცენტრზე გამავალი ყველა სწორს გვერდითი ოპტიკური ღერძები ეწოდება.
თუ ლინზაზე მთავარი ოპტიკური ღერძის სხივთა პარალელურ კონას მივმართავთ, ლინზაში გავლის შემდეგ სხივები (ან მათი გაგრძელებები) შეიკრიბებიან ერთ F წერტილში, რომელსაც ლინზის მთავარ ფოკუსს უწოდებენ. თხელ ლინზებს ორი მთავარი ფოკუსი აქვთ, რომლებით ლინზის ღერძის სიმეტრიულად არიან განლაგებული. შემკრები ლინზის ფოკუსი ნამდვილია, გამბნევისა კი - წარმოსახვითი. ერთ-ერთი გვერდითი ოპტიკური ღერძის პარალელური სხივთა კონა, ლინზაში გავლის შემდეგ ასევე ერთ F' წერტილში იყრის თავს, რომელიც გვერდითი ოპტიკური ღერძისა და ფოკალური Ф სიბრტყის გადაკვეთაზე მდებარეობს, ანუ მთავარ ოპტიკურ ფოკუსზე გამავალ მთავარი ოპტიკური ღერძის მართობულ სიბრტყეზე (ნახ. 2). ლინზის ოპტიკურ O ცენტრსა და მთავარ F ფოკუსს შორის მანძილს ფოკუსურ მანძილს უწოდებენ. ისიც F ასოთი აღინიშნება.
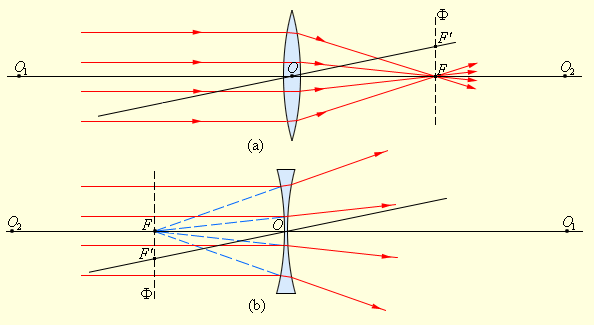
ნახ. 2.
პარალელურ სხივთა კონის გარდატეხა შემკრებ (a) და გამბნევ (b) ლინზებში. O1 და O2 წერტილები სფერული ზედაპირების ცენტრებია, O1O2 – მთავარი ოპტიკური ღერძი, O – ოპტილური ცენტრი, F– მთავარი ფოკუსი, F' – გვერდითი ფოკუსი, OF' – გვერდითი ოპტიკური ღერძი, Ф – ფოკალური სიბრტყე
ლინზის მთავარი თვისება საგნის გამოსახულების მოცემის უნარია.გამოსახულება შიუძლება იყოს პირდაპირი და გადაბრუნებული, ნამდვილი და წარმოსახვითი, გადიდებული და შემცირებული.
გამოსახულების მდებარეობა და მისი ხასიათი შეიძლება გეომეტრიული აგების საშუალებით დადგინდეს. ამისათვის გამოიყენება ზოგიერთი ისეთი სტანდარტული სხივის თვისება, რომელთა სვლაც ცნობილია. ეს სხივები გადიან ოპტუკირ ცენტრზე ან ლინზის ერთ-ერთ ფოკუსზე, და ასევე, პარალელურია მთავარი ოპტიკური ღერძისა ან ერთ-ერთ გვერდითი ოპტიკური ღერძის. ასედი აგების მაგალითები ნახ. 3 -სა და 4-ზეა მოცემული.
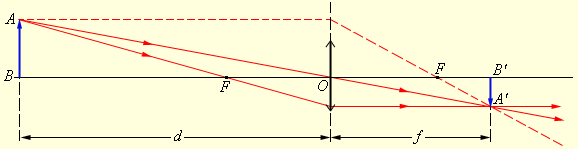
ნახ. 3.
გამოსახულების აგება შემკრებ ლინზაში
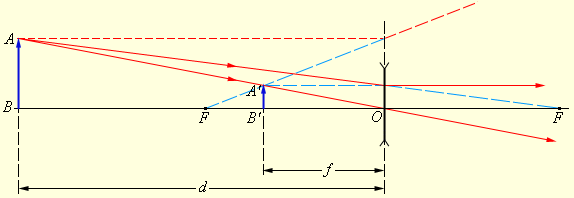
ნახ. 4.
გამოსახულების აგება გამბნევ ლინზაში
ყურადღება უადა მიექცეს იმას, რომ გამოსახულების ასაგებად ნახ.3-სა და 4-ზე გამოყენებული ზოგი სტანდარტული სხივი ლინზაში არ გადის. ეს სხივები გამოსახულების შექმნაში რეალურად არ მონაწილეობენ, მაგრამ აგებისთვის შესაძლებელია მათი გამოყენება.
გამოსახულების მდებარეობა და მისი ხასიათი (ნამდვილია თუ წარმოსახვითი) შეიძლება, აგრეთვე, თხელი ლინზის ფორმულით გაითვალოს. თუ სხეულიდან ლინზამდე მანძილს d -თი ავღნიშნავთ, ხოლო ლინზიდან გამოსახულებამდე f -ით, მაშინ თხელი ლინზის ფორმულა შეიძლება ასე ჩავწეროთ:

D სიდიდე ფოკუსური მანძილის შებრუნებულია და ლინზის ოპტიკურ ძალას უწოდებენ. ოპტიკური ძალის ერთეულია დიოპტრი. დიოპტრი ერთი მეტრი ფოკუსური მანძილის მქონე ლინზის ოპტიკური ძალაა:
1 დიოპტრი = მ–1
თხელი ლინზის ფორმულა სფერული ლინზის ფორმულის ანალოგიურია. იგი პარაქსიალური სხივებისთვის შეიძლება მივიღოთ ნახ. .3 ან 4-დან სამკუთხედების მსგავსებით.
ლინზების ფოკუსურ მანძილებს გარკვეულ ნიშანს ანიჭებენ: შემკრები ლინზისათვის F > 0, ხოლო გამბნევისათვის F < 0.
d და f სიდიდეები ასევე გარკვეულ ნიშანთა წესს ემორჩილებიან:
d > 0 და f > 0 – ნამდვილი საგნებისთვის (ე.ი. სინათლის რეალური წყაროებისათვის, და არა სხივების გაგრძელებებისათვის რომლებიც ლინზის მეორე მხარეს იკრიბებიან) და გამოსახულებებისთვის;
d < 0 და f < 0 – წარმოსახვითი საგნებისა და გამოსახულებისათვის.
ნახ. 3-ზე გამოსახული შემთხვევისთვის გვაქვს: F > 0 (შემკრები ლინზა), d = 3F > 0 (ნამდვილი საგანი).
თხელი ლინზის ფორმულის მიხედვით: 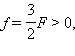 ამიტომ, გამოსახულება ნამდვილია.
ამიტომ, გამოსახულება ნამდვილია.
ნახ. 4-ზე გამოსახული შემთხვევისათვის გავქვს: F < 0 (გამბნევი ლინზა), d = 2|F| > 0 (წარმოსახვითი საგანი), 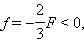 ე.ი. გამოსახულება წარმოსახვითია.
ე.ი. გამოსახულება წარმოსახვითია.
საგნის ლინზის მიმართ მდებარეობაზე დამოკიდებულებით იცვლება გამოსახულების ზომები. ლინზის წრფივი გადიდება ეწოდება გამოსარულებისა h' და საგნის h წრფივი ზომების ფარდობას. h' სიდიდეს, ისევე როგორც სფერული სარკის შემთხვევაში, მოსახერხებელია მივუწეროთ პლიუსი ან მინუსი იმის მიხედვით, გამოსახულება პირდაპირია თუ გადაბრუნებული. h სიდიდე დადებითად ითვლება. ამიტომ პირდაპირი გამოსახულებებისთვის Γ > 0, გადაბრუნებულებისათვის Γ < 0. ნახ. 3 და 4-ზე სამკუთხედების მსგავსებიდან ადვილად მიიღება წრფივი გადიდების ფომულა თხელი ლინზისთვის:
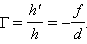
შემკრები ლინზის განხილულ მაგალითში (ნახ. 3.3.3): d = 3F > 0, 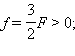 აქედან გამომდინარე,
აქედან გამომდინარე, 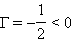 – გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული.
– გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული.
გამბნევი ლინზის შემთხვევაში (ნახ. 4): d = 2|F| > 0,  ; აქედან გამომდინარე,
; აქედან გამომდინარე, 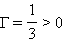 – გამოსახულება პირდაპირია და სამჯერ შემცირებული.
– გამოსახულება პირდაპირია და სამჯერ შემცირებული.
ლინზის ოპტიკური ძალა D დამოკიდებილია მისი სფერული ზედაპირების სიმრუდის R1 და R2 რადიუსებზე და იმ მასალის გარდატეხის მაჩვენებელზე, რომლისგანაცაა ლინზა დამზადებული.
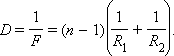
ამოზნექილი ზედაპირის სიმრუდის რადიუსი დადებითად ითვლება, ხოლო ჩაზნელილისა კი - უარყოფითად. ეს ფორმულა გარკვეული ოპტიკური ძალის ლინზის დასამზადებლად გამოიყენება.
მრავალ ოპტიკურ ხელსაწყოში სინათლე მიმდევრობით ორ ან რამდენიმე ლინზაში გადის. პირველი ლინზით მიღებული გამოსახულება მეორე ლინზისთვის საგანს (ნამდვილს ან წარმოსახვითს) წარმოადგენს, რომელიც მეორე ლინზის გამოსახულებას იძლევა. ეს მეორე გამოსახულებაც შეიძლება იყოს ნამდვილი ან წარმოსახვითი. ორ ლინზიანი სისტემის გათვლა დაიყვანება ლინზის ფორმულის ორმაგ გამოყენებაზე, ამასთან პირველი გამოსახულებიდან მეორემდე მანძილი d2 იყოს სიდიდის l – f1 ტოლი, სადაც l – ლინზებს შორის მანძილია. ლინზის ფორმულით გათვლისას f2 სიდიდე განსაზღვრავს მეორე გამოსახულების მდებარეობას და ხასიათს (f2 > 0 – ნამდვილი გამოსახულება, f2 < 0 – წარმოსახვითი). ორი ლინზისგან შემდგარი სისტემის სრული წრფივი გადიდება ორივე ლინზის წრფივ გადიდებათა ნამრავლის ტოლია: Γ = Γ1 · Γ2. თუ საგანი ან მისის გამოსახულება უსასრულობაში მდებარეობს, მაშინ წრფივი გადიდება აზრს კარგავს.
კერძო შემთხვევას ორი ლინზისგან შემდგარ ტელეკოპში სხივთა სვლა წარმოადგენს, როდესაც საგანიც და მეორე გამოსახულებაც უსასრულოდ დიდ მანძილზე მდებარეობენ. სხივთა ტელესკოპური სვლა რეალიზდება მაყურებლის მილებში – კოლერის ასტრონომიულ მილში და გალილეის დედამიწის მილში .
თხელ ლინზებს აქვთ გარკვეული ნაკლოვანებები, რომლებიც არ იძლევიან მაღალხარისხოვანი გამოსახულების მიღების საშუალებას. დამახინჯებებს, რომლებიც გამოსახულების ფორმირებისას მიიღება, აბერაციებს უწოდებენ. მათ შორის უნმიშვნელოვანესია სფერული და ქრომატული აბერაციები. სფერული აბერაცია ვლინდება იმაში, რომ სინათლის ფართო კონაში, ოპტიკური ღერძიდან დიდიდ დაშორებილი სხივები ფოკუსში არ იკვეთებიან. თხელი ლინზის ფორმულა სამართლიანია მხოლოდ ოპტიკური ღერძის მახლობელი სხივებისათვის. შორს მყოფი წერტილოვანი წყარის გამოსახულება, რომელის სხივთა ფართო კონით იქმნება, ლინზაში გავლის შემდეგ გადღაბნილი აღმოჩნდება.
ქრომატული აბერაცია იმითაა გამოწვეულია, რომ ლინზის მასალის გარდატეხის კოეფიციენტი სინათლის ტალღის λ სიგრძეზეა დამოლიდებული. გამჭვირვალე გარემოს ამ თვისებას დისპერსიას უწოდებენ. ლინზის ფოკუსური მანძილი სხვადასხვა ტალღის სიგრძის სინათლისათვის სხვადასხვაა, რასაც არამონოქრომატული ლინძების გამოყენების შმთხვევაში გამოსახულების გადღაბნასთან მივყავართ.
თანამედროვე ოპტიკურ ხელსაწყოებში თხელი ლინზების ნაცვლად, რთული მრავალლინზიანი სისტემები გამოიყენება, რომელებშიც სხვადასხვა აბერაციების გარკვეული მიახლოებით გასწორება ხდება შესაძლებელი.
შემკრები ლინზის საშუალებით ფორმირებული საგნის ნამდვილი გამონასახი მრავალ ოპტიკურ ხელსაწყოში გამოიყენება. მაგ., ფოტოაპარატში, პროექტორში და სხვა.
ფოტოაპარატი დახურული, სინათლეგაუმტარი კამერაა. გადასაღები საგნების გამოსახულება ფოტოფირზე (მიმღებზე) მიიღება ლინზების სისტემით, რომელსაც ობიექტივს უწოდებენ. სპეციალური ჩამკეტი საშუალებას იძლვა ობიექტივი გაიხსნას ექსპოზიციის შესაბამისი ხანგრძლივობით.
ფოტოაპარატის მუშაობის თავისებურება იმაში მდგომარეობს, რომ ბრტყელ მიმღებზე სხვადსხვა მანძილზე მდებარე საგნების საკმაოდ მკვეთრი (მკაფიო) გამოსახულება უნდაი ქნეს მიღებული.
მიმღების სიბრტყეში მკვეთრად მხოლოდ გარკვეულ მანძილზე მდებარე საგნების გამოსახულებები მიიღება. სიმკვეთრე ობიექტივის მიმღების სიბრტყის მიმართ გადაადგილებით მიიღწევა. იმ წერტილების გამოსახულებები, რომლებიც სიმკვეთრის სიბრტყეში არ მდებარეობენ, გაფანტული წრეების სახით იდღაბნება. ამ წრეების d დიამეტრის შემცირება შეიძლება დიაფრაგმირების საშუალებით, ე.ი. ფარდობითი ხვრელის a / F შემცირებით მიიღწეს (ნახ. 5). ამას სიმკვეთრის სიღრმის გადიდებასთან მივყავართ.

ნახ. 5.
ფოტოაპარატი
საპროექციო აპარატი მსხვილმაშტაბოვანი გამოსახულების მისაღებადაა განკუთვნილი. პროექტორის O ობიექტივი ბრტყელი საგნის (დიაპოზიტივიD) გამისახულებას დაშორებულ Э ეკრანზე აფოკუსებს (ნახ. 3.3.6). კონდენსორად წოდებულ ლინზათა K სისტემა S სინათლის წყაროს დიაპოზიტივზე კონცენტრირებისთვისაა განკუთვნილი. Э ეკრანზე ნამდვილი, გადიდებული, გადაბრუნებული გამისახულება მიიღება. საპროექციო აპარატის გადიდება შეიძლება შეიცვალის Э ეკრანის მიახლოებასა ან დაშორებასთან ერთად D დიაპოზიტივსა და O ობიექტივს შორის მანძილის ცვლით.

ნახ. 6.
საპროექციო აპარატი
{loadnavigation}
უმარტივეს მოწყობილობას, რომელსაც საგნის გამოსახულების შემქმნა შეუძლია, ბრტყელი სარკე ეწოდება. ბრტყელი სარკოთ შქმნილი საგნის გამოსახულება სარკის ზედაპირიდან არეკვლილი სხივების საშუალებით იქმნება. ეს გამოსახულება წარმოსახვითია, რადგან ის იქმნება არა თვითონ არეკვლილი სხივების, არამედ მათი გაგრძელებების სარკის მიღმა გადაკვეთით (ნახ. 1).

ნახ. 1.
სარკიდან არეკვლილი სხივების სვლა. S' წერტილი S წერტილის წარმოსახვითი გამოსახულებაა.
სინათლის არეკვლის კანონის შედეგად საგნის წარმოსახვითი გამოსახულება სარკის ზედაპირის მიმართ სიმეტრიულად თავსდება. გამოსახულების ზომა საგნის ზომის ტოლია.
სფერულ სარკეს უწოდებენ ამრეკვლ ზედაპირს, რომელსაც სფერული სეგმენტის სახე აქვს. იმ სფეროს ცენტრს, რომლისაგანაცაა ეს სეგმენტი მოჭრილი სარკის ოპტიკურ ცენტრს უწოდებენ. სფერული სეგმენტის წვეროს პოლუსს უწოდებენ. ოპტიკურ ცენტრსა და პოლუსზე გამავალ სწორს სფერული სარკის მთავარ ოპტიკურ ღერძს უწოდებენ. მთავარი ოპტიკური ღერძი მხოლოდ იმით განსხვავდება ოპტიკურ ცენტრზე გამავალი ყველა სხვა ღერძისაგან, რომ ის სარკის სიმეტრიის ღერძს წარმოადგენს.
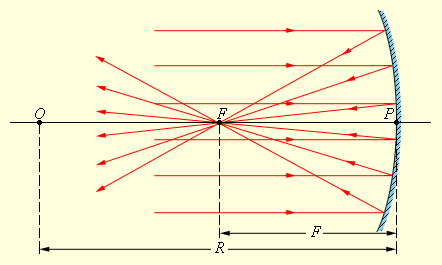
სფერული სარკე შეიძლება იყოს ჩაზნექილი და ამოზნექილი. თუ ჩაზნექილ სფერულ სარკეს მთავარი ოპტიკური ღერძის მთავარი ოპტიკური ღერძის პარალელური სხივთა კონა ეცემა, მაშინ სარკიდან არეკვლის შემდეგ სხივები გადაიკვეთებიან წერტილში, რომელსაც სარკის მთავარი ფოკუსი F ეწოდება. ფოკუსიდან სარკის პოლუსამდე მანძილს ფოკუსურ მანძილს უწოდებენ და აღნინავენ F ასოთი. ჩაზნექილი სფერული სარკის მთავარი ფოკუსი ნამდვილია. ის სარკის ცენტრსა და პოლუსს შორის მანძილის შუაში მდებარეობს (ნახ. 2).
ნახ. 2.
ჩაზნექილი სარკის ზედაპირიბად სხივების პარალელური კონის არეკვლა. O წერტილი ოპტიკური ცენტრია, P - პოლუსი, F - სარკის მთავარი ფოკუსი; OP - მთავარი ოპტიკური ღერძი, R - სარკის სიმრუდის რადიუსი
მხედველობაში უნდა ვიქონიოთ, რომ არეკვლილი სხივები იკვეთება დაახლოებით ერთ წერტილში მხოლოდ იმ შემთხვევაში, თუ დაცემული პარალელური კონა საკმარისად ვიწროა (ე.წ. პარაქსიალური კონა).
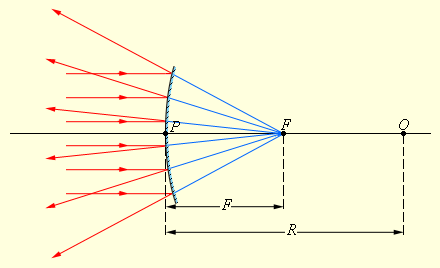
ამოზნექილი სარკის მთავარი ფოკუსი წარმოსახვითია. თუ ამოზნექილი სარკეზე მთავარი ოპტიკური ღერძის პარალელური სხივთა კონა ეცემა, მაშინ არეკვლის შემდეგ ფოკუსში გადაიკვეთება არა თვით სხივები, არამედ მათი გაგრძელებები (ნახ. 3).
ნახ. 3.
ამოზნექილი სარკის ზედაპირიდან სხივების პარალელური კონის არეკვლა. O ოპტიკური ცენტრია, P - პოლუსი, F - სარკის წარმოსახვითი ფოკუსი, OP - მთავარი ოპტიკური ღერძი
სფერული სარკის ფოკუსური მანძილი გარკვეული ნიშანი აქვს: ჩაძნექილი სარკისათვის 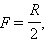 ამოზნექილისათვის
ამოზნექილისათვის 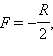 სადაც R – სარკის სიმრუდის რადიუსია.
სადაც R – სარკის სიმრუდის რადიუსია.
სფერულ სარკეში რაიმე A წერტილი გამოსახულება შეიძლება სტანდარტული სხივების ნებისმიერი წყვილის საშუალებით:
- სარკის ოპტუკურ ცენტრზე გამავალი AOC სხივი; არეკვლილი COA სხივი მიჰყვება იგივე სწორს;
- სარკის ფოკუსში გამავალი AFD სხივი; არეკვლილი სხივი მთავარი ოპტიკური ღერძის პარალელურად გადის;
- სარკის პოლუსზე დაცემული AP სხივი; არეკვლილი სხივი დაცემულის სიმეტრიულია მთავარი ოპტიკური ღერძის მიმართ.
- მთავარი ოპტიკური ღერძის პარალელური AE სხივი; არეკვლილი EFA1 სხივი სარკის ფოკუსზე გადის.
ნახ. 4-ზე ზემოთ ჩამოთვლილი სტანდარტული სხივები ჩაზნექილი სარკის მაგალითზეა ნაჩვენები. ყველა სხივი გადის A' წერტილზე, რომელიც A წერტილის გამოსახულებას წარმოადგენს. ყველა სხვა არეკვლილი სხივები ასევე A' წერტილში გადის. სხივთა სვლას, რომლის დროსაც ერთი წერტილიდან გამოსული ყველა სხივი მეორე წერტილში იკრიბება, სტიგმატურს უწოდებენ. A'B' მონაკვეთი AB სხეულის გამოსახულებაა. აგება ამოზნექილი სარკისათვისაც ანალოგიურია.

ნახ. 4.
გამოსახულების აგება ჩაზნექილ სფერულ სარკეში
გამოსახულების მდებარეობა და ზომა შეიძლება განისაზღვროს სფერული სარკის ფორმულისათვის:

სადაც d – სხეულიდან სარკემდე მანძილი, f – სარკიდან გამოსახულებამდე მანძილი. d და f სიდიდეები ნიშნების გარკვეულ წესს ემორჩილება:
- d > 0 და f > 0 – ნამდვილი საგნებისა და გამოსახულებებისთვის;
- d < 0 და f < 0 – წერმოსახვითი საგნებისა და გამოსახულებებისთვის.
ნახ. 4-ზე გამოსახული შემთხვევისათვის გავაქვს:
F > 0 (ჩაზნექილი სარკე); d = 3F > 0 (ნამდვილი საგანი).
სფერული სარკის ფორმულით ვღებულობთ: 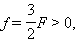 , აქედან გამომდინარე, გამოსახულება ნამდვილია.
, აქედან გამომდინარე, გამოსახულება ნამდვილია.
ჩაზნექილი სარკის ადგილას, სიდიდით ისეთივე ფოკუსური მანძილის მქონე, ამოზნექილი სარკე რომ იყოს ჩვენ მივიღებთ შემდეგ შედეგს:
F < 0, d = –3F > 0, 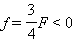 – წარმოსახვითი გამოსახულება.
– წარმოსახვითი გამოსახულება.
სფერული სარკის წრფივი გადიდება Γ განისაზღვრება როგორც გამოსახულების h' და საგანის h სიდიდეების ფარდობისა.
h' სიდიდეს მოსახერხებელია მივუწეროთ გარკვეული ნიშანი იმის მიხედვით, გამოსახულება პირდაპირია (h' > 0) თუ გადაბრუნებული (h' < 0). h სიდიდე ყოველთვის დადებით სიდიდეთ ითვლება. ასეთი განსაზრვრის დროს სფერული სარკის წრფივი გადიდება გამოისახება ფორმულით; რომელიც ნახ. 4-დან ადვილად მიიღება:
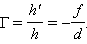
ზემოთ განხილულ პირველ მაგალითში  – გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული. მეორე მაგალითში
– გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული. მეორე მაგალითში  – გამოსახულება პირდაპირია და ოთხჯერ შემცირებული.
– გამოსახულება პირდაპირია და ოთხჯერ შემცირებული.
