{loadnavigation}

თვითინდუქცია ელექტრომაგნიტური ინდუქციის იმ მნიშვნელოვან კერძო შემთხვევას წარმოადგენს, როცა ინდუქციის ემძ-ს გამომწვევი ცვლადი მაგნიტური ნაკადი თვით, გამტარში გამავალი დენით აღიძვრება. თუ განსახილვევ კონტურში დენი რაიმე მიზეზით იცვლება, იცვლება ამ დენის მაგნიტური ველიც, და შედეგად იცვლება თვით, ამ კონტურის განმჭოლი,  მაგნიტური ნაკადი. კონტურში თვითინდუქციის ემძ აღიძვრება, რომელიც ლენცის წესის თანახმად ხელს უშლის კონტურში დენის ცვლილებას.

დენიანი კონტურის ან კოჭას განმჭოლი, საკუთარი მაგნიტური ნაკადი Φ დენის I ძალის პროპორციულია:

Φ = LI.

ამ ფორმულაში პროპორციულობის კოეფიციენტს კოჭას თვითინდუქციის კოეფიციენტს ან ინდუქტიურობას უწოდებენ. სი სისტემაში ინდუქტიურობის ერთეულს ჰენრი (ჰ) ეწოდება. კონტურის ან კოჭას ინდუქციურობა 1 ჰენრის ტოლია, თუ 1 ა  დენის ძალისაა საკუთარი ნაკადი 1 ვბ-ს ტოლია:

 1 ჰ = 1 ვბ / 1 ა

მაგალითისათვის გავითვალოთ N  ხვიის, S განივკვეთისა და l სირძის მქონე გრძელი სოლენოიდის ინდუქტიურიბა. სოლენოიდის მაგნიტური ველი განისაზღვრება ფორმულით

B = μ₀ I n,

სადაც I – დენია სოლენოიდში, n = N / \(l\) –  ხვიათა რიცხვი სოლენოიდის ერთეულ სიგრძეზე.

მაგნიტური ნაკადი, რომელიც სოლენოიდის ყველა ხვიას განჭოლავს, ტოლია

Φ = B S N = μ₀ n² S l I.

აქედან გამომდინარე, სოლენოიდის ინდუქტიურობა ტოლია  

L = μ₀ n² S l = μ₀ n² V,

სადაც V = Sl – სოლენოიდის ის მცულობაა, რომელშიც მაგნიტური ველია თავმოყრილი. მიღებული შედეგი კიდის ეფექტებს არ ითვალისწინებს, ამიტომ ის მიახლოებით  მხოლოდ საკმარისად გრძელი კოჭასათვისაა სამართლიანი. თუ სოლენოიდი ამოვსებულია μ მაგნიტური შეღწევადობის ნივთიერებით, მაშინ განსაზღვრული ინდუქციის დენის შემთხვევაში მაგნიტური ველი სიდიდით  μ -ჯერ იზრდება; ამიტომ გულიანი კოჭას ინდუქციურობაც იზრდენა μ -ჯერ:

L_μ = μ L = μ₀ μ n² V.

თვითინდუქციის ემძ, რომელიც აღიძვრება მუდმივი ინდუქტიურონის მნიშვნელობის მქონე კოჭაში, ფარადეის კანონის თანახმად ტოლია

_ინდ\(=\)_L\(=-\frac{\Delta \Phi }{\Delta t}=-L\frac{\Delta I}{\Delta t}\)

თვითინდუქციის ემძ კოჭას ინდიქტიურობის და დენის ცვლილების სიჩქარის პროპორციულია.

მაგნიტურ ველს აქვს ენერგია. ამის მსგავსად, ისევე როგორც დამუხტულ კონდენსატორს აქვს ელექტრული ენერგიის მარაგი, კოჭაშიც, რომლის ხვიებშიც დენი გადის, არის მაგნიტური ენერგიის მარაგი. თუ მუდმივი დენის ელექტრულ წრედში დიდ ინდუქტიურიბის მქონე კოჭას პარალელურად ელექტრულ ნათურას ჩავრთავთ, მაშინ ჩამრთველის ჩართვისას ნათურის ხანმოკლე ანთება (გაბრწყინება) დაიკვირვება (ნახ. 1). წრედში დენი აღიძვრება ინდუქციის ემძ-ს მოქმედებით. ამ დროს წრედში გამოყოფილი ენერგიის წყაროს კოჭას მაგნიტური ველი წარმოადგენს.

 

ნახ. 1.

კოჭას მაგნიტური ენერგია. ჩამრთველის ჩართვისას მოხდება ნათურის ხანმოლკე ანთება (გაბრწყინება)

ენერგიის შენახვის კანონიდან გამომდინარე, კოჭაში მომარაგებული მთელი ენერგია ჯოულის სითბის სახით გამოიყოფა. თუ R-ით ავღნიშნავთ წრედის სრულ წინაღობას, მაშინ Δt დროის განმავლობაში გამოყოფილი სითბოს რაოდენობა ტოლია ΔQ = I² R Δt.

 წრედში დენი ტოლია

გამისახულება ΔQ -სთვის ასე შეიძლება ჩაიწეროს 

ΔQ = –L I ΔI = –Φ (I) ΔI.

ამ გამოსახულებაში ΔI < 0; წრედში დენი თანდათან მცირდება საწყისი I₀ მნიშვნელობიდან ნულამდე. წრედში გამოყოფილი სრული სითბოს რაოდენობის მიღება შესაძლებელია I₀-დან 0-მდე ინტეგრირებით. მივიღებთ

ამ ფორმულის მოღება შეიძლება გარაფიკული მეთოდით, გრაფიკზე მაგნიტური ნაკადის Φ (I)-ს დენის I  ძალაზე დამოკიდებულების გამოსახვით (ნახ. 2). გამოყოფილი სითბის სრული მნიშვნელობა, რომელიც მაგნიტური ველის საწყისი მარაგის ტოლია,  ნახ.1-ზე გამოსახული სამკუთხედის ფართობით განისაზღვრება.

  

ნახ. 2.

მაგნიტური ველის ენერგიის გამოთვლა

ამგვარად, L ინდუქციურობის მქონე კოჭას მაგნიტური ველის ენერგია W_м , რომელიც I დენით აღიძვრება, ტოლია

მიღებული გამოსახულება გამოვიყენოთ მაგნიტური გულიანი გრძელი კოჭას მაგნიტური ველის ენერგიის მისაღებად. ზემოთ მოყვანილი სოლენოიდის თვითინდუქციის L_μ  კოეფიციენტისა და I დენით აღძრული B მაგნიტური ველის ფორმულების გამოყენებით შეიძლება მივიღოთ:

სადაც V – სოლენოიდის მოცულობაა. ეს გამოსახულება უჩვენებს, რომ მაგნიტური ენერგია კოჭას ხვიებში კი არ არის თავმოყრილი, რომლებშიც დენი გადის, არამედ მთელ მოცულობაშია განაწილებული სადაც მაგნიტური ველი წარმოიქმნება. ფიზიკური სიდიდეს

რომელიც მოცულობის ერთეულში მაგნიტური ველის ენერგიის ტოლია, მაგნიტური ენერგიის მოცულობითი სიმკვრივეს უწოდებენ.  მაქსველმა უჩვენა, რომ გრძელი სილენოიდისთვის გამოყვანილი მაგნიტური ენერგიის მოცულობითი სიმკვრივის ეს გამოსახულიბა ნებისმიერი მაგნიტური ველისათვისაა სამართლიანი.

{loadnavigation}

ელექტრომაგნიტური ინდიქციის მოვლენა დიდ ინგლისელი ფიზიკოსის მ.ფარადეის მიერ იქნა აღმოჩენილი 1831 წელს. იგი იმაში მდგომარეობს, რომ ჩაკეტილი გამტარის კონტურის განმჭოლი მაგნიტური ნაკადის დროში ცვლილების შედეგად ამ კონტურში ელექტრული ველი აღიძვრება.

S კონტურის განმჭოლი მაგნიტური Φ ნაკადი ეწოდება სიდიდეს

Φ = B · S · cos α,

სადაც B – მაგნიტური ინდუქციის ვექტორის სიდიდეა, α – 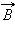 ვექტორსა და კონტურის სიბრტყის  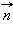მართობს შორის კუთხეა (ნახ. 1).

  

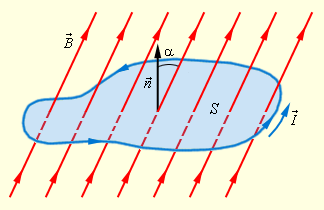
ნახ. 1.

ჩაკეტილი კონტურის გამსჭვალავი მაგნიტური ნაკადი. 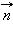 მართობისა დაკონტურის შემოვლის  არჩეული დადებითი მიმართულება დაკავშირებულია მარჯვენა ბურღის წესთან

მაგნიტური ნაკადის განმარტება იოლად შეიძლება განზოგადდეს არაერთგვაროვანი მაგნიტური ველისა ან კონტურისათვის, რომელიც ბრტყელი არ არის. სი სისტემაში მაგნიტური ნაკადის ერთეულს ვებერი ეწოდება (ვბ). 1 ვბ-ს ტოლი მაგნიტური ნაკადი იქმნება 1 ტესლა ინდუქციის მაგნიტური ველით, რომელიც 1  მ²   ფართობის ბრტყელი კონტურს განჭოლავს:

1 ვბ = 1 ტს · 1 მ².

ფარადეიმ ექსპერიმენტულად დაადგინა, რომ მაგნიტური ნაკადის ცვლილებისას გამტარ კონტურში აღიძვრება ინდუქციის ემძ _ინდ, რომელიც კონტურით შემოსაზღვრულ ზედაპირის განმჭოლავი მაგნიტური ნაკადის ცვლილების სიჩქარის ტოლია მინუს ნიშნით:

ეს ფორმულა ფარადეის კანონის სახელითაა ცნობილი. 

ცდები უჩვენებენ, რომ ჩაკეტილ კონტურში მისი განმჭოლი მაგნიტური ნაკადის ცვლილებისას აღძრული ინდუქციური დენი, ყოველთვის ისეა მიმართული, რომ მის მიერ შექმნილი მაგნიტური ველი ხელს უშლის ინდუქციური დენის გამომწვევი მაგნიტური ნაკადის ცვლილებას. ეს მტკიცებულობა, ფორმულირებული 1833 წელს, ლენცისწესის სახელითაა ცნიბილი.

ნახ. 2-ზე ერთგვაროვან მაგნიტურ ველში, რომლის ინდუქციის სიდიდე იზრდება დროში, მოთავსებული უძრავი გამტარის კონტურის მაგალითზე  ლენცის წესია ილუსტრურებული.

 

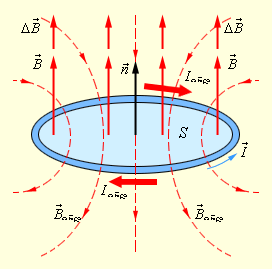
ნახ. 2.

ლენცის წესის ილუსტრაცია. ამ მაგალითში   ხოლო _ინდ < 0. ინდუქციური დენი I_ინდ    მიემართება კონტურის შემოვლის   მიმართულების შესახვედრად

ლენცის წესი იმ ექსპერიმენტულ ფაქტს ასახავს, რომ _ინდ  და 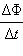ყოველთვის ურთიერთსაწინააღმდეგო ნიშნები აქვთ (ნიშანი „მინუსი“ ფარადეის ფორმულა). ლენცის წესს ღრმა ფიზიკური არსი აქვს - ის გამოსახავს ენერგიის შენახვის კანონს.

ჩაკეტილი კონტურის განმჭოლი მაგნიტული ნაკადის ცვლილება შეიძლება ორი მიზეზით ხდებოდეს.

1. მაგნიტური ნაკადი იცვლება კონტურის ან მისი ნაწილების დროში მუდმივ მაგნიტურ ველში გადაადგილების შედეგად. ეს შემთხვევაა, როცა გამტარი და მასთან ერთად მუხტის თავისუფალი მატარებლები მაგნიტურ ველში მოძრაობენ. ინდუქციის ემძ   გამტარში მოძრავ თავისუფალ მუხტებზე ლორენცის ძალის მოქმედებით  აღიძვრება. ლორენცის ძალა ამ შემთხვევაში იგივე როლს თამაშობს რასაც გვერდითი ძალები.

მაგალითის სახით განვიხილოთ თუ როგორ აღიძვრება ინდუქციის ემძ მართკუთხა კონტურში, რომელიც   კონტურის სიბრტყის მართობულ ერთგვაროვან მაგნიტურ  ველშია მოთავსებული. ვთქვათ კონტურის l  სიგრძის  ერთ-ერთი გვერდი  სხვა ორ გვედზე სრიალებს  სიჩქარით (ნახ. 3).

 

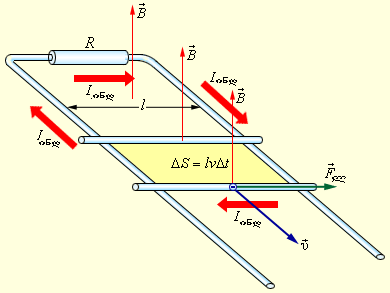
 ნახ. 3.

ინდუქციის ემძ-ის აღძვრა მოძრავ გამტარში. თავისუფალ ელექტრონზე მომქმედი ლორენცის ძალის მდგენელია მითითებული

 

თავისუფალ მუხტებზე კონტურის ამ უბანზე მოქმედებს ლორენცის ძალა. ამ ძალის ერთ-ერთი მდგენელი, რომელიც მუხტის გადატანით   სიჩქარესთანაა დაკავშირებული, მიმართულია გამტარის გასწვრივ. ეს მდგენელი ნახ. 3-ზეა მითითებული. მისი სიდიდე ტოლია

F_ლ = eυB

l  გზაზე F_ლ ძალის მუშაობა ტოლია

A = F_ლ · l = eυBl.

განმარტების მიხედვით ემძ

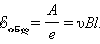
კონტურის სხვა, უძრავ გვერდებში გვერდითი ძალა ნულის ტოლია. გამოსახულებას _ინდ -სათვის შეიძლებას მიეცეს ჩვეული სახე. Δt დროის განმავლობაში კონტურის ფართობი იცვლება ΔS = lυΔt-ით. ამავე დროში მაგნიტური ნაკადის ცვლილება ტოლია ΔΦ = BlυΔt. აქედან გამომდინარე,

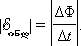
_ინდ-სა და 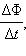 დამაკავშირებელ ფორმულაში ნიშნის დასადგენად, უნდა აირჩეს მარჯვენა ბურღის წესით  ერთმანეთთან შეთანხმებული,  მართობის  მიმართულება და კონტურის შემოვლის დადებითი მიმართულება , ისე როგორც ნახ. 1 და 2-ზეა მოცემული. ასე ადვილად მივალთ ფარადეის ფორმულასთან.

თუ მთელი წრედის წინაღობა R-ის ტოლია, მაშინ მასში გამავალი ინდუქციური დენი ტოლია

I_ინდ = _ინდ/R.

Δt დროში R წინაღობაზე გამოყოფილი ჯოულის სითბო ტოლია

ისმის კითხვა: ლორენცის ძალა მუშაობას არ ასრულებს და მაშინ საიდან მოდის ეს ენერგია! ეს პარადოქსი იმიტომ წარმოიქმნება, რომ ჩვენ გავითვალისწინეთ ლორენცის ძალის მხოლოდ ერთი მდგენელი.  მაგნიტურ ველში მოთავსებულ გამტარში ინდუქციური დენის გავლისას თავისუფალ მუხტებზე მოქმედებს ლორენცის ძალა, რომელიც გამტარის გასწვრის მუხტების მიძრაობის ფარდობით სიჩქარესთანაა დაკავშირებული. ეს მდგენელი  ამპერის 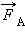  ძალის გამოვლინებაზეა პასუხისმგებელი. ნახ. 3-ზე გამოსახული შემთხვევისათვის ამპერის ძალის სიდიდე ტოლია F_A= I B l. ამპერის ძალა მიმართულია გამტარის მოძრაობის შემხვედრი მიმართულებით; ამიტომ ის ასრულებს უარყოფისთ მექანიკურ მუშაობას. Δt დროში A_მექ  მუშაობა ტოლია

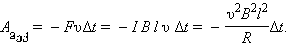
მაგნიტურ ველში მოძრავი გამტარი, რომელშიც ინდუქციური დენი გადის,  მაგნიტურ დამუხრუჭებას განიცდის.  ლორენცის ძალის სრული მუშაობა ნულის ტოლია. კონტურში ჯოულის სითბო გამოიყოფა ან გარე ძალის მუშაობით, რომელიც უზრუნვეყოფს გამტარის სიჩქარის მუდმივობას, ან გამტარის კინეტიკური ენერგიის შემცირების ხარჯზე.

2. კონტურის განმჭოლი მაგნიტური ნაკადის ცვლილების მეორე მიზეზია უძრავი კონტურის შემთხვევაში მაგნიტური ველის ცვლილება დროში. ამ დროს  ინდუქციის ემძ აღძვრა უკვე არ შეიძლება აიხსნას ლორენცის ძალის მოქმედებით. უძრავ გამტარში ელექტრონების მიძრაობაში მოყვანა მხოლოს ელექტრულ ველს შეუძლია. ეს ელექტრული ველი დროში ცვალებადი მაგნიტური ველის საშუალებით იშვება. ჩაკეტილ კონტურში ერთეულოვანი დადებითი მუხტის გადაადგილებისას ამ ველის მუშაობა  უძრავ გამტარში ინდუქციის ემძ-ს ტოლია. აქედან გამომდინარე, მაგნიტური ველის ცვლილებით მიღებული ელექტრული ველი არ არის პოტენციური. მას გრიგალურ ელექტრულ ველს უწოდებენ. წარმოდგენა გრიგალურ ელექტრულ ველზე ფიზიკაში ინგლისელმა ფიზიკოსმა ჯ.მაქსველმა ჯ.მაქსველმა შემოიტანა 1861 წელს.

უძრავ გამტარში ელექტრომაგნიტური ინდუქციის მოვლენაც, რომელიc გარემომცველი მაგნიტური ველის ცვლილებისას აღიძვრება ისევ ფარადეის ფორმულით აღიწერება. ამგვარად, ინდუქციის მოვლენა მოძრავ და უძრავ გამტარებში ერთნაერად მიმდინარეობს, მაგრამ ინდუქციური დენის გამომწვევი ამ ორი შემთხევებისათვის სხვადსხვაა: მოძრავი გამტარის შემთხვევაში ინდუქციის ემძ ლორენცის ძალითაა განპირობებული; უძრავი გამტარისათვის ინდუქციის ემძ-ს მიზეზი თავისუფალ ელექტრონებზე, მაგნიტური ველის ცვლილებით აღძრული, გრიგალირი ელექტრული ველის მოქმედების შედეგია.

{loadnavigation}

ექსპერიმენტულმა კვლევებმა უჩვენეს, ნივთიერებებს მეტნაკლებად აქვთ მაგნიტური ველი. თუ ორი დენიან ხვიას რაიმე გარემოში მოვათავსებთ, მაშინ დენებს შორის ურთიერთქმედების მაგნიტური ძალა იცვლება. ეს ცდა უჩვენებს, რომ ნივთიერების ელექტრული ველებით შექმნილი მაგნიტური ველის ინდუქცია განსხვავდება იგივე დენების მიერ ვაკუუმში შექმნილი მაგნიტური ველის ინდუქციისაგან.

ფიზიკური სიდიდე, რომელიც უჩვენებს თუ სიდიდით რამდენჯერ განსხვავდება  ერთგვაროვან გარემოში \(\vec{B}\) მაგნიტური ველის  ინდუქცია ვაკუუმში \(\vec{B}_{0}\) მაგნიტური ველის ინდუქციისაგან, მაგნიტური შეღწევადობა ეწოდება:

 \(\mu =\frac{B}{B_{0}}\).

ნივთიერებების მაგნიტური თვისებები განისაზღვრება იმ ატომებისა და ელემენტარული ნაწილაკების (ელექტრონების, პროტონების და ნეიტრონების) მაგნიტური თვისებებით, რომლებისაგან შედგება ატომი. დღეისათვის დადგენილია, რომ პროტონების  და ნეიტრონების მაგნიტური თვისებები 1000-ჯერ უფრო ნაკლებია ელექტრონების მაგნიტურ თვისებებზე. ამიტომ ნივთიერების მაგნიტური თვისება ძირითადად მის შემადგენლობაში შემავალი ელექტრონებით განისაზღვრება.

ელექტრონის ერთერთ მნიშვნელოვან თვისებას წარმოადგენს, მის გარშემო არა მარტო ელექტრული, არამედ საკუთარი მაგნიტური ველის არსებობა. ელექტრონის საკუთარ მაგნიტურ ველს სპინურს (spin – ბრუნვა) უწოდებენ. ელექტრონი მაგნიტურ ველს ქმნის ატომგულის გარშემო ორბიტაზე ბრუნვის დროსაც. ეს ბრუნვა შეგვიძლია შევადაროთ წრიულ მიკროდენს. სწორედ  ელექტრონების სპინური ველი და ორბიტალური მოძრაობით გამოწვეული მაგნიტური ველი განსაზღვრავს ნივთიერების მაგნიტური თვისებების ფართო სპექტრს.

ნივთიერებები მაგნიტური თვისებების მიხედვით უკიდურესად განსხვავდებებიან. ნივთიერებების უმრავლესიბაში ეს თვისებები სუსტადაა გამოსახული. სუსტად-მაგნიტული ნივთიერებები იყოფიან ორ დიდ ჯგუფად - პარამაგნიტები და დიამაგნიტები. ისინი იმით განსახვავდებიან, რომ გარე ველში შეტანისას პარამაგნიტური ნივთიერებები ისე დამაგნიტდებიან, რომ მათი საკუთარი მაგნიტური ველი გარე ველის მიმარტულების აღმოჩნდება მიმართული, ხოლო დიამაგნიტები კი მაგნიტდებიან გარე ველის საწინააღმდეგოდ. ამიტომ პარამაგნიტებსათვის μ > 1, ხოლო დიამგნიტებისათვის μ < 1. μ-ს ერთისაგან განსხვავება პარა- და დიემაგნიტებისათვის ძალიან მცირეა. მაგალითად, ალუმინისათვის, რომელიც პარამაგნიტებს განეკუთვნება, μ – 1 ≈ 2,1·10^–5, რკინის ქლორიდისთვის კი (FeCl₃)μ – 1 ≈ 2,5·10^–3. პარამაგნიტებს განეკუთვნება ასევე პლატინა, ჰაერი და მარვალი სხვა ნივთიერება. დიამაგნიტებს განეკუთვნება სპილენძი (μ – 1 ≈ –3·10^–6), წყალი (μ – 1 ≈ –9·10^–6), ბისმუტი (μ – 1 ≈ –1,7·10^–3) და სხვა ნივთიერებები. ელექტრომაგნიტის პოლუსებს შორის არაერთგავაროვან მაგნიტურ ველში მოთავსებული პარა- და დიამაგნიტები სხვადასხვანაირად იქცევიან - პარამაგნიტები მიიზიდებიან ძლიერი ველის არისკენ, დიამაგნიტები კი - გამოიდევნებიან (ნახ. 1).

 

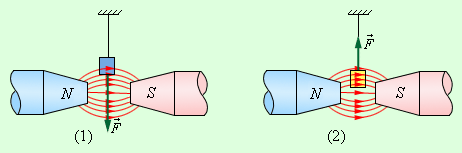
ნახ. 1.

პარამაგნიტები და დიამაგნიტები არაერთგავაროვან მაგნიტურ ველში

პარა- და დიამაგნიტიზმი გარე მაგნიტურ ველში ელექტრონების ორბიტების ქცევით აიხსნება. დიამაგნიტური ნივთიერებების ატომებს გარე ველის არ არსებობის შემთხვევაში ელექტრონების  საკუთარი მაგნიტური ველი და ორბიტული მოძრაიობით შექმნილი ველი მთლიანად  კომპენსირებულია (გაწონასწორებულია). დიამაგნიტიზმის წარმოქმნა ლორენცის ძალის  ელექტრულ ორბიტებზე ზემოქმედებასთანაა დაკავშირებული. ამ ძალის მოქმედებით ელექტრონების ორბიტული მოძრაობის ხასიათი იცვლება და მაგნიტური ველების კომპენსაცია ირღვევა. ამ დროს წარმოქმნილი ატომის საკუთარი ველი გარე ველი ინდუქციის საწინააღმდეგოდ აღმოჩნდება მიმართული.

პარამაგნიტური ნივთიერების ატომებში ელექტრონების მაგნიტური ველი მთლიანათ არ არის კომპენსირებული, და ატომი პატარა წრიულ დენს ემსგავსება. გარე ველის არ არსებობის შემთხვევაში ეს  წლიული მიკროდენები თვითნებურადაა ორიენტირებული, ისე რომ ჯამური მაგნიტური ინდუქცია ნულის ტოლია. გარე მაგნიტური ველი მაორიენტირებემ ზემოქმედებას ახდენს - მიკროდენები ცდილობენ ისე განლაგდნენ, რომ მათი საკუთარი მაგნიტური ველი გარე ველის ინდიქციის მიმართულებას დაემთხვეს. ატომების სითბური მოძრაობის გამო მიკროდენების ორიენტაცია არასოდეს არ არის სრული. გარე ველი გაძლიერების შემთხვევაში მაორიენტირებელი ეფექტი ძლიერდება, ისე რომ პარამაგნიტური ნიმუშის საკუთარი მაგნიტური ველი იზრდება გარე მაგნიტური ველის ინდუქციის პირდაპირპროპორციულად. ნიმუშის მაგნიტური ველის სრული ინდუქცია გარე მაგნიტური ველის ინდუქციისა და დამაგნიტების პრიცესში წარმოქმნილი საკუთარი ველის ინდუქციის შეკრებით მიიღება. პარამაგნიტების დამაგნიტების მექანიზმი ძალიან ჰგავს პოლარული დიელექტრიკების პოლარიზაციის მექანიზმს.  დიამაგნიტიზმს ნივთიერების ელექტრულ თვისებებს შორის ანალოგი არ გააჩნია.

უნდა აღინიშნოს, რომ დიამაგნიტური თვისებები აქვთ ნებისმიერი ნივთიერების ატომებს. მაგრამ ბევრ შემთხვევაში დიამაგნიტიზმი იფარება უფრო ძლიერი პარამაგნიტური ეფექტით. დიამაგნიტიზმის მოვლენა აღმოაჩინა მ.ფარადეიმ 1845 წელს.

ნივთიერებებს, რომლებსაც მაგნიტურ ველში შეუძლეათ ძლიერად დამაგნიტდნენ ფერომაგნიტებს უწოდებენ. მაგნიტების მაგნიტური შეღწევადობა სისდიდის რიგის მიძედვით 10²–10⁵ დიაპაზონში მდებარეობს. მაგალითად, ფოლადისთვის μ ≈ 8000, რკინისა და ნიკელის შენადნობისათვის მაგნიტური შეღწევადიბა აღწევს 250000 მნიშვნელობას.

ამავე ჯგუფს მიეკუთნება ოთხი ქიმიური ელემენტი: რკინა, ნიკელი, კობალტი და გადოლინი. მათ შორის ყველაზე დიდი მაგნიტური შეღწევადობა რკინას აქვს. ამიტომ მთელმა ამ ჯგუფმა მიიღო ფერომაგნიტების სახელწოდება.

ფერამაგნიტებს შეიძლება სხვადსხვა, ფერომაგნიტური ელემენტის შემცველი, შენადნობები წარმოადგენდნენ. ტექნიკაში ფართოდ გამოიყენება კერამიკული ფერომაგნიტური მასალები - ფერიტები.

ყოველი ფერომაგნიტისთვის არსებობს გარკვეული ტემპერატურა (ე.წ კიურის ტემპერატურა ან წერტილი), რომელს ზევითაც ფერომაგნიტური თვისებები ქრებიან და ნივთიერბა პარამაგნიტად გადაიქცევა. რკინისთვის, მაგალითად, კიურის ტემპერატურა ტოლია 770 °C, კობალტისათვის 1130 °C, ნიკელისათვის 360 °C.

ფერომაგნიტური მასალები იყოფიან ორ დიდ ჯგუფად მაგნიტურად-რბილ და მაგნიტურად-ხისტ მასალებად. რბილი ფერომაგნიტური მასალები თითქმის მთლიანად განმაგნიტდებიან, როცა გარე მაგნიტური ველი ნულის ტოლი ხდება. მაგნიტურად-რბილ მასალებს მიეკუთნებიან, მაგალითად, სუფთა რკინა, ელექტროტექნიკური ფოლადი და ზოგიერთი შენადნობი. ეს მასალების ცვალდაი დენის ხელასწყოებში გამოიყენებიან, როლებშიც უწყვეტი გადამაგნიტება მიმდინარეობს, ანუ მაგნიტური ველის მიმართულება იცვლება (ტრანსფორმატორები, ელექტროძრავები და სხვა).

მაგნიტურად-ხისტი მასალები დამაგნიტებულობას მაგნიტური ველიდან გამოტანის მერეც მნიშვნელოვნად ინარშუნებენ. მაგნიტურად-ხისტი მასალების მაგალითებს წარმოადგენენ ნახშირბადიანი ფოლადი და რიგი სპეციალური შენადნობებისა. მაგნიტურად-ხისტ მასალებს ძირითადად მუდმივი მაგნიტების დასამზადებლად გამოიყებებიან.

ფერომაგნიტების მაგნიტური შეღწევადობა μ არ არის მუდმივი სიდიდე; ის B₀ გარე ველის იმდუქციაზე   ძლიერადაა დამოკიდებული. ნახ. 2-ზე ტიპური μ (B₀) დამოკიდებულებაა მოყვანილი. ცხილებში ჩვეულებრივ მაგნიტური შეღწევადობის მაქსიმალური სიდიდეა მოყვანილი.

 

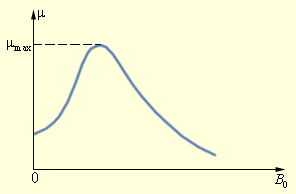
 ნახ. 2.

ფერომაგნიტის მაგნიტური შეღწევადობის ტიპური დამოკიდებულება გარე ველის ინდუქციაზე

მაგნიტური შეღწევადობის არა მუდმივობას რთულ არაწრფივ დამოკიდებულებებთან მივყავართ ფერომაგნიტში B მაგნიტური ველის ინდუქციასა და გარე B₀ მაგნიტური ველის ინდუქციას შორის. ფერომაგნიტის დამაგნიტების პროცესის დამახასიათებელ თავისებურებას ე.წ. ჰისტერეზისის მოვლევა წარმოადგენს, ანუ დამაგნიტების დამოკიდებულება ნიმუშის პრეისტორიასთან. ფერომაგნიტური ნიმუშის დამაგნიტების B (B₀) მრუდი რთული ფორმის მარყუჟს წარმოადგენს, რომელსაც ჰისტერეზისის მარყუჟს უწოდებენ (ნახ. 3).

   

ნახ. 3.

ფერომაგნიტის ჰისტერეზისის მარყუჟი. ისრებით ფერომაგნიტური ნიმუშის დამაგნიტებისა და განმაგნიტების პროცესის მიმართულებაა მითითებული გარე ველის B₀  ინდუქციის ცვლილებისას

ნახ. 3-ზე ჩანს, რომ როცა \(\left | B_{0} \right |> B_{0S}\) მაგნიტური გაჯერება ხდება - ნიმუშის დამაგნიტებულობა მაქსიმუმს აღწევს.

თუ ახლა გარე ველის მაგნიტურ B₀  ინდუქციას შევამცირებთ და ისევ ნულოვან მნიშვნელობამდე დავიყვანთ, ფერომაგნიტი შეინარჩუნებს ნარჩენ დამაგნიტებას - ნიმუშის შიგნით ველი B_r-ს ტოლი იქნება. ნიმუშების ნარჩენი დამაგნიტება მუდმივი მაგნიტების შექმნის საშუალებას იძლევა. ნიმუშის სრული განმაგნიტებისთვის აუცილებელია, გარე ველის ნიშნის შეცვლით, მაგნიტური B₀ ინდუქციის მნიშვნელობის მიყვანა B_0c-მდე, რომელსაც კოერციტიულ ძალას უწოდებენ. შემდეგ გადამაგნიტების პროცესი შეიძლება გაგრძელდეს, ისე როგორც ნახ. 3-ზეა ნაჩვენები.

მაგნიტურად-რბილი მასალებისთვის კოერციტიული ძალა B_0c  დიდი არ არის - ჰისტერეზისის მარყუჟი ასეთი მასალებისთვის საკმაოდ ვიწროა. კოერციტიული ძალის დიდი მნიშვნელობის მასალები, ანუ ჰისტერეზისის ფართო მარყუჟის მქონე მასალები, მაგნიტურად-ხისტ მასალებს განეკუთვნებიან.

ფერომაგნიტიზმის ბუნება ბოლომდე მხოლოდ ქვანტური წარმოდგენების საფუძველზე შეიძლება იქნეს გაგებული. ფერომაგნიტიზმი თვისობრივად ელექტრონების საკუთარი (სპინური) მაგნიტური ველების არსებობით შეიძლება იქნეს ახსნილი.  ფერომაგნიტური მასალების კრისტალებში იქმნება პირობები, როცა მეზობელი ელექტრონების სპინური მაგნიტური ველების ძლიერი ურთიერთქმედების შედეგად, ენერგეტიკულად ხელსაყრელი ხდება მათი პარალელური ორიენტაცია. ასეთი ურთიერთქმედების შედეგად ფერომაფნიტის კრისტალის შიგნით წარმოიქმნება თვითნებურად დამაგნიტებილი არეები 10^–2–10^–4 სმ რიგის ზომებით. ამ არეებს დომენებს უწოდებენ. ყოველი დომენი პატარა მუდმივ მაგნიტს წარმოადგენს.

გარე მაგნიტური ველის არ არსებობის შემთხვევაში დიდი კრისტალის სხვადასხვა დომენში მაგნიტური ველის ინდუქციის ვექტორები ქაოტურადაა ორიენტირებულია. ასეთი კრისტალები საშუალოდ დამაგნიტებული არ არის. გარე მაგნიტურ B₀  ველში მოხვედრისას ხდება დომენების საზღვრების გადანაცვლება, ისე რომ გარე ველის გასწვრივ ორიენტირებული დომენების  მოცულობა იზრდება. გარე ველის ინდუქციის გაზრდით დამაგნიტებული ნივთიერების მაგნიტური ველის ინდუქციაც იზრდება. ძალიან ძლიერ გარე ველში, დომენები, რომელთა საკუთარი მაგნიტური ველი ემთხვევა გარე ველის მიმართულებას, ყველა დანარჩენ დომენს შთანთქავენ იქმნება მაგნიტური გაჯერაბა. ნახ. 4 ფერომაგნიტური ნიმუშის დამაგნიტების პროცესის ილუსტრაციას წარმოადგენს.

 

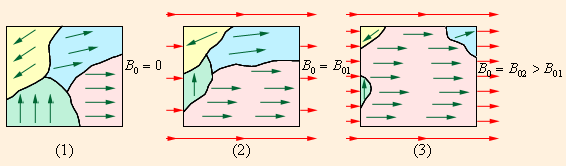
ნახ. 4.

ფერომაგნიტური ნიმუშის დამაგნიტება. (1) B₀ = 0; (2) B₀ = B₀₁; (3) B₀ = B₀₂ > B₀₁