ელექტრომაგნიტური ინდიქციის მოვლენა დიდ ინგლისელი ფიზიკოსის მ.ფარადეის მიერ იქნა აღმოჩენილი 1831 წელს. იგი იმაში მდგომარეობს, რომ ჩაკეტილი გამტარის კონტურის განმჭოლი მაგნიტური ნაკადის დროში ცვლილების შედეგად ამ კონტურში ელექტრული ველი აღიძვრება.
S კონტურის განმჭოლი მაგნიტური Φ ნაკადი ეწოდება სიდიდეს
Φ = B · S · cos α,
სადაც B – მაგნიტური ინდუქციის ვექტორის სიდიდეა, α –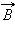 
ვექტორსა და კონტურის სიბრტყის 
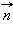მართობს შორის კუთხეა (ნახ. 1).
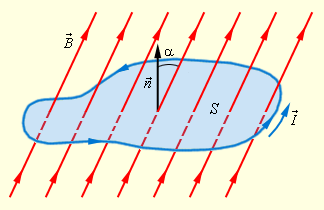
ნახ. 1.
ჩაკეტილი კონტურის გამსჭვალავი მაგნიტური ნაკადი.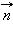 
მართობისა დაკონტურის შემოვლის არჩეული დადებითი მიმართულება 
დაკავშირებულია მარჯვენა ბურღის წესთან
მაგნიტური ნაკადის განმარტება იოლად შეიძლება განზოგადდეს არაერთგვაროვანი მაგნიტური ველისა ან კონტურისათვის, რომელიც ბრტყელი არ არის. სი სისტემაში მაგნიტური ნაკადის ერთეულს ვებერი ეწოდება (ვბ). 1 ვბ-ს ტოლი მაგნიტური ნაკადი იქმნება 1 ტესლა ინდუქციის მაგნიტური ველით, რომელიც 1 მ2 ფართობის ბრტყელი კონტურს განჭოლავს:
1 ვბ = 1 ტს · 1 მ2.
ფარადეიმ ექსპერიმენტულად დაადგინა, რომ მაგნიტური ნაკადის ცვლილებისას გამტარ კონტურში აღიძვრება ინდუქციის ემძ 
ინდ, რომელიც კონტურით შემოსაზღვრულ ზედაპირის განმჭოლავი მაგნიტური ნაკადის ცვლილების სიჩქარის ტოლია მინუს ნიშნით:
ეს ფორმულა ფარადეის კანონის სახელითაა ცნობილი.
ცდები უჩვენებენ, რომ ჩაკეტილ კონტურში მისი განმჭოლი მაგნიტური ნაკადის ცვლილებისას აღძრული ინდუქციური დენი, ყოველთვის ისეა მიმართული, რომ მის მიერ შექმნილი მაგნიტური ველი ხელს უშლის ინდუქციური დენის გამომწვევი მაგნიტური ნაკადის ცვლილებას. ეს მტკიცებულობა, ფორმულირებული 1833 წელს, ლენცისწესის სახელითაა ცნიბილი.
ნახ. 2-ზე ერთგვაროვან მაგნიტურ ველში, რომლის ინდუქციის სიდიდე იზრდება დროში, მოთავსებული უძრავი გამტარის კონტურის მაგალითზე ლენცის წესია ილუსტრურებული.
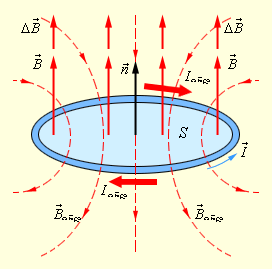
ნახ. 2.
ლენცის წესის ილუსტრაცია. ამ მაგალითში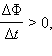 
ხოლო ინდ < 0. ინდუქციური დენი Iინდ მიემართება კონტურის შემოვლის 
მიმართულების შესახვედრად
ლენცის წესი იმ ექსპერიმენტულ ფაქტს ასახავს, რომ ინდ და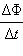 
ყოველთვის ურთიერთსაწინააღმდეგო ნიშნები აქვთ (ნიშანი „მინუსი“ ფარადეის ფორმულა). ლენცის წესს ღრმა ფიზიკური არსი აქვს - ის გამოსახავს ენერგიის შენახვის კანონს.
ჩაკეტილი კონტურის განმჭოლი მაგნიტული ნაკადის ცვლილება შეიძლება ორი მიზეზით ხდებოდეს.
1. მაგნიტური ნაკადი იცვლება კონტურის ან მისი ნაწილების დროში მუდმივ მაგნიტურ ველში გადაადგილების შედეგად. ეს შემთხვევაა, როცა გამტარი და მასთან ერთად მუხტის თავისუფალი მატარებლები მაგნიტურ ველში მოძრაობენ. ინდუქციის ემძ გამტარში მოძრავ თავისუფალ მუხტებზე ლორენცის ძალის მოქმედებით აღიძვრება. ლორენცის ძალა ამ შემთხვევაში იგივე როლს თამაშობს რასაც გვერდითი ძალები.
მაგალითის სახით განვიხილოთ თუ როგორ აღიძვრება ინდუქციის ემძ მართკუთხა კონტურში, რომელიც კონტურის სიბრტყის მართობულ ერთგვაროვან მაგნიტურ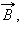 
ველშია მოთავსებული. ვთქვათ კონტურის l სიგრძის ერთ-ერთი გვერდი სხვა ორ გვედზე სრიალებს 
სიჩქარით (ნახ. 3).
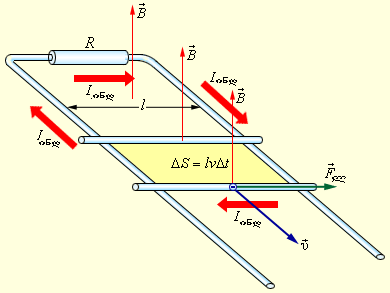
ნახ. 3.
ინდუქციის ემძ-ის აღძვრა მოძრავ გამტარში. თავისუფალ ელექტრონზე მომქმედი ლორენცის ძალის მდგენელია მითითებული
თავისუფალ მუხტებზე კონტურის ამ უბანზე მოქმედებს ლორენცის ძალა. ამ ძალის ერთ-ერთი მდგენელი, რომელიც მუხტის გადატანით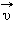 
სიჩქარესთანაა დაკავშირებული, მიმართულია გამტარის გასწვრივ. ეს მდგენელი ნახ. 3-ზეა მითითებული. მისი სიდიდე ტოლია
Fლ = eυB
l გზაზე Fლ ძალის მუშაობა ტოლია
A = Fლ · l = eυBl.
განმარტების მიხედვით ემძ
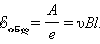
კონტურის სხვა, უძრავ გვერდებში გვერდითი ძალა ნულის ტოლია. გამოსახულებას ინდ -სათვის შეიძლებას მიეცეს ჩვეული სახე. Δt დროის განმავლობაში კონტურის ფართობი იცვლება ΔS = lυΔt-ით. ამავე დროში მაგნიტური ნაკადის ცვლილება ტოლია ΔΦ = BlυΔt. აქედან გამომდინარე,
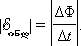
ინდ-სა და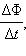 
დამაკავშირებელ ფორმულაში ნიშნის დასადგენად, უნდა აირჩეს მარჯვენა ბურღის წესით ერთმანეთთან შეთანხმებული, 
მართობის მიმართულება და კონტურის შემოვლის დადებითი მიმართულება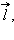 
, ისე როგორც ნახ. 1 და 2-ზეა მოცემული. ასე ადვილად მივალთ ფარადეის ფორმულასთან.
თუ მთელი წრედის წინაღობა R-ის ტოლია, მაშინ მასში გამავალი ინდუქციური დენი ტოლია
Iინდ = ინდ/R.
Δt დროში R წინაღობაზე გამოყოფილი ჯოულის სითბო ტოლია
ისმის კითხვა: ლორენცის ძალა მუშაობას არ ასრულებს და მაშინ საიდან მოდის ეს ენერგია! ეს პარადოქსი იმიტომ წარმოიქმნება, რომ ჩვენ გავითვალისწინეთ ლორენცის ძალის მხოლოდ ერთი მდგენელი. მაგნიტურ ველში მოთავსებულ გამტარში ინდუქციური დენის გავლისას თავისუფალ მუხტებზე მოქმედებს ლორენცის ძალა, რომელიც გამტარის გასწვრის მუხტების მიძრაობის ფარდობით სიჩქარესთანაა დაკავშირებული. ეს მდგენელი ამპერის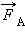 
ძალის გამოვლინებაზეა პასუხისმგებელი. ნახ. 3-ზე გამოსახული შემთხვევისათვის ამპერის ძალის სიდიდე ტოლია FA= I B l. ამპერის ძალა მიმართულია გამტარის მოძრაობის შემხვედრი მიმართულებით; ამიტომ ის ასრულებს უარყოფისთ მექანიკურ მუშაობას. Δt დროში Aმექ მუშაობა ტოლია
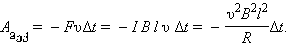
მაგნიტურ ველში მოძრავი გამტარი, რომელშიც ინდუქციური დენი გადის, მაგნიტურ დამუხრუჭებას განიცდის. ლორენცის ძალის სრული მუშაობა ნულის ტოლია. კონტურში ჯოულის სითბო გამოიყოფა ან გარე ძალის მუშაობით, რომელიც უზრუნვეყოფს გამტარის სიჩქარის მუდმივობას, ან გამტარის კინეტიკური ენერგიის შემცირების ხარჯზე.
2. კონტურის განმჭოლი მაგნიტური ნაკადის ცვლილების მეორე მიზეზია უძრავი კონტურის შემთხვევაში მაგნიტური ველის ცვლილება დროში. ამ დროს ინდუქციის ემძ აღძვრა უკვე არ შეიძლება აიხსნას ლორენცის ძალის მოქმედებით. უძრავ გამტარში ელექტრონების მიძრაობაში მოყვანა მხოლოს ელექტრულ ველს შეუძლია. ეს ელექტრული ველი დროში ცვალებადი მაგნიტური ველის საშუალებით იშვება. ჩაკეტილ კონტურში ერთეულოვანი დადებითი მუხტის გადაადგილებისას ამ ველის მუშაობა უძრავ გამტარში ინდუქციის ემძ-ს ტოლია. აქედან გამომდინარე, მაგნიტური ველის ცვლილებით მიღებული ელექტრული ველი არ არის პოტენციური. მას გრიგალურ ელექტრულ ველს უწოდებენ. წარმოდგენა გრიგალურ ელექტრულ ველზე ფიზიკაში ინგლისელმა ფიზიკოსმა ჯ.მაქსველმა ჯ.მაქსველმა შემოიტანა 1861 წელს.
უძრავ გამტარში ელექტრომაგნიტური ინდუქციის მოვლენაც, რომელიc გარემომცველი მაგნიტური ველის ცვლილებისას აღიძვრება ისევ ფარადეის ფორმულით აღიწერება. ამგვარად, ინდუქციის მოვლენა მოძრავ და უძრავ გამტარებში ერთნაერად მიმდინარეობს, მაგრამ ინდუქციური დენის გამომწვევი ამ ორი შემთხევებისათვის სხვადსხვაა: მოძრავი გამტარის შემთხვევაში ინდუქციის ემძ ლორენცის ძალითაა განპირობებული; უძრავი გამტარისათვის ინდუქციის ემძ-ს მიზეზი თავისუფალ ელექტრონებზე, მაგნიტური ველის ცვლილებით აღძრული, გრიგალირი ელექტრული ველის მოქმედების შედეგია.