{loadnavigation}
არაერთგვაროვანი უბნების შემცველი რთული ელექტრული წრედების გათვლის გასამარტივებლად გამოიყენება კირხოფის წესი, რომელიც ომის კანონის განზოგადოებაა განშტოებული წრედებისათვის.
განშტოებულ წრედებში შეიძლება გამოვყოთ საკვანძო წერტილები (კვანძები), რომლებშიც შედის არანაკლებ სამი გამტარისა (ნახ. 1). კვანძებში შემავალი დენები მიღებულია ჩაითვალოს დადებითად; კვანძიდან გამომავალი კი უარყოფითად.
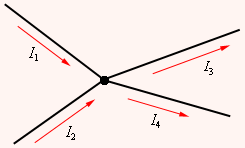
ნახ. 1.
ელექტრული წრედის კვანძი. I1, I2 > 0; I3,I4 < 0
მუდმივი დენის წრედის კვანძში არ შეიძლება ხდებოდეს მუხტის დაგროვება. აქედან გამომდინარეობს კირხოფის პირველი წესი:
განშტოებული წრედის ყოველი კვანძისათვის დენის ძალების ალგებრული ჯამი ნულის ტოლია:
I1 + I2 + I3 + ... + In = 0.
კირხოფის პირველი წესი ელექტრული მუხტის შენახვის კანონის შედეგს წარმოადგენს.
განშტოებულ წრედში შეიძლება გამოიყოს ერთგვაროვანი და არაერთგვაროვანი უბნებისაგან შედგენილი ჩაკეტილი გზების გარკვეული რაოდენობა. ასეთ ჩაკეტილ გზებს კონტურებს უწოდებენ. გამოყოფილი კონტურის სხვადასხვა უბანში შეიძლება გადიოდეს სხვადსხვა დენი. ნახ. 2-ზე უბრალო განშტოებული წრედის მაგალითია წარმოდგენილი. წრედი ორ a და d კვანძს შეიცავს, რომლებშიც ერთნაირი დენი შედის; ამიტომ მათგან მხოლოდ ერთი არის დამოუკიდებელი (a ან d).
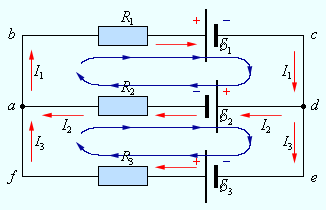
ნახ. 2.
უბრალო განშტოებული წრედის მაგალითი. წრედი ერთ დამოუკიდებელ კვანძს (a ან d) და ორ დამოუკიდებელ კონტურს შეიცავს (მაგალითად,abcd და adef)
წრედში შეიძლება გამოიყოს სამი კონტური abcd, adef და abcdef. მათგან მხოლოდ ორია დამოუკიდებელი (მაგალითად,, abcd და adef), რადგანაც მესამე არ შეიცავს არანაირ ახალ უბანს.
კიტხოფის მეორე წესი ომის განზოგადოებული კანონის შედეგს წარმოსდგენს.
ჩავწეროთ ომის განზოგადოებული კანონი 2-ზე წარმოდგენილი წრედის ერთ-ერთი კონტურის შემადგენელი უბნისთვის, მაგალითად, abcd-სათვის. ამისათვის ყოველი უბნისთვის უნდა მივუთითოთ დენის დადებითი მიმართულება და კონტურის შემოვლის დადებითი მიმართულება. ომის განზოგადოებული კანონის ჩაწერისას ყოველი უბნისთვის აუცილებელია დაცული იქნეს გარკვეული „აღნიშვნების წესი“,რომელიც ნახ. 3-ზე არის განმარტებული.
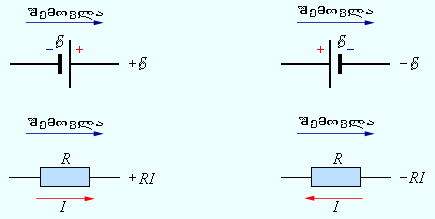
ნახ. 3.
„აღნიშნების წესი“
abcd კონტურისთვის ომის განზოგადოებული კანონი ჩაიწერება შემდეგი სახით:
bc უბნისათბის: I1R1 = Δφbc –  1.
1.
da უბნისათბის: I2R2 = Δφda –  2.
2.
თუ ამ ტოლობების მარჯვენა და მარცხენა მხარეების შევკრებთ და გავითვალისწინებთ, რომ Δφbc = – Δφda , მივიღებთ:
I1R1 + I2R2 = Δφbc + Δφda –  1 +
1 +  2 = –
2 = – 1 –
1 –  2.
2.
ანალოგიურად, adef კონტურისათვის შეიძლება ჩაიწეროს:
– I2R2 + I3R3 =  2 +
2 +  3.
3.
კირხოფის მეორე წესი შეიძლება ასე ჩამოვაყალიბოთ: მუდმივი დენის ნებისმიერი განშტოებული წრედის ყოველი ჩაკეტილი კონტურის წინაღობის ამ უბნის დენის ძალაზე ნამრავლების ალგებრული ჯამი ტოლია ამ კონტურის გასწვრის ემძ-ს ალგებრული ჯამისა.
განშტოებული წრედის ყველა დამოუკიდებელი კვანძებისა და კონტურებისთვის ჩაწერილი კირხოფის პირველი და მეორე წესების ერთობლიობა იძლევა ელექტრული წრედისთვის ძაბვებისა და დენის ძალების გათვლისთვის აუცილებელ და საკმარის ალგებრულ განტოლებათა რაოდენობას. ნახ. 2-ზე მოცემული წრედისათვის, სამი უცნობი I1, I2 და I3 დენის ძალის განსაზღვრისათვის განტოლებათა სისტემას აქვს სახე:
I1R1 + I2R2 = –  1 –
1 –  2,
2,
– I2R2 + I3R3 =  2 +
2 +  3,
3,
– I1 + I2 + I3 = 0.
ამგვარდ, კირხოფის წესს განშტოებული წრედის გათვლები დაჰყავს წრფივი ალგებრული სისტემის ამიხსნამდე. ამ განტოლებათა სისტემის ამოხსნა რაიმე პრიციპულ სირთულეს არ წარმოადგენს, მაგრამ ხანდახან ძალიან გრძელია უბრალო წრედების შემთხვევაშიც. თუ ამოხსნის შედეგად რომელიმე უბანზე დენის ძალა უარყოფითი აღმოჩნდება, ეს იმაზე მიუთითებს, რომ დენი ამ უბანზე მოძრაობს აღებული დადებითი მიმართულიბის საწინააღმგეგოდ.
{loadnavigation}
ელექტრულ წრედში გამტარები შეიძლება იყვნენ შეერთებული მიმდევრობით და პარალელურად.
გამტარების მიმდევრობითი შეერთებისას (ნახ. 1) დენის ძალა ყველა გამტარში ერთნაერია:
I1 = I2 = I.

ნახ. 1.
გამტარების მიმდევრობითი შეერთება
ომის კანონის თანახმად გამტარებზე U1 და U2 ტოლია
U1 = IR1, U2 = IR2
ორივე გამტარზე U სრული ძაბვა U1 და U2 ძაბვების ჯამის ტოლია:
U = U1 + U2 = I(R1 + R2) = IR,
სადაც R –მთელი წრედის ელექტრული წინაღობაა. აქედან გამოდის:
R = R1 + R2.
გამტარების მიმევრობითი შეერთებისას წრედის სრული წინაღობა ცალკეული გამტარების წინაღობების ჯამის ტოლია.
ეს შედეგი სამართლიანია გამტარების ნებისმიერი რიცხვის მიმდევრობითი შეერთებისთვის.
გამტარების პარალელური შეერთებისას (ნახ. 2) ორივე გამტარზე U1 და U2 ძაბვები ტოლია:
U1 = U2 = U.
ორივე გამტარში გამავალი დენების ჯამი I1 + I2 განუშტოვებელი წრედის დენის ტოლია:
I = I1 + I2.
ეს შედეგი იქიდან გამოდის, რომ მუდმუვი დენის წრედის განშტოების წერტილებში (A და B კვანძები) მუხტი ვერ დაგროვგება. მაგალითად, A კვანძთან Δt დროის განმავლობაში მიდის IΔt მუხტი, ხოლო კვანძიდან იგივე დროში გამოდის I1Δt + I2Δt. აექდან გამომდინარე, I = I1 + I2.

ნახ. 2.
გამტარების პარალელური შეერთება.
ომის კანონის მიხედვით
\(I_{1}=\frac{U}{R_{1}}\), \(I_{2}=\frac{U}{R_{2}}\) და \(I=\frac{U}{R}\)
სადაც R – მთელი წრედის ელექტრული წინაღობაა, მივიღებთ
| \(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\) |
გამტარების პარალელური შეერთებისას წრედის სრული წინაღობის შებრუნებული სიდიდე ტოლია პარალელურად ჩართული გამტარების წინაღობების შებრუნებული სიდიდეების ჯამისა.
ეს შედეგი სამართლიანია გამტარების ნებისმიერი რიცხვის პარალელური შეერთებისთვის.
გამტარების მიმდევრობითი და პარალელური შეერთების ფორმულები ბევრ შემთხვევაში მრავალი რეზისტორისგან შედგენილი რთული წრედის წინაღობის გათვლის საშუალებას იძლევიან. ნახ. 3-ზე ასეთი რთული წრედის მაგალითია მოყვანილი და ნაჩვენებია გათვის თანმიმდევრობა.

ნახ. 3
რთული წრედის წინაღობის გათვლა. ყველა გამტარის წინაღობა მითითებულია ომებში (ომ)
უნდა აღინიშნოს, რომ განსხვავებული წინაღობისგან შედგენი ყველა რთული წრედის გათვლა არ შეიძლება მიმდევრობითი და პარალელური შეერთებების ფორმულების საშუალებით. ნახ. 4-ზე მოყვანილია ელექტრული წრედის მაგალითი, რომლის გათვლა არ შეიძლება ზევით მითითებული მეთოდით.

ნახ. 4.
ელექტრული წრედის მაგალითი არ დაიყვანება გამტარების მიმდევრობითი და პარალელური შეერთებების კომბინაციაზე
ნახ. 4-ზე წარმოდგენილი წრედის მსგავსი წრედები, ისევე როგორც განშტოებული, რამოდენიმე დენის წყაროს შემცველი წრედები კირხოფის წესის საშუალებით გაითვლება.
{loadnavigation}
თუ იზოლირებულ გამტარს \(\vec{E}\) ელექტრულ ველში მოვათავსებთ, მაშინ გამტარის \(q\) თავისუფალ მუხტებზე იმოქმედებს ძალა \(\vec{F}=q\vec{E}\) . ამის შედეგად გამტარში წარმოიქმნება თავისუფალი მუხტების მცირე ხანგრძლივობის გადაადგილება. ეს პროცესი მაშინ შეწყდება, როცა გამტარის ზედაპირზე აღძრული მუხტების საკუთარი ელექტრული ველი გაწონასწორდება გარე ელექტრული ველით. გამტარის შიგნით ელექტროსტატიკური ვეილის ტოლქმედი ნულის ტოილ იქნება. მაგრამ, გამტარებში გარკვეულ პირობებში შეიძლება აღიძრას თავისუფალი ეელქტრული მუხტის მატარებლების მოწესრიგებული მოძრაობა. ასეთ მოძრაობას ელექტრულ დენს უწოდებენ. ელექტრული დენის მიმართულებად მიღებულია დადებითი თავისუფალი მუხტების მიმართული მოძრაობა. გამტარში ელექტრული დენის არსებობისათვის საჭიროა მასში ელექტრული ველის შექმნა.
ელექტრული დენის რაოდენობრივ საზომს დენის ძალა \(I\) წარმოადგენს. იგი სკალარული სიდიდეა, რომელიც ტოლია დროის \(\Delta t\) ინტერვალში გამტარის განივკვეთში გამავალი \(\Delta q\) მუხტის ფარდობისა, დროის ამ ინტერვალთან:
\(I=\frac{\Delta q}{\Delta t}\)
თუ დენის ძალა და მისი მიმართულება დროში არ იცვლება, მაშინ ასეთ დენს მუდმივ დენს უწოდებენ.

ნახ. 1.
მოწესრიგებული მოძრაობა
საერთაშორისო სი სისტემაში დენის ძალა იზომება ამპერებში (ა). საზომი ერთეული 1 ამპერი დადგენილია ორი პარალელური დენიანი გამტარის მაგნიტური ურთიერთქმედებით.
მუდმივი ელექტრული დენი მხოლოდ ჩაკეტილ ელექტრულ ქსელში შეიძლება შეიქმნას, სადაც მუხტის თავისუფალი მატარებლები ცირკულირებენ ჩაკეტილ ტრაექტორიაზე. ასეთი ქსელის ყოველ წერტილში ელექტრული ველი დროში უცვლელია. აქედან გამომდინარე, მუდმივი დენის ქსელში ელექტრულ ველს აქვს გაყინული ელექრული ველის ხასიათი. მაგრამ, ჩაკეტილ ტრექტორიაზე ელექტრულ ველში ელექტრული მუხტის გადაადგილებისას ელექტრული ძალების მუშაობა ნულის ტოლია. ამიტომ მუდმივი დენის არსებობისთვის აუცილებელია ელექტრულ ქსელში ისეთი მოწყობილობის არსებობა, რომელსაც არაელექტრული წარმოშობის ძალების მუშაობის საშუალებით, შეუძლია შექმნას და უზრუნველყოს პოტენციალთა სხვაობის არსებობა. ასეთ მოწყობილობებს მუდმივი დენის წყაროებს უწოდებენ. არაელექტროსტატიკური წარმოშობის ძალებს, რომლებიც მუხტის თავისუფალ მატარებლებზე მოქმედებენ დენის წყაროს მხრიდან, გვერდით ძალებს უწოდებენ.
გვერდითი ძალები შეიძლება სხვადასხვაგვარი იყოს. გალვანურ ელემენტებში ან აკუმულიატორებში ისინი ელექტროქიმიური პროცესების ხარჯზე წარმოიქმნება, ხოლო მუდმივი დენის გენერატორებში გვერდითი ძალები აღიძვრება გამტარების მაგნიტურ ველში მოძრაობისას. დენის წყარო ელექტრულ წრედში იგივე როლს ასრულებს, რასაც ტუმბო, რომელიც აუცილებელია წყლის გადასაქაჩად ჩაკეტილ ჰიდრავლიკურ სისტემაში. გვერდითი ძალების მოქმედებით ელექტრული მუხტები მოძრაობენ დენის წყაროს შიგნით ელექტროსტატიკური ვეილის ძალების საწინააღმდეგოდ, რის ხარჯზეც ელექტრულ წრედს შეუძლია მუდმივი ელექტრული დენის შენარჩუნება.
მუდმივი დენის წრედის გასწვრივ დენის წყაროს შიგნით მომქმედი გვერდითი ძალების მიერ ელექტრული მუხტის გადანაცვლებისას, სრულდება მუშაობა.
ფიზიკური სიდიდეს, რომელიც ტოლია გვერდითი ძალების მიერ q მუხტის დენის წყაროს უარყოფითი პოლუსიდან დადებითი პოლუსამდე გადანაცვლებისას დახარჯული Aგვ მუშაობის ფარდობისა ამ მუხტის სიდიდდესთან, დენის წყაროს ელექტრომამოძრავებელი ძალა ეწოდება (ემძ):

ამგვარად, ემძ განისაზღვრება მუშაობით, რომელიც სრულდება გვერდითი ძალების მიერ ერთეულოვანი დადებითი მუხტის გადაადგილებისას. ელექტრომამოძრავებელი ძალა, ისევე როგორც პოტენციალთა სხვაობა, იზომება ვოლტებში (ვ).
ერთეულოვანი დადებითი მუხტის მუდმივი დენის ჩაკეტილ წრედში გადაადგილებისას გვერდითი ძალების მუშაობა ამ წრედში მომქმედი ემძ ჯამის ტოლია, ხოლო ელექტროსტატიკური ველის მუშაობა ნულის ტოლია.
მუდმივი დენის წრედი შეიძლება დაიყოს ცალკეულ უბნებად. იმ უბნებს სადაც არ მოქმედებენ გვერდითი ძალები (ე.ი. უბნები, რომლების დენის წყაროს არ მოიცავენ), ერთგვაროვანს უწოდებენ. დენის წყაროს შემცველ უბნებს კი, არაერთგვაროვანს.
წრედის გარკვეულ უბანზე ერთეულოვანი დადებითი მუხტის გადაადგილებისას მუშაობას ასრულებენ როგორც ელექტროსტატიკური (კულონური) ძალები, ასევე გვერდითი ძალები. ელექტროსტატიკური ძალების მუშაობა არაერთგვაროვანი უბნის საწყის (1) და საბოლოო (2) წერთილებს შორის პოტენციალთა სხვაობის Δφ12 = φ1 - φ2 ტოლია. გვერდითი ძალების მუშაობა განმარტების მიხედვით, მოცემულ უბანზე მომქმედი ელექტრომამოძრავებელი ძალის  12 ტოლია. ამიტომ, სრული მუშაობა ტოლია
12 ტოლია. ამიტომ, სრული მუშაობა ტოლია
U12 = φ1 - φ2 +  12.
12.
U12 სიდიდეს წრედის 1-2 უბანის დაძაბულობას უწოდებენ. ერთგვაროვანი უბნის შემთხვევაში დაძაბულობა პოტენციალთა სხვაობის ტოლია.
U12 = φ1 - φ2.
1826 წელს გერმანელმა ფიზიკოსმა ომმა ექსპერიმენტულად დაადგინა, რომ ერთგავაროვან მეტალის გამტარში (ე.ი. გამტარში რომელზეც არ მოქმედებენ გვერდითი ძალები) გამავალი დენის ძალა I პროპორციულია გამტარის ბოლოებზე U დაძაბულობისა:
\(I=\frac{U}{R}\) ან \(U=RI\)
სადაც \(R=const\).
R-s ელექტრულ წინაღობას უწოდებენ. ელექტრული წინაღობის მქონე გამტარს რეზისტორი ეწოდება. მოცემული ფორმულა გამოსახავს ომის კანონს წრედის ერთგავაროვანი უბნისათვის: გამტარში დენის ძალა პირდაპირპროპორციულია მასზე მოდებული ძაბვისა და უკუპროპორციულია მისი წინაღობისა.
SI სისტემაში ელექტრული წინაღობის ერთეულს ომი წარმოადგენს. ერთი ომი წინაღობა წრედის ისეთ უბანს აქვს, რომელშიც ერთი ვოლტი ძაბვისას ერთი ამპერერი დენი გადის.
გამტარებს, რომლებიც ომის კანონს ემორჩილებიან წრფივ გამტარებს უწოდებენ.
გამტარებს, რომლებიც ობის კანონს ემორჩილებიან, წრფივს უწოდებენ. I დენის ძალის U ძაბვაზე გრაფიკული დამოკიდებულება (ასეთ გრაფიკებს ვოლტ-ამპერულ მახასიათებლებს უწოდებრნ) კოორდინატთა სათავეზე გამავალი სწორი ხაზის სახით გამოისახება. უნდა აღინიშნოს, რომ არსებობს მრავალი მასალა და მოწყობილობა, რომლების ომის კანონს არ ამორჩილება, მაგალითად, ნახევარგამტარული დიოდი ან აირ-განმუხტვის ნათურა. მეტალურ გამტარებშიც კი, საკმარისად დიდ დენის ძალის შემთხვევაში ომის კანონიდან გადახრა დაიკვირვება, რადგანაც მეტალების ელექტრული წინაღობა ტემპერატურის ზრდისას იძრდება.
ემძ-ს შემცველი წრედის უბნისთვის ომის კანონი შემდეგი სახით ჩაიწერება:
IR = U12 = φ1 - φ2 +  = Δφ12 +
= Δφ12 +  .
.
ამ თანაფარდობას განზოგადოებულ ომის კანონს ან ომის კანონს წრედის არაერთგვაროვანი უბნისათვის უწოდებენ.
ნახ. 2 -ზე მუდმივი დენის ჩაკეტილი წრედია გამოსახული. წრედის (cd) უბანი ერთგვაროვანია.

ნახ. 2.
მუდმივი დენის წრედი
ომის კანონის მიხედვით
IR = Δφcd.
(ab) უბანი  -ს ტოლ ემძ-ს შეიცავს.
-ს ტოლ ემძ-ს შეიცავს.
ომის კანონის მიხედვით არაერთგვაროვანი წრედისათვის,
Ir = Δφab +  .
.
ორივე ტოლობის შეკრებით, ვღებულობთ:
I (R + r) = Δφcd+Δφab+ 
მაგრამ
Δφcd = Δφba = - Δφab. ამიტომ
 |
ეს ფორმილა გამოსახავს ომის კანონს სრული წრედისთვის: დენის ძალა სრული წრედისათვის ტოლია დენის წყაროს ემძ-ს ფარდობისა წრედის ერთგავროვანი და არაერთგვაროვანი წინაღობების ჯამზე.
ნახ. 2-ზე წინაღობა შეიძლება განვიხილოთ როგორც დენის წყაროს შინაგანო წინაღობა. ასეთ შემთხვევაში ნახაზზე (ab) უბანი წყარის შიგა უბანს წარმოადგენს. თუ a და b წერტილებს ისეთი გამტარით შევაერთებთ, რომლის წინაღობა მცირეა წყაროს შიგა წინაღობასთან შედარებით (R << r), მაშინ წრედში მოკლე ჩართვის დენი გაივლის

მოკლე ჩართვის დენის ძალა ის მაქსიმალური დენის ძალაა, რომლის მიღებაც ელექტრომამოძრავებელი ძალისა და r შინაგანი წინაღობის დენის წყაროსაგან შეიძლება. მცირე შიგა წინაღობის მქონე წყაროებში მოკლე ჩართვის დენი შეიძლება იყოს ძალიან დიდი და გამოიწვიოს ელექტრული წრედის ან წყაროს გარღვევა. მაგალითად, ავტომობილებში გამოყენებულ ტყვიის აკუმულატორებში მოკლე ჩართვის დენის ძალა რამოდენიმე ასეულ ამპერს შეიძლება შეადგენდეს. მოკლე ჩართვა განსაკუთრებით განათების ქსელშია საშიში, რომელიც ქვესადგურიდან (ათასობით ამპერი) იკვებება. ასეთი დიდი დენების დამანგრეველი მოქმედების თავიდან ასაცილებლად წრედში სპეციალურ დამცველებს იყენებენ ან წრედის დაცვის ავტომატების ჩართვა ხდება.
ზოგ შემთხვევაში მოკლე ჩართვის დენის ძალის საშიში მნიშვნელობებისგან თავის დასაღწევად წყაროსთან მიმდევრობით რთავენ რაღაც წინაღობას. მაშინ r წინაღობა შიგა და გარე წინაღობების ჯამის ტოლია, და ასეთ შემთხვევაში მოკლე ჩართვის დენის ძალა არ აღმოჩნდება ძალიან დიდი.
თუ გარე წრედი გახსნილია, მაშინ Δφba = - Δφab =  , ე.ი. ბატარეის ბოლოებზე პოტენციალთა სხვაობა ემძ-ს ტოლია.
, ე.ი. ბატარეის ბოლოებზე პოტენციალთა სხვაობა ემძ-ს ტოლია.
თუ ჩართულია R გარე დატვირთვის წინაღობა და ბატარეაში გადის I დენი, მის პოლუსებზე პოტენციალთა სხვაობა ხდება Δφba =  - IR -ის ტოლი.
- IR -ის ტოლი.
ნახ. 3-ზე მოცემულია მუდმივი დენის წყარო  -ს ტოლი ემძ-თი და r წინაღობით სამ რეჟიმში: „უქმი სვლა“, მუშაობა დატვირთვაზე და მოკლე ჩართვის რეჟიმი. მითითებულია ბატარეის შიგნით ელექტრული ველის დაძაბულობა და დადებით მუხტებზე მომქმედი ძალები: \(\vec{F}\)ე - ელექტრული ძალა და \(\vec{F}\)გვ - გვერდითი ძალა. მოკლე ჩართვის რეჟიმში ელექტრული ველი ბატარეის შიგნით ქრება.
-ს ტოლი ემძ-თი და r წინაღობით სამ რეჟიმში: „უქმი სვლა“, მუშაობა დატვირთვაზე და მოკლე ჩართვის რეჟიმი. მითითებულია ბატარეის შიგნით ელექტრული ველის დაძაბულობა და დადებით მუხტებზე მომქმედი ძალები: \(\vec{F}\)ე - ელექტრული ძალა და \(\vec{F}\)გვ - გვერდითი ძალა. მოკლე ჩართვის რეჟიმში ელექტრული ველი ბატარეის შიგნით ქრება.

ნახ. 3.
მუდმივი დენის წყარის სქემატური გამოსახულება: 1 - ბატარეა ღიაა; 2 - ბატარეა შეერთებულია გარე R წინაღობასთან; 3 - მოკლე ჩართვის რეჟიმი
მუდმივი დენის წრედში დაძაბულობისა და დენების გაზომვისათვის გამოიყენევა სპეციალური ხელსაწყოები - ვოლტმეტრი და ამპერმეტრი.
ვოლტმეტრი მომჭერებზე მოდებული პოტენციალთა სხვაობის გასაზომადაა განკუთვნილი. იგი წრედში, რომელზეც იზომება პოტენციალთა სხაობა, პარალელურად ირთვება. ნებისმიერ ვოლტმეტრს აქვს გარკვეული შიგა წინაღობა Rვ. იმისათვის, რომ ვოლტმეტრმა გასაზომ წრედში არ გამოიწვიოს დენების მნიშვნელოვანი გადანაწილება, მისი საკუთარი წინაღობა უნდა დიდ იყოს იმ წრედის უბნის წინაღობაზე, რომელშიაც იგია ჩართული. ნახ. 4-ზე გამოსახული წრედისათვის ეს პირობა ასე ჩაიწერება:
Rვ >> R1.
ეს პირობა ნიშნავს, რომ ვოლტრმეტრში გამავალი დენი Iვ = Δφcd / Rვ, ბევრად ნაკლებია წრედის გასაზომ უბანში გამავალ დენზე I = Δφcd / R1.
რადგან ვოლტმეტრის შიგnით გვერდითი ძალები არ მოქმედებენ, პოტენციალთა სხაობა მის მომჭერებზე განმარტების მიxედვით ძაბვას ემთხვევა. ამიტომ ითვლება, რომ ვოლტმეტრი ძაბვას ზომავს.
ამპერმეტრი წრედში დენის ძალის გასაზომად გამოიყენება. ამპერმეტრი წრედში მიმდევრობით ირთვება, იმისთვის, რომ მასში მთელმა გასაზომმა დენმა გაიაროს. ამპერმეტრსაც აქვს გარკვეული შიგა წინაღობა RA. ვოლტმეტრისაგან განსხვავებით, ამპერმეტრის შიგა წინაღობა საკმარისად მცირე უნდა იყოს მთელი წრედის წინაღობასთან შედარებით. ნახ. 4 -ზე გამოსახული წრედისთვის ამპერმეტრის წინაღობა უნდა აკმაყოფილებდეს პირობას
RA << (r + R1 + R2),
იმისათვის რომ ამპერმეტრის ჩართვის დენი წრედში არ შეიცვალოს.

ნახ. 4.
(А) ამპერმეტრისა და (ვ) ვოლტმეტროს ჩართვა წრედში
{loadnavigation}
გამოცდილება უჩენებს, რომ დამუხტულ კონდენსატორს აქვს ენერგიის მარაგი.
დამუხტული კონდენსატორის ენერგია ტოლია, კონდენსატორის დასამუხტად საჭირო გარე ძალების მუშაობისა.
კონდენსატორის დამუხტვის პროცესი შეიძლება წარმოვიდგინოთ, როგორც ერთი შემონაფენიდან მეორეზე მუხტის საკმარისად მცირე \(\Delta q> 0\) პორციების მიმდევრობითი გადატანა (ნახ. 1). ამ დროს ერთი შემონაფენი თანდათან იმუხტება დადებითი მუხტით, ხოლო მეორე უარყოფითით. რადგანაც ყოველი პორცია გადაიტანება ისეთ პირობებში, როცა შემონაფენებზე უკვე არის გარკვეული \(q\) მუხტი, ხოლო მათ შორის არის გარკვეული პოტენციალთა სხვაობა \(U=\frac{q}{C}\), ყოველი \(\Delta q\) პორციის გადატანისას გარე ძალები უნდა ასრულებდნენ მუშაობას
\(\Delta A=U\Delta q=\frac{q\Delta q}{C}\) .
Q დამუხტული \(C\) ტევადობის კონდენსატორის \(W_{e}\) ენერგია, შეიძლება იქნეს ნაპოვნი ამ გამოსახულების 0-დან Q-მდე საზღვრებში ინტეგრირებით:
\(W_{e}=A=\frac{Q^{2}}{2C}\)

ნახ. 1. კონდენსატორის დამუხტვის პროცესი
დამუხტული კონდენსატორის ენერგიის გამომსახველი ფორმულა \(Q=CU\) თანაფარდობის გამოყენებით შეიძლება სხვა, ექვივალენტური ფორმით გადაიწეროს.
\(W_{e}=\frac{Q^{2}}{2C}=\frac{CU^{2}}{2}=\frac{QU}{2}\)
ელექტრული \(W_{e}\) ენერგია დამუხტულ კონდენსატორში თავმოყრილ პოტენციურ ენერგიად უნდა განვიხილოთ. \(W_{e}\) ფორმულები დეფორმირებული ზამბარის Eр პოტენციურ ენერგიის ანალოგიურია
\(E_{p}=\frac{kx^{2}}{2}=\frac{F^{2}}{2k}=\frac{Fx}{2}\)
სადაც \(k\) - ზამბარის სიხისტეა, \(x\) - დეფორმაცია, \(F=kx\) - გარე ძალა.
თანამედროვე წარმოდგენების თანახმად, კონდენსატორის ელექტრული ენერგია თავმოყრილია შემონაფენებს შორის სივრცეში, ე.ი. ელექტრულ ველში. ამიტომაც მას ელექტრული ველის ენერგიეს უწოდებენ. ეს ადვილი საჩვენებელია დამუხტული ბრტყელი კონდენსატორის მაგალითზე.
ბრტყელ კონდენსატორში ერთგვაროვანი ველის დაძაბულობა ტოლია \(E=U/d\), მისი ტევადობა კი - \(C=\frac{\varepsilon _{0}\varepsilon S}{d}\). ამიტომ
\(W_{e}=\frac{CU^{2}}{2}=\frac{\varepsilon _{0}\varepsilon SE^{2}d^{2}}{2d}=\frac{\varepsilon _{0}\varepsilon SE^{2}}{2}V\)
სადაც \(V=Sd\) - ელექტრული ველით შევსებულ, შემონაფენებს შორის სივრცის მოცულობაა. ამ ფორმულიდან გამომდინარეობს, რომ ფიზიკური სიდედე
\(w_{e}=\frac{\varepsilon _{0}\varepsilon SE^{2}}{2}\)
სივრცის ერთეულ მოცულიბაზე შექმნილი ელექტრული ველის ელექტრულ (პოტენციურ) ენერგიას წარმოადგეს. მას ელექტრული ენერგიეს მოცულობით სიმკვრივეს უწოდებენ.
სივრცეში ელექტრული მუხტების ნებისმიერი განაწილებით მიღებული ველის ენერგია შეიძლება იქნეს ნაპოვნი მათ მიერ შექმნილი ელექტრული ვეილს მთელ მოცულობაზე მოცულობითი \(w_{e}\) სისმკვრივეების ინტეგრირების საშუალებით.
