{loadnavigation}
მყარ სხეულებში – ამორფულშიც და კრისტალურშიც – ნაწილაკები (მოლეკულები, ატომები, იონები) ასრულებენ სითბურ რხევას წონასწორობის მახლობლად, სადაც მათი ურთიერთქმედების ენერგია მინიმალურია. ნაწილაკებს შორის მანძილის გაზრდისას აღიძვრება მიზიდულობის ძალები, შემცირებისას – განზიდვის ძალები. ნაწილაკებს შორის ურთიერთქმედების ძალები განსაზღვრავენ მყარი სხეულის მექანიკურ თვისებებს.
მყარი სხეულის დეფორმაცია გარე ძალების მოქმედებით მყარი სხეულის ნაწილაკებს შორის განლაგებისა და მანძილების ცვლილების შედეგია.

დეფორმაციის რამოდენიმე სახე არსებობს. ზოგი მათგანი წარმოდგენილია ნახ. 1-ზე.
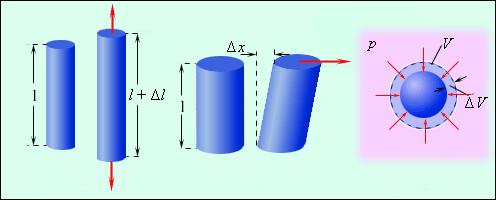
ნახ. 1.
მყარი სხეულებისდეფორმაციის ზოგიერთი სახე: 1 – გაჭიმვის დეფორმაცია; 2 – წანაცვლების დეფორმაცია; 3 – ყოველმხრივი გაჭიმვის დეფორმაცია
დეფორმაციის უმარტივეს სახეს გაჭიმვის დეფორმაცია წარმოადგენს. იგი შეიძლება დავახასიათოთ, როგორც \(\vec{F}\) გარე ძალის მოქმედებით წარმოქმნილი აბსოლუტური \(\Delta l\) წაგრძელება ან შეკუმშვა. \(\Delta l\) და \(F\) შორის კავშირი დამოკიდებულია არა მარტო ნივთიერების მექანიკურ თვისებებზე, არამედ სხეულის გეომეტრიულ ზომებზეც (სისქესა და სიგრძეზე).
აბსოლუტური \(\Delta l\) წაგრძელების შეფარდებას ნიმუშის საწყის \(l\) სიგრძესთან \(\varepsilon\)-ს ფარდობით წაგრძელებას ან ფარდობით დეფორმაციას უწოდებენ
\(\varepsilon =\frac{\Delta l}{l}.\)
გაჭიმვისას \(\varepsilon >0\), შეკუმშვისას \(\varepsilon <0\).
თუ გამჭიმავი გარე ძალის მიმართულებას დადებითად მივიღებთ, მაშინ \(F>0\) გაჭიმვის დეფორმაციისთვის და \(F<0\) – შეკუმშვისათვის. გარე ძალის \(F\) ფარდობას სხეულის განივკვეთის \(S\) ფართობთან მექანიკურ დაძაბულობას უწოდებენ:
\(\sigma=\frac{F}{S}.\)
მექანიკური დაძაბულობის ერთეულად \(Si\) სიტემაში მიღებულია პასკალი. მექანიკური დაძაბულობა წნევის ერთეულებში იზომება.
\(\varepsilon\) და \(\sigma\) სიდიდეებს შორის დამოკიდებულება მყარი სხეულების მექანიკური თვისებების ერთერთ უმნიშვნელოვანეს მახასიათებელს წარმოადგენს. ამ დამოკიდებულების გრაფიკს გაჭიმვის დიაგრამას უწოდებენ. აბსცისთა ღეძზე აღებულია ფარდობითი წაგრძელება \(\varepsilon\), ორდანატაზე – მექანიკური დაძაბულობა \(\sigma\). ნახ. 2-ზე წარმოდგენილია გაჭიმვის დიაგრამის ტიპური მაგალითი მეტალებისთვის (სპილენძი და რბილი რკინა).
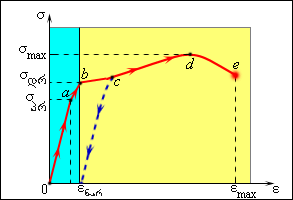
ნახ. 2.
პლასტიკური მასალის ტიპური გაჭიმვის დიაგრამის. ცისფერი ზოლი - დრეკადი დეფორმაციის არეა
მცირე (1 %-ზე საგრძნობლად ნაკლები) დეფორმაციებისთვის \(\sigma\) და \(\varepsilon\) კავშირი წრფივია (Oa მონაკვეთი დიაგრამაზე). ამ შემთხვევაში დაძაბულობის მოხსნისას დეფორმაცია ქრება. ასეთ დეფორმაციას დრეკადს უწოდებენ. σ = σპრ მაქსიმალური მნიშვნელობა, რომლისათვისაც წრფივი კავშირი არ ირღვევა \(\sigma\) და \(\varepsilon\) შორის, პროპორციულობის ზღვარს უწოდებენ (a წერტილი). წრფივ უბანზე სრულდება ჰუკის კანონი:
\(\varepsilon=\frac{1}{E}\sigma.\)
\(E\) კოეფიციენტს იუნგის მოდულს უწოდებენ.
დაძაბულობის შემდგობი გადიდებისას \(\sigma\) და \(\varepsilon\) – ს შორის კავშირი არაწრფივია (ab უბანი). დაძაბულობის მოხსნისას დეფორმაცია პრაქტიკულად მთლიანად ქრება, ე.ი. სხეული აღიდგენს თავის ზომებს. მაქსიმალურ დაძაბულობას ამ უბანზე ზღვრული დრეკადობა ეწოდება. თუ σ > σდაჭ, მაშინ დაძაბულობის მოხსნის მერე ნიმუში საწყის ზომებს ვერ აღიდგენს და სხეული ინარჩუნებს ნარჩენ დეფორმაციას. ასეთ დეფორმაციას პლასტიკურს უწოდებენ (bc, cd და de უბნები). bc უბანზე დეფორმაცია თითქმის დაძაბულობის გაზრდის გარეშე ხდება. ამ მოვლენას მასალის დენადობა ეწოდება. d წერტილში ის უდიდესი დაძაბულობა σmax მიიღწევა, რომელსაც მოცემულ მასალას შეუძლია გაუძლოს (სიმტკიცის ზღვარი). e წერტილში მასალის რღვება ხდება. იმ მასალებს, რომლებისთვისაც გაჭიმვის დიაგრამას აქვს ნახ. 2 სახე პლასტიკურს უწოდებენ. ასეთი მასალების ჩვეულებრივი εmax დეფორმაცია, რომლის დროსაც მასალის რღევა ხდება ათეულობით აღემატება დრეკადი დეფორმაციის უბნის სიგანეს. ასეთ მასალებს მრავალი მეტალი მიეკუთვნება.
იმ მასალებს, რომლებისთვისაც რღვევა ხდება როცა დეფორმაცია დრეკადი დეფორმაციის უბანს ოდნავ აჭარბებს, მყიფეს უწოდებენ (მინა, ფაიფური, თუჯი).
ანალოგიურ კანონზომიერებას ემორჩილება წანაცვლების დეფორმაციაც (ნახ. 1(2)). ამ შემთხვევაში ძალის ვექტორი \(\vec{F}\)მიმართულია ნიმუშის მხების გასწვრივ. ფარდობითი დეფორმაცია განისაზღვრება უგანზომილებო ფარდობით \(\frac{\Delta x}{l}\), ხოლო დაძაბულობა- ფარდობით \(\frac{F}{S}\) (ზედაპირის ერთეულზე მომქმედი ძალა). მცირე დეფორმაციებისათვის
\(\frac{\Delta x}{l}=\frac{1}{G}\frac{F}{S}.\)
ამ თანფარდობაში პროპორციულობის \(G\) კოეფიციენტს წანაცვლების მოდულს უწოდებენ. წანაცვლების მოდული მყარი მასალის უმრავლესობისათვის 2-3-ჯერ ნაკლებია იუნგის მოდულზე. მაგალითად, სპილენძისათვის E = 1,1·1011 ნ/მ2, G = 0,42·1011 ნ/მ2. უნდა გვახსოვდეს, რომ თხევადი და აირადი ნივთიერებისთვის წანაცვლების მოდული ნულის ტოლია.
ნახ. 1.(3)-ზე სითხეში ჩაძირული სხეულის ყოველმხრივი შეკუმშვის დეფორმაციაა მოცემული. ამ შემთხვევაში მექანიკური დაძაბულობა სითხეში p წნევის ტოლია. ფარდობითი დეფორმაცია განისაზღვრება როგორც მოცულობის \(\Delta V\) ცვლილების ფარდობა საწყის მოცულობასთან. მცირე დეფორმაციებისას
\(\frac{\Delta V}{V}=\frac{1}{B}p.\)
ამ ფორმულაში პროპორციულობის კოეფიციენტს ყოველმხრივი შეკუმშვის მოდულს უწოდებენ.
ყოველმხრივი შეკუმშვა შეიძლება განიცადოს არა მხოლოს მყარმა სხეულმა, არამედ სითხეებმა და აირებმაც. წყლისთვის B = 2,2·109 ნ/მ2, ფოლადისთვის B = 1,6·1011 ნ/მ2. წყნარი ოკიანის ფსკერზე, დაახლოებით 4 კმ სიღრმის დონეზე, წნევა დაახლოებით 4·107 ნ/მ2.
ამ პირობებში წყლის მოცულობის ფარდობითი ცვლილება \(\frac{\Delta V}{V}\) 1,8 % შეადგენს, მაშინ როცა ფოლადის სხეულისათვის იგი მხოლოდ 0,025 %-ია, ე.ი. 70-ჯერ ნაკლები. მყარი სხეულები, მათი კრისტალური მესერებით, გაცილებით ნაკლებად კუმშვადია სითხეებთან შედარებით, რომელთა ატომები და მოლეკულები ნაკლებად არიან დაკავშირებული მეზობლებთან. აირების კუმშვადობა მრავალი რიგით უფრო დიდია სითხეებისა და მყარი სხეულების კუმშვადობაზე.
ყოველმხრივი შეკუმშვის მოდულის სიდიდე მოცემულ ნივთიერებაში ბგერის სიჩქარით განისაზღვრება.
{loadnavigation}
ფიზიკური თვისებებისა და მოლეკულური სტრუქტურის მიხედვით მყარი სხეულები ორ კლასად იყოფიან – ამორფული და კრისტალური.
ამორფული სხეულების დამახასიათებელ თავისებურებას მათი იზოტროპულობა წარმოადგენს, ე.ი. ნებისმიერი ფიზიკური თვისება (მექანიკური, ოპტიკური და სხვა) არ არის დამოკიდებული გარე ზემოქმედების მიმართულებაზე. ამორფულ მყარ სხეულებში მოლეკულები და ატომები ქაოტურადაა განლაგებული, ქმნიან რამოდენიმე ნაწილაკისგან შედგენილ მცირე ლოკალურ ჯგუფებს (ახლო წესრიგი). აგებულების მიხედვით ამორფული სხეულები ძალიან ახლოს არიან სითხეებთან. ამორფული სხეულების მაგალითად შეიძლება გამოდგეს მინა, სხვადასხვა გამაგრებული ფისი (ქარვა), პლასმასები და სხვა. თუ ამორფულ სხეულებს გავათბობთ, ის ნელნელა დარბილდება და თხევად მდგომარეობაში გადასვლა იკავებს ტამპერატურის მნიშვნელოვან ინტერვალს.
კრისტალურ სხეულებში ნაწილაკების განლაგება მკაც წესრიგს ემორჩილება, სხეულის მთელ მოცულობაში ქმნიან რა, პერიოდულად განმეორებად სივრცულ სტრუქტურებს. ასეთი სტრუქტურების თვალსაჩინო წარმოდგენისათვის იყენებენ სივრცულ კრისტალურ მესერებს, რომელთა კვანძებში ნივთიერების ატომების ან მოლეკულების ცენტრებია მოთავსებული. უფრო ხშირად კრისტალური მესერები აგებულია მოცემული ნივთიერების მოლეკულის შემადგენლობაში შემავალი ატომის იონებისგან (დადაებითი და უარყოფითი მუხტიანი ატომენისგან). მაგალითად, სუფრის მარილის მესერი შეიცავს \(Na^{+}\) და \(Cl^{-}\), იონებს, რომლებიც წყვილწყვილად არ არიან დაკავშირებული \(NaCl\) მოლეკულაში (ნახ.1). ასეთ კრისტალებს იონურს უწოდებენ.

ნახ. 1.
სუფრის მარილის კრისტარული მესერი
ყოველ სივრცულ მესერში შეიძლება გამოიყოს მინიმალური ზომის სტრუქტურული ელემენტი, რომელსაც ელემენტარული უჯრედი ეწოდება. მთელი კრისტალური მესერი შეიძლება აიგოს ელემენტარული უჯრედის პარალელური გადატანით სხვადასხვა მიმართულებით.
თეორიულად ნაჩვენებია, რომ სულ შეიძლება არსებობდეს 230 განსხვავებული კრისტალური სტრუქტურა. მათი უმრავლესობა (მაგრამ ყველა არა) ნაპოვნია ბუნებაში ან შექმნილია ხელოვნურად.
მეტალების კრისტალურ მესრებს ხშირად ექვსკუთხა პრიზმის (ცინკი, მაგნიუმი), წახნაგით ცენტრირებული (ოქრო) ან მოცულობით ცენტრირებული (რკინა) კუბის ფორმა აქვთ.
კრისტალური სხეულები შეიძლება იყვნენ მონოკრისტალურები და პოლიკრისტალურები. პოლიკრისტალური სხეულები შედგებიან ერთმანეთთან შეზრდილი, ქაოტურად ორიენტირებული მრავალი პატარა კრისტალისგან, რომლებსაც კრისტალიდებს უწოდებენ. დიდი მონო კრისტალები იშვიათია ბუნებასა და ტექნიკაში. უფრო ხშირად, მყარი სხეულის კრისტაკები, მათ შორის ისინიც, რომლებიც ხელოვნურადაა მიღებული, პოლიკრისტალებს წარმოადგენს.

მონოკრისტალებისგან განსხვავებით, პოლიკრისტალური სხეულები იზოტროპულებია, ე.ი. მათი თვისებები ყველა მიმარტულებით ერთნაირია. მყარი სხეულების პოლიკრისტალური აგებულებაშეიძლება მიკროსკოპოს საშuალებით დავინახoთ, ხანდახან ის შეუიარაღებელი თვალითაც ჩანს.
ბევრი ნივთიერება შეიძლება არსებობდეს განსხვავებული ფიზიკური თვისებების მქონე, მრავალი კრისტალური მოდიფიკაციის სახით (ფაზით). ამ მოვლენაs პოლიმორფიზმს უწოდებენ. ერთი მოდიფიკაციიდან მეორეზე გადასვლას პოლიმორფულ გადასვლას უწოდებენ. პოლიმორფული გადასცლის საინტერესო და მნიშვნელოვანი მაგალითს გრაფიტის ალმასად გარდაქმნა წარმოადგენს. ეს გადასვლა ხელოვნური წარმოებისას 60-100 ათასი ატმოსფერო წნევისა და 1500-2000К ტემპერატურის პირობებში ხორციელდება.
მონოკრისტალებისა და პოლიკრისტალების კრისტალური მესერის სტრუქტურა ექსპერიმენტულად შეისწავლება რენდგენული გამოსხივების დიფრაქციის გამოყენებით.
ნახ, 2-ზე მარტივი კრისტალური მესერების მაგალითებია. უნდა გვახსოვდეს რომ ნაწილაკები კრისტალებში მჭიდროდაა ჩამაგრებული, ისე რომ მათ ცენტრებს შორის მანძილები დაახლოებით ნაწილაკების ზომების ტოლია. წარმოდგენილ კრისტალურ მესერებში მითითებილია მხოლოდ ნაწილაკების ცენტრების მდებარეობები.

ნახ. 2.
უბრალო კრისტალური მესრები: 1 – მარტივი კუბური მესერი; 2 - წახნაგით ცენტრირებული კუბური მესერი; 3 - მოცულობით ცენტრირებული კუბური მესერი; 4 – ჰექსაგონალური მესერი
უბრალო კუბურ მესერში ნაწილაკები განლაგებულია კუბის წვეროებში. წახნაგით ცენტრირებულ მესერში არა მარტო კუბის წვეროებში, არამედ ყოველი წახნაგის ცენტრშიც. ნახ. 1-ზე სუფრის მარილის მესერი შედგება ერთმანეთში ჩაწყობილი ორი, \(Na^{+}\) და \(Cl^{-}\), წახნაგით ცენტრირებული მესერისაგან. მოცულობით ცენტრირებულ კუბურ მესერში დამატებითი ნაწილაკი იმყოფება ყოველი ელემენტარული კუბური უჯრედის ცენტრში.
მეტალების კრისტლურ სტრუქტურას მნიშვნელოვანი თვისება აქვს. მეტალის კრისტალური მესერის წარმომქმნელი დადებითად დამუხტული იონები წონასწორობის მდებარეობაში “თავისუფალი ელექტრონების აირის” ურთიერთქმედებით არიან ჩამაგრებული. ელექტრინული აირი წარმოიქმნება თითოეული ატომის ერთი ან რამოდენიმე ელექტრონის ხარჯზე. თავისუფალ ელექტრონებს შეუძლიათ ხეტიალი კრისტალის მთელ მოცულობაში.

ნახ. 3.
მეტალირი კრისტალის სტრუქტურა
{loadnavigation}
თხევად მდგომარეობაში მყოფი ნივთიერების მოლეკულები თითქმის მიჯრითაა ერთმანეთზე მიწყობილი. მყარი კრისტალური სხეულებისგან განსხვავებით, სადაც მოლეკულები კრისტალის მთელ მოცულობაში მოწესრიგებულ სტრუქტურებს ქმნიან და სითბური რხევის შესრულება მხოლოდ ფიქსირებული ცენტრების მახლობლად შეუძლიათ, სითხის მოლეკულებს დიდი თავისუფლება აქვთ. სითხის ყოველი მოლეკულა, ისევე როგორც მყარ სხეულში, ყველა მხრიდან „მომწყვდეულია“ მეზობელი მოლეკულებით და სითბურ რხევას ასრულებენ გარკვეული წონასწორობის მდებარეობის მახლობლობაში. მაგრამ, დროდადრო ნებისმიერ მოლეკულას შეუძლია გადაადგილდეს მეზობელ ვაკანტურ (ცარიელ) ადგილზე. სითხეებში ასეთი გადახტომები საკმაოდ ხშირად ხდება: ამიტომ მოლეკულები, კრისტალებისგან განსხვავებით, არა რიან მიბმული გარკვეულ ცენტრებთან, და შეუძლიათ მოძრაობა სითხის მთელ მოცულობაში. ამით აიხსნება სითხეების დენადობა. ახლომდებარე მოლეკულების ძლიერი ზემოქმედების გამო, მათ შეუძლიათ რამოდენი მოლეკულისგან შემდგარი, ლოკალური, არამდგრადი მოწესრიგებული ჯგუფების შექმნა. ამ მოვლენას ახლო წესრიგს უწოდებენ (ნახ. 1).

ნახ. 1.
სითხეების ახლო წესრიგისა და კრისტალების შორი წესრიგის მაგალითი: 1 -წყალი; 2 - ყინული.
ნახ. 2-ზე წყლის მაგალითზე ნაჩვენებია აირადი ნივთიერების განსხვავება სითხისგან. წყლის მოლეკულა \(H_{2}O\) შედგება ერთმანეთისადმი 104° გუთხით განლაგებული, ჟანგბადის ერთი ატომისა და წყალბადის ორი ატომისგან. ორთქლის მოლეკულებს შორის საშუალო მანძილი ათეულობით აღემატება წყლის მოლეკულებს შორის საშუალო მანძილს. ნახ. 1 ნახაზისაგან განსხვავებით, სადაც წყლის მოლეკულები ბურთულების სახითაა გამოსახული, ნახ. 2 წყლის მოლეკულის სტრუქტურაზე წარმოდგენას იძლევა.
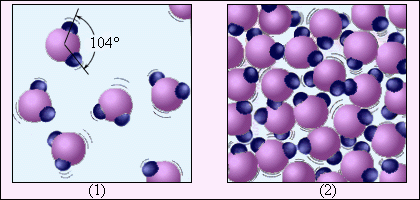
ნახ. 2.
წყლის ორთქლი (1) და წყალი (2). წყილ მოლეკულები დაახლოებით 5·107 -ჯერაა გადიდებული.
მოლეკულების მჭიდრო განლაგების სითხეების კუმშვადობა, ე.ი. წნევის ცვლილებით მოცულობის ცვლილება , ძალიან მცირეა: ათეულ და ასეულჯერ ნაკლებია აირებთან შედარებით. მაგალითად. წყლის მოცულობის 1 % -ით შესაცვლელად წნევა დაახლოებით 200-ჯერ უნდა გაიზარდოს. წნევის ასეთი სიდიდე ატმოსფერულთან შედარებით 2 კმ სიღრმეზე მიიღწევა.
სითხეები, მყარი სხეულიბის მსგავსად, ტემპერატირის ცვლილებისას იცვლიან მოცულობას. ტემპერატურის მცირე ინტერვალებისთვის მოცულობის ფარდობითი ცვლილება \(\frac{\Delta V}{V_{0}}\) ტემპერატირის \(\Delta T\) ცვლილების პროპორციულია:
\(\frac{\Delta V}{V_{0}}=\beta\Delta T.\)
\(\beta\) კოეფიციენტს მოცულობითი გაფართოების კოეფიციენტს უწოდებენ. ეს კოეფიციენტი სითხეებისათვის ათეულობითჯერ აღემატება მყარი სხეილების კოეფიციენტს. წყლისთვის, მაგალითად, 20 °С ტემპერატურისათვის β ≈ 2·10–4 K–1, ფოლადისათვის β ≈ 3,6·10–5 K–1, კვარცის მინისათვის β ≈ 9·10–6 К–1.
წყლის ტემპერატურულ გაფართოებას დედამიწეზე ცხოვრებისთვის საინტერესი და მნიშვნელოვანი ანომალია აქვს. 4 °С -ზე დაბალი ტემპერატურებისთვის წყალი ტემპერატურის შემცირებისას ფართოვდება (β < 0). წყალს მაქსიმალური სიმკვრივე ρ = 103 кг/м3 , 4 °С ტემპერატურაზე აქვს.
გაყინვისას წყალი ფართოვდება, ამიტომ წყალსატევის გაყინვისას ყინული ზედაპირზე ცურავს. წყლის გაყუნვის ტემპერატურა 0 °С-ია. წყლის უფრო მკვრივ ფენებში, წყალსატევების ფსკერზე, წყლის ტემპერატურა 4 °С-რიგისაა. ამის გამო სიცოცხლეს შეუძლია არსებობა ისეთ წყალსატევებში, რომლებიც მთლიანად არ იყინება.
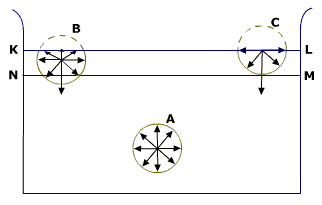
სითხეების განსაკუთრებით საინტერესო თვოსებას თავისუფალი ზედაპირის არსებობა წარმოადგენს. სითხეები, აირებისაგან განსხვავებით, არ ავსებენ ჭურჭელს რომლებშიც არიან ჩასხმული. სითხესა და აირს (ან ორთქლს) შორის წარმოიქმნება საზღვარი, რომელიც სითხის დანარჩენ მასასთან შედარებით განსაკუთრებულ მდგომარეობაში იმყოფება. ამ საზღვრის მიმდებარე ფენის სითხის მოლეკულები, უფრო ღრმა ფენებში მყოფი მოლეკულებისაგან განსხვავებით, იგივე სითხის მოლეკულებით ყველა მხიდან არაა გარშემორტყმული. სითხის შიგნით ერთ მოლეკულაზე მეზობელი მოლეკულების მხრიდან მომქმედი მოლეკულური ურთიერთქმედების ძალები საშუალოდ ურთიერთკომპენსირებულია. სასაზღრო ფენაში მყოფი ყოველი მოლეკულა სითხეში მყოფი მოლეკულების მიერ მიიზიდება (სითხის ამ მოლეკულაზე აირის (ამ ორთქლის) მხრიდან მომქმედი ძალები შეიძლება უგულვებელვყოთ). შედეგად მიიღება რაღაც ტოლქმედი ძალა, რომელიც სითხის შიგნითაა მიმართული. ძედაპირული მოლეკულები მოლეკულათშორისი მიზიდულობის ძალების მოქმედებით გადაადგილდებიან სითხის სიღრმეში. მაგრამ, ყველა მოლეკულა, მათ შორის სასაზრვრო ფენის მოლეკულებიც, უნდა იმყოფებოდნენ წონასწორობის მდგომარეობაში. ეს წონასწორობა მიიღწება სასაზღვრო ფენის მოლეკულებსა და სითხის სიღრმეში მათ უახლოეს მეზობლებს შორის მანძლილის შემცირებით.როგორც ნახ. 2-დან ჩანს, მოლეკულებს შორის მანძილის შემცირებისას აღიძვრება განზიდვის ძალები. თუ სითხის შოგნით მოლეკულებს შორის საშუალო მანძილი r0 ტოლია. მაშინ ზედაპირული ფენის მოლეკულები უფრო მჭიდროდაა განლაგებული. ამიტომაც მათ პოტენციური ენერგიის დამატებითი მარაგი აქვთ სითხეში მდებარე მოლეკულებთან შედარებით (იხ. ნახ. 2). უნდა გვახსოვდეს, რომ სითხეების ძნელად კუმშვადობის გამო უფრო მჭიდროდ განლაგებული ზედაპირული მოლეკულების გამო სითხის მოცულობის რაიმე შესამჩნევ ცვლილებას ადგილი არ ქავს. თუ მოლეკულა ზედაპირიდან სიღრმისაკეს ინაცვლებს, მოლეკულათა შორისი ურთიერთქმედების ძალები ასრულებენ დადებით მუშაობას. და პირიქით, სიღრმიდან რამოდენიმე მოლეკულის ზედაპირზე ამოსაყვანად (ე.ი. რომ გავზარდოთ ზედაპირის ფართობი) გარე ძალებმა უნდა შეასრულოს ზედაპირის ფართობის ΔS ცვლილების პროპორციული დადებითი მუშაობა ΔAგარე :
ΔAგარე = σΔS.
პროპორციულობის σ კოეფიციენტს ზედაპირული დაჭიმულობის კოეფიციენტს უწოდებენ (σ > 0). ამგვარად, ზედაპირული დაჭიმულობის კოეფიციენტი იმ მუშაობის ტოლია, რომელის საჭიროა მუდმივი ტემპერატურის პირობებში ზედაპირის ფართობის ერთი ერთეულით გაზრდისათვის.
სი სისტემაში ზედაპირული დაჭიმულობის კოეფიციენტი იზომება ჯოული/მ2 ან ნ/მ2-ით.
აქედან გამომდინარე. ზედაპირული ფენის მოლეკულებს სითხის შიგნით მყოფ მოლეკულებთან შედარებით ჭარბი პოტენციური ენერგია აქვს. სითხის ზედაპირის პოტენციური ენერგია ზედაპირის ფართობის პროპორციულია:
Eр = Aგარე = σS.
მექანიკიდან ცნობილა, რომ სისტემოს წონასწორულ მდგომარეობას პოტენციური ენერგიის მინიმალური მნიშვნელობა შეესაბამება. აქედან გამომდინარე, სითხის თავისუფალი ზედაპირი ცდილობს შეამციროს თავისი ფართობი. ამ მიზეზით სითხის თავისუფალი წვეთი სფეროსებურ ფორმას ღებულობს. სითხე ისე იქცევა, თითქოს მისი ზედაპირის მხების გასწვრივ მოქმედებს ამ ზედაპირის მომჭიმავი (შემკუმშავი, შემამცირებელი) ძალები. ამ ძალებს ზედაპირული დაჭიმულობის ძალები ეწოდება.

ზედაპირული ძალების არსებობა სითხის ზედაპირს დრეკადი გადაჭიმული აპკის მაგვარს ხდის, იმ განსხვავებით, რომ აპკის დრეკადი ძალები დამოკიდებულია მისი ზედაპირის ფართობზე (ე.ი. თუ როგოორაა აპკი დეფორმირებული), ხოლო ზედაპირული დაჭიმულობის ძალები სითხის ზედაპირის ფართობზე არ არიან დამოკიდებული.
ზოგიერთ სითხეს, მაგალითად, საპნიან წყალს, ახასიათებს თხელი აპკის შექმნის უნარი. ყველასთვის კარგად ცნობილი საპნის ბუშტებს სფერული ფორმა აქვთ - ამაშიც ზედაპირული დაჭიმულობის ძალების მოქმედება ვლინდება. თუ საპნის ხსნარში ჩაუშვებთ მავთულის ჩარჩოს. რომლის ერთ მხარეს მოძრაობა შეუძლია, იგი სითხის აპკით დაიფარება. (ნახ. 3).
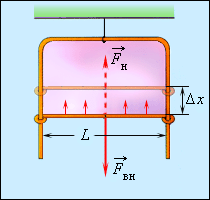
ნახ. 3.
ჩარჩოს მოძრავი მხაერე წონასწორობაშია გარე \(\vec{F_{g}}\) ძალისა და ზედაპირული დაჭიმულობის \(\vec{F_{d}}\) ძალების ტოლქმედის ზემოქმედების შედეგად.
ზედაპირული დაჭიმულობის ძალები ცდილობენ შეამცირონ აპკის ზედაპირი. ჩარჩოს მოძრავი მხარის წონასწორობისთვის მას უნდა მოვდოთ გარე ძალა \(\vec{F_{g}}=-\vec{F_{d}}\) თუ \(\vec{F_{g}}\) ძალის მოქმედებით ეს გვერდი გადაადგილდა \(\Delta x\)-თი, მაშინ შესრულდა მიშაობა \(\Delta A_{g}=F_{g}\Delta x=\Delta E_{p}=\sigma \Delta S\), სადაც \(\Delta S=2L\Delta x\) – საპნის აპკის ორივე მხარის ზედაპირი ფართობის ნაზრდია. რადგანაც \(\vec{F_{g}}\) და \(\vec{F_{d}}\)ძალების მოდულები ერთნაირია. შეიძლება ჩაიწეროს:
\(F_{d}\Delta x=\sigma2L\Delta x\) ან \(\sigma=\frac{F_{d}}{2L}.\)
ამგვარად. ზედაპირული დაჭიმულობის კოეფიციენტი σ შეიძლება განისაზღვროს როგორც, ზედაპირის შემომსაზღვრელი წრფის ერთეულ სიგრძეზე მომქმედი დაჭიმულობის ძალის მოდული.
ძედაპირული დაჭიმულობის ძალების მოქმედების გამო სითხის წვეთებში და საპნის ბუშტების შიგნით წარმოიქმნება ჭარბი წნევა \(\Delta p\). თუ წარმოვიდგენთ, რომ გავჭერით \(R\) რადიუსიანი სფერული წვეთი ორ ტოლ ნაწილად, თითოეული მათგანი გაჭრის \(2\pi R\) ტოლი სიგრძის საზღვარზე მოდებული ზედაპირული დაჭიმულობის ძალებისა და \(\pi R^{2}\) ფართობის მქონე კვეთაზე მომქმედი ჭარბი წნევის ძალების მოქმედების შედეგად უნდა იმყოფებოდეს წონასწორობაში (ნახ.4). წონასწორობის პირობები ასე ჩაიწერება:
\(\sigma2\pi R=\Delta p\pi R^{2}\)
აქედან გამომდინარე, წვეთის შიგნით ჭარბი წნევა ტოლია
\(\Delta p=\frac{2\sigma}{R}\)(სითხის წვეთი)

ნახ. 4.
სითხის სფერული წვეთის კვეთა
ჭარბი წნევა საპნის ბუშტის შიგნით ორჯერ მეტია, რადგან აპკს ორი ზედაპირი აქვს:
\(\Delta p=\frac{4\sigma}{R}\)(საპნის ბუშტი)
სითხის, მყარი სხეულისა და აირის საზღვრის მახლობლად სითხის თავისუფალი ზედაპირის ფორმა დამოკიდებულია სითხის მოლეკულების მყარი სხეულის მოლეკულებთან ურთიერთქმედების ძალებზე (აირის (ან ორთქლის) მოლეკულებთან ურთიერთქმედება შეიძლება უგულვებელყოთ). თუ ეს ძალები მეტია სითხის მოლეკულებს შორის ურთიერთქმედების ძალებზე, მაშინ სითხე ასველებს მყარი სხეულის ზედაპირს. ასეთ შემთხვევაში სითხე უახლოვდება მყარი სხეულის ზედაპირს გარკვეული θ მახვილი კუთხით, რომელიც ახასიათებს სითხე-მყარი სხეულის მოცემულ წყვილს. θ კუთხეს კიდის კუთხე ეწოდება. თუ სითხის მოლეკულებს შორის ურთიერთქმედების ძალები სითხის მოლეკულების მყარი სხეულის მოლეკულებთან ურთიერთქმედების ძალებზე მეტია, მაშინ კიდის კუთხე θ ბლაგვია (ნახ. 5).ამ შემთხვევაში ამბობენ, რომ სითხე არ ასველებს მყარი სხეულის ზედაპირს. სრული დასველებისას θ = 0, სრული არდასველებისას θ = 180°.
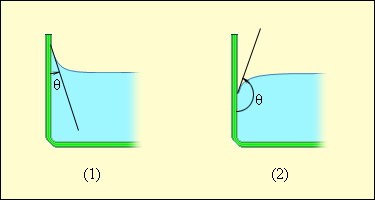
ნახ. 5.
დამასველებელი (1) და არადამასველებელი (2) სითხეების მრუდე კუთხეები.
კაპილარული მოვლენა ეწოდება მცირე დიამეტრის მილებში - კაპილარებში, სითხის აწევას ან დაშვებას. დამასველემელი სითხეები კაპოლარებში ზევით იწევენ, არადამასველებლები კი ქვევით ეშვებიან.
ნახ. 6-ზე გამოსახულია ქვედა ბოლოთი ρ სიმკვრივის სითხეში დამასველებელ სითხეში ჩაშვებული, r რაღაც რადიუსის კაპილარული მილი. კაპილარის ზედა ბოლო ღიაა. კაპილარში სითხის აწევა მანამდე გრძელდება, სანამ კაპილარში სითხის სვეტზე მომქმედი Fსიმძ სიმძიმის ძალა მოდულით არ გაუტოლდება ჯამურ დაჭიმვის Fდაჭ ძალას, რომელიც მოქმედებს კაპილარის კედელთან შეხების საზღვრის გასწვრივ: Fსიმძ = Fდაჭ, სადაც Fსიმძ = mg = ρhπr2g, Fდაჭ = σ2πr cos θ.
აქედან გამომდინარე:
\(h=\frac{2\sigma\cos\theta}{\rho gr}\)
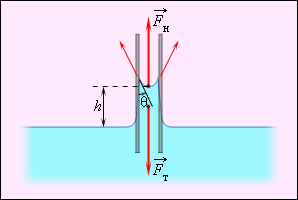
ნახ. 6.
კაპილარში დამასველებელი სითხის ასვლა
სრული დასველებისას θ = 0, cos θ = 1. ამ შემთხვევაში
\(h=\frac{2\sigma}{\rho gr}.\)
სრული არადასველებისას θ = 180°, cos θ = –1 და. ე.ი. h < 0. კაპილარში არადამასველებელი სითხის დონე დაბლა იწევს იმ ჭურჭელში სითხის დონესთან შედარებით, რომელშიაც ჩაშვებულია კაპილარი.
წყალი პრაქტიკულად მთლიანად ასველებს მინის სუფთა ზედაპირს. ვერცხლისწყალი, პირიქით სულ არ ასველებს მინის ზედაპირს. ამიტომ ვერცხლისწყლის დონე მინის კაპილარში უფრო დაბლა ეშვება, ვიდრე ჭურჭელში, რომელშიც კაპილარია ჩაშვებული.
{loadnavigation}
ნებისმიერ ნივთიერებას გარკვეულ პირობებში შეუძლია იმყოფებოდეს სხვადასხვა აგრეგატულ მდგომარეობაში - მყარ, თხევად ან აირად. ერთი მდგომარეობიდან მეორეში გადასვლას ფაზურ გადასვლას უწოდებენ. აორთქლება და კონდენსაცია ფაზური გადასვლის მაგალითებს წარმოადგენენ.
ყველა რეალურ აირს (ჟანგბადი, აზოტი, წყალბადი და სხვა) გარკვეულ პირობებში შეუძლია სითხედ გადაქცევა. მაგრამ ეს გადაქცევა შეიძლება ხდებოდეს მხოლოდ გარკვეული, ე.წ. კრიტიკულ Tkr ტემპერატურაზე დაბალ ტემპერატურაზე. მაგალითად, წყლისათვის კრიტიკული ტემპერატურა ტოლია 647,3 K, აზოტისათვის -126 K, ჟანგბადისათვის- 154,3 K. ოთახის ტემპერატურაზე (≈ 300 K) წყალი შიუძლება იყოს თხევად და აირად მდგომარეობაში, აზოტი და ჟანგბადი კი მხოლოდ აირადი სახით.
აორთქლება ეწოდება თხევადი მდგომარეობიდან აირად მდგომარეობაში ფაზურ გადასვლას. მოლეკულურ-კინეტიკური თეორიის თვალსაზრისით, აორთქლება არის პროცესი, რომლის დროსაც სითხის ზედაპირიდან ამოფრიმდება განსაკუთრებით დიდი სიჩქარის მქონე მოლეკულები, რომელთა კინეტიკური ენერგია მეტია მათი სხვა მოლეკულებთან კავშირის ენერგიაზე. ეს იწვევს დარჩენილი მოლეკულების საშუალო კინეტუკური ენერგიის შემცირებას, ე.ი. სითხის გაციებას (თუ არ არსებობს გარემომცველი სხეულებიდან სითბოს გადაცემა).
კონდესაცია - აორთქლების შებრუნებული პრიცესია. კონდენსაციისას ორთქლის მოლეკულები სითხეში ბრუნდებიან.
დახუფულ ჭურჭელში სითხე და მისი ორთქლი შეიძლება იმყოფებოდნენ დინამიკური წონასწორობის მდგომარეობაში, როცა სითხიდან ამოფრენილი მოლეკულების რაოდენობა ტოლია ორთქლიდან სითხეში დაბრუნებული მოლეკულების რაოდენობისა, ე.ი. როცა აორთქლების და კინდენსაციის პროცესების სიჩქარეები ერთნაირია. ასეთ სისტემას ორფაზიანსუწოდებენ. სითხესთან წონასწორობაში მყოფ ორთქლს გაჯერებულს უწოდებენ.
სითხის ზედაპირის ფართობის ერთეულიდან ერთ წამში ამოფრენილი მოლეკულების რიცხვი სითხის ტემპერაურაზეა დამოკიდებული. ორთქლიდან სითხეში დაბრუნებული მოლეკულების რიცხვი დამოკიდებულია ორთლის მოლეკულების კონცენტრაციაზე და მათი სითბური მოძრაობის საშუალო სიჩქარეზე, რაც ორთქლის ტემპერატურით განისაზღვრება. აქდან გამოდის, რომ მოცემული ნივთიერებისთვის სითხისა და მისი ორთქლის წონასწორობისას, ორთქლის მოლეკულების კონცენტრაცია განისაზღვრება მათი წონასწორობის ტემპერატურით. ტემპერატურის გაზრდისას აორთქლებისა და კონდენსაციის პროცესებს შორის დინამიკური წონასწორობის დამყარება ორთქლის მოლეკულების უფრო მაღალი კონცენტრაციის დროს ხდება. რადგანაც აირის (ორთქლის) წნევა მისი კონცენტრაციითა და ტემპერატურით განისაზღვრება, შეიძლება დავასკვნათ: მოცემული ნივთიერების გაჯერებული ორთქლის წნევა p0 დამოკიდებულია მხოლოს მის კონცენტრაციაზე და არა არის დამოკიდებული მოცულობაზე. ამიტომ რეალური აირების იზოთერმებს (\(p\), \(V\)) სიბრტყეზე გააჩნიათ ჰორიზონტული მონაკვეთები, რომლებიც ორფაზიან სისტემებს შეესაბამება (ნახ. 1).

ნახ. 1.
რეალური აირი იზოთერმები. I არე – სითხე, II არე – ორფაზა სისტემა «სითხე+გაჯერებული ორთქლი», III არე – ნივთიერება აირადი სახით. K – კრიტიკული წერტილი.
ტემპერატურის გაზრდისას გაჯერებული ორთქლის წნევა და სიმკვრივე იზრდება, ხოლო სითხის სიმკვრივე სითფური გაფარფოების ხარჯზე კლებულობს. მოცემული ნივთიერების კრიტიკული Tkr ტემპერატურისას სითხისა და აირის სიმკვრივეები თანაბრდება. როცა T > Tkr, სითხისა და მის გაჯერებულ ორთქლს შორის ფიზიკური განსხვავება ქრება.
თუ გაუჯერებელ ორთქლს იზოთერმულად შევკუმშავთ, როცა T < Tkr, მისი წნევა გაიზრდება სანამ გაჯერებული ორთქლის წნევის ტოლი არ გახდება. მოცულობის შემდგომი შემცირებისას, ჭურჭლის ფსკერზე წარმოიქმნება სითხე და დამყარდება დინამიკური წონასწორობა სითხესა და მის ორთქლს შორის. მოცულობის კიდევ უფრო შემცირებით ორთქლის დიდი ნაწილი კონდენსირდება, მისი წნევა კი დარჩება უცვლელი (იზოთერმის ჰორიზონტული უბანი). როცა ორთქლი მთლიანად სითხედ გადაიქცევა, მოცულობის შემდგომი შემცირებისას წნევა მკვეთრად მოიმატებს, სითხის ცუდად კუმშვადიბის გამო.
აირადი მდგომარეიბიდამ თხევადში გადასვლა ორფაზა უბნის გავლის გარეშეცაა შესაძლებელი. ამისათვის პროცესი უნდა მიმდინარეობდეს კრიტიკული K წერტილის გვერდის ავლით. ერთი ასეთი შესაძლო პროცესი ნახ. 1-ზეა მოცემული \(ABC\) ტეხილის სახით.
გაჯერებული ორთქლის წნევა \(p_{0}\) ტემპერატურის \(T\) ზრდით ძალიან სწრაფად იზრდება. \(p_{0}(T)\) დამოკიდებულების მიღება იდეალური აირის კანონებიდან შეიძლება. მოლეკულების მუდმივი კონცენტრაციის პირობებში აირის წნევა ტემპერატურის პირდაპირპროპორციულია. გაჯერებულ ორთქლში ტემპერატურის გაზრდისას იზრდება არა მხოლოდ მოლეკულების საშუალო კინეტიკური ენერგია, არამედ მათი კონცენტრაციაც. ამიტომ გაჯერაბული ორთქლის წნევა ტემპერატურის გაზრდისას უფრო სწრაფად იზრდება, ვიდრე იდეალური აირის წნევა მოლეკულების მუდმივი კონცენტრაციისას.
აორთქლება შეიძლება ხდებოდეს არა მხოლოს ზედაპირიდან, არამედ სითხის მოცულობაშიც. სითხეში ყოველთვის იმყოფება აირის მცირე ბუშტუკები. თუ გაჯერებული ორთქლის წნევა ტოლია ან მეტია გარემომცველი წნევისა (ე.ი. აირის ბუშტუკებში წნევის), სითხე აორთქლდება ბუშტუკეის შიგნით. ორთქლით ავსებული ბუშტუკები ფართოვდება და ზევით ამოტივტივდება. ამ პროცესს დუღილი ეწოდება.


ამგვარად, სითხის დუღილი იწყება ისეთი ტემპერატურის დროს, როდესაც გაჯერებული ორთქლის წნევა გარემოს წნევის ტოლი ხდება.
კერძოდ, ნორმალური ატმოსფერული წნევისას წყალი დუღს 100 °С ტემპერატურაზე. ეს ნიშნავს, რომ ასეთ ტემპერატურაზე გაჯერებული ორთქლის წნევა 1 ატმ-ს ტოლია. მთაში ასვლისას ატმოსფერული წნევა კლებულობს და ამიტოს წყლის დუღილის ტემპერატურაც კლებულობს (დაახლოებით 1 °С -ით ყოველი 300 მ-ით ასვლისას). 7კმ სიმაღლეზე წნევა დაახლოებით 0,4 ატმოსფეროა, და დუღილის ტემპერატურა მცირდება 70 °С-მდე.
ჰერმეტულად დახუფულ ჭურჭელში სითხეს დუღილი არ შეუძლია, რადგან ტემპერატურის ნებისმიერი მნიშვნელობისათვის მყარდება წონასწორობა სითხესა და მის გაჯერებულ ორთქლს შორის. \(p_{0}(T)\) წონასწორობის მრუდის საშუალებით შესაძლებელია დუღილის ტემპერატურის დადგენა სხვადსხვა წნევის შემთხვევაში.
ნახ. 1 -ზე გამოსახული რეალური აირის იზოთერმები აორთქლებისა და კონდენსაციის პროცესებს აღწერენ, ე.ი. ნივთიერების აირად და თხევად ფაზებს შორის ფაზურ გადასვლებს. სინამდვილეში ეს სურათი არასულია, რადგან აირადი და თხევადი მდგომარეობიდან ნებისმიერი ნივთიერება შეიძლება გადავიდეს მყარ მდგომარეობაში. მოცემული \(T\)ტემპერატურისას ერთიდაიგივე ნივთიერების ორ ფაზას შორის თერმოდინამიკური წონასწორობა შესაძლებელია მხოლოდ სისტემაში წნევის გარკვეული მნიშვნელობისთვის. წონასწორობის წნევის ტემპერატურაზე დამოკიდებულებას ფაზური წონასწორობის მრუდი ეწოდება. მაგალითად გამოდგება \(p_{0}(T)\) გაჯერებული ორთქლის და სითხის წონასწორობის მრუდი. თუ სხვადასხვა ფაზას შორის წონასწორობის მრუდებს ავაგებთ \((p,T)\) სიბრტყეზე, მაშინ ისინი ამ სიბრტყეს ყოფენ ცალკეულ არეებად, რომლებშიც ნივთიერება იმყოფება ერთგავაროვან აგრეგატულ მდგომარეობაში - მყარ, თხევად ან აირად (ნახ. 2.). \((p,T)\) სიბრტყეზე გამოსახულ წონასწორობის მრუდებს ფაზურ დიაგრამებს უწოდებენ.

ნახ. 2.
ტიპური ფაზური დიაგრამა. \(K\) – კრიტიკული წერტილი, \(T\) – სამმაგი წერტილი. I არე – მყარი სხეული, II არე – სითხე, III არე – აირი.
\(OT\) მრუდი მყარ და აირად ფაზებს შორის წონასწორობას შეესაბამება და სუბლიმაციის მრუდი ეწოდება. \(TK\) მრუდი წონასწორობაა სითხესა და ორთქლს შოროს და აორთქლების მრუდი ეწოდება. იგი კრიტიკულ \(K\) წერტილში წყდება. \(TM\) მრუდი შეესამაბება მყარ სხეულსა და თხევადს შორის წონასწორობას და დნობის მრუდი ეწოდება.
წონასწორობის მრუდები \(T\) წერტილში იყრიან თავს, სადაც სამივე ფაზა წონასწორობაში შეიძლება თანამყოფობდეს. ამ წერტილს სამმაგი წერტილიეწოდება.
მრავალი ნივთიერებისათვის pтр სამმაგ წერტილში 1 ატმ ≈ 105 პა-ზე ნაკლებია. ასეთი ნივთიერებები ატმოსფერულ წნევაზე გაცხელებისას დნებიან. მაგალითად, წყლის სამმაგი წერტილის კოორდინატებია Tтр = 273,16 К, pтр = 6,02·102 პა და გამოიყენება საყრდენ წერტილად კელვინის აბსოლუტური ტემპერატურული შკალის კალიბრირებისათვის (დაყალიბებისათვის). მაგრამ არსებობენ ისეთი ნივთიერებებიც, რომელთა pтр 1 ატმ-ზე მეტია. მაგალითად ნახშირორჟანგისათვის (CO2) წნევა pтр = 5,11 ატმ-ია და ტემპერატურა კი Tтр = 216,5 К. ამიტომ ატმოსფერულ წნევაზე ნახშირორჟანგი შეიძლება არსებობდეს მხოლოა დაბალ ტემპერატურაზე, თხევადში p = 1 ატმ იგი საერთოდ არ არსებობს. ატმოსფერულ წნევაზე მყარ მდგომარეობაში თავის ორთქლთან წონასწორობაში ნახშირორჟანგი იმყოფება 173 К ან –80 °С ტემპერატურაზე. ეს არის ფართო გამოყენებაში მყოფი „მშრალი ყინული“ რომელიც არასოდეს დნება, მხოლოდ ორთქლდება (სუბლიმირდება).
