{loadnavigation}

ძირითად მოდელს, რომელიც მოლეკულურ-კინეტიკურ  თეორიაში განიხილება იდეალური აირის მოდელი წარმოადგენს.  კინეტიკურ მოდელში იდეალური აირის მოლეკულები განიხილება, როგორც მყოფი იდეალურად დრეკადი ბურთულები, რომლებიც ერთმანეთთან და კედლებთან ურთიერთქმედებენ მხოლოდ დრეკადი დაჯახებებით. ყველა მოლეკულის ჯამური მოცულობა იმ ჭურჭლის მოცულობასთან შედარებით, რომელშიაც აირია მოთავსებული, უმნიშვნელოა. იდეალური აირის მოდელი საკმაოდ კარგად აღწერს რეალური აირების ყოფაქცევას წნევისა და ტემტერატურების საკმაოდ დიდ დიაპაზონში. მოლეკულარულ-კინეტიკური თეორიის ამოცანა იმაში მდგომარეობს, რომ დადგინდეს კავშირი მიკროსკოპულ (მოლეკულების მასა, სიჩქარე, კინეტირური ენერგია) და მაკროსკოპულ პარამეტრებს (წნევა, მოცულობა და ტემპერატურა) შორის.

მოლეკულებსა და მოლეკულასა და კედლებს შორის ყოველი შეჯახების შედაგად მოლეკულების სიჩქარეები შეიძლება შეიცვალის სიდიდითაც და მიმართულებითაც; დაჯაებებს შორის დროის ინტერვალებში მოლეკულები მოძრაობენ წრფივად და თანაბრად. იდეალური აირის მოდელში იგულისხმება, რომ ყველა დაჯახება დრეკადი დაჯახებების კანონებით ხდება, ე.ი. ემორჩილება ნიუტონის კანონებს.

იდეალური აირის მოდელის გამოყენებით გამოვითვალით აირის წნევა ჭურჭლის კედლებზე. კედლებთან მოლეკულების ურთიერთქმედების პროცესში მათ შორის აღიძვრება ძალები, რომლების ნიუტონის მესამე კანონს ემორჩილებიან. ამის შედეგად კედლისადმი მოლეკულის  მართობული სიჩქარის \(v_{x}\) გეგმილი იცვლის ნიშანს, ხოლო სიჩქარის \(v_{y}\) გეგმილი, რომელიც კედლის პარალელურია, უცვლელი რჩება.

ნახ. 3.2.1.

მოლეკულების  დრეკადი დაჯახება კედლთან.

 

ამიტომ მოლეკულის იმპულსის ცვლილება ტოლი იქნება  \(2m_{0}v_{x}\), სადაც \(m_{0}\) – მოლეკულის მასაა.

კედელზე გამოვყოთ რაღაც ფართობი \(S\)  (ნახ. 3.2.2).   \(\Delta t\) დროის განმავლობაში ამ ფართობს დაეჯახება ყველა მოლეკულა, რომლების სიჩქარის \(v_{x}\) გეგმილი კედლისკენაა მიმართული და იმყოფებიან  \(S\) ფართობისა და \(v_{x}\Delta t\) სიმაღლის მქონე ცილინდრში.

ნახ. 2.

\(S\) ფართობზე მოლეკულების დაჯახებების რიცხვის განსაზღვრა.

 

ვთქვათ ჭურჭლის მოცულობის ერთეულში \(n\) მოლეკულაა; მაშინ ცილინდრის მოცულობაში მოლეკულების რიცხვი \(nSv_{x}\Delta t\) ტოლია. მაგრამ მათგან მხოლოდ ნახევარი მოძრაობს კედლის მიმართულებით, დანარჩენები კი საწინააღმგეგო მიმართულებით მოძრაობენ და კედელს არ ეჯახებიან. აქედან გამომდინარე \(S\) ფართობთან დაჯახებების რიცხვი \(\Delta t\) დროში ტოლია \(\frac{1}{2}nSv_{x}\Delta t.\) რადგანაც ყოველი მოლეკულა კედელთან დაჯახებისას იცვლის იმპულსს \(2m_{0}v_{x}\) სიდიდით, \(\Delta t\) დროში \(S\)ფართობთან შეჯახებული ყველა მოლეკულის იმპულსის სრული ცვლილება ტოლია \(nm_{0}v_{x}^{2}S\Delta t.\) მექანიკის კანონების მიხედვით იმპილსიის  ეს ცვლილება ხდება \(F\Delta t\) ძალის იმპულსის მოქმედებით ,სადაც \(F\) – \(S\) ფართობზე კედლის მხრიდან მოლეკულებზე მომქმედი გარკვეული საშუალო ძალაა. მაგრამ ნიუტონის მესამე კანონის მიხედფით მოდულით ტოლი ძალა მოქმედებს კედლის \(S\) ფართობზე მოლეკულების მხრიდანაც. ამიტომ შეიძლება დაიწეროს: 

\(F\Delta t=nm_{0}v_{x}^{2}S\Delta t.\)

თუ განტოლების ორივე მხარეს \(S\Delta t\)-ზე გავყოფთ, მივიღებთ:

\(p=\frac{F}{S}=nm_{0}v_{x}^{2},\)

სადაც \(p\) -ჭურჭლის კედელზე აირის წნევაა.

ამ თანაფარდობის გამოყვანისას იგულისხმებოდა, რომ მოცულობის ერთეულში არსებულ ყველა \(n\) მოლეკულას \(X\) ღერძზე ერთნაირი გეგმილები აქვთ. სინამდვილეში ეს ასე არ არის.

ჭურჭელში, რომელიც მოლეკულების დიდ რიცხვს შეიცავს, აირის მოლეკულების ერთმანეთთან და კედლებთან მრავალჯერადი დაჯახების შედეგად მყარდება მოლეკულების სიჩქარეების  გარკვეული სტატისტიკური განაწილება. ამასთან, მოლეკულების სიჩქარის ვექტორების ყველა მიმართულება თანაბარუფლებიანი (თანაბარალბათური) აღმოჩნდება, სიჩქარის მოდულები და მათი გეგმილები კოორდინატთა ღერძებზე გარკვეულ კანონზომიერებებს ემორჩილებიან. აირის მოლეკულების განაწილებას სიჩქარის მოდულების მიხედვით მაქსველის განაწილება ეწოდება. მაქსველმა 1860 წელს გამოიყვანა აირის მოლეკულების განაწილების კანონი სიჩქარეების მიხედვით, მოლეკულურ-კინეტიკური თეორიის დებულებეზე დაყრდნობით. ნახ. 3-ზე მოლეკულების სიჩქარეების მიხედვით განაწილების ტიპური მრუდებია გამოსახული. აბსცისთა ღერძზე მოლეკულათა სიჩქარეებია გადაზომილი, ხოლო ორდინატთა ღერძზე - მოლეკულების ფარდობითი რიცხვი, რომელთა სიჩქარეები  \(v\)-დან \(v+\Delta v\)-მდე ინტერვალშია მოთავსებული. ეს რიცხვი ტოლია ნახ. 3-ზე გაფერადებული სვეტის ფართობისა.

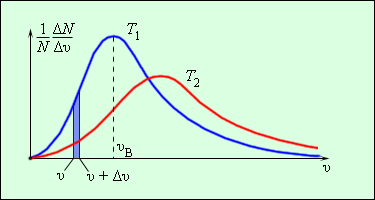
ნახ. 3.

მოლეკულების სიჩქარეების მიხედვით განაწილება. \(T_{2}>T_{1}\).

 

მაქსველის განაწილების დამახასიათებელ პარამეტრს წარმოადგენს განაწილების მრუდის მაქსიმუმის შესაბაბისი უალბათესი სიჩქარე \(v_{a}\)  და საშუალო კვადრატული სიჩქარე \(v_{kv}=\sqrt{\bar{v}^{2}}\) სადაც \(\bar{v}^{2}\), სიჩქარის კვადრატის საშუალი მნიშვნელობაა.  

ტემპერატურის მატებით განაწილების მრუდის მაქსიმუმი დიდი სიჩქარეებისკენ ინაცვლებს, ამსთან  \(v_{a}\) და \(v_{kv}\) იზრდება.

აირის ჭურჭლის კედლებზე წნევის ფორმულის დასაზუსტებლად დავუშვათ, რომ მოცულობის ერთეულში შემავალი ყველა მოლეკულა დანაწილებულია ჯგუფებად, რომლებიც შეიცავენ \(n_{1},\, n_{2},\, n_{3}\) და ა.შ. მოლეკულას \(v_{x1},\, v_{x2},\, v_{x3}\) და ა.შ. სიჩქარის გეგმილებით, შესაბამისად. ამასთან \(\sum_{i}n_{i}=n.\)მოლეკულათა ყოველ ჯგუფს აირის წნევაში შეაქვს თავისი წვლილი \(n_{i}m_{0}v_{xi}^{2}\) . სიჩქარის სხვადასხვა გეგმილების \(v_{xi}\)  მქონე მოლეკულების კედელთან შეჯახების შედეგად იქმნება ჯამური წნევა 

ამ გამოსახულემაში შემავალი ჯამი მოცულობის ერთეულში შემავალი  ყველა \(n\) მოლეკულის სიჩქარის გეგმილების \(v_{x}\) კვადრატების ჯამია.  თუ ამ ჯამს  \(n\)-ზე გავყოფთ, მივიღებთ მოლეკულის სიჩქარის გეგმილების \(v_{x}\) კვადრატების საშუალო მნიშვნელობას \(\bar{v_{x}^{2}}\) -ს, მივიღებთ: 

\(\frac{1}{n}\sum_{i}n_{i}v_{xi}^{2}=\bar{v_{x}^{2}}.\)

ახლა აირის წნევის ფორმულა შეიძლება ჩაიწეროს შემდეგი სახით:

\(p=nm_{0}\bar{v_{x}^{2}}.\)

რადგანაც მოლეკულების სიჩქარის ვექტორების ყველა მიმართულება თანაბარალბათურია, ღერძებზე მათი გეგმილების საშუალო კვადრატული მნიშვნელობებიც ტოლია:

\(\bar{v_{x}^{2}}=\bar{v_{y}^{2}}=\bar{v_{z}^{2}}=\frac{1}{3}\bar{v^{2}}.\)

ეს ბოლო ტოლობა გამომდინარეობს ფორმულიდან: \(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}=v^{2}.\)

აირის საშუალო წნევის ფორმულა ჩაიწერება ასე:

\(p=\bar{p}=\frac{1}{3}nm_{0}\bar{v^{2}}=\frac{2}{3}n\frac{m_{0}\bar{v^{2}}}{2}=\frac{2}{3}n\bar{E_{k}}.\)

ეს განტოლება ამყარებს კავშირს იდეალური აირის წნევას p , მოლეკულის მასას \(m_{0}\), მოლეკულების კონცენტრაცია \(n\), სიჩქარის საშუალო კვადრატულ მნიშვნელობასა \(\bar{v^{2}}\) და მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკურ ენერგიას   \(\bar{E_{k}}\)    შორის.  ამ განტოლებას აირის მოლეკულურ-კინეტიკური თეორიის ძირითად განტოლებას უწოდებენ.

ამგვარად, აირის წნევა ტოლია მოცულობის ერთეულში შემავალი მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკურ ენერგიის  ორი მესამედისა.

აირების მოლეკულურ-კინეტიკური თეორიის ძირითად განტოლებებში შედის მოლეკულების კონცენტრაციის \(n\) ფარდობა მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკურ \(\bar{E_{k}}\) ენერგიასთან.  თუ დავუშვებთ, რომ აირი იმყოფება უცვლელი \(V\) მოცულების ჭურჭელში, მაშინ \(n=\frac{N}{V}=const\) (\(N\)– ჭურჭელში მოლეკულების რიცხვი). ამ შემთხვევაში წნევის ცვლილება \(\Delta p\) პროპორციულია საშუალო კინეტიკური ენერგიის \(\Delta\bar{E_{k}}\) ცვლილების.

ისმის კითხვები: უცვლელი მოცულობის ჭურჭელში ცდით როგორ შეიძლება შეიცვალოს მოლეკულების მოძრაობის საშუალო კინეტიკური ენერგია? რა ფიზიკური სიდიდე უნდა შეიცვალოს, რომ შეიცვალოს საშუალო კინეტიკური ენერგია?  ცდები უჩვენებენ, რომ ასეთი სიდიდე ტემპერატურაა.

ტემპერატურის ცნება მჭიდროდაა დაკავშირებული სითბური წონასწორობის ცნებასთან. ერთმანეთთან შეხებაში მყოფი სხეულებს შეუძლიათ ენერგიის გაცვლა. სითბული კონტაქტისას ერთი სხეულიდან მეორისთვის გადაცემულ ენერგიას სითბოს რაოდენობას უწოდებენ.

სითბური წონასწორობა - სითბურ კონტაქტში მყოფ სხეულთა სისტემის ისეთი მდგომარეობაა, რომლის დროსაც არ ხდება სითბოს გადაცემა ერთი სხეულიდან მეორეზე და სხეულების ყველა მაკროსკოპული მახასიათებელი უცვლელი რჩება. ტემპერატურა - ეს ფიზიკური პარამეტრი, სითბურ წონასწორობაში მყოფი ყველა სხეულისათვის ერთიდაიგივეა. ტემპერატურის ცნების შემოტანა  დაკვირვეეიბიდან გახდა შესაძლებელი და ცნობილია თერმოდინამიკის ნულოვანი კანონის სახელწოდებით.

ტამპერატურის გასაზომად გამოიყენება ფიზიკური ხელსაწყოები - თერმომეტრები - რომლების საშუალებითაც ტემპერეტურის სიდიდეზე მსჯელობენ რომელიმე ფიზიკური პარამეტრის ცვლილების საფუძველზე. თერმომეტრის შესაქმელად აუცილებელია თერმომეტრული ნივთიერების არჩევა (მაგ. ვერცხლისწყალი, სპირტი) და ამ ნივთიერებისთვის დამახასიათებელი თერმომეტრული სიდიდე (მაგ. ვერცხლისწყლის სვეტის ამ  სპირტის სვეტის სიმაღლე). თერმომეტრების სხვადასხვა კონსტრუქციებში ნივთიერებების სხვარასხვა ფიზიკური თვისებები გამოიყენება (მაგ., მყარი სხეულების გრძივი ზომების ცვლილება ან გათბობისას გამტარების ელექტრული წინაღობის ცვლილება).

თერმომეტრები უნდა იყვნენ კალიბრირებული. ამისათვის ისინი შეყავთ სითბურ კონტაქტში ისეთი სხეულებთან, რომელთა ტემპერატურა ითვლება წინასწარ განსაზრვრულად. ყველაზე ხშირად გამოიყენება უბრალო ბუნებრივი სისტემები, რომლებშიც მიუხედავად გარემოსთან სითბური გაცვლისა, ტემპერატურა უცვლელი რჩება - ასეთია წყლისა და ყინულის ნარევი და წყლისა და ორთქლის ნარევი დუღილისა ნორმალური ატმოსფერული წნევის პირობებში. ცელსიუსის ტემპერატურული შკალის მიხედვით ყინულის დნობის წერტილი მიეწერება 0 °С-ს, დუღილის წერტილი კი – 100 °С. თერმომეტრის კაპილარში სითხის სვეტის სიმაღლის ცვლილება 0 °С-სა და  100 °С-სის ჩვენებებს შორის  სირძის ერთი მეასედით მოღებულია 1 °С-ს ტოლად. ზოგ ქვეყანაში (აშშ) ფართოდ გამოიყენება ფარენჰეიტის შკალა (T_F), სადაც წყლის გაყინვის ტემპერატურად მიღებულია 32 °F, ხილო წყლის დუღილის ტემპერატურად 212 °F. აქედან გამომდინარე:

\(T_{F}=\frac{9}{5}T_{C}+32^{\circ}\) ან \(T_{C}=\frac{5}{9}(T_{F}-32^{\circ}).\)

ფიზიკაში განსაკუთრებული ადგილი აირის თერმომეტრებს უკავიათ (ნახ. 4), რომლებშიც ტერმომეტრულ ნივთიერებას უცვლელი მოცულობის (\(V=const\)) ჭურჭელში მოთავსებული გათხევადებული აირი (ჰელიუმი, ჰაერი) წარმოადგენს, თერმომეტრული სიდიდე კი - აირის წნევაა \(p\). ცდები უჩვენებენ, რომ აირის წნევა (როცა \(V=const\)) ტემპერატურის (იზომება ცელსიუსის შკალით)  ზრდასთან ერთად იზრდება.

ნახ. 4.

მუდმივი მოცულობის აირის თერმომეტრი.

 

მუდმივი მოცულობის აირის თერმომეტრიs დასაგრადუირებლად შეიძლება გაიზომოს წნევა ტემპერატურიs ორ მნიშვნელობას  შორის (მაგ., 0 °C და 100 °C), დავიტანოთ p₀ და p₁₀₀ წერtილები გაფიკზე და მათ შორის გავატაროთ წრფე (ნახ. 5). ამგვარად მიღებული კალიბრების მრუდის გამოყენებით შეიძლება წნევის სხვა მნიშვნელობების შესაბამისი ტემპერატურები განისაზღვროს. ამ მრუდის დაბალი წნევებისკენ ექსტრაპოლირებით შეიძლება განისაზღვროს რაღაც „ჰიპოთეტური“ ტემპერატურა, რომლებზედაც აირის წნევა ნული გახდებოდა. ცდები უჩვენებემ, რომ ეს ტემპერატურა –273,15 °С-ს ტოლია და აირის თვისებებზეა დამოკიდებული. ცდის საშუალებით აირის გაციება წნევის ნულოვან დონემდე შეუძლებელია, რადგან ძალიან დაბალი ტემპერატურებისას ყველა აირი თხევად ან მყარ მდგომარეობაში გადადის.

ნახ. 3.2.5.

აირის წნევის ტემპერატირაზე დამოკიდებულება როცა  \(V=const\).

 

ინგლისელმა ფიზიკოსმა კელვინმა 1848 წელს აირის ნულოვანი წნევის წერტილი გამოიყენა ახალი ტემპერატურული შკალის ასგებად (კელვინის შკალა). ამ შკალაში გაზომვის ერთეული ისეთივეა როგორიც ცელსიუსის შკალაზე, მაგრამ გადაწეულია ნულოვანი წერტილი:

\(T_{K}=T_{C}+273,15.\)

\(Si\) სისტემაში მიღებულია, რომ  კელვინის შკალით გაზომილი ტემპერატურის ერთეულს კელვინი ეწოდება და აღინიშნება \(K\)ასოთი. მაგალითად, ოთახის ტემპერატურა T_С = 20 °С კელვინის შკალით ტოლია T_К = 293,15 К.

კელვინის ტემპერატურულ შკალას ტემპერატურის აბსოლუტურ შკალას უწოდებენ. იგი ყველაზე მოსახერხებელია ფიზიკური თეორიეების აგებისათვის.

არ არსებობს კელვინის შკალის ორ ფიქსირებულ წერტილთან, ყინულის დნობისა და ნორმალური ატმოსფერული წნევის დროს წყლის დუღულის წერტილთან, მიბმის აუცილებლობა, ცელსიუსის შკალის მსგავსად.

აირის ნულოვანი წნევის წერტილის გარდა, რომელსაც ტემპერატურის აბსოლუტურ ნულს უწოდებენ, საკმარისისა კიდევ ერთი, ფიქსირებულლი საყრდენი წერტილის არჩევა. კელვინის შკალაზე ასეთ წერტილად გამოიყენება წყლის სამმაგი ტემპერატურის წერტილი (0,01 °С), რომელშიც სითბურ წონესწორობაში სამივე ფაზა - ყინული, წყალი, ორთქლი - იმყოფება. კელვინის შკალით სამმაგი ტემპერატურის წერტილი მიღებულია  273,16 К-ს ტოლად.

აირის თერმომეტრები დიდი ზომისაა და მოუხერხებელია: ისინი პრეცესიულ სტანდარტად გამოიყენება სხვა თერმომეტრების კალიბრირებისათვის (დასაყალიბებად).

ამგავარად, მუდმივი \(V\) მოცულობის ჭურჭელში გაიშვიათებილი აირის წნევა მისი აბსოლუტური ტემპერატურის პირდაპირპროპორციულია:  \(p\sim T\). მეორეს მხრივ, ცდები უჩვენებენ,  მუდმივი \(V\) მოცულობის და \(T\) ტემპერატურისას წნევა პირდაპირპროპორციულია მოცემულ ჭურჭელში ნივთიერების \(\nu\) რაოდენობის ფარდობისა ამ ჭურჭლის \(V\) მოცულობასთან:

\(p\sim \frac{\nu}{V}=\frac{N}{N_{A}V}=\frac{n}{N_{A}}\sim n,\)

სადაც \(N\) – ჭურჭელში მოლეკულების რიცხვია, \(N_{A}\) – ავოგადროს მუდმივა, \(n=\frac{N}{V}\) – მოლეკულების კონცენტრაცია (ე.ი. მოლეკულების რიცხვი მოცულობის ერთეულში). ამ ფარდობების პროპორციებში გაერთიანებით შეიძლება ჩაიწეროს: 

\(p=nkT\),

სადაც \(k\) - ყველა აირისათვის საერთო გარკვეული მოდმივაა. მას ბოლცმანის მუდმივას უწოდებენ, მოლეკულირ-კინეტიკური თეორიის ერთ-ერთი შემქმნელი ავსტრიელი ფიზიკოსის ბოლცმანის საპატივცემლოდ. ბოლცმანის მუდმივა ერთ-ერთი ფუნდანენტური ფიზიკური მიდმივაა. მისი მნიშვნელობა \(Si\) სისტემაში ტოლია:

k = 1,38·10^–23 ჯ/К.

\(p=nkT\)-ს შედარებით აირების მოლეკულურ-კინეტიკური თეორიის ძირითად განტოლებასთან, შეიძლება მივიღოთ:

\(\bar{E_{k}}=\frac{3}{2}kT.\)

აირების მოლეკულების ქაოსური მოძრაობის საშუალო კინეტიკური ენერგია აბსოლუტური ტემპერატურის პირდაპირპროპორციულია.

ამგვარად, ტემპერატურა მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკური ენერგიის ზომაა.

საყურადღებოა, რომ მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკური ენერგია არაა დამოკიდებული მის მასაზე. სითხეში ან აირში შეწონილი ბროუნის ნაწილაკს ისეთივე კინეტიკური ენერგია აქვს, როგორიც ცალკეულ მოლეკულას, რომელსაც ბროინის ნაწილაკზე მრავალი რიგით ნაკლები მასა აქვს. ეს დასკვნა ვრცელდება იმ შემთხვევაზეც როცა ჭურჭელში მოთავსებულია აირების ნარევი, რომლების ქიმიურად არ ურთიერთქმედებენ და რომელთა მოლეკულებსაც განსხვავებული მასები აქვთ. წონასწორობის მდგომარეობაში სხვდასხვა აირების მოლეკკულებს სითბური მოძრაობის ერთნაირი საშუალო კინეტიკური ენერგია აქვთ, რომელიც მხოლოს ნარევის ტემპერატურით განისაზღვრება. ჭურჭლის კედლებზე ნარევის წნევა წარმოადგენს თითოეული აირის პარციალური წნევეათა ჯამს:

\(p=p_{1}+p_{2}+p_{3}+...=(n_{1}+n_{2}+n_{3}+...)kT.\).

ამ ფორმულაში \(n_{1},n_{2},n_{3}+...\) – ნარევის შემადგენელი სხვადსხვა აირის კონცენტრაციებია. ეს ფორმულა მოლეკულურ-კინეტიკური თეორიის ენაზე გადმოსცემს XIX საუკუნის დასაწყისში ექსპერიმენტულად დადგენილ დალტონის კანონს:  ისეთი აირების ნარევის წნევა, რომლებიც ქიმიურად არ ურთიერთქმედებენ, მათი პარციალური წნევების ჯამის ტოლია.

{loadnavigation}

მოლეკულურ-კინეტიკური თეორიას უწოდებენ სწავლებას ნივთიერების აგებულებისა და თვისებების შესახებ, რომელსაც საფუძვლად უდევს წარმოდგენა, რომ ატომები და მოლეკულები ქიმიური ელემენტების უმცირეს შემადგენელი ნაწილაკებს წარმოადგენენ.

მოლეკულურ-კინეტიკური თეორიის საფუძველს სამი ძირითადი დებულება წარმოადგენს:

1) ყველა ნივთიერება -თხევადი, მაყარი და აირები - შედგება უმცირესი ნაწილაკების - მოლეკულებისგან, რომლების თვითონ ატომებისგან შედგებიან („ელემენტარული მოლეკულები“). ქიმიური ელემენტების მოლეკულები შეიძლება იყოს მარტივი და რთული, ე.ი შედგებოდეს ერთი ან რამდენიმე ატომისგან. მოლეკულები და ატომები ელექტრულად ნეიტრალურ ნაწილაკებს წარმოადგენენ. გარკვეულ პირობებში მოლეკულებს და ატომებს შუძლეათ შეიძინონ დამატებითი ელეტრული მუხტი და გადაიქცნენ დადებით ან უარყოფით იონებად.

2) ატომები და მოლეკულები მუდმივ, ქაოსურ მოძრაობაში არიან.

3) ნაწილაკები ერთმანეთთან ურთიერთქმედებენ ძალებით. რომლებსაც ელექტრული ბუნება აქვთ. ნაწილაკებს შორის გარავიტაციული ურთიერთქმედება იმდენად უმნიშვნელოა,რომ შესაძლებელია უგულვებელყოფა.

ნახ.1.

ბროუნის ნაწილაკების ტრაექტორიები

ატომებისა და მოლეკულების ქაოსური მოძრაობის შესახებ მოლეკულურ-კინეტიკური თეორიის წარმოდგენის საუკეთესო ექსპერიმენტულ დასაბუთებას ბროუნის მოძრაობა წარმოადგენს.

იგი სითხესა და აირში შეწონილი უმცირესი მიკროსკოპული ნაწილაკების სითბური მოძრაობაა. აღმოაჩინა ინგლისელმა ბოტანიკოსმა ბროუნმა 1927 წ. ბროუნის ნაწილაკები მოძრაობენ მოლეკულებთან უსასრულო შეჯახებების ხარჯზე. მოლეკულების ქაოსური სითბური მოძრაობის გამო ეს დაჯახებები არასოდეს არ აწონესწორებენ ერთმანეთს. ამის შედეგად ბროუნის ნაწილაკების სიჩქარეები უწესრიგოდ იცვლიან სიდიდესა და მიმართულებას, მათი ტრაექტორიები კი რთულ, ზიგზაგებისგან შედგენილ მრუდებს წარმოადგენენ (ნახ.1.). ბროუნის მოძრაობის თეორია აინშტაინის მიერ იქნა შექმნილი 1905წ. ანშტაინის თეორია ექსპერიმენტულად დაადასტურა ფრანგმა ფიზიკოსმა პერენმა 1908-1911წწ.

ანშტაინის თეორიის მთავარი დასკვნა იმაში მდგომარეობს, რომ ბროუნი ნაწილაკს საწყისი მდებარეობიდან წანაცვლების კვადრატი \(<r^{2}>\)E  , რომელიც მრავალი ბროუნის ნაწილაკის წანაცვლების გასაშუალოებითაა მიღებული, დაკვირვების \(t\) დროის პროპორციულია.   

\(<r^{2}>=Dt.\)

ეს ფორმულა ე.წ. დიფუზურ კანონს გამოსახავს. თეორიის მოხედვით \(D\) კოეფიციენტი ტემპერეტურის ზრდასთან ერთად მონოტონურად იზრდება.

მოლეკულების მუდმივი ქაოსური მოძრაობა თავს იჩენს აგრეთვე, სხვა ადვილად დაკვირვებად მოვლენეში, რომელსაც დიფუზია წოდება.

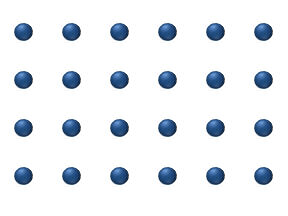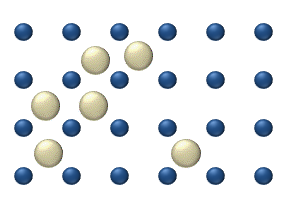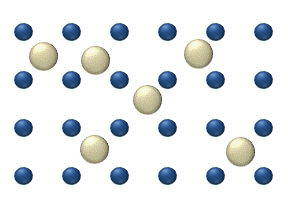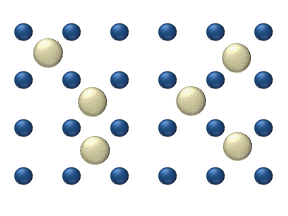
დიფუზია ეწოდება ორი ან რამოდენიმე ურთიერთშეხებაში მყოფი ნივთიერების ერთმანეთში შეღწევის მოვლენას. ყველაზე სწრაფად ეს პროცესი ისეთ აირში მიმდინარეობს, რომელის შედგენილობის მხრივ არაერთგვაროვანია.  კომპონენტების სიმკვრივის მიუხედავად დიფუზიის შედეგად ერთგვაროვანი ნარევი მიიღება. მაგალითად, თუ გადატიხრული ჭურჭლის ორ  ნაწილში იმყოფება ჟანგბადი \(O_{2}\) და წყალბადი \(H_{2}\),  ტიხრის მოშორების შემდეგ იწყება ერთმანეთში შეღწევის პროცესი, რასაც ფეთქებადსაშიში ნარევის მიღება მოჰყვება. ეს პროცესი მაშინაც მიმდინარეობს, როცა მსუბუქი აირი (წაყალბადი) ჭურჭლის ზედა ნახევარში იმყოფება, უფრო მძიმე კი ქვედა.

სითხეებში ეს პროცესი გაცილებით ნელა მიმდინარობს. ორი სხვადასხვაგვარი სითხის ურთიერთშეღწევა, მყარი  ნივთიერების სითხეში გახსნა (მაგ: შაქარი წყალში) და ერთგვაროვანი ხსნარის წარმოქმნა - სითხეში დიფუზიის მაგალითებია.

რეალურ პირობებში დიფუზია აირებსა და სითხეებში შენიღბულია უფრო ჩქარი შერევის პროცესებით, მაგალითად, კონვექციური დინებების წარმოქმნის გამო.

დიფუზიის ყველაზე ნელი პროცესი მყარ სხეულებში მიმდინარეობს. მაგრამ, ცდები უჩვენებენ, რომ კარგად გაპრიალებული ორი მეტალური ზედაპირის ხანგრძლივი კონტაქტის შედეგად ორივეში შეიძლება აღმოვაჩინოთ მეორე მეტალის ატომები.

დიფუზია და ბროუნის მოძრაობა მსგავსი მოვლენებია. შეხებაში მყოფი ნივთიერებების ურთიერთშეღწევა და სითხესა და აირში შეწონილი უმცირესი ნაწილაკების ქაოსური მოძრაობა მოლეკულების სითბური ქაოსური მოძრაობის შედეგია.

ორ მოლეკულას შორის მოქმედი ძალა მათ შორის მანძილზეა დამოკუდებული. მოლეკულები რთულ სივრცულ სტრუქტურებს წარმოადგენენ, რომლებიც როგორც დადებით, ასევე უარყოფით იონებს შეიცავენ. თუ მოლეკულებს შორის მანძილი საკმარისად დიდია, მაში მოლეკულებს შორის მიზიდულობის ძალები ჭარბობს, მცირე მანძილებზე კი ჭარბობს განზიდვის ძალები. ჯამური F ძალისა და მოლეკულებს შორის ურთიერთქმედების პოტენციური ენერგიის \(E_{p}\) სიდიდეებიდან დამოკუდებულება მოლეკულების ცენტრებს შორის მანძილებძე ნაჩვენებია ნახ. 2-ზე. რაღაც \(r=r_{0}\) მანძილზე ურთიერთქმედების ძალა ნულის ტოლი ხდება. ეს მანძილი, პირობითად, შეიძლება მივიღით მოლეკულის დიამეტრის ტოლად. ურთიერთქმედების პოტენციური ენერგია \(r=r_{0}\) -სთვის მინიმალურია. ერთმანეთისგან \(r_{0}\) მანძილეზე მყოფი ორი მოლეკულის ერთმანეთისგან დასაცილებლად მათ უნდა მივანიჭოთ დამატებითი ენერგია \(E_{0}.\) \(E_{0}\) სიდიდეს პოტენციური ორმოს სიღრმეს ან კავშირის ენერგიას უწოდებენ.

ნახ. 2.

ორი მოლეკულის ურთიერთქმედების \(F\) ძალა და ურთიერთქმედების პოტენციური \(E_{p}\) ენერგია. \(F>0\)– განზიდვის ძალა, \(F<0\) – მიზიდვის ძალა.

 

მოლეკულებს უკიდურესად მცირე ზომები აქვთ. მარტივი, ერთატომიანი მოლეკულების ზომები  10^–10 მ რიგისაა. რთულ, მრავალატომიან მოლეკულებს შეიძლება ჰქონდეთ ასობით და ათასობით უფრო დიდი ზომები.

მოლეკულების მოუწესრიგებელ ქაოსურ მოძრაობას სითბურ მოძრაობას უწოდებენ. სითბური მოძრაობის კინეტიკური ენერგია ტემპერატურის ზრდით იზრდება. დაბალი ტემპერატურებისთვის მოლეკულების საშუალო კინეტიკური ენერგია შეიძლბა პოტენციური ორმოს \(E_{0}\) სიღრმეზე დაბლა აღმოჩნდეს. ასეთ სემთხვევასი მოლეკულები კონდენსირდებიან თხევად ან მყარ ნივთიერებად; ამასთან მოლეკულებს შორის საშუალო მანძილი დახლოებით r₀-ის ტოლია. ტემპერატურის გაზრდისას მოლეკულების საშუალო კინეტიკური ენერგია  \(E_{0}\)-ს აჭარბებს, მოლეკულები იფანტებიან, და წარმოიქმნება აირადი ნივთიერება.

მყარ სხეულებშო მოლეკულები ქაოსურ მოძრაობას ასრულებენ ფიქსირებული ცენტრების (წონასწორობის ადგილების) მახლობლობაში. ეს ცენტრები სივრცეში შეიძლება არარეგულარულად იყვნენ განლაგებული (ამორფული სხეულები) ან ქმნიდნენ მოწესრიგებულ მოცულობით სტრუქტურებს (კრისტალური სხეულები).

სითხეებში მოლეკულებს მნიშვნელოვნად დიდი თავისუფლება აქვთ სითბური მოძრაობისთვის. ისინ გარკვეულ ცენტრებთან არ არიან დაკავშირებული და შეუძლიათ გადაადგილება სითხის მთელ მოცულობაში. ამითი აიხსნება სითხეების დენადობა. ახლომდებარე სითხის მოლეკულებსაც შეუძლიათ წარმოქმნან რამდენიმე მოლეკულისგან შემდგარი მოწესრიგებული სტრუქტურები. ამ მოვლენას ახლო წესრიგს უწოდებენ, კრისტალური სხეულებისათვის დამახასიათემელი შორი წესრიგისგან განსხვავებით.

აირებში მოლეკულებს შორის მანძილი, ჩვეულებრივ მნიშვნელოვნად მეტია მათ ზომებზე. მოლეკულებს შორის ურთიერთქმედების ძალები ასეთ დიდ მანძილებძე მცირეა, და ყოველი მოლეკულა წრფის გასწვრივ მოძრაობს სხვა მოლეკულასთან ან ჭურჭლის კედელთან შემდგომ დაჯახებამდე. ნორმალურ პირობებში ჰაერის მოლეკულებს შორის საშუალო მანძილი 10^–8 რიგისაა, ე.ი. ათეულობით აჭარბებს მოლეკულების ზომებს. მოლეკულებს შორის სუსტი ურთიერთქმედებით აიხსნება აირების გაფართოების და ჭურჭლის მთელი მოცულობის დაკავების თვისება. ზღვარზე, სადაც ურთიერთქმედება ნულისკენ მიისწრაფის, ჩვენ მივდივართ იდეალური აირის წარმოდგენამდე.

მოლეკულურ-კინეტიკურ თეორიაში ნივთიერების რაოდენობა ნაწილაკების რიცხვის პროპორციულადაა მიღებული. ნივთიერების რაოდენობის ერთეულს მოლი ეწოდება.

მოლი - ნივთიერების ის რაოდენობაა, რომელიც იმდენივე ნაწილაკს (მოლეკულას) შეიცავს, რამდენ ატომსაც შეიცავს 0,012 კგ ნახშირბადი \(^{12}C\). ნახშირბადის მოლეკულა ერთი ატომისაგან შედგება.

ამგვარად, ნებისმიერი ნივთიერების ერთი მოლი შეიცავს ერთიდაიგივე ნაწილაკების (მოლეკულების) რაოდენობას. ამ რიცხვს ავოგადროს მუდმივას  \(N_{A}\) უწოდებენ:

\(N_{A}=6,02\cdot 10^{23}\) მოლი^–1

ავოგადოს მუდმივა - მოლეკულურ-კინეტიკური თეორიის ერთ-ერთი უმნიშვნელოვანესი მუდმივაა.

ნივთიერების რაოდენობა \(\nu\) განისაზღვრება როგორც ნაწილაკების (მოლეკულების) რიცხვის \(N\) ფარდობა ავოგადროს \(N_{A}\) მუდმივასთან:

 \(\nu=\frac{N}{N_{A}}.\)

ერთი მოლი ნივთიერების მასას \(M\)  მოლურ მასას უწოდებენ. მოლერი მასა ტოლია ნივთიერების ერთი მოლეკულის მასის ნამრავლისა ავოგადროს მუდმივაზე:

\(M=N_{A}\cdot m_{0}.\)

მოლური მასა გამოისახება კგ/მოლი სიდიდით. ერთი ატომისაგან შედგენილი მოლეკულების მქონე ნივთიერებისათვის ხშირად იყენებეს ტერმინს ატომური მასა.

ატომებისა და მოლეკულების მასის ერთეულად მოღებულია ნახშირბადის \(^{12}C\) იზოტოპის (მასური რიცხვი 12) ატომის მასის 1/12. ამას მასის  ატომურ ერთეულს უწოდებენ.

1 მ.ა.ე. = 1,66·10^–27 კგ.

ეს სიდიდე თითქმის ემთხვევა პროტონის ან ნეიტრონის მასას. მოცემული ნივთიერების ატომის ან მოლეკულის მასის ფარდობას ¹²C ნახშირბადის ატომის მასის 1/12-თან ფარდობით მასას უწოდებენ.

{loadnavigation}

მოლეკულური ფიზიკა და თერმოდინამიკა, მათი მიდგომის მიხედვით, ძირითადად ორი სხვადასხვა  მაგრამ ერთმანეთთან მჭიდროდ დაკავშირებული მეცნიერებაა. ისინი ორივე ერთიდაიგივეს, ფიზიკური სისტემების მაკრისკოპულ თვისებებს შეისწავლის, მაგრამ სრულიად განსხვავებული მეთოდებით.

მოლეკულარული ფიზიკის ანუ მოლეკულურ-კინეტიკური თეორიის საფუძველში ნივთიერების აგებულების შესახებ გარკვეული წარმოდგენა დევს. ნაწილაკების უამრავი რიცხვისგან შემდგარი მაკროსკოპული სისტემის ყოფაქცევის დასადგენად მოლეკულურ ფიზიკაში გამოიყენება ნივთიერების სხვადასხვა მოდელები, მაგალითად, იდეალური აირის მოდელი.

მოლეკულური ფიზიკა სტატისტიკურ თეორიას წარმოადგენს, ე.ი. თეორიას, რომელიც უამრავი რიცხვისაგან შედგენილ სისტემის ყოფაქცევას განიხილავს ალბათური მოდელების საფუძველზე. იგი ცდილობს სტატისტიკური მიდგომით დაადგინოს კავშირი ექსპერიმენტულად გაზომილ მაკროსკოპულ სიდიდეებსა (წნევა, მოცულობა ტემპერატურა და სხვა) და სისტემის შემადგენელი ნაწილაკების მიკროსკოპულ მახასიათებლებს (მასა. იმპულსი, ენერგია და სხვა) შორის.

მოლეკულურ-კინეტიკური თეორიისგან განსხვავებით, თერმოდინამიკა მაკროსკოპოლი სისტემის თვისებების შესწავლისას არ ეყრდნობა ნივთიერების მოლეკულური სტრუქტურის შესახებ რაიმე წარმოდგენას. თერმოდინამიკა ფენომენოლოგიურ მეცნიერებას წარმოადგენს. იგი ნივთიერების თვისებების შესახებ დასკვნებს ცდით დადგენილი კანონების საფუძველზე აკეთებს, მაგალითად როგორიცაა ენერგიის შენახვის კანონი. თერმოდინამიკა ოპერირებს მხოლოდ მაკროსკუპული სიდიდეებით  (წნევა, მოცულობა ტემპერატურა და სხვა), რომლებიც შემოტანილია ფიზიკური ექსპერიმენტის საფუძველზე.

ორივე მიდგომა - თერმოდინამიკური და სტატისტიკური - კი არ ეწინააღმდეგება, არამედ ავსებს ერთმანეთს. თერმოდინამიკის და მოლეკულურ-კინეტიკური თეორიის მხოლოდ ერთდროული  განხილვა იძლევა რაც შეიძლება სრულ წარმოდგენას ნაწილაკების უამრავი რიცხვისაგან შედგენილი მაკროსკოპული სისტემის თვისებების შესახებ.