{loadnavigation}
მექანიკური ენერგიის და იმპულსის შენახვის კანონები ისეთი ამოცანების ამოხსნის საშუალებას იძლევა, რომლებშიც მომქმედი ძალები ცნობილი არ არის. ამგვარი ამოცანის მაგალითი სხეულების დარტყმითი ურთიერთქმედებაა.
სხეულების დარტყმითი ურთიერთქმედებასთან საქმე შეიძლება ხშირად გვქონდეს ყოველდღიურ ცხოვრებაში, ტექნიკასა და ფიზიკაში (განსაკუთრებით ატომებისა ელემენტარული ნაწილაკების ფიზიკაში).
დარტყმა (ან შეჯახება ) მიღებულია ვუწოდოთ სხეულების ხანმოკლე ურთიერთქმედებას, რომლის შედეგადაც მათი სიჩქარეები მნიშვნელონად იცვლება. შეჯახებისას სხეულებს შორის მოქმედებს ხანმოკლე დარტყმითი ძალები, რომელთა სიდიდეები, როგორც წესი, უცნობია. ამიტომ დარტყმითი ურთიერთქმედების განხილვა უშუალოდ ნიუტონის კანონების გამოყენებით შეუძლებელია. მექანიკური ენერგიისა და იმპულსის შენახვის კანონები გამოყენება, ბევრ შემთხვევაში, საშუალებას იძლევა განხილვიდან გამოვრიცხოთ თვით შეჯახების პროცესი და სიჩქარეების ყველა სხვა შუალედური მნიშვნელობის გამოტოვებით, მივიღოთ კავშირი სხეულების საწყის და საბოლოო სიჩქარეებს შორის.
მაქანიკაში ხშირად გამოიყენება დარტყმითი ურთიერთქმედების ორი მოდელი – აბსოლუტურად დრეკადი და აბსოლუტურად არადრეკადი დარტყმები.
აბსოლუტურად არადრეკადი დარტყმისას მექანიკური ენერგია არ ინახება. იგი სრულად ან ნაწილობრივ გადადის სხეულის შინაგან ენერგიაში (გათბობა).
აბსოლუტურად არადრეკადი დარტყმის მაგალითად გამოდგება ბალისტიკურ ქანქარასთვის ტყვიის (ან ჭურვის) მორტყმა. ბალისტიკური ქანქარა \(M\) მასის ქვიშით სავსე, ბაწარზე დაკიდებული ყუთია (ნახ. 1). \(\vec{v}\) სიჩქარით მოძრავი \(m\) მასის ტყვია ხვდება ყუთს და რჩება მასში. ქანქარის გადახრის საშუალებით სეიძლება ტყვიის სიჩქარის გამოთვლა.
ყუთის სიჩქარე მასში ჩარჩენილ ტყვიასთან ერთად ავღნიშნოთ \(\vec{u}\) –თი. მაშინ, იმპულსის შენახვის კანონის მიხედვით
\(mv=(M+m)u;\: u=\frac{m}{M+m}v.\)
ტყვიის ყუთში ჩარჩენისას მოხდა მექნიკური ენერგიის დაკარგვა:
\(\Delta E=\frac{mv^{2}}{2}-\frac{(M+m)u^{2}}{2}=\frac{M}{M+m}\frac{mv^{2}}{2}.\)
ფარდობა \(\frac{M}{M+m}\) –ტყვიის მექნიკური ენერგიის შინაგან ენერგიად გარდაქმნილი ნაწილია.
\(\frac{\Delta E}{E_{0}}=\frac{M}{M+m}=\frac{1}{1+\frac{m}{M}}.\)
ეს ფორმულა სამართლიანია არა მხოლოს ბალისტიკური ქანქარისათვის, არამედ ორი სხვადასხვა მასის სხეულის ნებისმიერი არადრეკადი შეჯახების შემთხვევაში.
როცა \(m<<M\), \(\frac{\Delta E}{E_{0}}\rightarrow 1\) ტყვიის კინეტიკური ენერგია თითქმის მთლიანად გარდაიქმნება შინაგან ენერგიად. როცა \(m=M\), \(\frac{\Delta E}{E_{0}}\rightarrow \frac{1}{2}\) – შინაგან ენერგიად გარდაიქმნება ტყვიის საწყისი კინეტიკური ენერგიის ნახევარი. და ბოლოს, დიდი მასის მოძრავი სხეულის მცირე მასის უძრავ სხეულთან (\(m>>M\)) არადრეკადი შეჯახებისას ფარდობა \(\frac{\Delta E}{E_{0}}\rightarrow 0.\)
ქანქარის შემდგომი მოძრაობა შეიძლება გამოვთვალოთ ენერგიის შენახვის კანონის საშუალებით:
\(\frac{(M+m)u^{2}}{2}=(M+m)gh;\: u^{2}=2gh,\)
სადაც \(h\)– ქანქარის გადახრის მაქსიმალირი სიმაღლეა. ამ ფორმულებიდან გამოდის:
\(v=\frac{M+m}{m}\sqrt{2gh}.\)
ცდით საშუალებით \(h\) სიმაღლის გაზომვით, შეიძლება განისაზღვროს ტყვიის \(v\) სიჩქარე.
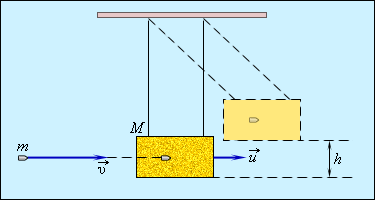
ნახ. 1.
ბალისტიკური ქანქარა
აბსოლუტურად დრეკად დარტყმას უწოდებენ შეჯახებას, რომლის დროსაც ინახება მექანიკური ენერგია.
ბევრ შემთხვევაში ატომების, მოლეკულების და ელემენტარული ნაწილაკების შეჯახება აბსოლურურად დრეკადი დარტყმის კანონებს ემორჩილება.
აბსოლურურად დრეკადი დარტყმის იმპულსის შენახვის კანონთან ერთად მექანიკური ენერგიის კანონიც სრულდება.
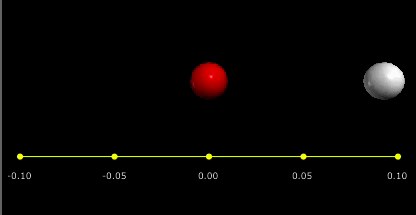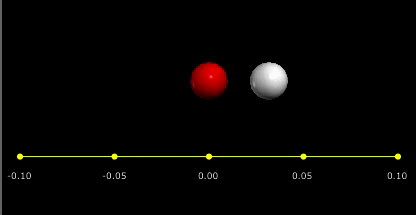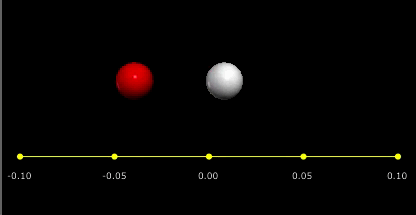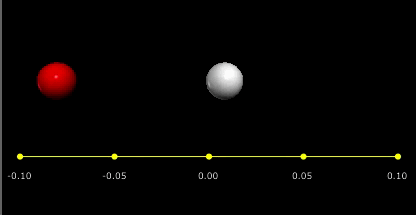
აბსოლურურად დრეკადი დარტყმის უბრალო მაგალითს ბილიარდის ორი ბურთულის ცენტრალური დარტყმა წარმოადგენს, როცა ერთ–ერთი მათგანი უძრავია (ნახ. 2).
ბურთულების ცენტრალურ დარტყმას ისეთ შეჯახებას უწოდებე, როცა ბურთულების სიჩქარეები დარტყმამდე და დარტყმის შემდეგ ცენტრებზე გამავალი წრფის გასწვრივაა მიმართული.

ნახ. 2.
აბსოლურურად დრეკადი ცენტრალურ დარტყმა
ზოგად შემთხვევაში შეჯახებაში მონაწილე ბურთულების მასები \(m_{1}\) და \(m_{2}\) შეიძლემა არ იყოს ერთნაირი. მექანიკური ენერგიის შენახვის კანონის თანახმად
\(\frac{m_{1}v_{1}^{2}}{2}=\frac{m_{1}u_{1}^{2}}{2}+\frac{m_{2}u_{2}^2}{2}.\)
სადაც \(v_{1}\) – პირველი ბურთულის სიჩქარეა შეჯახებამდე, მეორე ბურთულისთვის სიჩქარე \(v_{2}=0\), \(v_{1}\) და \(v_{2}\) – სიჩქარეები დაჯახების შემდეგ. იმპულსის შენახვის კანონი სიჩქარის გეგმილებში ღერძზე, რომელიც მოძრავი ბურთულის შეჯახებამდე სიჩქარის გასწვრივაა მიმართული, ასე ჩაიწერება:
\(m_{1}v_{1}=m_{1}u_{1}+m_{2}u_{2}\).
მივიღეთ განტოლებათა სისტემა. ამ სისტემის ამოხსნით ვიპოვით უცნობ \(u_{1}\) და \(u_{2}\) სიჩქარეებს
\(u_{1}=\frac{(m_{1}-m_{2})v_{1}}{m_{1}+m_{2}};\: u_{2}=\frac{2m_{1}v_{1}}{m_{1}+m_{2}}.\)
კერძო შემთხვევაში, როცა ორივე ბურთულას ერთნაირი მასა აქვს (\(m_{1}=m_{2}\)), პირველი ბურთულა ჩერდება (\(u_{1}=0\)), მეორე მოძრაობს სიჩქარით \(u_{2}=v_{1}\), ე.ი. ბურთულები სიჩქარეებს ცვლიან (და, ე.ი იმპულსებსაც).
თუ შეჯახებამდე მეორე ბურთულას ჰქონდა ნულისაგან განსხვავებული სიჩქარე (\(v_{2}\neq 0\)), ამ ამოცანის დაყვანა ადვილად შეიძლება წინა ამოცანაზე ახალი ათვლის სისტემაზე გადასვლით. რომელიც υ2 სიჩქარით წრფივად და თანაბრად მოძრაობს „უძრავი“ სისტემის მიმართ. ამ სისტემაში მეორე ბურთულა შეჯახებამდე უძრავია, ხოლო პირველი მოძრაობს \(v_{1}^{'}=v_{1}-v_{2}\) სიჩქარით. ზემოთ მოყვანილი ფორმულებით \(u_{1}\) და \(u_{2}\) სიჩქარეების ახალ სისტემაში განსაზღვის შემდეგ, უნდა გადავიდეთ ისევ „უძრავ“ სისტემაზე.
ამგვარად, მექანიკური ენერგიისა და იმპულსის მუდმივობის კანონების გამოყენებით, შეიძლენა განვსაზღვროთ ბურთულების სიჩქარეები შეჯახების შემდეგ, თუ ცნობილია მათი სიჩქარეები შეჯახებამდე.
ცენტრალური შეჯახება პრაქტიკაში ძალიან იშვიათად ხდება, მით უფრო, თუ საქმე ატომებისა და მოლეკულების შეჯახემას შეეხება. არაცენტრალური დრეკადი დაჯახებისას ნაწილაკების (ბირთვების) სიჩქარეები დაჯახებამდე და დაჯახების შემდეგ ერთი წრფის გასწვრივ არაა მიმართული.
არაცენტრალური დრეკადი დაჯახების კერძო შემთხვევას წარმოადგენს ბილიარდის ორი ერთნაირი მასის ბურთულის შეჯახება, როცა შეჯახებამდე ერთი მათგანი უძრავია, ხოლო მეორის სიჩქარე მიმართული არ იყო ბურთულების ცენტრების შემაერთებელი წრფის გასწბრივ (ნახ. 3).

ნახ. 3.

ორი ერთნაირი მასის ბურთულის არაცენტრალური დრეკადი დაჯახება. \(d\)– დამიძნების მანძილი
არაცენტრალური დაჯახების შემდეგ ბურთულები ერთმანეთის მიმართ გარკვეული კუთხით მოძრაობენ. შეჯახების შემდგომი სიჩქარეების \(\vec{u_{1}}\) და \(\vec{u_{2}}\) განსაზღვრისათვის საჭიროა ბურთულების ცენტრების წრფეთა მდებარეობისა და დამიზნების \(d\) მანძილის ცოდნა (ნახ. 3), ე.ი. მანძილი ორ წრფეს შორის, როლებიც ბურთულების ცენტრებზე გადიან და მოძრავი ბურთულის \(\vec{v}_{1}\) სიჩქარის მიმართულების პარალელური არიან. თუ ბურთულების მასები ერთნაერია, მაშინ დრეკადი შეჯახების შემდეგ ბურთულების სიჩქარის ვექტორები \(\vec{u}_{1}\) და \(\vec{u}_{2}\) ყოველთვის ერთმანეთის მართობულადაა მიმართული. ეს ადვილი საჩვენებელია იმპულსისა და ენერგიის მუდმივობის კანონების გამოყენებით. როცა \(m_{1}=m_{2}=m\) ეს კანონები ღებულობენ სახეს:
\(\vec{v_{1}}=\vec{u}_{1}+\vec{u}_{2};\: \vec{v}_{1}^{2}=\vec{u}_{1}^{2}+\vec{u}_{2}^{2}.\)
პირველი ტოლობა ნიშნავს, როს სიჩქარის ვექტორები \(\vec{v}_{1}\), \(\vec{u}_{1}\) და \(\vec{u}_{2}\) ქმნიან სამკუთხედს (იმპულსების დიაგრამა), ხოლო მეორე – რომ, ამ სამკუთხედისათვის სამართლიანია პითაგორას თეორემა, ე.ი. მართკუთხაა. \(\vec{u}_{1}\) და \(\vec{u}_{2}\) კათეტებს შორის კუთხე 90° ტოლია.
{loadnavigation}
თუ ჩაკეტილი მექანიკური სისტემის სხეულები ურთიერთქმედებენ მხოლოდ მიზიდულობისა და დრეკადობის ძალების საშუალებით, მაშინ მათ მიერ შესრულებული მუშაობა, აღებული საწინააღმდეგო ნიშნით, ამ სხეულების პოტენციური ენერგიის ცვლილების ტოლია:
\(A=-(E_{p2}-E_{p1})\).
კინეტიკური ენერგიის თეორემის მიხედვით, ეს მუშაობა სხეულების კინეტიკური მუშაობის ცვლილების ტოლია:
\(A=E_{k2}-E_{k1}.\)
აქედან გამომდინარე:
\(E_{k2}-E_{k1}=-(E_{p2}-E_{p1})\Rightarrow E_{k1}+E_{p1}=E_{k2}+E_{p2}.\)
ჩაკეტილი მექანიკური სისტემის შემადგენელი და მიზიდულობისა და დრეკადობის ძალების საშუალებით ურთიერთქმედი სხეულების კინეტიკური და პოტენციური ენერგიების ჯამი უცვლელი რჩება.
ეს ფორმულირება მექანიკური პროცესებში ენერგიის მუდმივობის კანონს წარმოადგებს. ის ნიუტონის კანონების შედეგია. \(E=E_{k}+E_{p}\) ჯამს სრულ მექანიკურ ენერგიას უწოდებენ. მექანიკური ენერგიის მუდმივობის კანონი მხოლოდ მაშინ სრულდება, როცა სხეულები, ჩაკეტილ სისტემაში ურთიერთქმედებენ მხოლოდ კონსერვატული ძალებით, ე.ი. ძალებით რომელთათვისაც პოტენციური ენერგიის ცნების შემოღებაა შესაძლებელი.
ენერგიის შენახვის კანონის გამოყენების მაგალითია, იმ უჭიმვადი ძაფის მინიმალური სიმტკიცის პოვნა, რომელიც იჭერს მის ბოლოზე დამაგრებულ მასის სხეულს ბრუნვის ვერტიკალურ სიბრტყეში (ე.წ. ჰიუგენსის ამოცანა). ნახ. 1–ზე მოცემულია ამ ამოცანის განმარტება.
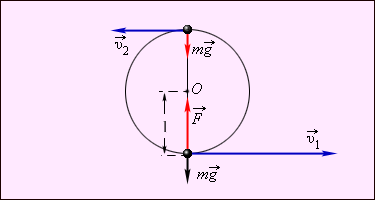
ნახ. 1.
ჰიუგენსის ამოცანა. \(\vec{F}\) – ძაფის დაჭიმულობის ძალა ტრაექტორიის ქვედა წერტილში
ენერგიის მუდმივობის კანონი სხეულისთვის ტრაექტორიის ქვედა და ზედა წერტილებში შემდეგი სახით ჩაიწერება:
\(\frac{mv_{1}^{2}}{2}=\frac{mv_{2}^{2}}{2}+mg2l.\)
ყურადღება მივაქციოთ იმას, რომ ძაფის დაჭიმულობის \(\vec{F}\) ძალა ყოველთვის სხეულის სიჩქარის მართობულია; ამიტომ ის მუშაობას არ ასრლებას.
ბრუნვის მინიმალირი სიჩქარისას ძაფის დაჭიმულობა ტრაექტორიის ზედა წერტილში ნულის ტოლია და, ე.ი. ცენტრისკენული აჩქარება სხეულს ენიჭება მხოლოდ სიმძიმის ძალის გავლენით:
\(\frac{mv_{2}^{2}}{l}=mg.\)
ამ დამოკიდებულებებიდან გამოდის:
\(v_{1\: min}^{2}=5gl.\)
ცენტრისკენული აჩქარება ტრაექტორიის ქვედა წერტილში განპირობებულია სხვადასხვა მხარეს მიმართული \(\vec{F}\) და \(m\vec{g}\) ძალებით:
\(\frac{mv_{1}^2}{2}=F-mg.\)
აქედან გამოდის, რომ სხეულის ზედა წერტილში მინიმალური სიჩქარის დროს ძაფის დაჭიმულობა ქვედა წერტილში მოდულით ტოლია
%F=6mg.$
ნათელია, რომ ძაფის სიმტკიცე ამ სიდიდეს უნდა აღემატებოდეს.
ძალიან მნიშვნელოვანია აღინიშნოს, რომ მექანიკური ენერგიის შენახვის კანონი სხეულის ტრაექტორიის ორ განსხვავებულ წერტილში მისი კოორდინატებსა და სიჩქარეებს შორის კავშირის მიღების საშუალებას იძლევა, ტრაექტორიის ყველა სხვა წერტილში სხეულის მოძრაობის კანონის ანალიზის გარეშე. მექანიკური ენერგიის შენახვის კანონის გამოყენაბას შეუძლია საგრძნობლად გაადვილოს მრავალი ამოცანის ამოხსნა.
რეალურ პირობებში კონსერვატული ძალების გვერდით ყოველთვის მოქმედებენ ხახუნის ან გარემოს წინააღმდეგობის ძალები.
ხახუნის ძალა არაა კონსერვატული, მისი მუშაობა განვლილი მანძილის სიგრძეზეა დამოკიდებული.
თუ ჩაკეტილი სისტემის სხეულებს შორის მოქმედებს ხახუნის ძალები, მაშინ მექანიკური ენერგია არ ინახება. მექანიკური ენერგიის ნაწილი სხეულების შინაგან ენერგიად გადაიქცევა (გათბობა).
ეს, ექსპერიმენტულად გადგენილი ფაქტი გამოხატავს ბუნების ფუნდამენტურ კანონს – ენერგიის შენახვისა და გარდაქმნის კანონს.
ენერგიის შენახვისა და გარდაქმნის კანონის ერთ–ერთ შედეგს წარმოადგებს „მუდმივი ძრავის“ (perpetuum mobile) შექმნის შეუძლებლობა – მანქანისა, რომელიც, ენერგიის დანახარჯის გარეშე, განუსაზღვრელად დიდი ხნის განმავლობაში შეძლებდა მუშაობის შესრულებას (ნახ. 2).
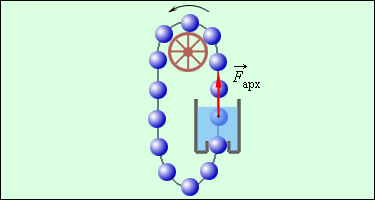
ნახ. 2.
„მუდმივი ძრავის“ ერთ–ერთი პროექტი. რატომ არ იმუშავებს ეს მანქანა?
ისტორია „მუდმივი ძრავის“ არა ერთ პროექტს ინახავს. ზოგ მათგანში „გამომგონებლის“ შეცდომა თვალნათლივ ჩანს, სხვებში ხელსაწყოს რთული კონსტრუქციის მიღმაა დაფარული და ხშირად ძნელი გასაგებია რატომ არ მუშაობს ეს მანქანა. „მუდმივი ძრავის“ შექმნის უნაყოფო ცდები ჩვენს დროშიც გრძელდება. ყველა ისინი მარცხისთვის არიან განწირულნი, რადგან ენერგიის შენახვისა და გარდაქმნის კანონი ენერგიის დახარჯვის გარეშე მუშაობის მიღებას „კრძალავს“.
{loadnavigation}
თუ \(m\) მასის სხეული მასზე მოდებული ძალების მოქმედებით მოძრაობს და მისი სიჩქარე \(v_{1}\)–დან \(v_{2}\)–მდე იცვლება, ძალები გარკვეული \(A\) მუშაობას ასრულებენ.
მოდებული ყველა ძალის მიერ შესრულებული სრული მუშაობა ამ ძალების ტოლქმედი ძალის მიერ შესრულებული მუშაობის ტოლია (ნახ. 1).

ნახ. 1.
ტოლქმედი ძალის მიერ შესრულებული მუშაობა.
\(A=F_{1}s\cos \alpha _{1}+F_{2}s\cos \alpha _{2}=F_{1s}s+F_{2s}s=F_{ps}s=F_{p}s\cos \alpha\)
სხეულის სიჩქარის ცვლილებასა და მასზე მოდებული ძალების მიერ შესრულებულ მუშაობას შორის გარკვეული კავშირი არსებობს. ამ კავშირის დადგენა ყველაზე იოლად მუდმივი \(\vec{F}\) ძალის მოქმედებით წრფეზე მოძრავი სხეულის განხილვითაა შესაძლებელი. ამ შემთხვევაში ძალის ვექტორი \(\vec{F},\) გადაადგილება \(\vec{s},\) სიჩქარე \(\vec{v},\) და აჩქარება \(\vec{a},\) წრფის გასწვრივაა მიმართული და სხეული თანაბარ აჩქარებულ მოძრაობას ასრულებს. თუ საკოორდინატო ღერძს მოძრაობის წრფის გასწვრივ მივმართავთ, \(F\), \(s\), \(v\) და \(a\) შეიძლება, ალგებრულ სიდიდეებად განვიხილით (დადებითი ან უარყოფითი შესაბამისი ვექტორის მიმართულებიდან გამომდინარე). ძალის ეს მუშაობა შეიძლება ასე ჩაიწეროს \(A=Fs\). თანაბარაჩქარებული მოძრაობის გადაადგილება \(s\) გამოისახება ფორმულით
\(s=\frac{v_{2}^{2}-v_{1}^{2}}{2a}\).
აქედან გამომდინარეობს, რომ
\(A=Fs=ma\frac{v_{2}^{2}-v_{1}^{2}}{2a}=\frac{mv_{2}^{2}}{2}-\frac{mv_{1}^{2}}{2}.\)
ეს გამოსახულება უჩვენებს, რომ ძალის (ან ძალების ტოლქმედის) მიერ შესრულებული მუშაობა დაკავშირებულია სიჩქარის კვადრატის ცვლილებასთან (და არა თვით სიჩქარესთან).
ფიზიკური სიდიდეს, რომელიც სხეულის მასის მისი სიჩქარის კვარატზე ნამრავლის ნახევრის ტოლია სხეულის კინეტიკურ ენერგიას უწოდებენ:
\(E_{k}=\frac{mv^2}{2}.\)
სხეულზე მოდებული ძალის მიერ შესრულებული მუშაობა სხეულის კინეტიკური ენერგიის ცვლილების ტოლია.
\(A=E_{k2}-E_{k1}.\)
ამ მტკიცებულებას კინეტიკური ენერგიის თეორემას უწოდებენ. იგი სამართლიანია ზოგად შემთხვევაშიც, როცა სხეული მოძრაობს ისეთი ცვლადი ძალის მოქნედებით, რომლის მიმართულება არ ემთხვევა გადაადგილების მიმართულებას.
კინეტიკური ენერგია – მოძრაობის ენერგიაა. \(\vec{v}\) სიჩქარით მოძრავი \(m\) მასის სხეულის კინეტიკური ენერგია იმ მუშაობის ტოლია, რომელიც უნდა შეასრულოს უძრავ სხეულზე მოდებულმა ძალამ, სხეულისათვის ასეთი სიჩქარის მისანიჭებლად:
\(A=\frac{mv^{2}}{2}=E_{k}.\)
თუ სხეული \(\vec{v}\) სიჩქარით მოძრაობს, მაშინ მისი სრული გაჩერებისათვის საჭირო, შესრულებული მუშაობა ტოლია:
\(A=-\frac{mv^{2}}{2}=-E_{k}.\)
ფიზიკაში კინეტიკურ ანუ მოძრაობის ენერგიასთან ერთად მნიშვნელოვან როლს ასრულებს პოტენციური ენერგიის ან ურთიერთქმედების ენერგიის ცნება.
პოტენციური ენერგია სხეულების ურთუერთგანლაგებით განისაზღვრება (მაგალითად, სხეულის მდებარეობით დედამიწის ზედაპირის მიმართ). პოტენციური ენერგიის ცნება მხოლოდ იმ ძალებისათვის შეიძლება იყოს შემოტანილი, რომელთა მიერ შესრულებული მუშაობა ტრაექტორიაზე არ არის დამოკიდებული და მხოლოდ სხეულის საწყისი და საბოლოო მდებარეობით განისაზღვრება. ასეთ ძალებს კონსერვატიულ ძალებს უწოდებენ.
კონსერვატიული ძალების მიერ ჩაკეტილ ტრაექტორიაზე შესრულებული მუშაობა ნულის ტოლია. ამ გამონათქვამს ხსნის ნახ. 2.

ნახ. 2. ჩაკეტილ ტრაექტორიაზე მოძრაობა
კონსერვატიული ძალის თვისებები აქვთ სიმძიმისა და დრეკადობის ძალებს. ამ ძალებისათვის შეიძლება პოტენციური ენერგიის ცნების შემოღება.

ნახ. 3. სიმძიმის ძალის მუშაობა
ეს მუშაობა ტოლია საწინააღმდეგო ნიშნით აღებული რაღაც \(mgh\) სიდიდისა. ამ ფიზიკურ სიდიდეს სიმძიმის ძალის ველში სხეულის პოტენციურ ენერგიას უწოდებენ
\(E_{p}=mgh\).
იგი ტოლია იმ მუშაობისა რომელსაც სიმძიმის ძალა ნულოვან დონეზე დაშვების დროს ასრულებს.
სიმძიმის ძალის მუშაობა სხეულის, საწინააღმდეგო ნიშნით აღებული, პოტენციური ენერგიის ტოლია .
\(A=-(E_{p2}-E_{p1})\).
პოტენციური ენერგია Eр დამოკიდებულია ნულოვანი დონიდად რა სიმაღლეზეა სხეული, ე.ი. \(OY\) ღერძის კოორდინათთა სათავის არჩევაზე. ფიზიკური არსი აქვს არა თვით პოტენციურ ენეგიას, არამედ მის ცვლილებას სხეულის ერთი მდებარეობიდან მეორეში გადანაცვლებისას \(\Delta E_{p}=E_{p2}-E_{p1}\). ცვლილება ნულოვანი დონის არჩევაზე არაა დამოკიდებული.
თუ ვიხილავთ სხეულის მოძრაობას დედამიწის მიზიდულობის ველში, ზედაპირიდან მნიშვნელოვან მანძილებზე, მაშინ პოტენციური ენერგიის განსაზღვისათვის მხედველობაში უნდა იქნეს მიღებილი სიმძიმის ძალის დამოკიდებულება დედამიწის ცენტრიდან დაშორებაზე (მსოფლიო მიზიდულობის კანონი). მსოფლიო მიზიდულობის ძალებისათვის პოტენციური ენერგია უმჯობესია ავითვალოთ უსასრულოდ დაშორებული წერთილიდან, ე.ი. უსასრულოდ დაშორებული წერტილში პოტენციური ენერგია ჩავთვალოთ ნულის ტოლად. დედამიწის ცენტრიდან \(r\) მანძილზე დაშორებული \(m\) მასის სხეულის პოტენციური ენერგია გამოისახება ფორმულით (პარაგრაფი 1,24):
\(E_{p}=-G\frac{Mm}{r},\)
სადაც \(M\)– დედამიწის მასაა, \(G\)– გრავიტაციული მუდმივა.
პოტენციური ენერგიის ცნების შემოღება შესაძლებელია დრეკადობის ძალისთვისაც. ამ ძალასაც აქვს კონსერვატულობის თვისება. ზამბარის გაჭიმვა (ან შეკუმშვა) შესაძლებელია სხვადასხვა გზით.
შეიძლება ზამბა უბრალოდ წავაგრძელოდ რაღაც \(x\) სიდიდით, ან ჯერ წავაგრძელოთ \(2x\) სიდიდით და მერე შევკუმსოთ \(x\) მნიშვნელობამდე და ა.შ. ყველა შემთხვევაში დრეკადობის ძალა ასრულებს ერთიდაიგივე მუშაობას, რომელიც მხოლოდ ზამბარის საბოლოო \(x\) წაგრძელებაზეა დამოკიდებული. ეს მუშაობა ზამბარის დეფორმაციის გამომწვევი გარე ძალის მიერ შესრულებული მუშაობის ტოლია, ოღონდ საწინააღმდეგო ნიშნით:
\(A_{dach}=-A=-\frac{kx^{2}}{2},\)
სადაც \(k\)– ზამბარის სიხისტეა. დაჭიმულ (ან შეკუმშულ) ზამბარას შეუძლია მასზე მიმაგრებული სხეული მოიყვანოს მოძრაობაში, ე.ი. სხეულს კინეტიკური ენერგია მიანიჭოს. აქედან გამომდინარე, ასეთ ზამბარას აქვს ენერგიის მარაგი. ზამბარის ( ნებისმიერი სხვა დეფორმირებული სხეულის) პოტენციური ენერგიას უწოდებენ სიდიდეს
\(E_{p}=\frac{kx^{2}}{2}.\)
დრეკადი, დეფორმირებული სხეულის პოტენციური ენერგია ტოლია მუშაობისა, რომელიც სრულდება მოცემული მდგომარეობიდან ნულოვანი დეფორმაციის მდომარეობაში გადასვლისას.
თუ ზამბარა საწყის მდებარეობაში უკვე დეფორმირებილი იყო და მისი წაგრძელება ტოლი იყო \(x_{1}\)–სა, მაშინ ახალი \(x_{2}\) წაგრძელების მდგომარეობაში გადასვლისას დრეკადობის ძალა ასრულებს საწიმააღმდეგო ნიშნით აღებული პოტენციური ენერგიის ცვლილების ტოლ მუშაობას:
\(A_{dach}=-(E_{p2}-E_{p1})=-\left (\frac{kx_{2}^{2}}{2}-\frac{kx_{1}^{2}}{2} \right ).\)
დრეკადი დეფორმაციის პოტენციური ენერგია – სხეულის ცალკეულ ნაწილებს შორის დრეკადობის ძალების საშუალებით ურთიერთქმედების ენერგიაა.
კონსერვატულობის თვისებით, სიმძიმისა და დრეკადობის ძალების გარდა, ზოგიერთი სხვა ძალაც ხასიათდება, მაგალითად, დამუხტულ ნაწილაკებს შორის ელექტროსტატიკური ურთიერთქმედების ძალა. ხახუნის ძალას ეს თვისება არ გააჩნია. ხახუნის ძალის მუშაობა გავლილ მანძილზეა დამოკიდებული. პოტენციური ენერგიის ცნების შემორება ხახუნის ძალისთვის არ შეიძლება.

{loadnavigation}
მოძრაობის ენერგეტიკული მახასიათებლები ემყარება მექანიკური მუშაობის ანუ ძალის მუშაობის ცნებას.
მუდმივი \(\vec{F}\) ძალის მიერ შესრულებული მუსაობა A, ეწოდება ფიზიკურ სიდიდეს, რომელიც ძალის, გადაადგილების მოდულების და \(\vec{F}\) ძალის და \(\vec{S}\) გადაადგილების ვექტორებს შორის მდებარე კუთხის კოსინუსის ნამრავლის ტოლია (ნახ. 1):
\(A=FS\cos \alpha\).
მუშაობა სკალარული სიდიდეა. ის შეიძლება, როგორც დადებითი \((0^{\circ}<\alpha \leq 90^{\circ})\), ასევე უაროფითი \((90^{\circ}<\alpha \leq 180^{\circ})\) იყოს. როცა \(\alpha =90^{\circ}\), ძალის მიერ შესრულებული მუშაობა ნულის ტოლია. \(Si\) სისტემაში მუშაობა ჯოულებში (ჯ) იზომება.
1 ჯოული 1 ნ ძალის მიერ, ძალის მოქმედების გასწვრივ, 1 მ–ზე გადაადგილებისას შესრულებილი მუშაობაა.
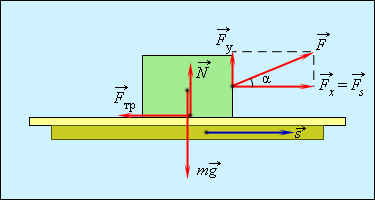
ნახ. 1.
\(\vec{F}\) ძალის მუშაობა: \(A=Fs\cos \alpha =F_{s}s\)
\(\vec{F}\) ძალის \(\vec{s}\) გადაადგილებაზე გეგმილი \(\vec{F}_{s}\) მუდმივი რჩება, მუშაობა მცირე \(\Delta s_{i}\) გადაადგილებებისათვის უნდა გამოითვალოს და შედეგები აიჯამოს:
\(A=\sum \Delta A_{i}=\sum F_{si}\Delta s_{i}\).
როცა \((\Delta s_{i}\rightarrow 0)\), ეს ჯამი გადადის ინტეგრალში.
მუშაობა გრაფიკულად გამოისახება \(F_{s}(x)\) გრაფიკის მრუდწირული ფიგურასა და \(OX\) ღერძს შორის მოქცეული ფართობით (ნახ. 2).
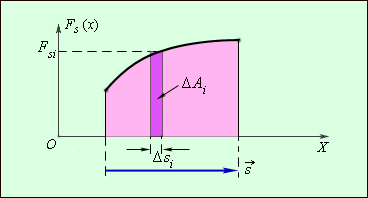
ნახ. 2.
მუშაობის გრაფიკულო გამოისახვა. \(\Delta A_{i}=F_{si}\Delta s_{i}\)
ისეთი ძალის მაგალითად, რომლის მოდულიც კოორდინატზეა დამოკიდებული, შეძლება ზამბარის დაჭიმულობის ძალა განვიხილოთ. ეს ძალა ჰუკის კანონს ემორჩილება. ზამბარის გასაჭიმად მას უნდა. მოდულით ზამბარის წაგრძელიბის პროპორციალი \(\vec{F}\) ძალა მოვდოთ (ნახ. 3).
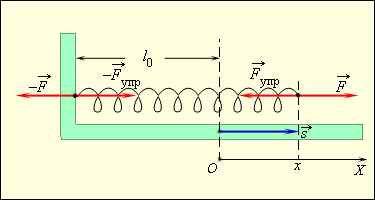
ნახ. 3.
ზამბარის გაჭიმვა. გარე \(\vec{F}\) ძალის მიმართულიბა ემთხვევა გადაადგილების მიმართულებას \(\vec{s}\cdot F_{s}=kx,\) \(k\) – ზამბარის სიხისტეა. \(\vec{F}_{dach}=-\vec{F}\)
გარე ძალის მოდულის \(x\)ღერძისადმი დამოკიდებულება გარაფიკზე წრფითაა გამოსახული (ნახ. 4).
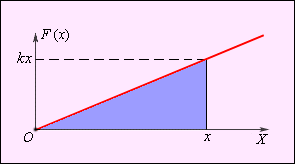
ნახ. 4.
გარე ძალის მოდულის x ღერძისადმი დამოკიდებულება ზამბარის დაჭიმვის დროს
ნახ. 4–ზე სამკუთხედის ფართობიდან შეიძლება განისაზღვროს მუშაობა, რომელსაც ზამბარის მარჯვენა, თავისუფალ მხარეს მოდებული გარე ძალა ასრულებს:
\(A=\frac{kx^{2}}{2}\)
ამავე ფორმულით გამოისახება ზამბარის შეკუმშვისას შესრულებული მუშაობა. ორივე შემთხვევაში დრეკადობის ძალის \(\vec{F}_{dach}\) მიერ შესრულებული მუშაობა მოდულით ტოლია გარე \(\vec{F}\) ძალის მიერ შესრულებული მუშაობისა და საწინააღმდეგო ნიშანი აქვს.
თუ სხეულზე რამოდენიმე ძალაა მოდებული, ყველა ძალის სრული მუშაობა ტოლია თითოეული ძალის მიერ შესრულებული მუშაობების ალგებრული ჯამისა. გადატანითი მოძრაობისას, როცა ყველა ძალის მოდების წერტილები ერთიდაიგივე გადაადგილებას ასრულებს, ყველა ძალის სრული მუშაობა ტოლია მოდებული ძალების ტოლქმედი მუშაობისა. დროის ერთეულში ძალის მიერ შესრულებულ მუშაობას სიმძლავრე ეწოდება. \(N\) სიმძლავრე ფიზიკური სიდიდეა, რომელიც \(A\) მუშაობის იმ \(t\) დროსთან ფარდობის ტოლია, რომლის განმავლობაშიც შესრულდა ეს მუშაობა:
\(N=\frac{A}{t}.\)
საერთაშორისო სისტემაში (\(Si\)) სიმძლავრის ერთეულს ვატი (ვტ) ეწოდება. ვატი ისეთი ძალის სიმძლავრის ტოლია, რომელიც 1 წამის განმავლობაში 1 ჯოულ მუშაობას ასრულებს.
1ვტ=1ჯ/1წმ.
