{loadnavigation}
სხეულების ურთიერთქმედებისას ერთი სხეულის იმპულსი შეიძლება, ნაწილობრივ ან სრულად, გადაეცეს მეორე სხეულს. თუ სხეულიბის სისტემაზე სხვა სხეულიბის მხრიდან გარე ძალები არ მოქმედებენ, მაშინ ასეთ სისტემას ჩაკეტილი სისტემა ეწოდება.
ჩაკეტილ სისტემაში, მასში შემავალი ყველა სხეულის იმპულსების ვექტორული ჯამი, ამ სისტემის სხეულების ნებისმიერი ურთიერთქმედებისას, უცვლელი რჩება.
ბუნების ამ ფუნდამენტალურ კანონს იმპულსის მუდმივობის (შენახვის) კანონს უწოდებენ. ის ნიუტონის მეორე და მესამე კანონების შედეგს წარმოადგენს.
განვიხილოთ ჩაკეტილ სისტემაში შემავალი რაიმე ორი სხეული. ამ სხეულიბის ურთიერთქმედების ძალები აღვნიშნით \(\vec{F_{1}}\) და \(\vec{F_{2}}\) ნიუტონის მესამე კანონის თანახმად \(\vec{F_{2}}=-\vec{F_{1}}\) თუ ეს სხეულები \(t\) დროის განმავლობაში ურთიერთქმედებენ, მაშინ ურთიერთქმედების ძალების იმპულსები მოდულით ტოლია და საპირისპიროდაა მიმართული: \(\vec{F_{2}}t=-\vec{F_{1}}t.\) ამ სხეულიბის მიმართ გამოვიყენოთ ნიოტონის მეორე კანონი:
\(\vec{F_{1}}t=m_{1}\vec{v_{1}^{'}}-m_{2}\vec{v_1}; \vec{F_{2}}t=m_{1}\vec{v_{2}^{'}}-m_{2}\vec{v_{2}};\)
ეს ტოლობა ნიშნავს, რომ ორი სხეულის ურთიერთქმედების შედეგად მათი ჯამური იმპულსი არ იცვლება. ჩაკეტილ სისტემაში სხეულთა წყვილის ნებისმიერი სახის ურთიერთქმედების განხილვიდან შეიძლება გავაკეთოდ დასკვნა, რომ ჩაკეტილ სისტემის შინაგან ძალებს არ შეუძლიათ ჯამური იმპულსის, ე.ი. სისტემაში შემავალი ყველა სხეულის იმპულსების ვექტორული ჯამის შეცვალა.
ნახ. 1–ზე ორი სხვადასხვა მასის ბურთის, რომელთაგან ერთი დაჯახებამდე უძრავი იყო, არაცენტრალური შეჯახებისას იმპულსის შენახვის კანონია ნაჩვენები.
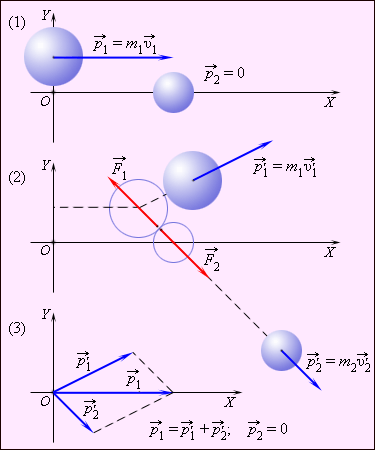
ნახ. 1.
სხვადასხვა მასის ბურთების არაცენტრალური შეჯახებისას.:1 – იმპულსები შეჯახებამდე; 2 - იმპულსები შეჯახების შემდეგ; 3 - იმპულსების დიაგრამა
ნახ. 1–ზე გამოსახილია ბურთების იმპულსის ვექტორები დაჯახებამდე და დაჯახების შემდეგ, დავაგეგმილოთ \(OX\) და \(OY\) ღერძებზე. იმპულსის შენახვის კანონი სამართლიანია ვექტორების ღერძებზე გეგმილებისთვისაც, კერძოდ, იმპულსების ამ დიაგრამიდან გამომდინარეობს, რომ დაჯახების შემდეგ ორივე ბურთის \(\vec{P_{1}^{'}}\) და \(\vec{P_{2}^{'}}\) იმპულსების ვექტორების გეგმილები %OY%ღერძზე მოდულით ტოლი უნდა იყოს და ჰქონდეთ სხვადასხვა ნიშანი, რომ მათი ჯამი ნულის ტოლი გამოვიდეს.
იმპულსის შენახვის კანონი ბევრ შემთხვევაში ურთიერთმოქმედი სხეულიბის სიჩქარეების პოვნის საშუალებას იძლევა, მაშინაც კი როცა მომქმედი ძალების სიდიდეები ცნობილი არ არის. ამის მაგალითად რეაქტიული მოძრაობა გამოდგება.
ქვემეხიდან გასროლის დროს ადგილი აქვს უკუგებას – ჭურვი მოძრაობს წინ, ქვემეხი კი უკან დაგორდება. ჭურვი და ქვემეხი – ურთიერთმოქმედი სხეულიბია. უკუგდებისას ქვემეხის მიერ მიღებული სიჩქარე დამოკიდებულია, მხოლოდ ჭურვის სიჩქარესა და მასების ფარდობაზე (ნახ. 2). თუ ქვემეხისა და ჭურვის სიჩქარეებს აღვნიშნავთ \(\vec{V}\) და \(\vec{v}\) ხოლო მასებს \(M\) და \(m\)–ით, მაშინ იმპულსის შენახვის კანონის საფუძველზე შეიძლება დაიწეროს \(OX\) ღერძზე გეგმილებისათვის
\(MV+mv=0; V=-\frac{m}{M}v.\)

ნახ.2.
უკუგება ქვემეხიდან გასროლისას

უკუგების პრინციპზეა დამყარებული რეაქტიული მოძრაობა. კოსმოსურ ხომალდში საწვავის წვისას, მაღალ ტემპერატურამდე გახურებული აირი დიდი \(\vec{u}\) სიჩქარეით გამოიტყორცნება ხომალდის კუდიდან. გამოტყორცნილი აირის მასა \(m\)–ით აღვნიშნოთ, ხოლო რაკეტის მასა აირის გამოსვლის შემდეგ \(M\)–ით. „ხომალდი–აირი“ ჩაკეტილი სისტემისათვის იმპულსის შენახვის კანონის საფუძველზე (ქვემეხიდან გასროლის ამოცანის ანალოგიურად) შეიძლება დაიწეროს:
\(V=-\frac{m}{M}u.\)
სადაც \(V\)– რაკეტის სიჩქარეა აირის გამოდინების შემდეგ. მოცემულ მომენტში იგულისხმება რომ, ხომალდის საწყისი სიჩქარე ნულის ტოლია my site.
ხომალდის სიჩქარისათვის მიღებული ფორმულა სამართლიანია მხოლოდ იმ სემთხვევაში, თუ დამწვარი (გადამუშავებული) აირი ხომალდიდან ერთდროულად გამოიტყოცვება. სინამდვილეში გამოდინება ხდება თანდათან, ხომალდის მთელი, აჩქარებული მოძრაობის პერიოდში. აირის ყოველი მომდევნო პორცია გამოიტყოცნება ხომალდიდან, რომელმაც უკვე შეიძინა რაღაც სიჩქარე.
ზუსტი ფორმულის მისაღებად აირის გამოდინების პროცესი უფრო დეტელურად უნდა იქნეს განხილული. ვთქვათ ხომალდს დროის \(t\) მომენტში \(M\) მასა აქვს და მოძრაობს \(\vec{v}\) სიჩქარით (ნახ. 3 (1)). დროის მცირე \(\Delta t\) ინტერვალში გამოედინება აირის რაღაც პორცია ფარდობითი სიჩქარით \(\vec{u}.\) ხომალდს \(t+\Delta t\) მომენტში ექნება სიჩქარე \(\vec{v}+\Delta \vec{v},\) ხოლო მასა გახდება ტოლი \(M+\Delta M\), სადაც \(\Delta M<0\) (ნახ. 3 (2)). ნათელია, რომ გამოტყორცნილი აირის მასა ტოლია \(-\Delta M>0\). აირის სიჩქარე \(OX\) ინერციულ სისტემაში იქნება ტოლი \(\vec{v}+\vec{u}.\) გამოვიყენოთ იმპულსის შენახვის კანონი. დროის \(t+\Delta t\) მომენტში ხომალდის იმპულსი ტოლია \((M+\Delta M)(\vec{v}+\Delta \vec{v}),\) ხოლო გამოტყორცნილი აირის იმპულსი კი \((-\Delta M)(\vec{v}+\vec{u}).\) დროის \(t\) მომენტში მთელი სისტემის იმპულსი ტოლია \(M\vec{v}.\) ვგულისხმობთ რა, რომ სისტემა „ხომალდი–აირი“ ჩაკეტილია შეიძლება დაიწეროს:
\(M\vec{v}=(M+\Delta M)(\vec{v}+\Delta \vec{v})-\Delta M(\vec{v}+\vec{u})\) ან \(M\Delta \vec{v}=\Delta M\vec{u}-\Delta M\Delta \vec{v}\)
\(\Delta M\Delta \vec{v}\) სიდიდის უგულვებესყოფა შეიძლება, რადგან \(|\Delta M|<<M\). ტოლობის ორივე მხარის \(\Delta t\)–ზე გაყოფით და \(\Delta t\rightarrow 0\) ზღვარზე გადასვლით, მივიღებთ
\(M\frac{\Delta \vec{v}}{\Delta t}=\frac{\Delta M}{\Delta t}\vec{u}\, \; (\Delta t\rightarrow 0)\) ან \(M\vec{a}=-\mu \vec{u}.\)

ნახ. 3.
ხომალდი მოძრაობს თავისუფალ სივრცეში (გრავიტაციის გარეშე). 1 – დროის \(t\) მომენტში. ხომალდის მასა \(M\), მისი სიჩქარე \(\vec{v}\).2 – ხომალდი\(t+\Delta t\) მომენტში. ხომალდის მასა \(M+\Delta M\), სადაც \(\Delta M<0\), მისი სიჩქარე \(\vec{v}+\Delta \vec{v},\) გამოტყორცნილი აირის მასა \(-\Delta M>0\), აირის ფარდიბითი სიჩქარე \(\vec{u},\) აირის სიჩქარე ინერციულ სისტემაში \(\vec{v}+\vec{u}\)

\(\mu =-\frac{\Delta M}{\Delta t}\; (\Delta t\rightarrow 0)\) სიდიდე საწვავის ხარჯია დროის ერთეულში. \(-\mu \vec{u}\) სიდიდეს წევის რეაქტიულ ძალას უწოდებენ – \(\vec{F_{p}}.\) წევის რეაქტიულ ძალა ხომალდზე აირის გამოდინების მხრიდან მოქმედებს, იგი მიმართულია ფარდობითი სიჩქარის საპირისპიროდ. დამოკიდებულება
\(M\vec{a}=\vec{F_{p}}=-\mu \vec{u},\)
გამოსახავს ნიუტონის მეორე კანონს ცვლადი მასის მქონე სხულისათვის. თუ აირი ხომალდის კუდიდან მკაცრად უკან გაიტყოცნება (ნახ. 3), მაშინ სკალარული სახით იგი ჩაიწერება:
\(Ma=\mu u\),
სადაც \(u\)– ფარდობითი სიჩქარის მოდულია. ამ ფორმულის ინტეგრირების საშუალებით შეიძლება ხომალდის საბოლოო \(v\) სიჩქარის გამოსათვლელი ფორმულის მიღება:
\(v=u\: \: ln\left (\frac{M_{0}}{M} \right )\)
სადაც \(\frac{M_{0}}{M}\) – ხომალდის საწყისი და საბოლოო სიჩქარეების ფარდობაა. ამ ფორმულის მიხედვით, შეიძლება ხომალდის სიჩქარე აღემატებოდეს აირის გამოდინების სიჩქარეს. აქედან გამომდინარეობს, რომ ხომალდს შეიძლება ჰქონდეს კოსმოსური ფრენისთვის აუცილებელი დიდი სიჩქარე. მაგრამ, ეს მიიღწევა საწვავის მნიშვნელოვანი რაოდენობის დანახარჯით, რაც ხომალდის მასის დიდ ნაწილს შეადგენს. მაგალითად, პირველი კოსმოსური სიჩქარის \(u=v_{1}=7,9\cdot 10^{3}\) მ/წმ მისაღწევად როცა \(u=3\cdot 10^{3}\) მ/წმ (აირის გამოდინების სიჩქარე საწვავის წვისას 2-4 კმ/წმ რიგისაა) ერთსაფეხურიანი ხომალდის სასტარტო მასა დაახლოებით 14–ჯერ უნდა აღემატებოდეს საბოლოო მასას. \(v=4u\) საბოლოო სიჩქარის მისაღწევად \(\frac{M_{0}}{M}\) ფარდობა უნდა იყოს 50–ის ტოლი.
სასტარტო მასის მნიშვნელოვანი შემცირება მიიღწევა მარვალსაფეხურიანი ხომალდის გამოყენებისას, როცა ხომალდს საფეხურები სცილდება საწვავის გამოლევის შემდეგ. შემდგომი გაქანების (სიჩქარის ზრდის) პროცესიდან გამოირიცხება საწვავის კონტეინერის მასა.
{loadnavigation}
ვთქვათ \(m\) მასის სხეულზე რაღაც მცირე \(\Delta t\) დროის განმავლიბაში მოქმედებს ძალა \(\vec F\). ამ ძალის მოქმედებით სხეულის სიჩქარე იცვლება \(\Delta \vec{v}=\vec{v_{2}}-\vec{v_{1}}\). აქედან გამომდინარე,\(\Delta t\) დროის განმავლობაში სხეული მოძრაობს აჩქარებით
\(\vec{a}=\frac{\Delta \vec{v}}{\Delta t}=\frac{\vec{v_{2}}-\vec{v_{1}}}{\Delta t}\)
დინამიკის ძირითადი კანონიდან (ნიუტონის მეორე კანონი) გამომდინარეობს:
\(\vec{F}=m\vec{a}=m\frac{(\vec{v_{2}}-\vec{v_{1}})}{\Delta t}\) ან \(\vec{F}\Delta t=m\vec{v_{2}}-m\vec{v_{1}}=m\Delta \vec{v}=\Delta (m\vec{v}).\)
ფიზიკურ სიდიდეს, რომელიც სხეულის მასისა და მისი სიჩქარის ნამრავლის ტოლია, სხეულის უმპულსი (ან სხეულის მოძრაობის რაოდენობა) ეწოდება. სხეულის იმპულსი ვექტორული სიდიდეა. იმპულსის ერთეული \(Si\) სისტემაშიკოლოგრამ–მეტრია წამში (კმ.მ/წმ).
ახალი ტერმინების გამოყენებით ნიუტონის მეორე კანონი შეიძლება ასე ჩამოვაყალიბით: სხეულის იმპულსის (მოძრაობის რაოდენობის) ცვლილება ძალის იმპულსის ტოლია. ძალის იმპულსი აღვნიშნოთ \(\vec{P}\)–თი და მეორე კანონი შეიძლება ასე ჩაიწეროს:
\(\vec{F}\Delta t=\Delta \vec{P}.\)
სწორედ ასეთი ზოგადი სახით ჩამოაყალიბა იგი ნიუტონმა. ამ გამოსახულებაში \(\vec{F}\) ძალა სხეულზე მოდებული ყველა ძალების ტოლქმედს წარმოადგენს. ეს ვექტორული ტოლობა შეიძლება კოორდინათტა ღერძებზე გეგმილებით ასე ჩაიწეროს:
\(F_{x}\Delta t=\Delta P_{x}; F_{y}\Delta t=\Delta P_{y}; F_{z}\Delta t=\Delta P_{z}.\)
ამგვარად, ნებისმიერი ურთიერთმართობულ ღერძზე სხეული იმპულსის გეგმილის ცვლილება იმავე ღერძზე ძალის იმპულსის გეგმილის ტოლია. მაგალითისთვის განვიხილოთ ერთგანზომილებიანი მოძრაობა, ე.ი. სხეულის მოძრაობა ერთ–ერთ საკოორდინატო ღერძზე (მაგ. \(OY\)–ზე). ვთქვათ სხეული სიმძიმის ძალის მოქმედებით თავისუფლად ვარდება საწყისი \(v_{0}\) სიჩქარით; ვარდნის დრო \(t\)–ა. \(OY\) ვერტიკალურად ქვევით მივმართოდ. \(t\) დროის განმავლობაში სიმძიმის ძალის იმპულსი \(mgt\)–ს ტოლია. ეს იმპულსი სხეულის იმპულსის ცვლილების ტოლია
\(mgt=\Delta P=m(v-v_{0})\), სადაც \(v=v_{0}+gt.\)
ეს უბრალო შედეგი ემთხვევა თანაბარაჩქარებული მოძრაობის კინემატიკურ ფორმულას. ამ მაგალითში ძალა \(t\) დროის ინტერვალში მოდულით უცვლრლი რჩება. ძალის სიდიდე თუ იცვლება, გამოსახულებაში \(t\) დროის ინტერვალში საშუალო ძალის მნიშვნელობა Fსაშ. უნდა ჩაისვას. ნახ. 1 ნაჩვენებია დროზე დამოკიდებული ძალის იმპულსის განსაზღვრის მეთოდი.
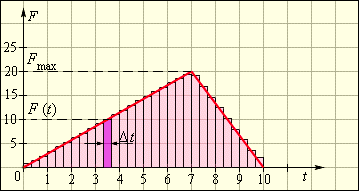
ნახ. 1.
\(F(t)\) დამოკიდებულების გრაფიკიდან ძალის იმპულსის განსაზღვრა.
დროის ღერძზე გამოვყოთ Δt მცირე ინტერვალი, რომელშიც ძალა \(F(t)\) პრაქტიკულად არ იცვლება. ძალის იმპულსი \(F(t)\Delta t\)- \(\Delta t\) დროის განმავლობაში დაშტრიხული სვეტის ფართობის ტოლია. თუ დროის მთელ ღერძს 0 –დან \(t\)–მდე დავყოფთ \(\Delta t_{i}\) მცირე ინტერვალებად, და შემდეგ კი ავჯამავთ ძალის იმპულსებს ყველა \(\Delta t_{i}\) მონაკვეტში, მაშინ ჯამური ძალის იმპული ამ კიბისებური მრუდის მიერ დროის ღერძთან წარმომნილი ფართობის ტოლი გამოვა. როცა \((\Delta t_{i}\rightarrow 0)\), მოვიღებთ \(F(t)\) გრაფიკის მიერ დროის ღერძთან შედგენილ ფართობს. \(F(t)\) გრაფიკის მიხედვით ძალის იმპულსის განსაზღვრის ეს მეთოდი ზოგადია და ძალის დროში ცვლილების ნებისმიერი კანონისათვის გამოიყენება. მათემატიკური ამოცანა დაიყვანება \(F(t)\)–ს \([0;t]\) ინტერვალში ინტეგრირებაზე. ნახ. 1–ზე მოცემული ძალის იმპულსი \(t_{1}=0\)–დან \(t_{2}=10\)–მდე უდრის:
Fსაშ.\((t_{2}-t_{1})=\frac{1}{2}F_{max}(t_{2}-t_{1})=100\)ნ.წმ=100კგ.მ/წმ
Fსაშ \(=\frac{1}{2}F_{max}=10\)ნ
ზოგიერთ შემთხვევაში, საშუალო ძალა Fსაშ შეიძლება განისაზღვროს თუ ცნობილია მისი მოქმედების დრო და სხეულისადმი მინიჭებული იმპულსი. მაგალითად, ფეხბურთელი 0,415 კგ ბურთზე ძლირი დარტყმით, მას ანიჭებს υ = 30 მ/წმ სიჩქარეს. დარტყმის ხანგრძლივობა დაახლოებით 8·10–3 წმ–ია.
დარტყმის შედეგად ბურთის მიერ შეძენილი \(P\) იმპულსი ტოლია:
\(P=mv=12,5\)კგ.მ/წმ.
აქედან გამომდინარე, საშუალო ძალა Fსაშ, როლითაც დარტყმის პერიოდში ფეხბურთელი მოქმედებს ბურთზე, ტოლია:
Fსაშ \(=\frac{P}{\Delta T}=1,56\cdot 10^{3}\)ნ
ეს ძალიან დიდი ძალაა. ის დაახლოებით 160 კგ მასის წონის ტოლია.
თუ სხეული ძალის მოქმედების პერიოდში რაღაც მრუდწირულ ტრაექტორიაზე მოძრაობს, მაშინ სხეულის საწყისი \(\vec{P_{1}}\) და საბოლოო \(\vec{P_{2}}\) იმპულსები შეიძლება განსხვავდებოდეს როგორც მოდულით, ასევე მიმართულებითაც. ამ შემთხვევაში იმპულსის ცვლილების \(\Delta \vec{P}\) განსაზღვრისათვის ხელსაყრელია იმპულსების დიაგრამას გამოყენება, რომელზეც გამოსახულია პარალელოგრამის წესით აგებული \(\vec{P_{1}}\) და \(\vec{P_{2}}\) ვექტორები და ასევე ვექტორი \(\Delta \vec{P}=\vec{P_{2}}-\vec{P_{1}}\). ნახ. 2–ზე გამოსახულია იმპულსების დიაგრამა უსწორმასწორო კედლიდან არეკვლილი ბურთისათვის. \(m\) მასის ბირთი დაეჯახა კედელს \(\vec{v_{1}}\) სიჩქარით ნორმალისადმი (ღერძი \(OX\)) \(\alpha\) კუთხით, გადაიხარა ნორმალიდან \(\beta\) კუთხით და გააგრძელა გზა \(\vec{v_{2}}\) სიჩქარით. ბურთის კედელთან კონტაქტის დროს მასზე მოქმედებდა რაღაც \(\vec{F}\) ძალა, რომლის მიმართულება ემთხვევა \(\Delta \vec{P}\) ვექტორს.
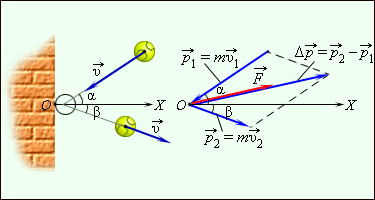
ნახ. 2.
უსწორმასწორო კედლიდან ბურთის არეკვლა და იმპულსების დიაგრამა
დრეკად კედელზე \(m\) მასის ბურთს ნორმალური (პირდაპირი) \(\vec{v_{1}}=\vec{v}\) სიჩქარით შეჯახებისას, არეკვლის შემდეგ აქვს \(\vec{v_{2}}=-\vec{v}\) სიჩქარე. აქედან გამომდინარეობს, რომ არეკვლისას იმპულსის ცვლილება ტოლია \(\Delta \vec{P}=-2m\vec{v}.\) \(OX\) ღერძზე დაგეგმილების შედეგი შეიძლება ჩაიწეროს სკალარული ფორმით Δpx = –2mυx. OX ღერძი მიმართულია კედლისაკენ, ამიტომ \(v_{x}<0\) და \(\Delta p_{x}>0\). აქედან გამომდინარე, იმპულსის ცვლილების მოდული \(\Delta P\) \(v\) \(v\) ბურთის სიჩქარიეს υ მოდულთან დაკავშირებულია ტოლობით \(\Delta P=2mv\).
{loadnavigation}
სითხის ძირითადი განსხვავება მყარი (დრეკადი) სხეულიბისაგან, მის მიერ ფორმის ადვილად შეცვლის უნარია (სითხე ვერ ინარჩულებს ფორმას). სითხის ნაწილებს შეუძლიათ თავისუფლად იმოძრაონ, ისრიალონ ერთმანეთის მიმართ. ამიტომაც სითხე ღებულობს იმ ჭურჭლის ფორმას, რომელშიაც ისაა ჩასხმული. სითხეში, ისევე როგორც აირის გარემოში, შეიძლება ჩავძიროთ მყარი სხეული. აირისაგან განსხვავებით სითხეები პრაქტიკულად არ იკუმშებიან.
სითხეში ჩაძირულ სხეულზე მოქმედებენ ძალები, რომლების სხეულის ზედაპირზე არიან განაწილებული. ასე განაწილებილი ძალების აღწერისათვის შემოყვანილია ახალი ფიზიკური სიდიდე – წნევა.
წნევა განისაზღვრება როგოც, ზედაპირის მართობულად მომქმედი ძალის 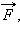 მოდულის ფარდობა ამ ზედაპირის ფართობთან S :
მოდულის ფარდობა ამ ზედაპირის ფართობთან S :
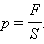
SI სისტემაში წნევა იზომება პასკალებში (პა):
1 პა = 1 ნ/მ2.
ხშირად გამოიყენება სისტემის გარეშე ერთეულები: ნორმალური ატმოსფერული წნევა (ატმ) და ვერცხლისწყლის სვეტის მილიმეტრი (მმHg):
1 ატმ=101325 პა=760 მმHg
ფრანგმა მეცნიერმა ბ.პასკალმა, XVII საუკუნეში, ემპირიულად დაადგინა კანონი, რომელსაც პასკალის კანონი ეწოდება:
სითხესა და აირში წნევა ყველა მიმართულების ერთნაირად გადაეცემა დ არ არის დამოკიდებული იმ ზედაპირის ორიენტაციაზე, რომელზეც ის მოქმედებს.
პასკალის კანონის საილუსტრაციოდ ნახ. 1–ზე სითხეში ჩაძირული პატარა მართკუთხა პრიზმაა გამოსახული. თუ დავუშვებთ, რომ პრიზმის მასალის სიმკვრივე სითხის სიმკვრივის ტოლია, მაშინ პრიზმა სითხეში განურჩეველი წონასწორობის მდგომარეობაში უნდა იმყოფებოდეს. ეს იმას ნიშნავს, რომ პრიზმის წახნაგებზე მომქმედი წნევის ძალები გაწონასწორებული უნდა იყვნენ. ეს მხოლოდ იმ შემთხვევაში მოხდება, თუ წნევა, ე.ი. ძალები, პრიზმის ყოველი წახნაგის ფართობის ერთეულზე, ერთნაირია: p1 = p2 = p3 = p.

ნახ. 1. პასკალის კანონი:p1 = p2 = p3 = p
წნევა სითხეში ჭურჭლის ფსკერზე და კედლებზე სითხის სვეტის სიმაღლეზეა დამოკიდებული.
სითხის წნევა, h სიმაღლისა და ფსკერის S ფართობის მქონე ცილინდრული ჭურჭლის ფსკერზე, სითხის mg სვეტის წონის ტოლია, სადაც m = ρghS – ჭურჭელში არსებული სითხის მასაა, ρ – სითხის სიმკვრივე. შესაბამისად
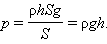
პასკალის კანონის მიხედვით სითხე h სიმაღლეზე ჭურჭლის გვერდით კიდლებზე ასეთივე წნევას ქმნის. სითხის ρgh სვეტის წნევას ჰიდროსტატიკურ წნევას უწოდებენ.
თუ სითხე იმყოფება დგუშიან ცილინდრში (ნახ. 2), მაშინ დგუშზე რაღაც გარე 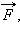 ძალით მოქმედებისას, სითხეში შეიძლება დამატებითი წნევა შეიქმნას p0 = F / S, სადაც S – დგუშის ფართობია.
ძალით მოქმედებისას, სითხეში შეიძლება დამატებითი წნევა შეიქმნას p0 = F / S, სადაც S – დგუშის ფართობია.
ამგვარად, სრული წნევა სითხეში h სიღრმეზე შეიძლება შემდეგი სახით ჩაიწეროს:
p = p0 + ρgh.
თუ ნახ. 2–ს დგუშს მოვაცილებთ, მაშინ სითხის ზედაპირზე წნევა ატმოსფერული წნევის ტოლი იქნება: p0 = pატმ.

ნახ. 2. წნევის დამოკიდებულიბა სითხის სვეტის სიმაღლეზე
სითხის სხვადასხვა დონეზე წნევების განსხვავების გამო აღიძვრება ამომგდები ანუ არქიმედეს ძალა 
ნახ. 2 ხსნის არქიმედეს ძალის მოქმედებას. სითხეში, h და S ფუძის ფართობის მქონე, მართკუთხა პარალელეპიპედის ფორმის სხეულია ჩაშვებული. ზედა და ქვედა წახნაგებზე წნევათა სხვაობა ტოლია:
Δp = p2 – p1 = ρgh
ამიტომაც ამომგდები ძალა 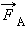 ზევითაა მიმართული და სიდიდით ტოლია
ზევითაა მიმართული და სიდიდით ტოლია
FА = F2 – F1 = SΔp = ρgSh = ρgV
სადაც V – სხეულის მიერ გამოდევნილი სითხის მიცულობაა, ხოლო ρV – მისი მასა.
სითხეში (ან აირში) ჩაშვებულ სხეულზე მომქმედი არქიმედეს ძალა სხეულის მიერ გამოდევნილი სითხის (ან აირის) წონის ტოლია. არქიმედეს კანონად წოდებული ეს მტკიცება ნებისმიერი ფორმის სხეულისათვისაა სამართლიანი.
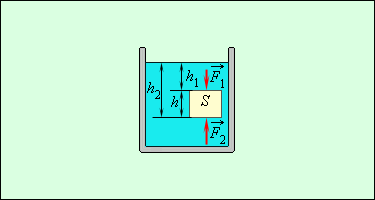
ნახ. 3.
არქიმედეს კანონი. FА = F2 – F1 = S(p2 – p1) = ρgSh, F1 = p1S,F2 = p2S
არქიმედას კანონიდან გამომდინარეობს, რომ თუ სხეულის საშუალო სიმკვრივე ρსხ სითხის (აირის) ρ სიმკვრივეზე მეტია, მაშინ სხეული ფსკერზე ჩაიძირება. თუ ρსხ< ρ, სხეული სითხის ზედაპირზე იცურებს. სხეულის სითხეში ჩაძირული ნაწილის მოცულობა იქნება ისეთი, რომ გამოდევნილი სითხის წონა ტოლი იქნება სხეულის წონისა. საჰაერო ბუშტის ჰაერში ასაფრენად მისი წონა ნაკლები უნდა იყოს გამოდევნილი ჰაერს წონისა. ამიტომაც, საჰაერო ბუშტებს მსუბუქი აირებით (წყალბადითა, ჰელიუმით) ან გამთბარი ჰაერით ბერავენ.
სითხეში სრული წნევის გამოსახულებიდან p = p0 + ρgh გამომდინარეობს, რომ ნებისმიერი ფორმის, ერთგვაროვანი სითხით სავსე ზიარჭურჭელის ერთიდაიგივე დონის ნებისმიერ წერტილში წნევა ერთნაერია (ნახ. 4).
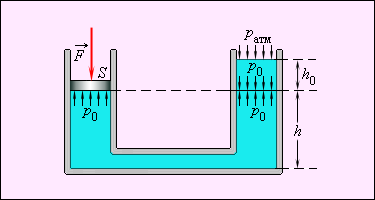
ნახ. 4. ზიარჭურჭლის მაგალითი. მარჯვენა მხარეს სითხის ზედაპირი ღიაა. ორივე მხარეს h დონეზე წნევა ერთნაერია და ტოლია p0 = F / S = ρgh0 + pატმ. ფსკერზე წნევა ტოლია p = p0 + ρgh
თუ ზიარჭურჭელის ორივე ვერტიკალურად განლაგებილ ცილინდრილ ნაწილს დგუშებით დავხურავთ, დგუშებზე მოდებული გარე ძალებით სითხეში შეიძლება ისეთი დიდი p წნევის შექმნა, რომელიც სისტემის ნებისმიერ წერთილში ბევრად მეტი იქნება ჰიდროდინამიკური ρgh წნევაზე. მაშინ შეიძლება ჩაითვალოს, რომ მთელ სისტემაში ერთნაერი p წნევა დამყარდა.თუ დგუშებს სხვადასხვა S1 და S2 ფართობები გააჩნიათ, მაშინ სითხის მხრიდან მათზე სხვადასხვა ძალა მოქმედებს F1 = pS1 და F2 = pS2. სისტემაში წონასწორობის შესანარჩუნებლად დგუშებზე მოდულით ასეთივე , მაგრამ საწინააღმდეგოდ მიმართული გარე ძალები უნდა იქნეს მოდებული. ამგვარად,
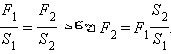
თუ S2 >> S1, მაშინ F2 >> F1. ასეთ ხელსაწყოებს ჰიდრავლიკურ წნეხს უწოდებენ (ნახ. 5). ისინი ძალაში მნიშვნელოვანი მოგების საშუალებას იძლევიან. თუ ვიწრო ცილინრის დგუშს 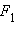 ძალის მოქმედებით
ძალის მოქმედებით  მანძილზე გადავაადგილებთ. მაშინ დგუში ფართო ცილინდრში მძიმე ტვირთს
მანძილზე გადავაადგილებთ. მაშინ დგუში ფართო ცილინდრში მძიმე ტვირთს 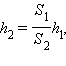 მანძილზე გადაადგილებს.
მანძილზე გადაადგილებს.
ამგვარად, ძალაში  მოგებას თან ახლავს ასეთივე წაგება მანძილში. ამასთან, ძალისა და მანძილის ნამრავლი უცვლევია:
მოგებას თან ახლავს ასეთივე წაგება მანძილში. ამასთან, ძალისა და მანძილის ნამრავლი უცვლევია:
F1h1 = F2h2.
ეს წესი სრულდება ნებისმიერი იდეალური მანქანისთვის, სადაც ხახუნის ძალები არ მოქმედებს. მას „მექანიკის ოქროს წესი“ეწოდება.

ნახ. 5. ჰიდრავლიკურიწნეხი. 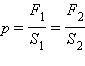
ჰიდრავლიკურ მანქანებს, რომლებსაც ტვირთის აწევისათვის იყენებენ, დომკრატებს უწოდებენ. მათ ფართოდ იყენებენ ჰიდრავლიკურ პრესადაც. სითხედ, ჩვეულებრივ, მინერალურ ზეთს იყენებენ.


{loadnavigation}
ფიზიკის ნაწილს, რომელიც სხეულის წონასწორობის პირობებს სწავლობს, სტატიკა ეწოდება. ნიუტონის მეორე კანონიდან გამომდინარეობს, რომ თუ სხეულზე მოდებული ყველა გაერე ძალის გეომეტრიული ჯამი ნულის ტოლია, სხეული უძრავია ან მოძრაობს წრფივად და თანაბრად. ამ დროს ამბობენ, რომ სხეუზე მოდებული ძალები აწონასწორებენ ერთმანეთს. გამოთვლებისას შეიძლება წარმოვიდგინოთ, რომ სხეულზე მოქმედი ყველა ძალის ტოლქმედი მასათა ცენტშია მოდებული.
არა მბრუნავი სხეულის წონასწორობისთვის, აუცილებელია, რომ სხეულზე მოდებული ყველა ძალის ტოლქმედი ნულის ტოლი იყოს.

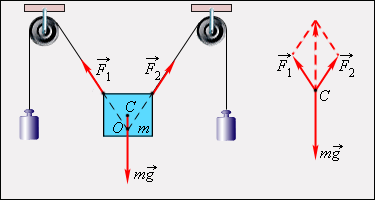
ნახ. 1. სამი ძალის მოქმედების ქვეშ მყოფი სხეულის წონასწორობა. გამოთვლებისას ყველა ძალის ტოლქმედი მიყვანილია ერთ C წერტილში
ნახ. 1–ზე სამი ძალის მოქმედების ქვეშ მყოფი სხეულის წონასწორობაა განხილული. 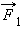 და
და ძალების გადაკვეთის წერტილი O არ ემთხვევა სიმძიმის ძალის მოდების წერტილს (C მასათა ცენტრი), მაგრამ წონასწორობისას ეს წერტილები აუცილებლად ერთ შვეულზე თავსდებიან. გამოთვლებისას ძალების ტოლქმედი ერთ წერტილზე მიიყვანება.
ძალების გადაკვეთის წერტილი O არ ემთხვევა სიმძიმის ძალის მოდების წერტილს (C მასათა ცენტრი), მაგრამ წონასწორობისას ეს წერტილები აუცილებლად ერთ შვეულზე თავსდებიან. გამოთვლებისას ძალების ტოლქმედი ერთ წერტილზე მიიყვანება.
თუ სხეულს გარკვეული ღერძის გარშემო ბრუნვა შეუძლია, მისი წომასწორობისათვის საკმარისი არ არის, რომ ყველა ძალის ტოლქმედი ნულის ტოლი იყოს.
ძალის მაბრუნებელი მოქმედება დამოკიდებულია არა მხოლოდ მის სიდიდეზე, არამედ ბრუნვის ღერძსა და ძალის მოქმედების წრფეს შორის მანძილზე.
ბრუნვის ღერძსა და ძალის მოქმედების წრფეს შორის გავლებული შვეულის სიგრზეს ძალის მხარს უწოდებენ.
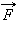 ძალის მოდულისა და d მხარის ნამრავლს M–ს ძალის მომენტი ეწოდება. დადებითად თვლიან იმ ძალის მომენტებს, რომლებიც სხეულს საათის ისრის ბრუნვის საწინააღმდეგოდ აბრუნებს. (ნახ. 2).
ძალის მოდულისა და d მხარის ნამრავლს M–ს ძალის მომენტი ეწოდება. დადებითად თვლიან იმ ძალის მომენტებს, რომლებიც სხეულს საათის ისრის ბრუნვის საწინააღმდეგოდ აბრუნებს. (ნახ. 2).
მომენტების წესი: უძრავი ბრუნვის ღერძის მქონე სხეული წონასწორობაში იმყოფება, თუ სხეულზე მოდებული ყველა ძალის მომენტების ალგებრული ჯამი ამ ღერძის მიმართ ნულის ტოლია:
M1 + M2 + ... = 0.
ერთეულთა სართაშორისო სისტემაში ძალის მომენტი იზომება ნიუტონ–მეტრში (ნ.მ).
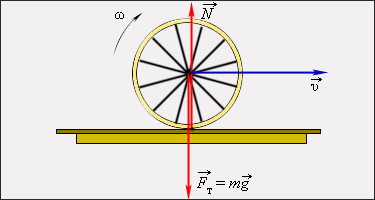
ნახ. 2. ბერკეტზე მოქმედი ძალები და მათი მომენტები. M1 = F1 · d1 > 0; M2 = – F2 · d2 < 0. წონასწორობისას M1 + M2 = 0
ზოგად შემთხვევაში, როცა სხეულს ბრუნვითი და გადატანითი მოძრაობა შეუძლია, წონასწორობისათვის ორივე პორობა აუცილებლად უნდა სრულდებოდეს: ტოლქმედი ძალაც და მომენტების ჯამიც ნულის ტოლი უნდა იყოს.
ორივე ეს პირობა არ არის საკმარისი უძრაობის მდგომარეობისათვის.
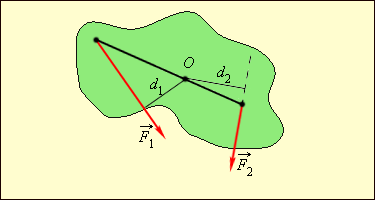
ნახ. 3. ბორბლის გორვა ჰორიზონტალორ ზედაპირზე. ტოლქმედი ძალა და მომენტების ჯამი ნულის ტოლი
ჰორიზონტალორ ზედაპირზე მგორავი ბორბალი განურჩეველი წონასწორობის მაგალითს წარმოადგენს (ნახ. 3). ბორბალი რომ ნებისმიერ წერტილში გავაჩეროთ, ის წონასწორულ მდგომარეობაში აღმოჩნდება. განურჩველი წონასწორობის გარდა მექანიკაში არჩევენ მდგრადი და არამდგრადი წონასწორობების მდგომარეობებს.
წონასწორობის მდგომარეობას უწოდებენ მდგრადს, თუ ამ მდგომარეობიდან სხეულის მცირე გადახრისას აღიძვრება ძალები ან ძალის მომენტები, როლებიც ცდილობენ სხეულის წონასწორობის მდგომარეობაში დაბრუნებას.
არამდგრადი წონასწორობის მდგომარეობიდან სხეულის მცირე გადახრისას აღიძვრება ძალები ან ძალის მომენტები, როლებიც ცდილობენ სხეულის წონასწორობის მდგომარეობიდან დაშორებას.
ბრტყელ ჰორიზონტულ სიბრტყეზე მდებარე ბურთი განურჩეველი წონასწორობის მდგომარეობაში იმყოფება. სფერული ზედაპირის ზედა წერტილში მდებარე ბურთი – არამდგრადი წონასწორობის მაგალითია. და ბოლოს სფერული ჩაღრმავების ფსკერზე მდებარე ბურთი მდგრად წომასწორობაშია (ნახ. 4).

ნახ. 4, საყრდენზე მყოფი ბურთის წონასწორობის სხვადასხვა სახეები. 1– განურჩეველი წონასწორობა, (2) – მდგრად წომასწორობა, (3) – არამდგრადი წონასწორობა
მოძრავი ბრუნვის ღერძის მქონე სხეულისათვის წონასწორობის სამივე სახეა შესაძლებელი.განურჩეველი წონასწორობა წარმოიშვება, როცა ბუნვის ღერძი მასათა ცენტრზე გადის. მდგრადი და არამდგრადი წონასწორობებისას მასათა ცენტრი მდებარეობს ბრუნვის ღერძზე გამავალ ვერტიკალურ წრფეზე, ამასთან, თუ მასათა ცენტრი ბრუნვის ღერძის დაბლა მდებარეობს წონასწორობის მდგომარეობა მდგრადია (ნახ. 5).
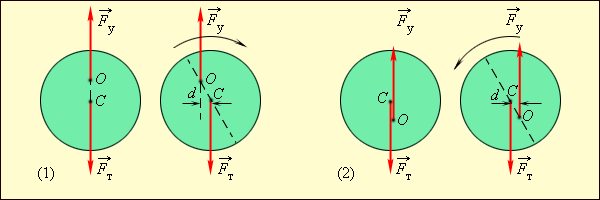
ნახ. 5. O ღერძზე გამაგრაბული ერთგვაროვანი წრიული დისკოს მდგრადი (1) და არამდგრადი (2) წონასწორობა. C წერტილი – დისკო მასათა ცენტრი; 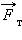 – სიმძიმის ძალა;
– სიმძიმის ძალა; 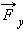 – ღერძის დაჭიმულობის ძალა; d – მხარი
– ღერძის დაჭიმულობის ძალა; d – მხარი
განსაკუთრების შემთხვევას წარმოადგენს სხეული საყრდენზე. ამ დროს საყრდენის დრეკადობის ძალა მოდებულია არ მხოლოდ ერთ წერტილში, არამედ განაწილებულია მთელ საყრდენზე (ფუძეზე). სხეული წონასწორობაშია თუ მასათა ცენტრზე გავლებული შვეული საყრდენ ფართობზე გადის. თუ ეს ხაზი საყრდენის ფართობს არ კვეთს, სხეული წაიქცევა. ასეთი სსხეულის კარგ მაგალითს წარმოადგენს გადახრილი კოშკი იტალიის ქალაქ პიზაში (ნახ. 6), რომელსაც როგორც გადმოცემა გვაუწყებს გალილეი თავისუფალი ვარდნის კანონების შესწავლისას იყენებდა. კოშკს ცილინდრის ფორმა აქვს, რომლის სიმაღლე 55 მ და რადიუსი 7 მ–ა. კოშკის მწვერვალი შვეულიდან 4,5 მ–ზეა გადახრილი.
კოშკის მასათა ცენტრზე გამავალი შვეული საყრდენს ცენტრიდან 2,3 მ–ზე კვეთს. ამგვარად კოშკი წონასწორობაშია.წონასწორობა დაირღვევა და კოშკი წაიქცევა, როცა მისი მწვერვალის შვეულიდან გადახრა 14 მ–ს მიაღწევს.როგოც ჩანს ეს არც ისე მალე მოხდება.

ნახ. 6. პიზის გადახრილი კოშკი. C– მასათა ცენტრი, O – კოშკის საყრდენის ცენტრი, CC' – მასათა ცენტრზე გამავალი შვეული
