სითხის ძირითადი განსხვავება მყარი (დრეკადი) სხეულიბისაგან, მის მიერ ფორმის ადვილად შეცვლის უნარია (სითხე ვერ ინარჩულებს ფორმას). სითხის ნაწილებს შეუძლიათ თავისუფლად იმოძრაონ, ისრიალონ ერთმანეთის მიმართ. ამიტომაც სითხე ღებულობს იმ ჭურჭლის ფორმას, რომელშიაც ისაა ჩასხმული. სითხეში, ისევე როგორც აირის გარემოში, შეიძლება ჩავძიროთ მყარი სხეული. აირისაგან განსხვავებით სითხეები პრაქტიკულად არ იკუმშებიან.
სითხეში ჩაძირულ სხეულზე მოქმედებენ ძალები, რომლების სხეულის ზედაპირზე არიან განაწილებული. ასე განაწილებილი ძალების აღწერისათვის შემოყვანილია ახალი ფიზიკური სიდიდე – წნევა.
წნევა განისაზღვრება როგოც, ზედაპირის მართობულად მომქმედი ძალის 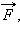 მოდულის ფარდობა ამ ზედაპირის ფართობთან S :
მოდულის ფარდობა ამ ზედაპირის ფართობთან S :
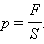
SI სისტემაში წნევა იზომება პასკალებში (პა):
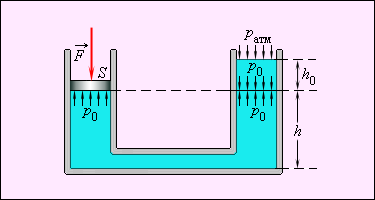
1 პა = 1 ნ/მ2.
ხშირად გამოიყენება სისტემის გარეშე ერთეულები: ნორმალური ატმოსფერული წნევა (ატმ) და ვერცხლისწყლის სვეტის მილიმეტრი (მმHg):
1 ატმ=101325 პა=760 მმHg
ფრანგმა მეცნიერმა ბ.პასკალმა, XVII საუკუნეში, ემპირიულად დაადგინა კანონი, რომელსაც პასკალის კანონი ეწოდება:
სითხესა და აირში წნევა ყველა მიმართულების ერთნაირად გადაეცემა დ არ არის დამოკიდებული იმ ზედაპირის ორიენტაციაზე, რომელზეც ის მოქმედებს.
პასკალის კანონის საილუსტრაციოდ ნახ. 1–ზე სითხეში ჩაძირული პატარა მართკუთხა პრიზმაა გამოსახული. თუ დავუშვებთ, რომ პრიზმის მასალის სიმკვრივე სითხის სიმკვრივის ტოლია, მაშინ პრიზმა სითხეში განურჩეველი წონასწორობის მდგომარეობაში უნდა იმყოფებოდეს. ეს იმას ნიშნავს, რომ პრიზმის წახნაგებზე მომქმედი წნევის ძალები გაწონასწორებული უნდა იყვნენ. ეს მხოლოდ იმ შემთხვევაში მოხდება, თუ წნევა, ე.ი. ძალები, პრიზმის ყოველი წახნაგის ფართობის ერთეულზე, ერთნაირია: p1 = p2 = p3 = p.

ნახ. 1. პასკალის კანონი:p1 = p2 = p3 = p
წნევა სითხეში ჭურჭლის ფსკერზე და კედლებზე სითხის სვეტის სიმაღლეზეა დამოკიდებული.
სითხის წნევა, h სიმაღლისა და ფსკერის S ფართობის მქონე ცილინდრული ჭურჭლის ფსკერზე, სითხის mg სვეტის წონის ტოლია, სადაც m = ρghS – ჭურჭელში არსებული სითხის მასაა, ρ – სითხის სიმკვრივე. შესაბამისად
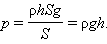
პასკალის კანონის მიხედვით სითხე h სიმაღლეზე ჭურჭლის გვერდით კიდლებზე ასეთივე წნევას ქმნის. სითხის ρgh სვეტის წნევას ჰიდროსტატიკურ წნევას უწოდებენ.
თუ სითხე იმყოფება დგუშიან ცილინდრში (ნახ. 2), მაშინ დგუშზე რაღაც გარე 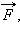 ძალით მოქმედებისას, სითხეში შეიძლება დამატებითი წნევა შეიქმნას p0 = F / S, სადაც S – დგუშის ფართობია.
ძალით მოქმედებისას, სითხეში შეიძლება დამატებითი წნევა შეიქმნას p0 = F / S, სადაც S – დგუშის ფართობია.
ამგვარად, სრული წნევა სითხეში h სიღრმეზე შეიძლება შემდეგი სახით ჩაიწეროს:
p = p0 + ρgh.
თუ ნახ. 2–ს დგუშს მოვაცილებთ, მაშინ სითხის ზედაპირზე წნევა ატმოსფერული წნევის ტოლი იქნება: p0 = pატმ.

ნახ. 2. წნევის დამოკიდებულიბა სითხის სვეტის სიმაღლეზე
სითხის სხვადასხვა დონეზე წნევების განსხვავების გამო აღიძვრება ამომგდები ანუ არქიმედეს ძალა 
ნახ. 2 ხსნის არქიმედეს ძალის მოქმედებას. სითხეში, h და S ფუძის ფართობის მქონე, მართკუთხა პარალელეპიპედის ფორმის სხეულია ჩაშვებული. ზედა და ქვედა წახნაგებზე წნევათა სხვაობა ტოლია:
Δp = p2 – p1 = ρgh
ამიტომაც ამომგდები ძალა 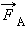 ზევითაა მიმართული და სიდიდით ტოლია
ზევითაა მიმართული და სიდიდით ტოლია
FА = F2 – F1 = SΔp = ρgSh = ρgV
სადაც V – სხეულის მიერ გამოდევნილი სითხის მიცულობაა, ხოლო ρV – მისი მასა.
სითხეში (ან აირში) ჩაშვებულ სხეულზე მომქმედი არქიმედეს ძალა სხეულის მიერ გამოდევნილი სითხის (ან აირის) წონის ტოლია. არქიმედეს კანონად წოდებული ეს მტკიცება ნებისმიერი ფორმის სხეულისათვისაა სამართლიანი.
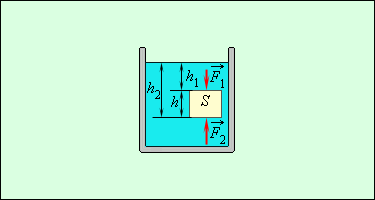
ნახ. 3.
არქიმედეს კანონი. FА = F2 – F1 = S(p2 – p1) = ρgSh, F1 = p1S,F2 = p2S
არქიმედას კანონიდან გამომდინარეობს, რომ თუ სხეულის საშუალო სიმკვრივე ρსხ სითხის (აირის) ρ სიმკვრივეზე მეტია, მაშინ სხეული ფსკერზე ჩაიძირება. თუ ρსხ< ρ, სხეული სითხის ზედაპირზე იცურებს. სხეულის სითხეში ჩაძირული ნაწილის მოცულობა იქნება ისეთი, რომ გამოდევნილი სითხის წონა ტოლი იქნება სხეულის წონისა. საჰაერო ბუშტის ჰაერში ასაფრენად მისი წონა ნაკლები უნდა იყოს გამოდევნილი ჰაერს წონისა. ამიტომაც, საჰაერო ბუშტებს მსუბუქი აირებით (წყალბადითა, ჰელიუმით) ან გამთბარი ჰაერით ბერავენ.
სითხეში სრული წნევის გამოსახულებიდან p = p0 + ρgh გამომდინარეობს, რომ ნებისმიერი ფორმის, ერთგვაროვანი სითხით სავსე ზიარჭურჭელის ერთიდაიგივე დონის ნებისმიერ წერტილში წნევა ერთნაერია (ნახ. 4).
ნახ. 4. ზიარჭურჭლის მაგალითი. მარჯვენა მხარეს სითხის ზედაპირი ღიაა. ორივე მხარეს h დონეზე წნევა ერთნაერია და ტოლია p0 = F / S = ρgh0 + pატმ. ფსკერზე წნევა ტოლია p = p0 + ρgh
თუ ზიარჭურჭელის ორივე ვერტიკალურად განლაგებილ ცილინდრილ ნაწილს დგუშებით დავხურავთ, დგუშებზე მოდებული გარე ძალებით სითხეში შეიძლება ისეთი დიდი p წნევის შექმნა, რომელიც სისტემის ნებისმიერ წერთილში ბევრად მეტი იქნება ჰიდროდინამიკური ρgh წნევაზე. მაშინ შეიძლება ჩაითვალოს, რომ მთელ სისტემაში ერთნაერი p წნევა დამყარდა.თუ დგუშებს სხვადასხვა S1 და S2 ფართობები გააჩნიათ, მაშინ სითხის მხრიდან მათზე სხვადასხვა ძალა მოქმედებს F1 = pS1 და F2 = pS2. სისტემაში წონასწორობის შესანარჩუნებლად დგუშებზე მოდულით ასეთივე , მაგრამ საწინააღმდეგოდ მიმართული გარე ძალები უნდა იქნეს მოდებული. ამგვარად,
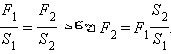
თუ S2 >> S1, მაშინ F2 >> F1. ასეთ ხელსაწყოებს ჰიდრავლიკურ წნეხს უწოდებენ (ნახ. 5). ისინი ძალაში მნიშვნელოვანი მოგების საშუალებას იძლევიან. თუ ვიწრო ცილინრის დგუშს 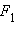 ძალის მოქმედებით
ძალის მოქმედებით  მანძილზე გადავაადგილებთ. მაშინ დგუში ფართო ცილინდრში მძიმე ტვირთს
მანძილზე გადავაადგილებთ. მაშინ დგუში ფართო ცილინდრში მძიმე ტვირთს 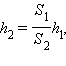 მანძილზე გადაადგილებს.
მანძილზე გადაადგილებს.
ამგვარად, ძალაში  მოგებას თან ახლავს ასეთივე წაგება მანძილში. ამასთან, ძალისა და მანძილის ნამრავლი უცვლევია:
მოგებას თან ახლავს ასეთივე წაგება მანძილში. ამასთან, ძალისა და მანძილის ნამრავლი უცვლევია:
F1h1 = F2h2.
ეს წესი სრულდება ნებისმიერი იდეალური მანქანისთვის, სადაც ხახუნის ძალები არ მოქმედებს. მას „მექანიკის ოქროს წესი“ეწოდება.

ნახ. 5. ჰიდრავლიკურიწნეხი. 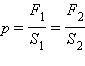
ჰიდრავლიკურ მანქანებს, რომლებსაც ტვირთის აწევისათვის იყენებენ, დომკრატებს უწოდებენ. მათ ფართოდ იყენებენ ჰიდრავლიკურ პრესადაც. სითხედ, ჩვეულებრივ, მინერალურ ზეთს იყენებენ.




