ფიზიკის ნაწილს, რომელიც სხეულის წონასწორობის პირობებს სწავლობს, სტატიკა ეწოდება. ნიუტონის მეორე კანონიდან გამომდინარეობს, რომ თუ სხეულზე მოდებული ყველა გაერე ძალის გეომეტრიული ჯამი ნულის ტოლია, სხეული უძრავია ან მოძრაობს წრფივად და თანაბრად. ამ დროს ამბობენ, რომ სხეუზე მოდებული ძალები აწონასწორებენ ერთმანეთს. გამოთვლებისას შეიძლება წარმოვიდგინოთ, რომ სხეულზე მოქმედი ყველა ძალის ტოლქმედი მასათა ცენტშია მოდებული.
არა მბრუნავი სხეულის წონასწორობისთვის, აუცილებელია, რომ სხეულზე მოდებული ყველა ძალის ტოლქმედი ნულის ტოლი იყოს.
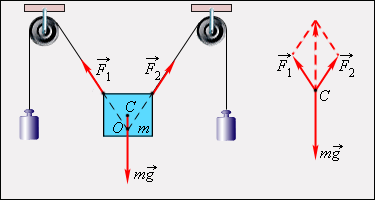
ნახ. 1. სამი ძალის მოქმედების ქვეშ მყოფი სხეულის წონასწორობა. გამოთვლებისას ყველა ძალის ტოლქმედი მიყვანილია ერთ C წერტილში
ნახ. 1–ზე სამი ძალის მოქმედების ქვეშ მყოფი სხეულის წონასწორობაა განხილული. 
და
ძალების გადაკვეთის წერტილი O არ ემთხვევა სიმძიმის ძალის მოდების წერტილს (C მასათა ცენტრი), მაგრამ წონასწორობისას ეს წერტილები აუცილებლად ერთ შვეულზე თავსდებიან. გამოთვლებისას ძალების ტოლქმედი ერთ წერტილზე მიიყვანება.
თუ სხეულს გარკვეული ღერძის გარშემო ბრუნვა შეუძლია, მისი წომასწორობისათვის საკმარისი არ არის, რომ ყველა ძალის ტოლქმედი ნულის ტოლი იყოს.
ძალის მაბრუნებელი მოქმედება დამოკიდებულია არა მხოლოდ მის სიდიდეზე, არამედ ბრუნვის ღერძსა და ძალის მოქმედების წრფეს შორის მანძილზე.
ბრუნვის ღერძსა და ძალის მოქმედების წრფეს შორის გავლებული შვეულის სიგრზეს ძალის მხარს უწოდებენ.
ძალის მოდულისა და d მხარის ნამრავლს M–ს ძალის მომენტი ეწოდება. დადებითად თვლიან იმ ძალის მომენტებს, რომლებიც სხეულს საათის ისრის ბრუნვის საწინააღმდეგოდ აბრუნებს. (ნახ. 2).
მომენტების წესი: უძრავი ბრუნვის ღერძის მქონე სხეული წონასწორობაში იმყოფება, თუ სხეულზე მოდებული ყველა ძალის მომენტების ალგებრული ჯამი ამ ღერძის მიმართ ნულის ტოლია:
M1 + M2 + ... = 0.
ერთეულთა სართაშორისო სისტემაში ძალის მომენტი იზომება ნიუტონ–მეტრში (ნ.მ).
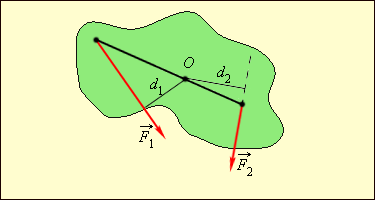
ნახ. 2. ბერკეტზე მოქმედი ძალები და მათი მომენტები. M1 = F1 · d1 > 0; M2 = – F2 · d2 < 0. წონასწორობისას M1 + M2 = 0
ზოგად შემთხვევაში, როცა სხეულს ბრუნვითი და გადატანითი მოძრაობა შეუძლია, წონასწორობისათვის ორივე პორობა აუცილებლად უნდა სრულდებოდეს: ტოლქმედი ძალაც და მომენტების ჯამიც ნულის ტოლი უნდა იყოს.
ორივე ეს პირობა არ არის საკმარისი უძრაობის მდგომარეობისათვის.
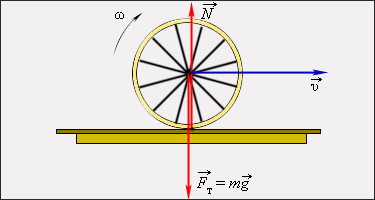
ნახ. 3. ბორბლის გორვა ჰორიზონტალორ ზედაპირზე. ტოლქმედი ძალა და მომენტების ჯამი ნულის ტოლი
ჰორიზონტალორ ზედაპირზე მგორავი ბორბალი განურჩეველი წონასწორობის მაგალითს წარმოადგენს (ნახ. 3). ბორბალი რომ ნებისმიერ წერტილში გავაჩეროთ, ის წონასწორულ მდგომარეობაში აღმოჩნდება. განურჩველი წონასწორობის გარდა მექანიკაში არჩევენ მდგრადი და არამდგრადი წონასწორობების მდგომარეობებს.
წონასწორობის მდგომარეობას უწოდებენ მდგრადს, თუ ამ მდგომარეობიდან სხეულის მცირე გადახრისას აღიძვრება ძალები ან ძალის მომენტები, როლებიც ცდილობენ სხეულის წონასწორობის მდგომარეობაში დაბრუნებას.
არამდგრადი წონასწორობის მდგომარეობიდან სხეულის მცირე გადახრისას აღიძვრება ძალები ან ძალის მომენტები, როლებიც ცდილობენ სხეულის წონასწორობის მდგომარეობიდან დაშორებას.
ბრტყელ ჰორიზონტულ სიბრტყეზე მდებარე ბურთი განურჩეველი წონასწორობის მდგომარეობაში იმყოფება. სფერული ზედაპირის ზედა წერტილში მდებარე ბურთი – არამდგრადი წონასწორობის მაგალითია. და ბოლოს სფერული ჩაღრმავების ფსკერზე მდებარე ბურთი მდგრად წომასწორობაშია (ნახ. 4).
ნახ. 4, საყრდენზე მყოფი ბურთის წონასწორობის სხვადასხვა სახეები. 1– განურჩეველი წონასწორობა, (2) – მდგრად წომასწორობა, (3) – არამდგრადი წონასწორობა
მოძრავი ბრუნვის ღერძის მქონე სხეულისათვის წონასწორობის სამივე სახეა შესაძლებელი.განურჩეველი წონასწორობა წარმოიშვება, როცა ბუნვის ღერძი მასათა ცენტრზე გადის. მდგრადი და არამდგრადი წონასწორობებისას მასათა ცენტრი მდებარეობს ბრუნვის ღერძზე გამავალ ვერტიკალურ წრფეზე, ამასთან, თუ მასათა ცენტრი ბრუნვის ღერძის დაბლა მდებარეობს წონასწორობის მდგომარეობა მდგრადია (ნახ. 5).
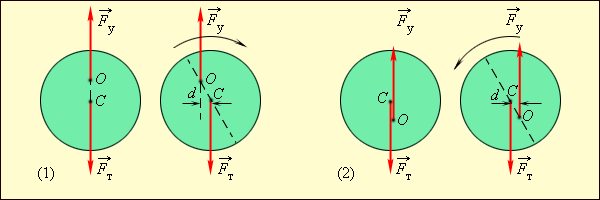
ნახ. 5. O ღერძზე გამაგრაბული ერთგვაროვანი წრიული დისკოს მდგრადი (1) და არამდგრადი (2) წონასწორობა. C წერტილი – დისკო მასათა ცენტრი;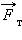 
– სიმძიმის ძალა; 
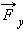– ღერძის დაჭიმულობის ძალა; d – მხარი
განსაკუთრების შემთხვევას წარმოადგენს სხეული საყრდენზე. ამ დროს საყრდენის დრეკადობის ძალა მოდებულია არ მხოლოდ ერთ წერტილში, არამედ განაწილებულია მთელ საყრდენზე (ფუძეზე). სხეული წონასწორობაშია თუ მასათა ცენტრზე გავლებული შვეული საყრდენ ფართობზე გადის. თუ ეს ხაზი საყრდენის ფართობს არ კვეთს, სხეული წაიქცევა. ასეთი სსხეულის კარგ მაგალითს წარმოადგენს გადახრილი კოშკი იტალიის ქალაქ პიზაში (ნახ. 6), რომელსაც როგორც გადმოცემა გვაუწყებს გალილეი თავისუფალი ვარდნის კანონების შესწავლისას იყენებდა. კოშკს ცილინდრის ფორმა აქვს, რომლის სიმაღლე 55 მ და რადიუსი 7 მ–ა. კოშკის მწვერვალი შვეულიდან 4,5 მ–ზეა გადახრილი.
კოშკის მასათა ცენტრზე გამავალი შვეული საყრდენს ცენტრიდან 2,3 მ–ზე კვეთს. ამგვარად კოშკი წონასწორობაშია.წონასწორობა დაირღვევა და კოშკი წაიქცევა, როცა მისი მწვერვალის შვეულიდან გადახრა 14 მ–ს მიაღწევს.როგოც ჩანს ეს არც ისე მალე მოხდება.
ნახ. 6. პიზის გადახრილი კოშკი. C– მასათა ცენტრი, O – კოშკის საყრდენის ცენტრი, CC' – მასათა ცენტრზე გამავალი შვეული