{loadnavigation}

ატომისა და ელემენტარული ნაწილაკების სამყაროში გრავიტაციული ძალების უგულვებელყოფა შესაძლებელია, მათი, ნაწილაკებს შორის სხვა სახის ურთიერთქმედების ძალებთან შედარებითი, საგრძნობი სიმცირის გამო. ასევე, ჩვენ გარმომცველ  სხეულებს შორისაც ძალიან რთულია გრავიტაციული ურთიერთქმედების დაკვირვება, მაშინაც კი თუ მათი მასები რამოდენიმე ათას კილოგრამს შეადგენს. მაგრამ სწორედ გრავიტაცია განსაზღვრავს ისეთი „დიდი“ ობიექტების, როგორიცაა პლანეტები, კომეტები ვარსკვლავები, ყოფაქცევას და სწორედ გრავიტაცია  აკავებს ყველას და ყველაფერს დედამიწაზე.

გრავიტაცია მართავს პლანეტების მოძრაობას მზის სისტემაში. გრავიტაციის გარაშე, მზის სისტემის შემადგენელი პლანეტები სხვადასხვა მხარეს გაიქცეოდნენ და სამყაროს უკიდეგანო სივრცეში დაიკარგებოდნენ.

 

პლანეტების მოძრაობის კანონზომიერებები უხსოვარი დროიდან იპყრობდა ადამიანის ყურადღებას. პლანეტების მოძრაობისა  და მზის სისტემის აგებულების შესწავლა გახდა გრავიტაციის თეორიის შექმნის – მსოფლიო მიზიდულობის კანონების აღმოჩენის მიზეზი.

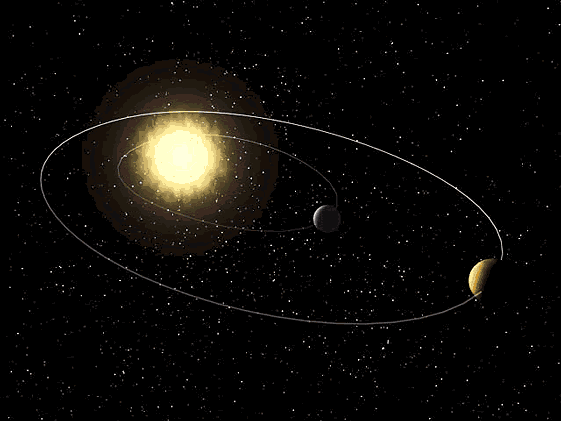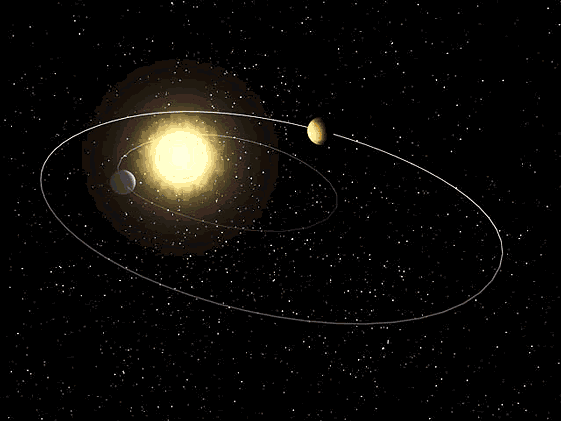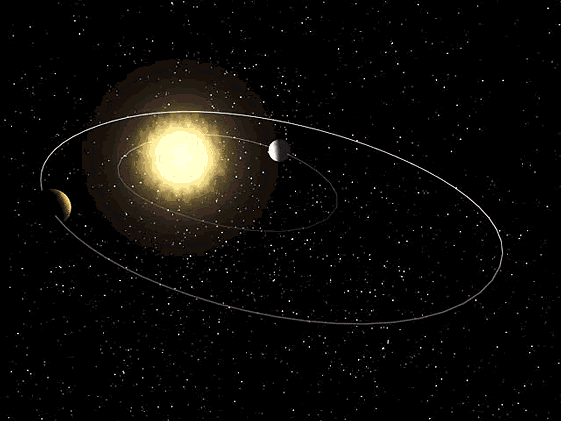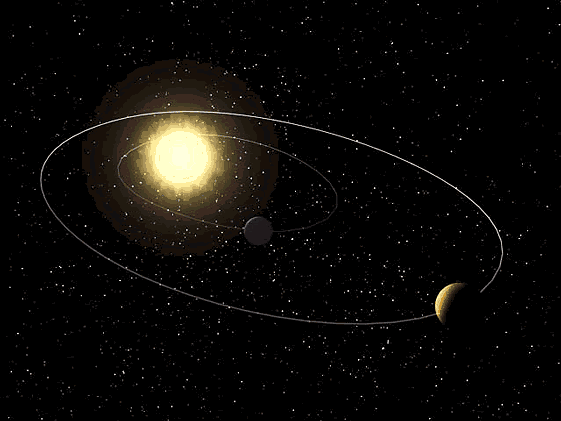
დედამიწაზე მყოფი დამკვირვებლის თვალსაზრისით, პლანეტები საკმაოდ რთულ ტრაექტორიებზე მოძრაობენ (ნახ. 1). სამყაროს მოდელის შექმნის პირველი მცდელობა პტოლემეს ეკუთვნის (~140წ.). პტოლემემ სამყაროს ცენტრში დედამიწა მოათავსა, რომლის გარშემოც დიდ და მცირე წრეებზე პლანეტები და ვარსკვალევები მოძრაობენ.

ნახ. 1.

ვარსკვალვების ფონზე მარსის მოძრაობის პირობითი ტრაექტორია

პტოლემეს გეოცენტრულმა სისტემამ  14 ასწლელული გაძლო და მხოლოდ  XVI  საუკუნის შუაში იგი კოპერნიკის ჰელიოცენტრულმა სისტემამ ჩაანაცვლა. კოპერნიკის სისტემაში პლანეტების ტრაექტორიები უფრო მარტივი აღმოჩნდა.

გერმანელმა ასტრონომმა კეპლერმა XVII საუკუნის დასაწყისში კოპერნიკის სისტემის საფუძველზე მზის სისტემის პლანეტების მოძრაობის სამი ემპირიული კანონი ჩამოაყალიბა. კეპლერი დანიელი ასტრონომის ტიხო ბრაგეს პლანეტების მოძრაობაზე დაკვივებებს იყენებდა.

კეპლერის პირველი კანონი (1609 წ.):

ყოველი პლენეტის  ორბიტა  ელიფსია,  რომლის ერთ–ერთ ფოკუსში მოთავსებულია მზე.

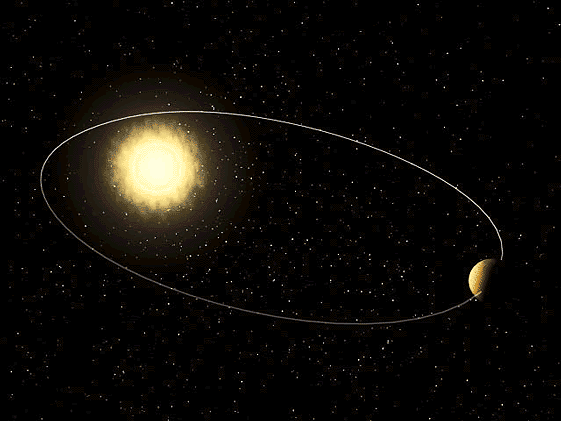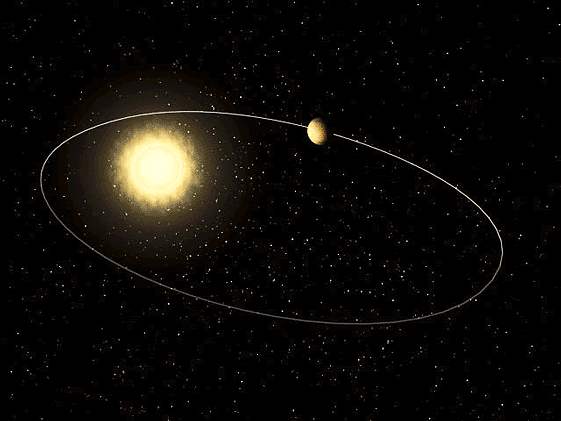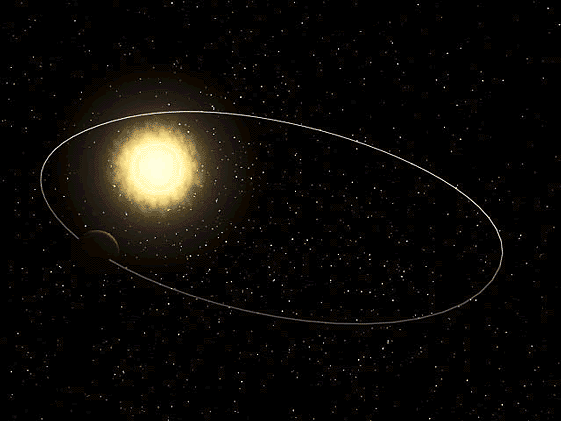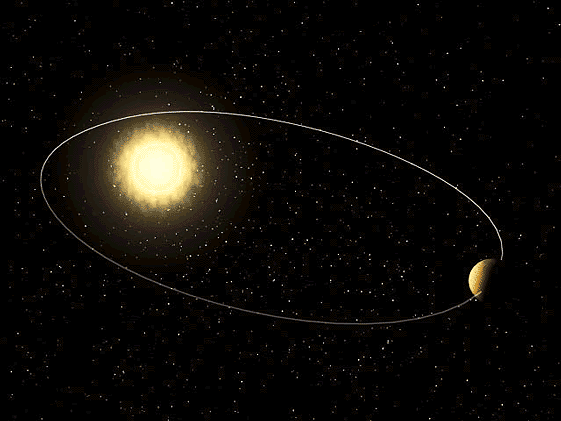
ნახ. 2–ზე მზის მასაზე გაცილების ნალკები მასის მქონე პლანეტის ელიფსური ორბიტაა ნაჩვენები. მზე ელიფსის ერთ–ერთ ფოკუსში მდებარეობს. ტრაექტორიის მზესთან უახლოესი წერტილ  \(P\) –ს პერიჰელიუმი ეწოდება, მზიდან მაქსიმალურად დაშორებულ წერტილს \(A\) –ს – აფელიუმი. აფელიუმსა და პერიჰელიუმს შორის მანძილი ელიფსის დიდი ღერძია.

ნახ. 2.

\(m<<M\)  მასის პლანეტის ელიფსური ორბიტა. \(a\) – დიდი ნახევარღერძის სიგრძე, \(F\) და \(F^{'}\)  – ელიფსის ფოკუსები.

მზის სისტემის თითქმის ყველა პლანეტა (გარდა პლუტონისა) მოძრაობს წრეწირის მახლობელ ორბიტაზე.

კეპლერის მეორე კანონი (1609 წ.):

ყოველი პლანეტის რადიუს–ვექტორი დროის თანატოლ შუალედებში თანატოლ ფართობებს შემოწერს.

ნახ. 3  კეპლერის მეორე კანონის გრაფიკული ილუსტრაციას წარმოადგენს.

 

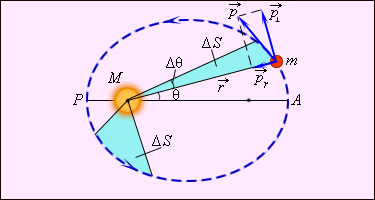
ნახ. 3.

კეპლერის მეორე კანონი – ფართობების კანონი.

კეპლერის მეორე კანონი იმპულსის მომენტების მუდმივობის კანონის ექვივალენტურია. ნახ. 3–ზე გამოსახულია სხეულის  \(\vec{p}\)  იმპულსი და მისი მდგენელები \(\vec{p}_{r}\) და \(\vec{p}_{\perp }\)   მცირე \(\Delta t\)  დროში რადიუს–ვექტორის მიერ შემოწერილი ფართობი ტოლია \(r\Delta \Theta\)  ფუძისა და  \(r\)   სიმაღლის მქონე სამკუთხედის ფართობისა: 

\(\Delta S=\frac{1}{2}r^{2}\Delta \Theta\)   ან  \(\frac{\Delta S}{\Delta t}=\frac{1}{2}r^{2}\frac{\Delta\Theta }{\Delta t}=\frac{1}{2}r^{2}\omega ;\: (\Delta t\rightarrow 0).\)

აქ  \(\omega =\frac{\Delta \Theta }{\Delta t};\: (\Delta t\rightarrow 0)\) –კუთხური სიჩქარეა.

იმპულსის მომენტი \(L\)  აბსოლუტური სიდიდით ტოლია  \(\vec{p}_{\perp }\) და \(\vec{r}\) ვექტორების მოდულების ნამრავლისა:

  \(L=rp_{\perp }=r(mv_{\perp })=mr^{2}\omega\) , რადგან \(v_{\perp}=r\omega.\)

ამ თანაფარდობებიდან გამოდის:

\(\frac{\Delta S}{\Delta t}=\frac{L}{2m};\: (\Delta t\rightarrow 0).\)

ამიტომ, თუ კეპლერის კანონის მიხედვით \(\frac{\Delta S}{\Delta t} =const\) , მაშინ იმპულსის მომენტი \(L\)  მოძრაობისას  უცვლელი რჩება.

კერძოდ, რადგან პლანეტის სიჩქარეები პერიჰელიუმში \(\vec{v}_{P}\)  და აფელიუმში \(\vec{v}_{A}\) ვექტორები მიმართულია \(\vec{r}_{P}\)  და  \(\vec{r}_{A}\)  რადიუს–ვექტორების მართობულად, იმპულსის მომენტების მუდმივობის კანონიდან გამომდინარე:

\(r_{P}v_{P}=r_{A}v_{A}.\)

კეპლერის მესამე კანონი (1619 წ.):

პლანეტების გარშემოქცევის პერიოდთა კვადრატების შეფარდება ორბიტის დიდი ნახევარღერძების კუბებთან მუდმივი სიდიდეა.

 \(\frac{T^{2}}{a^{3}}=const\)   ან  \(\frac{T_{1}^{2}}{a_{1}^{3}}=\frac{T_{2}^{2}}{a_{2}^{3}}.\)

კეპლერის მესამე კანონი მზის სისტემის ყველა პლანეტისათვის ხორციელდება  1 %–ანი სიზუსტით.

ნახ. 4–ზე გამოსახულია ორი ორბიტა, ერთ–ერთი – წრიული  \(R\) რადიუსით, მეორე კი – \(a\) –ს ტოლი დიდი ნახევარღერძის მქონე ელიფსი. მესამე კანონი ამტკიცებს, რომ თუ \(R=a\) , მაშინ სხეულების გარშემოვლის პერიოდები ერთნაირია.

ნახ. 4.

წრიული და ელიფსური ორბიტები. როცა  \(R=a\) , მაშინ სხეულების გარშემოვლეს პერიოდები ერთნაირია.

იმისდა მიუხედავად რომ, კეპლერის კანონები პლანეტების მოძრაობის შეცნობაში უმნიშვნელოვანეს ეტაპს წარმოადგენდა, ისინი მაინც მხოლოდ ასტრონომიული დაკვირვებებიდან მიღებულ ემპირიულ კანონებად რჩებოდა. გადამწყვეტი ნაბიჯი ამ მიმართულებით ისააკ ნიუტონმა 1682 წელს მსოფლიო მიზიდულობის კანონის აღმოჩენით გადადგა.

\(F=G\frac{Mm}{r^{2}},\)

სადაც \(M\)  და \(m\) – მზისა და პლანეტის მასებია, r – მათ შორის მანძილი,  G = 6,67·10^–11 ნ·მ²/კგ² –  გრავიტაციული მუდმივა. ნიუტონმა პირველმა გამოთქვა მოსაზრება, რომ გრავიტაციული ძალები განსაზღვრავენ არა მხოლოდ ზმის სისტემების პლანეტების მოძრაობას; ისინი სამყაროს ნებისმიერ სხეულებს შორის მოქმედებენ. კერძოდ, ის მაშინვე ამბობდა რომ, დედამიწის ზედაპირის მახლობლად მოქმედ სიმძიმის ძალას გარავიტაციული ბუნება აქვს.

წრიული ორბიტებისათვის კეპლერის პირველი და მეორე კანონები ავტომატურად სრულდება, ხოლო მესამე კანონის მიხედვით \(T^{2}\sim R^{3}\), სადაც \(T\) – ბრუნვის პერიოდია, \(R\) – ორბიტის რადიუსი. აქედან შეიძლება გრავიტაციული ძალის მანძილზე დამოკიდებულების მიღება. წრიულ ორბიტაზე მოძრაობისას პლანეტაზე მოქმედებს ძალა, რომელიც მზესა და პლანეტას შორის გრავიტაციული ურთიერთქმედებისას აღიძვრება:

\(F\sim \omega ^{2}R=\frac{(2\pi)^{2}R}{T^{2}}.\)

თუ \(T^{2}\sim R^{3}\), მაშინ  \(F\sim \frac{1}{R^{2}}.\)

გრავიტაციული ძალების კონსერვატულობის თვისება პოტენციური ენერგიის ცნების შემოტანის საშუალებას იძლევა. მსოფლიო მიზიდულობის ძალებისათვის მოხერხებულია პოტენციური ენერგიის ათვლა უსასრულოს დაშორებული წერტილიდან დაიწყოს.

გარვიტაციული ძალების მიერ  \(M\)  მასის უძრავი სხეულიდან \(r\)  მანძილზე მდებარე \(m\)  მასის სხეულის მოცემული წერტილიდან გადაადგილებისას, პოტენციური ენერგია შესრულებული მუშაობის ტოლია.

გრავიტაციულ ველში სხეულის პოტენციური ენერგიის გამოთვლის მათემატიკური პროცედურა მცირე გადაადგილებაზე შესრულებული მუშაობების აჯამვაში მდგომარეობს (ნახ. 5).

ნახ. 5.

გრავიტაციულ ველში სხეულის პოტენციური ენერგიის გამოთვლა.

 

მსოფლიო მიზიდულობის კანონი გამოიყენება არ მარტო წერტილოვანი მასის სხეულებისათვის, არამედ სფერულად სიმეტრიული სხეულებისათვისაც,  \(\vec{F}\)  გრავიტაციული  ძალის \(\Delta A_{i}\)  მუშაობა  მცირე გადაადგილებისას \(\Delta \vec{s}_{i}=\Delta \vec{r}_{i}\) ტოლია:

 \(\Delta A_{i}=-G\frac{Mm}{r_{i}^{2}}\Delta r_{i}.\)

როცა \(\Delta r_{i}\rightarrow 0\)  ჯამი ინტეგრალში გადადის. გამოთვლის შედეგად პოტენციური ენერგიისათვის ვღებულობთ:

\(E_{p}=A_{r\infty }=-G\frac{Mm}{r}.\)

სადაც ნიშანი „მინუსი“ ნიშნავს, რომ გარავიტაციული ძალა მიზიდულობის ძალას წარმოადგენს.

თუ სხეული გარავიტაციულ ველში იმყოფება მიზიდულობის ცენტრიდან \(r\) მანძილზე და აქვს რაღაც \(v\) სიჩქარე, მისი სრული მექანიკური ენერგია ტოლია:

\(E=E_{k}+E_{p}=\frac{mv^{2}}{2}-G\frac{Mm}{r}=const.\)

ენერგიის მუდმივობის კანონის თანახმად სხეულის სრული მექანიკური ენერგია გრავიტაციულ ველში მუდმივი რჩება.

სრული ენერგია შეიძლება იყოს დადებითი და უარყოფითი. და ნულის ტოლიც. სრული ენერგიის ნიშანი ციური სხეულის მოძრაობის ხასიათს განსაზღვრავს (ნახ. 6).

როცა  \(E=E_{1}<0\) სხეულს არ შეუძლია მიზიდელობის ცენტრიდან დაშორება \(r>r_{max}\) მანძილზე. ასეთ შემთხვევაში ციური სხეული ელიფსურ ორბიტაზე მოძრაობს (მზის სისტემის პლანეტები, კომეტები).

ნახ. 6.

 \(m\)  მასის სხეულის ენერგიის დიაგრამა, სფერული სიმეტრიის მქონე \(M\) მასისა და \(R\)  რადიუსის სხეულის მიერ შექმნილ, გრავიტაციულ ველში.

 

როცა \(E=E_{2}=0\)  სხეულს შეუძლია უასარულოდ დაშორება. სხეულის სიჩქარე უსასრულიბაში ნულის ტოლი იქნება. სხეული პარაბოლურ ტრაექტორიაზე მოძრაობს. როცა \(E=E_{3}>0\) მოძრაობა ჰიპერბოლურ ტრაექტორიაზე ხდება.  სხეული უსასრულობისკენ მიემართება ენერგიის მარაგით.

კეპლრის კანონები გამოიყენება არა მხოლოს მზის სისტემის პლანეტებისა და სხვა სხეულების მოძრაობისათვის, არამეს დედამიწის ხელოვნული თანამგზავრებისა და კოსმოსური ხომალდების მოძრაობისათვისაც.

პირველ კოსმოსურ სიჩქარეს უწოდებენ თანამგზავრის მოძრაობის სიჩქარეს, რომელიც დედამიწის მახლობელ წრიულ ორბიტაზე მოძრაობს.

\(\frac{mv_{1}^{2}}{R_{3}}=G\frac{Mm}{R_{3}^{2}}=gm,\)

აქედან:

\(v_{1}=\sqrt{G\frac{M}{R_{3}}}=\sqrt{gR_{3}}=7,9\cdot 10^{3}\)  მ/წმ.

მეორე კოსმოსურ სიჩქარეს უწოდებენ მინიმალურ სიჩქარეს, რომელიც უნდა მიანიჭონ კოსმოსურ ხომალდს დედამიწის ზედაპირთან, რომ მან გადალახოს დედამიწის მიზიდულობა, გადაიქცეს მზის ხელოვნურ თანამგზავრად  (ხელოვნურ პლანეტად). ამასთან ხომალდი დედამიწას სცილდება პარაბოლური ტრაექტორიით.

\(E=\frac{mv_{2}^{2}}{2}-G\frac{Mm}{R_{3}}=0,\)

აქადან:

\(v_{2}=\sqrt{2G\frac{M}{R_{3}}}=\sqrt{2gR_{3}}=11,2\cdot 10^{3}\)  მ/წმ.

ნახ. 7–ზე კოსმოსური სიჩქარეების ილუსტრაციაა მოცემული, თუ კოსმოსური ხომალდის სიჩქარე \(v_{1}=7,9\cdot 10^{3}\)  მ/წმ–ს ტოლია და მიმართულება დედამიწის ზედაპირის პარალელურია, მაშინ ხომალდი  დედამიწის ზედაპირიდან მცირე სიმაღლეზე წრიულ ორბიტაზე იმოძრავებს. როცა საწყისი სიჩქარე \(v_{1}\)–ს აღემატება, მაგრამ ნაკლებია \(v_{2}=11,2\cdot 10^{3}\)  მ/წმ–ზე, ხომალდის ორბიტა ელიფსურია.  \(v_{2}\)–ის ტოლი საწყისი სიჩქარის დროს ხომალდი პარაბოლაზე მოძრაობს, უფრო დიდ სიჩქარეებზე კი – ჰიპერბოლაზე.

ნახ. 7.

კოსმოსური სიჩქარეები.მითითებულიადედამიწის ზედაპირის მახლობელი  სიჩქარეები. 1: \(v=v_{1}\) – წრიული ტრაექტორია; 2: \(v_{1}<v<v_{2}\) – ელიფსური ტრაექტორია; 3:\(v=11,1\cdot 10^{3}\) м/с – ძლიერად გაჭიმული ელიფსი; 4: \(v=v_{2}\)  – პარაბოლურიტრაექტორია 5: \(v>v_{2}\)  – ჰიპერბოლური ტრაექტორია; 6: მთვარის ტრაექტორია.

{loadnavigation}

მცირე პლანეტა, ერთ-ერთი უდიდესი (საშუალო დიამეტრი 525 კმ, მასა 2,6*1020კგ) ასტეროიდ ვესტას ბრუნვა გადაღებული კოსმოსური ხომალდიდან. ვესტას ბრუნვის პერიოდია 5.342 საათი.

 

მყარი სხეულის ბრუნვის კინემატიკის აღსაწერად მოსახერხებელია კუთხური სიდიდეები: კუთხური გადაადგილება \(\Delta \varphi\),  კუთხური სიჩქარე \(\omega\).

\(\omega =\frac{\Delta \varphi }{\Delta t}; (\Delta t\rightarrow 0)\),

და კუთხური აჩქარება \(\varepsilon \);

\(\varepsilon =\frac{\Delta\omega }{\Delta t}; (\Delta t \rightarrow 0).\)

ამ ფორმულებში კუთხე გამოისახება რადიანებით. მყარი სხეულების ბრუნვისას უძრავი ღერძის გარშემო, მის მიმართ სხეულის ყველა წერტილი მოძრაობს ერთნაირი კუთხური სიჩქარითა და ერთნაირი კუთხური აჩქარებით. ბრუნვის დადებით მიმართულებად მიჩნეულია საათის ისრის მოძრაობის საწინააღმდეგო მიმართულება.

ნახ.1. დისკოს ბრუნვა O წერტილში მართობულად გამავალი ღერძის მიმართ

 

\(\Delta m\) მასის სხეულის მცირე გადაადგილებისას კუთხური გადაადგილების \(\Delta \varphi \) და \(\Delta \vec{s}\) წრფივი გადაადგილების ვექტორის მოდულს შორის კავშირი გამოისახება შემდეგნაირად:

\(\Delta \vec{s}=r\Delta \varphi \),

სადაც \(r\) -\(\vec{r}\)  რადიუსის ვექტორის მოდულია (ნახ.1). აქედან გამომდინარეობს კავშირი წრფივი და კუთხური სიჩქარეების მოდულებს შორის:

\(v=\omega r\),

და კავშირი წრფივი და კუთხური აჩქარებების მოდულებს შორის:

\(a=a\iota =r\varepsilon \).

ვექტორები \(\vec{v}\) და \(\vec{a}=\vec{a}_{\iota }\) მიმართულია \(r\) რადიუსიანი წრეწირის გასწვრივ. გავიხსენოთ ასევე მრუდწირული მოძრაობისას აღიძვრება ცენტრისკენული აჩქარებაც, რომლის მოდული ტოლია:

\(a_{n}=\frac{v^{2}}{r}=\omega ^{2}r\).

მბრუნავი სხეული დავანაწილოთ მცირე \(\Delta m_{i}\) მასის ნაწილებად, ბრუნვის ღერძამდე მანძილი ავღნიშნოთ \(r_{i}\)- თი, ხოლო წრფივი სიჩქარის მოდული ავღნიშნოთ \(v_{i}\)-თი. მაშინ მრუნავი სხეულის კინეტიკური ენერგია შეიძლება დავწეროთ შემდეგნაირად:

\(E_{k}=\sum_{i}\frac{\Delta mv_{i}^{2}}{2}=\sum_{i}\frac{\Delta m(r_{i}\omega )^{2}}{2}=\frac{\omega ^{2}}{2}\sum_{i}\Delta m_{i}r_{i}^{2}\)

ფიზიკურ სიდიდე \(\sum_{i}\Delta m_{i}r_{i}^{2}\) -ს ეწოდება სხეულის ინერციის მომენტი და აღინიშნება \(I\)-თი:

\(I=\sum_{i}\Delta m_{i}r_{i}^{2}\)

\(\Delta m \to 0\) ზღვარში ეს ჯამი გადადის ინტეგრალში. ინერციის მომენტის ერთეული \(Si\)–ში არის კილოგრამი მეტრ კვადრატი (კგ*მ²). ამგვარად, უძრავი ღერძის მიმართ მბრუნავი სხეულის კინეტიკური ენერგია შეიძლება წარმოვადგინოთ შემდეგი სახით:

\(E_{k}=\frac{I\omega ^{2}}{2}\)

ეს ფორმულა ძალიან გავს წრიფავად მოძრავი სხეულის კინეტიკური ენერგიის გამოსათვლელ ფორმულას \(\frac{mv^{2}}{2}\), უბრალოდ აქ მასის მაგივრად ინერციის მომენტია და წრიფივი სიჩქარის მაგივრად კუთხური სიჩქარე.

ბრუნვითი მოძრაობის დინამიკაში ინერციის მომენტი იგივე როლს ასრულებს, რასაც მასა მოძრავი სხეულის დინამიკაში. მაგრამ არსებობს პრინციპული განსხვავება: თუ მასა დამოკიდებული არ არის სხეულის მოძრაობაზე, ინერციის მომენტი დამოკიდებულია იმაზე, თუ რომელი ღერძის გარშემო ბრუნავს სხეული. სხვადასხვა ბრუნვის ღერძებისადმი ერთიდაიგივე სხეულების ინერციის მომენტები განსხვავებულია. ბევრ ამოცანაში განიხილება შემთხვევა, როდესაც მყარი სხეულის ბრუნვის ღერძი გადის ამ სხეულის მასათა ცენტრში. ისეთი სისტემის მასათა ცენტრი, რომელიც შედგება \(m_{1}\) და \(m_{2}\) მასებისგან. რომელთაგან თითოეულის კოორდინატებია \(x_{1}\), \(y_{1}\) და  \(x_{2}\), \(y_{2}\)  (ნახ.2), განისაზღვრება ფორმულებით:

\(x_{c}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}\);        \(y_{c}=\frac{m_{1}y_{1}+m_{2}y_{2}}{m_{1}+m_{2}}\).

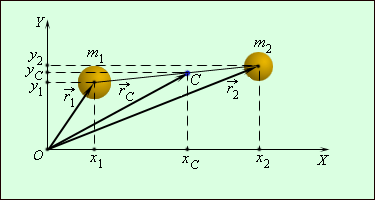
(ნახ.2) ორი ნაწილისაგან შემდგარი სისტემის მასათა ცენტრი.

 

ვექტორულ ფორმაში ეს გამოსახულებები მიიღებს შემდეგ სახეს:

\(r_{c}=\frac{m_{1}\vec{r}_{1}+m_{2}\vec{r}_{2}}{m_{1}+m_{2}}\)

ანალოგიურად ბევრი ნაწილაკებისგან შემდგარი სისტემისთვის მასათა ცენტრის რადიუს ვექტორი\(\vec{r}_{c}\)  განისაღვრება შემდეგი გამოსახულებით:

\(\vec{r}_{c}=\frac{\sum m_{i}\vec{r_{i}}}{\sum m_{i}}\)

რთული ფორმის სხეულის მასათა ცენტრის გამოსათვლელად \(\vec{r}_{c}\) ფორმულა იცვლება ინტეგრალებით. ადვილი დასანახია, რომ ერთგვაროვანი სიმძიმის ველის მოქმედებისას სხეულის მასათა ცენტრი შეესაბამება სხეულის სიმძიმის ცენტრს. ამოტომ რთული ფორმის სხეულის მასათა ცენტრის განსაზღვრა შეიძლება შემდეგი გზით: მიმდევრობით დავკიდოთ სხეული სხვადასხვა ადგილით და გავატაროთ საკიდის მართობული წრფეები.(სურ.3)

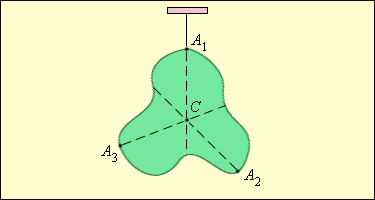
(სურ. 3) რთული ფორმის სხეულის მასათა ცენტრის განსაზღვრა A₁, A₂, A₃ წერტილებზე ჩამოკიდებით.

თუ სხეული ჩამოკიდებულია მასათა ცენტრით მაშინ იგი იმყოფება განურჩეველ წონასწორობაში. ნებისმიერი მოძრაობა შეიძლება დავშალოთ ორ მოძრაობად: მასათა ცენტრის სიჩქარით გადატანით მოძრაობად და ბრუნვად მასათა ცენტრზე გამავალი ღერძის მიმართ. მაგალითად შეიძლება გამოდგეს ბორბალი, რომელიც ბრუნავს სრიალის გარეშე. ბორბლის ბრუნვისას მისი ყველა წერტილი ბრუნავს ნახატის სიბრტყის პარალელულ სიბრტყეში.

ასეთ მოძრაობას სიბტყული მოძრაობა ეწოდება. სიბრტყული მოძრაობისას მყარი სხეულის კინეტიკური ენერგია ტოლია გადატანითი მოძრაობის კინეტიკური ენერგიისა და სხეულის ბრუნვის კინტიკური ენერგიის ჯამის, რომელიც ბრუნავს იმ ღერძის მიმართ რომელიც გადის ამ სხეულის მასათა ცენტრზე და მართობულია იმ სიბრტყისა, რომელშიც მოძრაობს ამ სხეულის წერტილები:

\(E_{k}=\frac{mv_{c}^{2}}{2}+\frac{I_{c}\omega ^{2}}{2}\)

სადაც \(m\)– მთელი სხეულის მასაა, ხოლო I_C– სხეულის ინერციის მომენტია, მის მასათა ცენტრზე გამავალი ღერძის მიმართ.

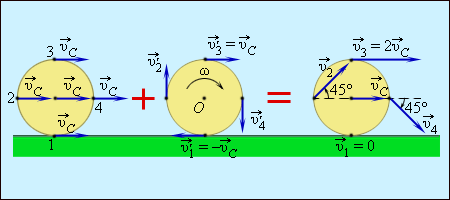
სურ. 4. ბორბლის ბრუნვა როგორც გადატანითი მოძრაობისა \(\vec{v}_{c}{tex} და {tex}\omega =\frac{v_{c}}{R}\) კუთხური სიჩქარით მოძრაობის ჯამი.

 

მექნიკაში მტკიცდება შემდეგი თეორემა მასათა ცენტრის მოძრაობის შესახებ: სხეულის ან ურთიერთმოქმედ სხეულთა სისტემის მასათა ცენტრზე გარე ძალის მოქმედებისას, მასათა ცენტრი მოძრაობს როგორც მატერიალური წერტილი, რომელშიც განაწილებულია მთელი სხეულის მასა. ამ პროცესს კარგად ასახავს ქვემოთ მოცემული სურათი (სურ. 5) სურათზე გამოსახულია სხეულის მოძრაობა, რომელზეც მოქმედებს სიმძიმის ძალა. სხეულის მასათა ცენტრი მოძრაობს პარაბოლაზე, როგორც მატერიალური წერტილი, მაშინ როცა ყველა დანარჩენი წერტილი უფრო რთულ ტრაექტორიებზე მოძრაობენ.

(სურ. 5) მყარი სხეულის მოძრაობა სიმძიმის ძალის მოქმედების ქვეშ.

 

თუ მყარი სხეული ბრუნავს რომელიმე უძრავი ღერძის მიმართ, მაშინ მისი ინერციის მომენტი \(I\) შეიძლება გამოისახოს ამ სხეულის \(I_{c}\)  ინერციის მომენტით მის მასათა ცენტრზე გამავალი ღერძის მიმართ, რომელიც პარალელურია პირველი ღერძისა.

სურ. 6. ბრუნვის ღერძის პარალელურად გადატანის შესახებ თეორემის დამტკიცება.

 

განვიხილოთ ნებისმიერი ფორმის მყარი სხეული (სურ. 6). \(XOY\) კოორდინატთა სისტემის სათავედ ავირჩიოთ \(O\) წერტილი, რომელიც ემთხვევა სხეულის მასათა \(C\) ცენტრს. დავუშვათ ერთ-ერთი ბრუნვის ღერძი გადის მასათა ცენტრში ხოლო მეორე– ნებისმიერ \(P\) წერტილში რიმელიც \(C\)–სგან \(d\) მანძილითაა დაშორებული. ორივე ღერძი ნახაზის პერპენდიკულარულია. დავუშვათ \(\Delta m_{i}\)–მყარი სხეულის მასის რაღაც მცირე ელემენტია. ინერციის მომენტის განსაზრვრების თანახმად:

\(I_{c}=\sum \Delta m_{i}(x_{1}^{2}+y_{1}^{2})\),

\(I_{P}=\sum \Delta m_{i}\left | (x_{i}-a)^{2}+(y_{i}-b)^{2} \right |\)

გამოსახულება\(I_{P}\)–სთვის შეიძლება გარდავქმნათ შემდეგნაირად:

\(I_{P}=\sum \Delta m_{i}(x_{1}^{2}+y_{1}^{2})+\sum \Delta m_{i}(a^{2}-b^{2})-2a\sum \Delta m_{i}x_{i}-2b\sum \Delta m_{i}y_{i}\)

რადგან კოორდინატთა სათავე ემთხვევა მასათა ცენტრს, ბოლო ორი წევრი 0 ის ტოლი გამოდის. ეს გამომდიმარეობს მასათა ცენტრის განსაზღვრიდან. საყურადღებოა, რომ

\(I_{P}=I_{C}+md_{2}\),

სადაც m – მთლიანი სხეულის მასაა. ამ შედეგს ეწოდება შტაინერის თეორემა (თეორემა ბრუნვის ღერძის პარალელური გადატანის შესახებ). 

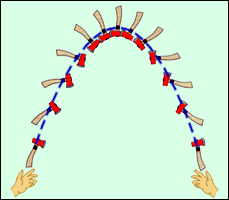
ნიუტონის მეორე კანონი შეიძლება განვაზოგადოთ მყარი სხეულის ბრუნვაზე უძრავი ღერძის მიმართ. სურ. 8– ზე გამოსახულია რომელიღაც მყარი სხეული, რომელიც ბრუნავს \(O\) წერტილზე გამავალ ნახატის პერპენდიკულარულ ღერძის მიმართ. გამოვყოთ ნებისმიერი მცირე ელემენტი \(\Delta m_{i}\)  მასით. მასზე მოქმედებს შიგა და გარე ძალები. ყველა ძალის ტოლქმედია \(\vec{F}_{i}\) ის შეიძლება დავშალოთ ორ მაბრუნებელ \(\vec{F}_{i\tau }\) და რადიანულ \(\vec{F}_{ir}\) მდგენელად. რადიანული მდგენელი \(\vec{F}_{ir}\) ქმნის ცენტისკენულ აჩქარება \(a_{n}\)–ს.

(სურ. 7) მაბრუნებელი \(\vec{F}_{i\tau }\) და რადიანული \(\vec{F}_{ir}\) ,რომლებიც მოქმედებენ ელემენტ \(\Delta m_{i}\)_–ზე და ადგენს ძალა \(\vec{F}_{i}\)–ს.

 

\(\vec{F}_{i\tau }\) მდგენელი იწვევს \(\Delta m_{i}\) მასის ტანგენციალურ \(\vec{a}_{i\tau }\) აჩქარებას. ნიუტონის მეორე კანონს სკალარულ ფორმაში ექნება შემდეგი სახე:

\(\Delta m_{i}a_{i\tau}=F_{i\tau}=F_{i}\sin \theta\), ან \(\Delta m_{i}r_{i}\varepsilon=F_{i}\sin \theta\)

სადაც \(\varepsilon =\frac{a_{i\tau}}{r_{i}}\)– მთელი სხეულის კუთხური აჩქარებაა. თუ განტოლების ორივე მხარეს გავამრავლებთ \(r_{i}\) –ზე, მივიღებთ:

\(\Delta m_{i}r_{i}^{2}\varepsilon =F_{i}r_{i}\sin \theta =F_{i}l_{i}=M_{i}\)

სადაც \(l_{i}\)– \(\vec{F}_{i}\) ძალის მხარია, ხოლო \(M_{i}\) – ძალის მომენტი.

ეხლა საჭიროა იგივე შეთანხმებები დავწეროთ ყველა \(\Delta m_{i}\) ელემენტისთვის და შემდეგ ავჯამოთ მარჯვენა და მარცხენა მხარეები. ეს მოგვცემს:

\(\sum \Delta m_{i}r_{i}^{2}\varepsilon =\sum M_{i}\)

მარჯვენა მხარე სხვადასხვა წერტილზე მოქმედი ძალის მომენტების ჯამია, რომელიც შედგება ყველა გარე ძალის მომენტებისგან და ყველა შინაგანი ძალის მომენტების ჯამისგან.

\(\sum M_{i}=\sum (M_{i_{garegani}})+\sum (M_{i_{shinagani}})\)

მაგრამ ნიუტონის მეორე კანონის თანახმად ყველა შინაგანი ძალის მომენტების ჯამი 0–ის ტოლია, ამიტომ მარჯვენა მხარე დარჩება მხოლოდ გარე ძალების მომენტების ჯამი , რომელსაც ავღნიშნავთ \(M\)–ით. ანუ:

\(I\varepsilon =M\).

ეს კი მყარი სხეულის ბრუნვის დინამიკის მთავარი განტოლებაა. კუთხური აჩქარება \(\varepsilon\) და ძალის მომენტი \(M\), ამ ფორმულაში ალგებრული სიდიდეებია. ძირითადად სხეულის ბრუნვის დადებით მიმართულებად მიჩნეულია, საათის ისრის ბრუნვის საწინააღმდეგო მიმართულება.

გადატანითი მოძრაობის შესწავლის დროს  შემოვიტანეთ ცნება სხეულის იმპულსის შესახებ \(\vec{p}\). ანალოგიურად სხეულის ბრუნვის დინამიკის შესწავლისას შემოგვაქვს იმპულსის მომენტი.

იმპულსის მომენტი ეწოდება ფიზიკურ სიდიდეს, რომელიც ტოლია სხეულის ინერციის მომენტის \(I​\)  და სხეულის ბრუნვის კუთხური სიჩქარის \(\omega\)  ნამრავლის. იმპულსის მომენტი აღინიშნება \(L​\) ასოთი და ტოლია:

\(L=I\omega\)

რმდენადაც \(\varepsilon =\frac{\Delta \omega }{\Delta t}; (\Delta tn \to 0),\) ბრუნვითი მოძრაობის განტოლება შეიძლება წარმოვადგინოთ შემდეგი სახით:

\(M=I\varepsilon =I\frac{\Delta \omega }{\Delta t}\) ან \(M\Delta t=I\Delta \omega =\Delta L.}\)

საბოლოოდ მივიღებთ:

\(M=\frac{\Delta L}{\Delta t}; (\Delta tn \to 0).\)

ეს განტოლება მიღებულია იმ შემთხვევისთვის თუ \(I=const\), მაგრამ სამრთლიანი ზოგადი შემთხვევისთვისაც, თუ ბრუნვის დროს სხეულის ინერციის მომენტი იცვლება.

 

თუ გარე ძალების ჯამური მომენტი \(M\) ნულის ტოლია, მაშინ იმპულსის მომენტი \(L=I\omega\) მოცემული ღერძის მიმართ ინახება:

\(\Delta L=0,\) თუ \(M=0\)

ესე იგი,

\(L=I\omega =const.\)

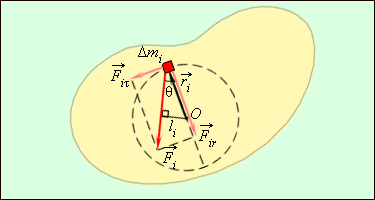
სწორედ ეს არის იმპულსის მუდმივობის კანონი.  ამ კანონის საილუსტრაციოდ გამოდგება (სურ. 8), სადაც ასახულია ორი ერთ ღერძზე ჩამოცმული არადრეკადი მბრუნავი დისკოს დაჯახება.

(სურ.8) ორი არადრეკადი დისკოს დაჯახება. იმპულსის მუდმივობის კანონი: \(I_{1}\omega_{1}=(I_{1}+I_{2})\omega\)

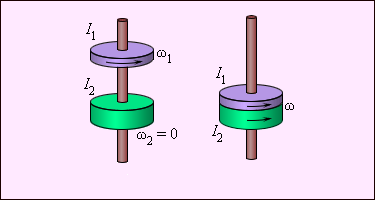
იმპულსის მუდმივობის კანონი სამართლიანი ნებისმიერი ჩაკეტილი სისტემისთვის. სხეულის ბრუნვის დინამიკის ძირითადი კანონი მოქმედებს თანაბრადაჩქარებული სხეულის მოძრაობის დროსაც. ამის მაგალითად შეიძლება გამოდგეს სხეულის (რკალის, ცილინდრის, ბურთის) გორვა დახრილ სიბრტყეზე. (სურ. 9)

ნახ. 9

ბრუნვის ღერძი გადის სხეულის მასათა ცენტრში. ბრუნვის ღერძის მიმართ სიმძიმის ძალის \(m\vec{g}\) და რეაქციის ძალის \(\vec{N}\) მომენტები 0–ის ტოლია. მომენტს ქმნის მხოლოდ ხახუნის ძალა.

სხეულის ბრუნვის განტოლება:

\(I_{C}\varepsilon =I_{C}\frac{a}{R}=M=F_{\texttt{xax}}R,\)

სადაც \(\varepsilon\) – მბრუნავი სხეულის კუთხური აჩქარებაა, \(a\) – მისი ცენტრის წრფივი აჩქარება, ხოლო \(I_{C}\) – სხეულის ინერციის მომენტი მისი ცენტრის მიმართ.

ნიუტონის მეორე კანონი შემდეგნაირად ჩაიწერება:

\(ma=mg\sin \alpha -F_{\texttt{xax}}\)

დუ გამოვსახავთ ამ განტოლებებიდან \(F_{\texttt{xax}}\)–ს და გავუტოლებთ ერთმანეთს მივიღებთ:

\(a=\frac{mg\sin \theta }{(\frac{I_{C}}{R^{2}}+m)}.\)

მაგალითად ბურთისთვის \(I_{C}=\frac{2}{5}mR^{2},\) და ცილინდრისთვის \(I_{C}=\frac{1}{2}mR^{2},\) საყურადღებოა რომ ბურთი იგორებს ცილინდრზე სწრაფად.

{loadnavigation}

სითხეებისა და აირების მოძრაობა რთულ მოვლენას წარმოადგენს. მისი აღწერისათვის სხვადასხვა გამარტივებული დაშვება (მოდელი) გამოიყენება. უმარტივეს მოდელში, სითხე (და აირიც კი) უკუმშვადად და იდეალურადაა (ე.ი.მოძრაობისას ფენებს შორის შინაგანი ხახუნი არ არის) მიღებული. იდეალური სითხის მოძრაობისას მექანიკური ენერგიის შინაგან ენერგიად გარდაქმნა არ ხდება, ამიტომ ადგილი აქვს მექანიკური ენერგიის მუდმივობის კანონს. ამ კანონის შედეგს, იდეალური და უკუმშვადი სითხის სტაციონალური ნაკადისათვის, 1738 წელს ჩამოყალიბებული ბერნულის განტოლება წარმოადგენს. სტაციონალურად უწოდებენ ისეთი სითხის ნაკადს, რომელშიც გრიგლები არ წარმოიქმნება.  სტაციონალურ ნაკადში სითხის ნაწილაკები გადაადგილდებიან დროში უცვლელი ტრაექტორიებით, რომელთაც დენის წირები ეწოდებათ. გამოცდილება გვიჩვენებს, რომ სტაციონალური ნაკადები მხოლოდ სითხის მცირე სიჩქარით მოძრაობისას წარმოიქმნება.

 

განვიხილოდ იდეალური   და უკუმშვადი სითხის სტაციონალური ნაკადის მოძრაობა ცვლადი განივკვეთის მილში (ნახ. 1). მილის სხვადასხვა ნაწილები სხვადასხვა სიმაღლეზე შეიძლება იყოს განლაგებული.

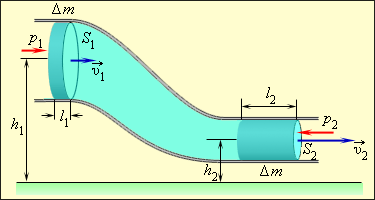
ნახ. 1.

ცვლადი განივკვეთის მილში იდეალური სითხის დენა.

 \(\Delta V_{1}=l_{1}S_{1}; \Delta V_{2}=l_{2}S_{2}\).

უკუმშვადობის პირობა: \(\Delta V_{1}=\Delta V_{2}=\Delta V\) დროის \(\Delta t\) მონაკვეთში  \(S_{1}\) განივკვეთის მილში სითხე გადანაცვლდება \(l_{1}=u_{1}\Delta t\) –ზე, ხოლო \(S_{2}\) განივკვეთის მილში –  \(l_{2}=u_{2}\Delta t\) –ზე, სადაც \(v_{1}\) და \(v_{2}\) – მილში სითხის ნაწილაკების სიჩქარეა. უკუმშვადობის პირობა  ჩაიწერება შემდეგი სახით: 

\(\Delta V=l_{1}S_{1}=l_{2}S_{2}\)    ან    \(v_{1}S_{1}=v_{2}S_{2}\) .

სადაც \(\Delta V\) – \(S_{1}\) და \(S_{2}\) –ში გამდინარე სითხის მოცულობაა.

ამგვარად, სითხის, დიდი განივკვეთის მქონე მილიდან ნაკლები განივკვეთის მილში, გადასვლისას დინების სიჩქარე იზრდება, ე.ი. სითხე აჩქარებულად მოძრაობს. აქედან გამომდინარე, სითხეზე ძალა მოქმედებს. ჰორიზონტულ მილში ეს ძალა მხოლოდ ფართო და ვიწრო მილებში  წნევათა სხნაობის გამო შეიძლება აღიძრას. თუ მილის ეს მონაკვეთები სხვადასხვა დონეზე მდებარეობენ, მაშინ აჩქარება გამოწვეულია  წნევისა და სიმძიმის ძალების ერთდროული მოქმედებით. წნევის ძალა – სითხის შეკუმშვის დრეკადობის ძალაა. სითხის უკუმშვადობა მხოლოდ იმას ნიშნავს, რომ დრეკადობის ძალები თავს იჩენს მხოლოდ სითხის ნებისმიერი ნაწილის მოცულობის იმდენად მცირე ცვლილევისას, რომ მისი უგულვებელყოფა შეიძლება.

რადგან სითხე იდეალურადაა ჩათვლილი, ის მილში ხახუნის გარეშე მიედინება. ამიტომ მის დინებასთან შეიძლება მექანილური ენერგიის მუდმივობის კანონის მიყენება.

სითხის გადაადგილებისას წნევის ძალები ასრულებენ მუშაობას:

\(\Delta A=p_{1}S_{1}l_{1}-p_{2}S_{2}l_{2}=p_{1}S_{1}v_{1}\Delta t-p_{2}S_{2}v_{2}\Delta t=(p_1-p_{2})\Delta V.\) 

წნევის ძალების მუშაობა ΔA სითხის დრეკადი დეფორმაციის პოტენციური ენერგიის ცვლილების ტოლია საწინააღმდეგო ნიშნით.

დროის საწყისი მომენტიდან \(S_{1}\) და \(S_{2}\) შორის მოქცეულ სითხეში \(\Delta t\) დროის განმავლობაში მომხდარი ცვლილებები, სტაციონალური დინებისას დაიყვანება  \(m=\rho \Delta V\) (\(\rho\) – სითხის სიმკვრივეა) მასის სითხის  მილის ერთი  \(S_{1}\) განივკვეთის მქონე ნაწილიდან მეორე \(S_{2}\) განივკვეთის მქონე ნაწილში გადაადგილებამდე (ნახ. 1–ზე დაშტრიხული მოცულიბა). ამ მასისათვის მექანიკური ენერგიის შენახვის კანონს აქვს სახე:

\(E_{2}-E_{1}=\Delta A=(p_{1}-p_{2})\Delta V,\) 

სადაც \(E_{1}\) და \(E_{2}\) –  მიზიდულობის ველში \(\Delta m\) მასის სრული მექანიკური ენერგიაა:

\(E_{1}=\frac{\Delta mv_{1}^{2}}{2}+\Delta mgh_{1}; E_{2}=\frac{mv_{2}^{2}}{2}+\Delta mgh_{2}.\) 

აქედან გამოდის:

\(\frac{\rho v_{1}^{2}}{2}+\rho gh_{1}+p_{1}=\frac{\rho v_{2}^{2}}{2}+\rho gh_{2}+p_{2}.\) 

სწორედ ეს არის ბერნულის განტოლება. აქედან გამოდის, რომ ჯამი მილის მთელი სიგრძის გასწვრივ მუდმივი რჩება:

\(\frac{\rho v^{2}}{2}+\rho gh+p=const.\)

კერძოდ, ჰორიზონტულად განლაგებული მილისათვის  (\(h_{1}=h_{2}\)  ბერნულის განტოლებას აქვს სახე:

\(\frac{\rho v^{2}}{2}+p=const.\) 

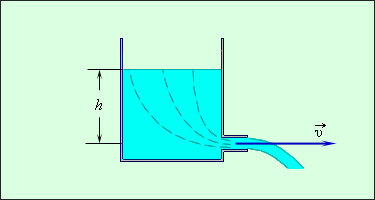
\(P\) სიდიდე – სითხეში სტატიკური წნევაა. ის შეიძლება სითხესთან ერთად მოძრავი მონომეტრის საშუალებით გაიზომოს. პრაქტიკულად წნევა, მილის სხვადასხვა განივკვეთში იზომება მონომეტრული მილების საშუალებით როგორც ნახ. 2–ზეა  ნაჩვენები. ბერნულის განტოლებიდან გამოდის, რომ:

ცვლადი განივკვეთის მქონე ჰორიზონტულ მილში გამდინარე სითხის წნევა იმ კვეთაშია მეტი, სადაც მოძრაობის (დინების) სიჩქარე ნაკლებია, და პირიქით, წნევა ისეთ კვეთაშია ნაკლები, სადავ სიჩქარე მეტია.

ნახ. 2.

სითხეში წნევის გაზომვა მონომეტრების საშუალებით. \(v_{1}<v_{2}<v_{3};\: h_{1}>h_{2}>h_{3}\) 

თუ სითხის ნაკადის კვეთა საკმარისად დიდია, ბერნულის განტოლება უნდა გამოვიყენით დენის წირებისათვის, ე.ი. წირებისათვის რომლის გასწვრივაც გადაადგილდება სითხის ნაწილაკები სტაციონალურო დინებისას. მაგალითად, იდეალირი უკუმშავადი სითხის განიერი ჭურჭლის გვერდითი კედლის  ან ფსკერის ნახვრეტიდან გამოდინებისას, დენის წირები იწყებიან ჭურჭლის ზედაპირთან და გადიან ნახვრეტში (ნახ. 3).

ნახ. 3,

სითხის გამოდინება განიერი ჭურჭლიდან

რადგან, ჭურჭლის ზედაპირთან  სითხის სიჩქარის უგულვებელოფა შეიძლება მისი სიმცირის გამო, ბერნულის განტოლება იღებს სახეს:

\(\rho gh+p_{0}=\frac{\rho v^{2}}{2}+p_{0},\) 

სადაც \(p_0\) – ატმოსფეროლი წნევაა, \(h\) – სითხის დინების მიმართ დონეთა სხვაობაა. ამგვარად,

\(v=\sqrt{2gh}.\) 

გამოდინების სიჩქარის ამ გამოსახულებას ტორიჩელის ფორმულას უწოდებენ. იდეალური სითხის ჭურჭლის ხვრელიდან გამოდინების სიჩქარე ისეთივეა როგორიც \(h\) სიმაღლიდან უსაწყისო სიჩქარით ვარდნილი სხეულის სიჩქარე.

სითხეებისაგან განსხვავებით აირებს შეუძლიათ მოცულებების მნიშვნელოვანი ცვილება. გათვლები უჩვენებენ, რომ აირების კუმშვადობის უგულვებელყოფა შესაძლებელია, თუ აირის ნაკადის უდიდესი სიჩქარე ნაკლებია, ამ აირში ბგერის გავრცელების სიჩქარეზე. ასეთ პირობებში, ბერნულის განტოლება  აეროდინამიკის ამოცანების ფართო კლასისათვის შეიძლება იქნეს გამოყენებული.

  

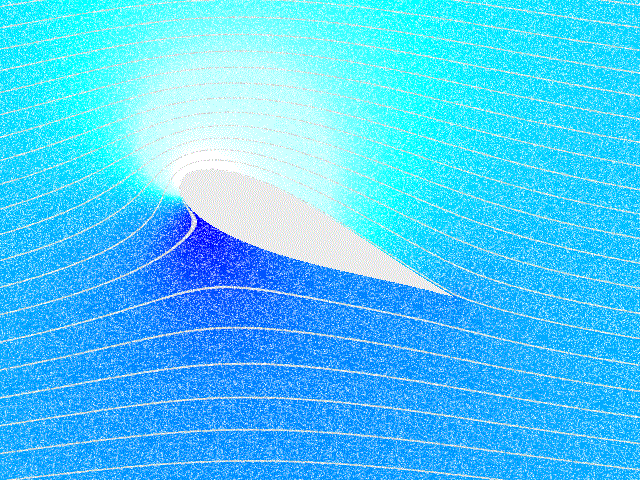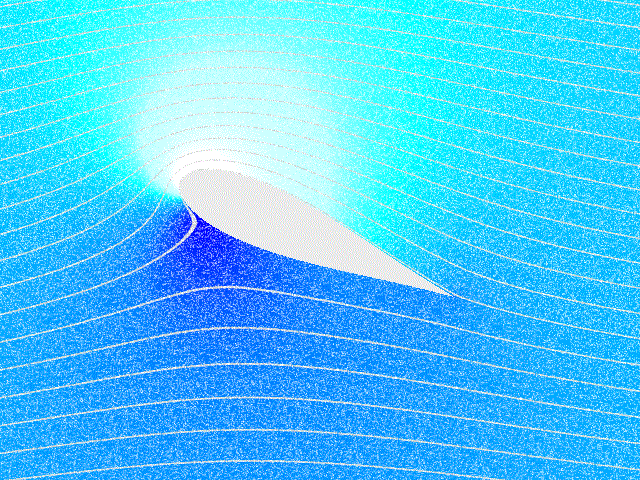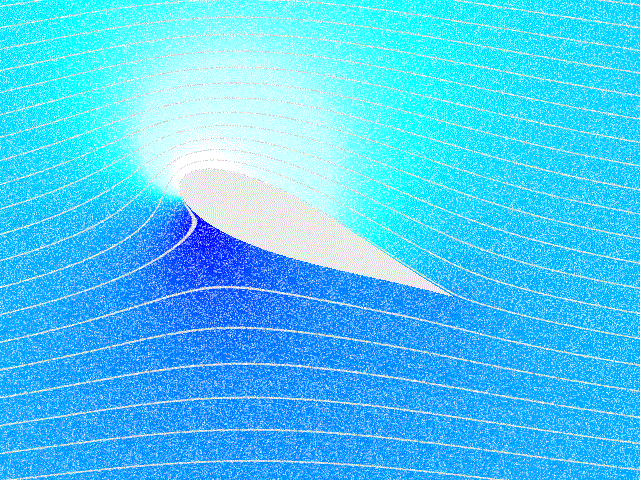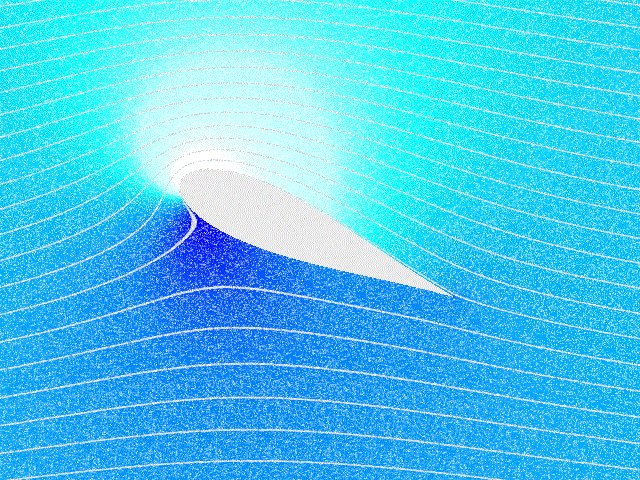
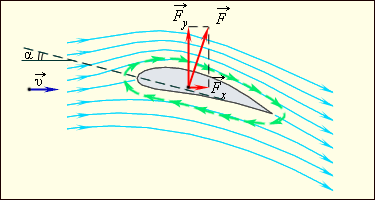
ერთ–ერთი ასეთი ამოცანაა თვითმფრინავის ფრთაზე მოქმედი ძალების შესწავლა. ამ ამოცანის მკაცრი თეორიული ამოხსნა ძალიან რთულია და ჩვეულებრივ, ძალების კვლევისათვის ექსპერიმენტულ მეთოდებს იყენებენ. ბერნულის განტოლება ფრთის ამწევი ძალის წარმოქმნის მხოლოდ რაოდენობრივი ახსნის საშუალებას იძლევა. ნახ. 4–ზე გამოსახულია თვითმფრინავის ფრთის გარსმდენი ჰაერის ნაკადის დინების წირები. ფრთის სპეციალური ფორმის და დაჯახების (ჰაერის დარტყმის) კუთხის, ე.ი. ფრთის დახრასა და მასზე დაცემული ჰაერის ნაკადს შორის კუთხის გამო ფრთის ზევით ჰაერის ნაკადის სიჩქარე უფრო მეტია ვიდრე ფრთის ქვევით. ამიტომ ნახ. 4–ზე დინების წირები ფრთის ზევით უფრო მჭიდროდაა (ახლო–ახლოა ერთმანეთთან) განლაგებული, ვიდრე ფრთის ქვევით. ბერნულის განტოლებიდან გამოდის, ფრთის ქვევით წნევა იქნება მეტი, ვიდრე ზევით; რის შედეგადაც აღიძვრება ფრთაზე მოქმედი ძალა \(\vec{F},\)  ამ ძალის ვერტიკალურ მდგენელს \(\vec{F}_{y}\) tამწევ ძალას უწოდებენ. ამწევი ძალა თვითმფრინავზე მოქმედი სიმძიმის ძალის კომპენსირების საშუალებას იძლევა და ამის მეშვეობით ჰაერში მძიმე საფრენი აპარატების ფრენაა შესაძლებელი. ჰორიზონტული მდგენელი \(\vec{F}_{x}\) გარემოს წინააღმდეგობის მდგენელს წარმოადგენს.

ნახ. 4.

თვითმფრინავის ფრთის გასმდენი ჰაერის  ნაკადის დინების წირები და ამწევი ძალის წარმოქმნა. \(\alpha\) –  დაჯახების კუთხე.

 

ფრთის ამწევი ძალის თეორიის მიხედვით ფრთის გარსშემოდინების დროს მნიშვნელოვან როლს ასრულებს ზედაპირულ ფენებში აღძრული სველი ხახუნის ძალები. მათი მოქმედების შედეგად ფრთის გარშემო აღიძვრება ჰაერის წრიული მოძრაობა (ცირკულაცია) (ნახ. 4–ზე მწვანე ისრები). ფრთის ზედა მაწილში ცირკულირებადი ჰაერის სიჩქარე იკრიბება ფრთაზე დაცემული ნაკადის სიჩქარესთან, ქვედა ნაწილში კი სიჩქარეები ურთიერთსაწინააღმდეგოდაა მიმართული. სწორედ ეს იწვევს წნევათა სხვაობას და ამწევი ძალის წარმოქმნას.

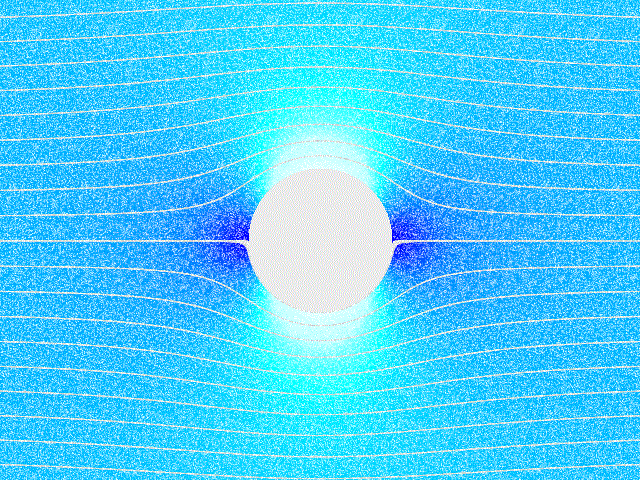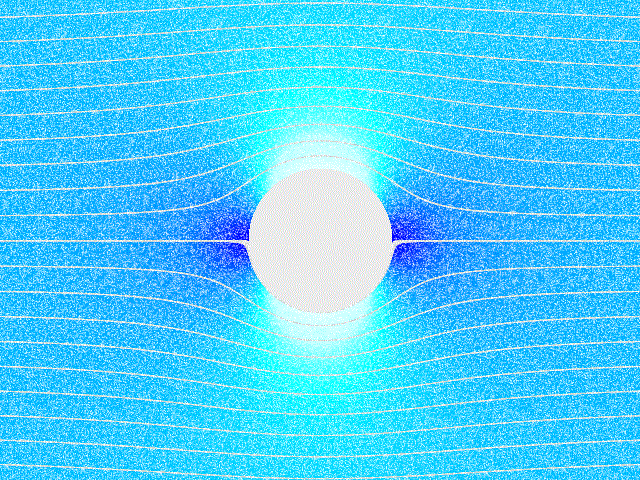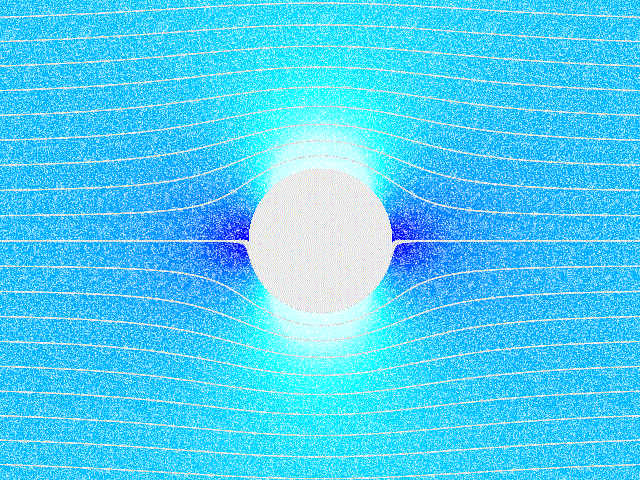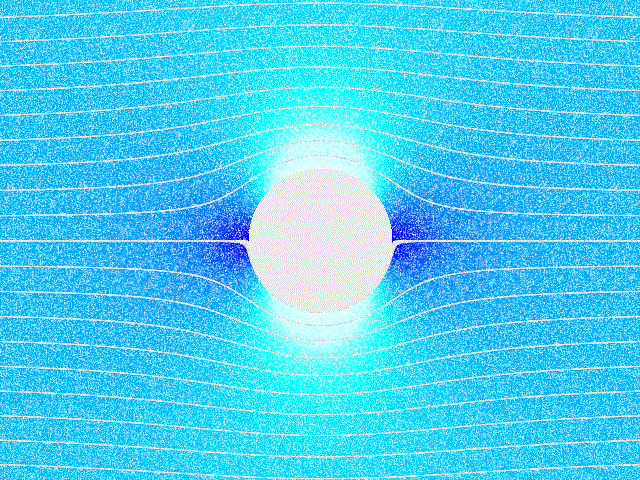
სველი ხახუნით გამოწვეული ჰაერის ცირკულაცია მბრუნავი სხეულის (მაგ. ცილინრის) გარშემოც აღიძვრება. ბრუნვისას, ცილინდრი აიყოლიებს გარშემო მყოფ ჰაერის ფენებს და  მათ ცირკულირებას იწვევს. თუ ასეთ ცილინდრს მოვათავსებთ ჰაერის ნაკადში, წარმოიქმნება, თვითმფრინავის ფრთის ამწევი ძალი ანალოგიური, გვერდითი წნევის ძალა. ამ მოვლენას მაგნუსის ეფექტს უწოდებენ. ნახ. 5–ზე ნაჩვენებია ჰაერის ნაკადში მოთავსებული მბრუნავი ცილინდრის გარშემოდენა. მაგნუსის ეფექტი წარმოიქმნება, მაგალითად, ტენისის ან ფეხბურთის ჩახვეულად მიწოდებული ბურთის ფრენისას.

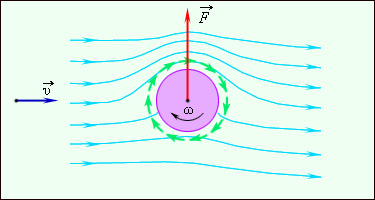
ნახ. 5.

ჰაერის ნაკადში მოთავსებული მბრუნავი ცილინდრის გარშემოდენა.

 

ასე რომ, სველი ხახუნის ძალები მნიშვნელოვან როლს ასრულებს აეროდინამიკის მრავალ მოვლენაში. ისინი იწვევენ თვითმფრინავის ფრთის ან მბრუნავი სხეულის გარშემო ჰაერის ცირკულირებადი ნაკადის შექმნას, გარემოს წინააღმდეგობის ძალების აღძვრას და ა.შ. ბერნულის განტოლება ხახუნის ძალებს არ ითვალისწინებს. მისი დასკვნები დაფუძვნებულია სითხისა და აირების დინებისა მექანიკური ენერგიის მუდმივობაზე. ამიტომაც, ბერნულის განტოვების საშუალებით შეუძლებელია ამომწურავი ახსნა იმ მოვლევებისა, სადაც   ხახუნის ძალები იჩენენ თავს. ასეთ შემთხვევებში შეიძლება მხოლოდ ხარისხობრივი მოსაზრებებით ვიხელმძღვანელოთ - რაც მეტია სიჩქარე აირის ნაკადში, მით ნაკლებია წნევა.

სველი ხახუნის ძალები განსაკუთრებით შესამჩნევად ვლინდება სითხის დინების დროს. ზოგი სითხის სიბლანტე იმდენად დიდია, რომ ბერნულის განტოლების გამოყენებამ შეიძლება ხარისხობრივად ძალინ განსხვავებულ, არასწორ შედეგებამდე მიგვიყვანოს. მადალითად, ბლანტი სითხის ჭურჭკის ხვრელიდან გამოდინებისას, ბერნულის განტოლებით გამოთვლილი მისი სიჩქარე შეიძლება ათეულობითჯერ ნაკლები იყოს ტორიჩელის ფომულით გამოთვლილთან შედარებით. სფერული სხეული იდეალურ სითხეში მოძრაობისას არ უნდა განიცდიდეს არანაირ წინააღმდეგობას. თუ ასეთ სხეული ბლანტ სითხეში მოძრაობს, აღიძვრება წინააღმდეგობის ძალა, რომლის სიდიდე მოძრაობის სიჩქარის \(v\) და სფეროს რადიუსის \(r\) პროპორციულია (სტოქსის კანონი).

\(F_{winaag}\sim v\cdot r.\) 

ამ ფორმულაში პროპორციულობის კოეფიციენტი სითხის თვისებებზეა დამოკიდებული.

ამიტომ, თუ მძიმე ბურთულას ბლანტი სითხით (მაგ. გლიცერინით) სავსე მაღალ ჭურჭელში ჩავაგდებთ, გარკვეული დროის შემდე ბურთულის სიჩქარე მიაღწევს გარკვეული სტაბულურ სიჩქარეს, რომელიც შემდგომი მოძრაობის მანძილზე არ შეიცვლება. ამ სტაბილური სიჩქარით მოძრაობისას ბურთულაზე მოქმედი ძალები (სიმძიმის ძალა \(m\vec{g},\) ამომგდები ძალა \(\vec{F}_{A}\) და გარემოს წინააღმდეგობის ძალა \(\vec{F}_{winaag}\)) კომპენსირებულია (გაწონასწორებილია), და მათი ტოლქმედი ნულის ტოლია.