{loadnavigation}

ბგერით ტალღბს ან უბრალოდ ბგერას უწოდებენ ტალღებს, რომელსაც ადამიანის ყური აღიქვამს. ბგერითი ტალღების სიხშირეთა დიაპაზონი 20 ჰც-დან 20 კჰც-ია.  20ჰც-ზე ნაკლები სიხშირის ტალღებს ინფრაბგერას უწოდებენ. ხოლო  20 კჰც-ზე დიდ სიხშირისას ულტრაბგერას. ბგერის დიაპაზონის ტალღებს შეუძლია გავრცელება არა მარტო აირებში, არამერ სითხეებში (განივი ტალღები) და მყარ სხეულებში (განივი და გრძივი ტალღები).  მაგრამ ტალღები აირებში - ჩვენს სასიცოცხლო გარემოში - იწვევს განსაკუთრებულ ინტერესს. ფიზიკის ნაწილს, რომელიც ბგერით მოვლენებს შეისწავლის, აკუსტიკა ეწოდება.

აირში ბგერის გავრცელებისას ატომები და მოლეკულები ირხევიან ტალღების გავრცელების მიმართულებით . ეს იწვევს ლოკალური სიმკვრივის \(\rho\) და   \(p\)  წნევის ცვლილებას. ბგერით ტალღებს აირში ხშირად სიმკვრივის ტალღებს ან წნევის ტალღებს უწოდებენ.

 

 

\(OX\) ღერძის გასწვრის გავრცელებულ უბრალო ჰარმონიულ ბგერით ტალღებში \(p(x,t)\) წნევის ცვლილება \(x\) კოორდინატასა და \(t\) დროზე დამოკიდებულია კანონით:

 \(p(x,t)=p_{0}\cos (\omega t\pm kx)\).

კოსინუსის არგუმენტში ორი ნიშანი ტალღის გავრცელების ორ მიმართულებაზე მიუთითებს. \(\omega\) სიხშირე, ტალღური რიცხვი \(k\), ტალღის სიგრძე \(\lambda\), ბგერის სიჩქარე \(v\) ისევე როგორც ზამბარის შემთხვევაში გავრცელებულ განივ ტალღებში ტოლია:

\(v=\frac{\lambda}{T}=\frac{\omega}{k};\: k=\frac{2\pi}{\lambda};\:\omega=2\pi f=\frac{2\pi}{T}.\)

ბგერითი ტალღის მნიშვნელოვან მახასიათებელს მისი გავრცელების სიჩქარე წარმოადგენს. ის გარემოს ინერტული და დრეკადი თვისებებით განისაზღვრება.  განივი ტალღის გავრცელების სიჩქარე ნებისმიერ უსასრულოდ ერთგვაროვან გარემოში განისაძღვრება ფორმულით:

\(v=\sqrt{\frac{B}{\rho}},\)

სადაც \(B\) – ყოველმხრივი შეკუმშვის მოდულია, \(\rho\) – გარემოს საშუალო სიმკვრივე. ჯერ კიდევ ნიუტონმი ცდილობდა ჰაერში ბგერის გავრცელების სიჩქარის გამოთვლას. მან დაუშვა, რომ ჰაერის დრეკადობა ტოლია ატმოსფერული წნევის \(p_{atm}\) , მაშინ ბგერის სიჩქარე 300 მ/წმ-ზე ნაკლები გამოდის, მაშინ როცა ბგერის ჭეშმარიტი სიჩქარე ნორმალურ პირობებში   (ე.ი. 0 °С ტემპერატურასა და  1 ატმ წნევაზე)   331,5 მ/წმ-ს ტოლია, ხოლო ბგერის სიჩქარე 20 °С ტემპერატურასა  და  1 ატმ წნევაზე 343 მ/წმ-ს ტოლი ხდება. მხოლოდ ასი წლის შემდეგ ფრანგმა მეცნიერმა ლაპლასმა აჩვენა, რომ ნიუტონის დაშვება ექვივალენტურია დაშვებისა, რომ ტემპერატურა სწრაფად მოდის წონასწორობაში შემკვრივებულ და გაიშვიათებულ უბნებს შორის.  ეს დაშვება ჰაერის ცუდი თბოგამტარობისა და ბგერითი ტალღის რხევების მცირე პერიოდის გამო შეუსრულებადია.  სინამდვილეში აირის შემკვრივებულ და გაიშვიათებულ უბნებს შირის წარმოიქმნება ტემპერატურათა სხვაობა, რომელიც მნიშვნელოვან გვლენას ახდენს აირის დრეკად თვისებებზე. ლაპლასმა დაუშვა, რომ ბგეროთ ტალღაში აირის შეკუმშვა და გაიშვიათება ხდება ადიაბატური კანონით, ე.ი. თბოგამტარობის გავლენის გარეშე. ლაპლასის ფორმულას (1816 წ.) აქვს სახე:

\(v=\sqrt{\frac{\gamma p}{\rho}},\)

სადაც \(p\) – აირის საშუალო წნევაა, \(\rho\) – საშუალო სიმკვრივე, \(\gamma\) – აირის თვისებებზე დამოკიდებული რაღაც მუდმივა.  ორატომიანი აირისათვის \(\gamma=1,4. ლაპლასის ფორმულით ბგერის სიჩქარის გამოთვლა იძლევა სიდიდეს \)v=332\( მ/წმ (ნორმალურ პირობებში).

თერმოდინამიკაში მტკიცდება, რომ  \)\gamma\( კოეფიციენტი თბოტევადობის ტოლია, მუდმივი  წნევის დროს \)C_{p} და მუდმივი მოცულობის დროს  \(C_{V}\) . ლაპლასის ფორმულა შეიძლება სხვა სახით წარმოვადგინოთ, თუ გამოვიყენებთ იდეალური აირის მდგომარეობის  განტოლებას. აქ მოვიყვანთ საბოლოო გამოსახულებას: 

\(v=\sqrt{\frac{\gamma RT}{M}},\)

სადაც \(T\) – აბსოლუტური ტემპერატურაა, \(M\) – ნორმალური მასა, \(R=8,314\) ჯ/მოლი·\(K\) – აირის უნივერსალური მუდმივა. ბგერის სიჩქარე ძლიერაა დამოკიდებული აირის თვისებებზე. რაც უფრო მსუბუქია აირი, მით უფრო მეტია ბგერის სიჩქარე. ასე მაგალითად, ჰაერში (\(M=29\cdot 10^{-3}\) კგ/მოლი) ნორმალურ პირობებში \(v=331,5\) მ/წმ, ჰელიუმში (\(M=4\cdot10^{3}\) კგ/მოლი) υ = 970 მ/წმ, წყალბადში (\(M=2\cdot10^{-3}\) კგ/მოლი) \(v=1270\) მ/წმ.

სითხეებსა და მყარ სხეულებში ბგერითი ტალღების სიჩქარე კიდევ უგრო დიდია. წყალში მაგალითად \(v=1480\) მ/წმ-ს ( 20 °С), ფოლადში \(v=5\, -6\) მ/წმ.

ადამიანის ყური სხვადასხვა ბგერის აღქმისას, მათ პირველ რიგში აფასებს ხმამაღლობის მიხედვით, ბგერითი ტალღის ენერგიის ნაკადის ან ბგერითი ტალღის ინტენსივობაზე დამოკიდებულებით. ბგერითი ტალღის ზემოქმედება ყურის აპკზე ბგერის წნევაზეა დამოკიდებული ე.ი. ტალღის წნევის p₀ რხევის ამპლიტუდაზე.  ადამიანის ყური ბუნების სრულყოფილი ქმნილებაა, რომელსაც ბგერების აღქმა შეუძლია ინტენსივობების უზარმაზარ დიაპაზონში: კოღოს სუსტი წრიპინიდან ვულკანის გრუხუნამდე. სმენადობის ზღვარი შეესაბამება  \(p_{0}\)  მნიშვნელობებს, რომლებიც 10^–10 ატმ რიგისაა, ე.ი.10^-5 პ. ყოველი სუსტი ბგერის გავრცელებისას ჰაერის მოლეკულები ბგერით ტალღაში ირხევიან მხოლოდ და მხოლოდ   10^–7 სმ ამპლიტუდით! ტკივილის ზღვარი შეესაბამება მნიშვნელობებს, რომელთათვისაც   \(p_{0}\)-ს  10^–4 ატმ-ს რიგისაა ანუ 10 პა. ამგვარად, ადამიანის ყურს შეუძლია აღიქვას ტალღები, რომლებშიც ბგერითი წნევა  მილიონჯერ იცვლება. რამდენადაც ბგერის ინტენსივიბა ბგერის წნევის კვადრატის პროპორციულია, ინტენსივობათა დიაპაზონი 10¹² რიგისაა! ადამიანის ყურს, რომელსაც შეუძლია აღიქვას ბგერები ინტენსივობათა ასეთ უზარმაზარ დიაპაზონში, შეიძლება შევადაროთ ხელსაწყოს, რომელიც შეიძლება გამოყენევულ იქნეს ატომის დიამეტრის, ასევე ფეხბურთის მოედნის გასაზომად.

შედარებისათვის მივუთითებთ, რომ ოთახში ჩვეულებრივი საუბრისას ბგერის ინტენსივობა დაახლოებით 10⁶ -ჯერ აჭარბებს სმენადობის ზღვარს, როკ-კონცერტის დროს კი ბგერის ინტენსივობა ტკივილის ზღვართანაა მიახლოებული.

ბგერითი ტალღების კიდევ ერთი მახასიათებელი, რომელიც მათ სმენით აღქმას განსაზღვრავს, არის ბგერის სიმაღლე. ჰარმონიულ ბგერით ტალღაში რხევა ადამისნის ყურის მიერ აღიქმება როგორს მუსიკალური ტონი. მაღალი სიხშირის რხევა აღიქმება როგორც მაღალი ტონის ბგერა, დაბალი სიხშირის რხევა - როგორც დაბალი ტონის ბგერა. მუსიკალური ინსტრუმენტების მიერ გამოცემული ბგერები და ადამიანის მიერ გამოცემული ბგერებიც შეიძლება ძლიერ განსხვავდებოდნენ ტონის სიმაღლითა და სიშორის დიაპაზონით. ასე, მაგალითად, მამაკაცის ხმის ყველაზე დაბალი (ბანი)- დიაპაზონი დაახლოებით 80-დან 400 ჰც-ია, ხოლო ქალის ხმის ყველაზე მაღალი (სოპრანოს) – დიაპაზონი 250-დან 1050 ჰც-მდეა.

ბგერითი რხევების იმ დიაპაზონს, რომელიც რხევის სიხშირის ორჯერ ცვლილებას შეესაბამება ოქტავას უწოდებენ. ვიოლინოს ხმა, მაგალითად, დაახლოებით სამნახევარ ოქტავას ფარავს  (196–2340 ჰც), ხოლო პიანინო - შვიდს აჭარბებს (27,5–4186 ჰც).

როცა საუბრობენ ნებისმიერი სიმიანი ინსტრუმენტის მიერ გამოცემულ ბგერის სიხშირეზე, გულისხმობენ ძირითადი ტონის  \(f_{1}\) - ზე. მაგრამ სიმის რხევებში შეიძლება გვქონდეს ჰარმონიკები  \(f_{n}\) სიხშირით, რომლებსაც შეესაბამება ტოლობა:

\(f_{n}=nf_{1},\: (n=1,2,3...)\).

 ამიტომაც, მჟღერ სიმს შეუძლია ჯერადი სიხშირეების ტალღების მთელი სპექტრის გამოსხივება. ამ ტალღების \(A_{n}\)  ამპლიტუდა დამოკიდებულია სიმის აღგზნების ხერხზე (ხემით, ჩაქუჩით); ისინი განსაზღვრავენ მუსიკალური ბგერის ტემბრს. ანალოგიურადაა საქმე სასულე ინსტრუმენტებშიც. სასულე ინსტრუმენტების მილების აკუსტიკურ რეზონატორებს წარმოადგენენ. ე.ი. აკუსტიკურ რხევით სისტემებს, რომლებსაც გარკვლეული სიხშირის ტალღებისაგან შეუძლია აღიგზნას (დაიწყოს რეზონირება). გარკვეულ პირობებში ჰაერში მილის შიგნით შეიძლება წარმოიქმნას მდგარი ტალღები. ნახ 1 გვიჩვენებს ორღანის მილებში, რომლების ერთი მხრიდან დახურულია და მეორიდან ღია,  მდგარი ტალღის  რამოდენიმე ტიპს (მოდას). სასულე ინსტრუმენტებით გამოცემული ბგერები, შედგებიან ჯერადი სიხშირეების ტალღების მთელი სპექტრისგან.

ნახ. 1.

მდგარი ტალღები ერთი მხრიდან დახურულ და მეორედან ღია საორღანო მილში. ისრები უჩვენებენ ჰაერის ნაწილაკების მოძრაობის მიმართულებას რხევის ერთნახევარი პერიოდის განმავლობაში.

მუსიკალური ინსტრუმენტების აწყობის დროს ხშირად გამოიყენება ხელსაწყო, რომელსაც კამერტონს უწოდებენ. ის შედგება ხის აკუსტიკური რეზონატორისა და მასზე დამაგრებული მეტალის ჩანგლისაგან, რომლებიც რაზონანსურადაა აწყობილი. ჩაქუჩის დარტყმისას ჩანგალზე მთელი სისტემა აღიგზნება და გამოსცემს სუფთა მუსიკალურ ტონს.

მუსიკალურ რეზონატორს წაროადგენს მომღერლის ყელიც. ნახ 3-ზე წარმოდგენილია ბგერითი ტალღების სპექტრი, რომელსაც გამოსცემს კამერტონი, პიანინოს სიმი და ქალის დაბალი ხმა (ალტი), რომლების ერთი და იგივე ნოტზე ჟღერენ.

 

ნახ. 2.

კამერტონის (1), პიანინოს (2) და ქალის დაბალი ხმის (ალტი) (3) მიერ გამოცემული ბგერითი ტალღების სპექტრში ჰარმონიკების ფარდობითი ინტენსივიბები, რომლებიც ჟღერს კონტროქტავის „ლა“ ნოტში. ორდინატთა ღერძზე გადაზომილია ფარდობითი ინტენსივობები.

ნახ. 2-ზე მოცემული სიხშირული სპექტრის ბგერითი ტალღებს აქვთ ერთი და იგივე სიმაღლე და განსხვავებული ტემბრი.

ახლა განვიხილოს მოვლენა, რომელიც ორი ახლო, მაგრამ მაინც განსხვავებული სიხშირეების ბგერითი ტალღის ზედდებისას წარმოიქმნება. ამ მოვლენას ფეთქვა(პულსაცია) ეწოდება. მას ადგილი აქვს, მაგალითად, ზუსტად ერთნაირ სიხშირეზე აწყობილი  ორი კამერტონის ან გიტარის ორი სიმის ერთროული ჟღერისას. ფეთქვა ყურის მიერ აღიქმება როგორც ჰარმონიული ტონი, რომლის ხმამაღლობა დროში პერიოდულად იცვლება. ვთქვათ ყურზე მომქმედი ბგერითი წნევები  \(p_{1}\) დაბ\(p_{2}\) იცვლებიან შემდეგი კანონით:

\(p_{1}=A_{0}\cos\omega_{1}t\)  და \(p_{2}=A_{0}\cos\omega_{2}t\).

სიმარტივისათვის ჩავთვალოთ, რომ ბგერითი წნევების რხევების ამპლიტუდები ერთნაირია და უდრის \(p_{0}=A_{0}\).

სუპერპოზიციის პრინციპის თანახმად ორივე ტალღით გამოწვეული სრული წნევა დროის ყოველ მომენტში ტოლია დროის იგივე მომენტში თითოეული ტალღის მიერ გამოწვეული ბგერითი ტალღების წნევების ჯამისა.

ორივე ტალღის ჯამური მოქმედება, ტრიგონომეტრული გარდაქმნების შემდეგ შეიძლება ასე წარმოვადგინოთ

\(p=p_{1}+p_{2}=2A_{0}\cos\left (\frac{\omega_{1}-\omega_{2}}{2}t \right )\cos\left (\frac{\omega_{1}+\omega_{2}}{2}t \right )=2A_{0}\cos\left ( \frac{1}{2}\Delta\omega t \right )\cos(\bar{\omega}t),\)

სადაც \(\Delta\omega=\omega_{1}-\omega_{2},\) და \(\bar{\omega}=\frac{\omega_{1}+\omega_{2}}{2}.\)

ნახ. 3 (1)-ზე მოცემულია \(p_{1}\) და \(p_{2}\) წნევების დამოკიდებულება \(t\) დროზე. \(t=0\) მომენტში ორივე რხევა ფაზაში იმყოფება და მათი  ამპლიტუდები იკრიბება. რადგანაც რხევის სიხშირეები ცოტათი განსხვავდებიან ერთმანეთისაგან, გარკვეული \(t_{1}\)დროის შემდეგ რხევები საწინააღდეგო ფაზებში აღმოჩნდებიან. ამ დროს ჯამური ამპლიტუდა ნულის ტოლი ხდება (რხევები ერთმანეთს „აქრობენ“).   დროის \(t_{2}=2t_{1}\)  მომენტში რხევები ისევ ფაზაში აღმოჩნდებიან და ა.შ. (ნახ. 3 (2)).

დროის მინიმალურ ინტერვალს რხევის ორ მაქსიმალურ (ან მინიმალურ) ამპლიტუდის მომენტს შორის ფეთქვის პერიოდი ეწოდება \(T_{F}\)_.  ჯამური რხევის \(A\) ნელა ცვლადი ამპლიტუდა  ტოლია:

\(A=2A_{0}\left | \cos\frac{1}{2}\Delta\omega t \right |.\)

ამპლიტუდის ცვლილების \(T_{F}\)  პერიოდი ტოლია \(\frac{2\pi}{\Delta\omega}\). ეს სხვა ხერხითაც შეიძლება ვაჩვენოთ, დავუშვათ, რომ წნევის რხევის პერიოდები ბგერით ტალღებში   \(T_{1}\) და \(T_{2}\) ისეთია, რომ \(T_{1}<T_{2}\) (ე.ი. \(\omega_{1}>\omega_{2}\)). ფეთქვის პერიოდში\(T_{F}\) ადგილი აქვს პირველი ტალღის რხევის რაღაც \(n\) რაოდენობის სრულ ციკლს და \((n-1)\) ცალი მეორე ტალღის რხევების ციკლს: 

\(T_{F}=nT_{1}=(n-1)T_{2}\).

აქედან გამოდის:

\(T_{F}=\frac{T_{1}T_{2}}{T_{2}-T_{1}}=\frac{2\pi}{\omega_{1}-\omega_{2}}=\frac{2\pi}{\Delta\omega}\) ან \(f_{F}=\frac{1}{T_{F}}=\frac{1}{T_{1}}-\frac{1}{T_{2}}=f_{1}-f_{2}=\Delta f.\)

ფეთქვის სიშირე \(f_{F}\) ტოლია ორი ბგერითიტალღის სიხშირეთა სხვაობისა \(\Delta f\), რომელსაც ყური ერთდროულად აღიქვამს.

ადამიანი ბგერით ფეთქვას აღიქვამს 5-10 ჰც სიხშირეებამდე. ფეთქვის მოსმენა მუსიკალური ინსტრუმენტების აწყობის ტექნიკის ნმიშვნელოვანი ელემენტია.

ნახ.2.7.3.

პულსაცია (ფეთქვა), რომელიც ორი მახლობელი სიხშირის ბგერითი ტალღის ზედდებით მიიღება.

{loadnavigation}

თუ მყარ, თხევად ან  აიროვანი გარემოს რაღაც წერტილში აღიძვრება ნაწილაკების რხევა, მაშინ გარემოს ატომებისა და მოლეკულების  ურთიერთქმედების შედეგად რხევებეს გადაცემა დაიწყება ერთი წერტილიდან მეორეზე სასრული სიჩქარით. რხევების გავრცელების პროცესს ტალღები ეწოდება.

არსებობს სხვადასხვა სახის მექანიკური ტალღები. 

თუ გარემოს ნაწილაკები განიცდიან ტალღის გავრცელების მართობული მიმართულებით გადაადგილებას, მაშინ ტალღას განივს უწოდებენ. ამგვარი ტალღების მაგალითად გამოდგება ტალღები, რომლებიც გაჭიმულ რეზინაზე ან სიმზე მოძრაობს (გარბის) (ნახ. 1).

თუ გარემოს ნაწილაკების გადანაცვლება ხდება ტალღის გავრცელების მიმართულებით, მაშინ ტალღას გრძივს უწოდებენ. ტალღები დრეკად ღეროში ან ბგერითი ტალღები აირში ასეთი ტალღების მაგალითს წარმოადგენენ.

 

 

როგორც განივ, ასევე გრძივ ტალღებში ნივთიერების გადატანა არ ხდება. გავრცელების პროცესში გარემოს ნაწილაკები მხოლოდ რხევას ასრულებენ წონასწორობის მდებარეობის მახლობლად. მიუხედავად ამისა, ტალღებს რხევის ენერგია გადააქვს ერთი წერტილიდან მეორეში.

ნახ. 1.

გაჭიმულ რეზინის ზონარზე განივი ტალღური იმპულსის გავრცელება.

 

 

ნახ. 2.

დრეკად ღეროში გრძივი ტალღური იმპულსის გავრცელება.

 

მექანიკური ტალღების დამახასიათებელ თავისებურებას წარმოადგენს, ის რომ ისინი მატერიალურ გარენოში ვრცელდებიან (მყარ, სითხესა და აირებში). არსებობენ ტალღები, რომლებსაც სიცარიელეში გავრცელება შეუძლია (მაგალითად სინათლის ტალღები). მექანიკური ტალღებისათვის აუცილებელია გარემო, რომელსაც შეუძლია კინეტიკური და პოტენციური ენერგიის მარაგის შექმნა. ე.ი., გარემოს უნდა ჰქონდეს ინერტულობა და დრეკადი თვისებები.  მაგალითად, მყარი სხეულის ნებისმიერ მცირე ელემენტს აქვს მასა და დრეკადობა. უმარტივეს მოდელში მყარი სხეული შეიძლება წარმოვიდგინოთ როგორც პატარა ბურთულებისა და ზამბარების ერთობლიობა (ნახ. 3).

ნახ. 3.

მყარი სხეულის უმარტივესი ერთგანზომილებიანი მოდელი

 

ამ მოდელში ინერტული და დრეკადი თვისებებიბი განცალკევებულია. ბურთულებს \(m\)  მასა აქვთ, ზამბარებს – \(k\)  დრეკადობა. ამ უბრალო მოდელის საშუალებით შეიძლება აღიწეროს განივი და გრძივი ტალღების გავრცელება მყარ სხეულში. განივ ტალღებში ბურთულები განიცდიამ ჯაჭვის გასწვრივ გადაადგილებას, ზამბარები კი იჭიმბიან ან იკუმშებიან. ასეთ დეფორმაციას გაჭიმვის ან შეკუმშვის დეფორმავია ეწოდება. სითხეებსა და გაზებში ასეთ დეფორმაციას თან ახლავს შემკვრივება ან გაიშვიათება.

განივ მექანიკურ ტალღებს გავრცელაბა შეუძლიათ ნებისმიერ, მყარ, თხევად და აირად გარემოში. თუ მყარი სხეულის ერთგანზომილებიან მოდელში ერთ ან რამდენიმე ბურთულას წავანაცვლებთ ჯაჭვის მართობული მიმართულებით, ნაშინ წაროიშვემა წანაცვლების დეფორმაცია, ასეთი წანაცვლებისას დეფორმირებული ზამბარა ცდილობს წანაცვლებული ნაწილები დააბრუნოს წონასწორობაში. ამასთან, უახლოეს წანაცვლებულ ნაწილებზე მოქმედებენ დრეკადობის ძალები, რომლებიც შეეცდებიან მათ გადახრას წონასწორობიდან. ამის შედეგად ჯაჭვის გასწვრივ გაირბენს განივი ტალღა. სითხეებსა და გაზებში წანაცვლების დეფორმაცია არ აღიძვრება.

თუ სითხის ან გაზის ფენას წავანაცვლებთ სხვა ფენების მიმართ, ფენებს შირის საზღვარზე არავითარი შეხების ძალები არ აღიძვრება. ძალები, რომლებიც მოქმედებენ სითხისა და მყარი სხეულის საზღვარზე, და ასევე სითხის ფენებს შორის ყოველთვის ამ საზღვრის მიმართ მართობულადაა მიმართული. ეს წნევის ძალაა. ასევეე გაზებშიც. აქედან გამომდინარე, განივი ტალღები ვერ აღიძვრება თხევად და აირად გარემოში.

დიდი პრაქტიკული ინტერესი დაკავშირებულია უბრალო ჰარმონიული ანუ სინუსოიდური ტალღების გავრცელაებასთან. ისინი ხასიათდებიან ნაწილაკის რხევის \(A\)  ამპლიტუდით, სიხშირით -\(f\)  და ტალღის სიგრძით -\(\lambda\) . სინუსოიდური ტალღები ერთგავაროვან გარემოში ვრცელდებიან გარკვეული \(v\)  სიჩქარით. გარემოს ნაწილაკების წონასწორობის მდებარეობიდან წანაცვლება \(y(x,t)\)  დამოკიდებულია  \(OX\)  ღერძზე \(x\)  კოორდინატზე, რომლის გასწვრივაც ვრცელდება ტალღა და \(t\)   დროზე, კანონით:

\(y(x,t)=A\cos \omega\left (t-\frac{x}{v} \right )=A\cos(\omega t-kx),\)

სადაც \(k=\frac{\omega}{v}\)  – ე.წ. ტალღური რიცხვია,  \(\omega=2\pi f\)  – წრიული სიხშირე. ნახ. 4–ზე მოცემულია განივი ტალღის ორი დროითი მომენტის  \(t\) stststt" style="margin: 0px; padding: 0px; width: 6px; height: 12px;" /> და \(t+\Delta t\)  "მომენტალური ფოტოგრაფია“.   \(\Delta t\)  დროის განმავლობაში ტალღამ \(OX\)  ღერძის გასწვრივ გადაინაცვლა \(\Delta x\)  მანძილძე. თუ ტალღის ყველა წერტილი ერთიდაიგივე სიჩქარით გადაადგილდება მას მორბენალ ტალღას უწოდებენ (მდგარი ტალღისგან განსხვავებით).

ნახ. 4. მორბენალი სინუსოიდური ტალღის „მომენტალური ფოტოგრაფია“  დროის \(t\)  და \(t+\Delta t\)    მომენტებში.

ტალღის სიგრძე  \(\lambda\)  ეწოდება \(OX\)   ღერძზე ორ, ერთნაერ ფაზაში მერხევ, მეზობელ წერტილს შორის მანძილს .   λ ტალღის სიგრძის ტოლ მანძილს ტალღა გაირბენს \(T\)  ის განმავლობაში, ე.ი. \(\lambda=vT\) , სადაც \(v\)  –ტალღის გავრცელების სიჩქარეა. გრაფიკზე , ნებისმიერი შერჩეული წერტილისათვის ტალღური პროცესისთვის  \(t\)  დროის ცვლილებისას \(x\)  კოორდინატაც იცვლება ხოლო გამოსახულება \(\omega t-kx\)  უცვლელი რჩება.  \(\Delta t\)  დროის შემდეგ \(A\)  წერტოლი გადაადგილდება \(OX\)  ღერძის გასწვრივ რაღაც \(\Delta x=v\Delta t\)  მანძილზე. მაშასადამე:  

\(\omega t-kx=\omega(t-\Delta t)-k(x+\Delta x)=const\)   ან  \(\omega \Delta t=k\Delta x\) .

აქედან გამოდის:

\(v=\frac{\Delta x}{\Delta t}=\frac{\omega}{k}\)  ან  \(k=\frac{2\pi}{\lambda}=\frac{\omega}{v}.\)

ამრიგად, მორბენალ სინუსოიდურ ტალღას ორმაგი პერიოდი აქვს - დროითი და სივრცული. დროითი პერიოდი გარემოს \(T\)  ნაწილაკების რხევის პერიოდის ტოლია, სივრცული პერიოდი კი ტალღის \(\lambda\)  სიგრძის. ტალღური რიცხვი \(k=\frac{2\pi}{\lambda}\)   წრიული სიხშირის \(\omega =\frac{2\pi}{T}\)   სივრცულ ანალოგს წარმოადგენს.

ყურადღება მივაქციოთ იმას, რომ განტოლება

\(y(x,t)=A\cos(\omega t+kx)\)

აღწერს იმ სინუსოიდურ ტალღებს, რომლებიც \(OX\)  ღერძის საწინააღმდეგო მიმართულებით ვრცელდება \(v=-\frac{\omega}{k}\)  სიჩქარით.

მორბენალ სინუსოიდურ ტალღაში გარემოს ყოველი ნაწილაკი ასრულებს ჰარმონიულ რხევას რაღაც \(\omega\)  სიჩქარით. ამიტომ , ჩვეულებრივი რხევითი პროცესის მსგავსად, გარემოს რაღაც მოცულობის საშუალო პოტენციური ენერგიის მარაგი ტოლია იგივე მოცულობის საშუალო კინეტიკური ენერგიისა და პროპორციულია რხევის ამპლიტუდის კვადრატისა.

აქედან გამომდინარეობს, რომ მორბენალი ტალღის გავრცელაებისას წარმოიქმნება ენერგიის მარაგი, რომელიც პროპორციულია ტალღის სიჩქარისა და ამპლიტუდის კვადრატისა.

მორბენალი ტალღების  გარემოში გავრცელების  სიჩქარე ტალღის ტიპსა და გარემოს ინერტულ და დრეკად თვისებებზეა დამოკიდებული.

გრძივი ტალღების სიჩქარე გაჭიმულ სიმში ან რეზინის ზონარში დამოკიდებულია სიგრძის ერთულის \(\mu\)   მასასა და \(T\) დაჭიმულიბის ძალაზე:

\(v=\sqrt{\frac{T}{\mu}}.\)

უსასრულო გარემოში განივი ტალღის გავრცელაების სიჩქარე განისაზღვრება გარემოს სიმკვრივითა და \(B\)  ყოველმხრივი შეკუმშვის მოდულით, რომელიც წნევის ცვლილებასა და ფარდობით მოცულობას შორის პროპორციულობის კოეფიციენტის (საწინააღმდეგო ნიშნით აღებული) ტოლია:

\(\Delta p=-B\frac{\Delta V}{V}.\)

უსასრულო გარემოში  განივი ტალღის გავრცელაების სიჩქარის გამოსახულებას აქვს სახე:

\(v=\sqrt{\frac{B}{\rho}}.\)

მაგალითად, 20 °С ტემპერატურაზე განივი ტალღის გავრცელაების სიჩქარე წყალში υ ≈ 1480 მ/წმ, სხვადასხვა ხარისხის ფოლადში კი   υ ≈ 5–6 კმ/წმ.

განივი ტალღის დრეკად ძელში გავრცელებისას ყოველმხრივი შეკუმშვის მოდულის ნაცვლად შედის იუნგის მოდული \(E\)  ( იხ. პარაგრაფი 1,12):

\(v=\sqrt{\frac{E}{\rho}}.\)

ფოლადისათვის განსხვავება \(E\)  და \(B\) -ს შორის დიდი არ არის. სხვა მასალებისთვის კი შეიძლება 20–30 % და მეტიც იყოს.

თუ მექანიკური ტალღა, გარემოში გავრცელებისას ხვდება რაიმე წიმააღმდეგობას, მას შეუძლია მკვეთრად შცვალის თავისი ყოფაქცევა. მაგალითად, ორი გამსხვავებული მექანიკური თვისებების მქონე გარემოს საზღვარზე ტალღა ნაწილობრივ აირეკლება და ნაწილობრი შეაღწევს მეორე გარემოში. რეზინის ზონარზე მორბენალი ტალღა აირეკლება უძრავად დამაგრებული ბოლოდან; ამ დროს წარმოიქმვბა საწიმააღმდეგოდ მორბენალი ტალღა. ორივე ბოლოთი დამაგრებულ სიმში აღიძვრება რთული რხევები, რომლებიც შეიძლება ორი ურთიერთსაწიააღმდეგოდ გავრცელებული ტალღის ზედდებად (სუპერპოზიციად) განვიხილიდ, რომლებიც არეკვლას და არეკლილის ისევ არეკვლას განიცდის. ორივე ბოლოთი დამაგრებულ სიმში აღძრული რხევები წარმოქმნიან ყველა სიმიანი ინსტრუმენტის ჟღერადობას. ძალიან მსგავს მოვლენას აქვს ადგილო სასულე ინსტრუმენტებში, მათ შორის ორღანშიც.

თუ სიმში შემხვედრი მიმართულებით მორბენალი ტალღები სინუსოიდური ფორმისაა, მაშინ გარკვეულ პირობებში შეიძლება წარმოიქმნას მდგარი ტალღები.

ვთქვათ  \(l\)   სიგრძის სიმი ისეა დამაგრებული, რომ ერთერთი მისი ბოლო  \(x=0\)  წერტილშია, მეორე კი –   \(x_{1}=L\)  წერტილში (ნახ. .5). სიმში შექმნილია \(T\)  დაჭიმულობა.

 

ნახ.5.

სიმში მდგარი ტალღის წარმოქმნა.

მაშინ სიმში ერთდროულად ვრცელდება ერთიდაიგივე სიხშირის ურთიერთსაწინააღმდეგო ტალღა:

• \(y_{1}(x,t)=A\cos(\omega t+kx)\)  – მარჯვნიდან მარცხნივ მორბენალი ტალღა;

• \(y_{2}(x,t)=-A\cos(\omega t-kx)\)  – მარცხნიდან მარჯვნივ მორბენალი ტალღა.

\(x=0\)  წერტილში დაცემული ტალღა  \(y_{1}\)  არეკვლის შედეგად წარმოქმნის  \(y_{2}\)  ტალღას. უძრავად დამაგრებულ ბოლოზე არეკლილი ტალღა საწინააღმდეგო ფაზაშია დაცემულის მიმართ. სუპერპოზიციის პრინციპის თანახმად, რა ექსპერიმენტულ ფაქტს წარლოადგენს, შემხვედრი ტალღებით გამოწვეული  რხევა სიმის ყიველ წერტილში იკრიბება.  

ე.ი. ჯამური რხევა ყოველ წერტილში ტოლია  \(y_{1}\)  და \(y_{2}\)  ცალცალკე გამოწვეული რხევების ჯამისა.

 \(y=y_{1}(x,t)+y_{2}(x,t)=(-2A\sin \omega t)\sin kx\) .

სწორედ ესაა მდგარი ტალღა. მდგარ ტალღაში არსებობს უძრავი წერტილები რომლებსაც კვანძებს უწოდებენ. კვანძებს შორის არის წერტილები რომლებიც მაქსიმალური ამპლიტუდით ირხევიან.

ორივე უძრავი ბოლო კვანძს უნდა წარმოადგენდეს. ზემოთ მოყვანილი ფორმულა ამ პირობას მარცხენა (\(x=0\) ) ბოლო აკმაყოფილებს. ამ პირობის მარჯვენა (\(x=L\) ) ბოლოზეც შესრულებისთვის აუცილებელია  \(kL=n\pi\) , სადაც \(n\)  – ნებისმიერი მთელი რიცხვია. ეს ნიშნავს, რომ სიმზე  მდგარი ტალღა ყოველთვის არ აღიძვრება. იგი აღიძვრება მხოლოდ მაშინ თუ სიმის \(L\)  სიგრძე ტალღის სიგრძის ჯერეადია:

\(l=n\frac{\lambda_{n}}{2}\)  ან \(\lambda_{n}=\frac{2l}{n}\: (n=1,2,3,...)\)

\(\lambda_{n}\)  ტალღის სიგრძეთა მნიშვნელობები შეესაბამება \(f_{n}\)  სიხშირეების შესაძლო მნიშვნელეობებს: 

\(f_{n}=\frac{v}{\lambda_{n}}=n\frac{v}{2l}=nf_{1},\)

სადაც \(v=\sqrt{\frac{T}{\mu}}\)  – განივი ტალღების სიმის გასწვრივ გავრცელების სიჩქარეა. ყოველი \(f_{n}\)  სიხშირეს და მასთან დაკავშირებული  რხევის ტიპს  ნორმალურ მოდას უწოდებენ. უმცირეს \(f_{1}\)   სიხშირეს ძირითად სიხშირეს უწოდებენ, ყველა დანარჩენს (f₂, f₃, …) ჰარმონიკებს უწოდებენ. ნახ. 5 -ზე \(n=2\)  ნორმალური მოდაა გამოსახული.

მდგარ ტალღაში არაა ენერგიის ნაკადი. სიმის მონაკვეთებში მოქცეული ენერგიის ტრანსპორტირება (გადატანა) არ ხდება სიმის სხვა ნაწილებში. ყოველ ასეთ მონაკვეთში ხდება  პერიოდული (ორჯერ \(T\)  პერიოდის განმავლობაში) გარდაქმნა კინეტიკური ენერგიის  პოტენციურ ენერგიად და პირიქით, როგორც ჩვეულებრივ რხევით სისტემაში. მაგრამ ტვირთიანი ზამბარისა და მათემატიკური ქანქარასგან განსხვავებით, რომლებსაც აქვთ ერთადერთი საკუთარი \(f_{0}=\frac{\omega_{0}}{2\pi},\)  სიხშირე, სიმს საკუთარი სიხშირეების  \(f_{n}\)   უსასრულო რაორენობა აქვს. ნახ.6-ზე ორმხრივად დამაგრებული სიმში მდგარი ტალღის რამოდენიმე ტიპია მოცემული.

 

ნახ. 6.

ორმხრივად დამაგრებული სიმში მდგარი ტალღის პირველი ხუთი ნორმალური მოდა.

სუპერპოზიციის პრინციპის თანახმად სხვადასხვა ტიპის მდგარი ტალღები (ე.ი \(n\) -ის სხვადასხვა მნიშვნელობით) შეიძლება ერთდროულად არსებობდეს მერხევ სიმში.

{loadnavigation}

რხევებს, რომლებიც გარე, პერიოდული ძალების მოქმედებით მიმდინარეობს, იძულებითი ეწოდება.

ამ შემთხვევაში გარეშე ძალა ასრულებს დადებით მუშაობას და უზრუნველყოფს მერხევ სისტემაში ენერგიის მოდინებას. მიუხედავად ხახუნის ძალების მოქმედებისა, ის რხევას მილევის საშუალებას არ აძლევს.

პერიოდული გარე ძალა შეიძლება სხვადასხვა კანონით იცვლებოდეს დროში. განსაკუთრებულ ინტერესს იწვევს შემთხვევა, როცა გარეშე ძალა, რომელიც \(\omega\) სიხშირით, ჰარმონიული კანონით იცვლება, მოქმედებს მერხევ სისტემაზე, რომელსაც   შეუძლია საკუთარი რხევის შესრულება რაღაც \(\omega_{0}\) სიხშირით.

თუ თავისუფალი რხევა ω₀ სიხშირით ხდება, რომელიც განისაზღვრება სისტემის პარამეტრებიდან. მაშინ იძულებითი რხევა ყოველთვის გარეშე ძალის \(\omega\) სიხშირეზე მიმდინარეობს.

 

მერხევ სისტემაზე გარე ძალის მოქმედების დაწყებიდან საჭიროა რაღაც \(\Delta t\) დროის გასვლა იძულებითი რხევის დადგომამდე. ეს დრო რიგის მიხედვით ტოლია მერხევი სისტემის თავისუფალი რხევის მილევის \(\tau\) რდოისა.

საწყის მომენტში მერხევ სისტემაში აღიძვრება ორივე პროცესი – ω სიხშირის იძულებითი რხევა და თავაისუფალი რხევა საკუთარი \(\omega_{0}\) სიხშირით. მაგრამ თავისუფალი რხევა მიილევა გარდუვალი ხახუნის ძალების არსებობის გამო. ამიტომ რაღაც დროის შემდეგ მერხევ სისტემაში რჩება მხოლოდ მაიძულებელი ძალის \(\omega\) სიხშირის სტაციონალური რხევა.

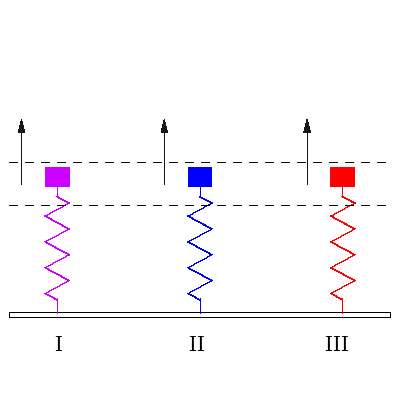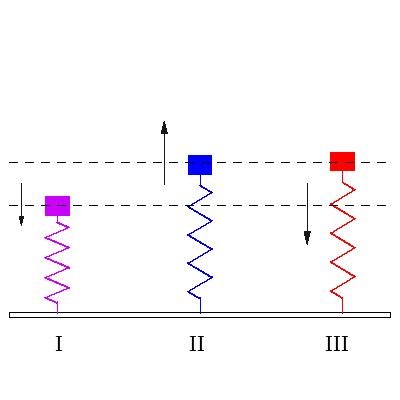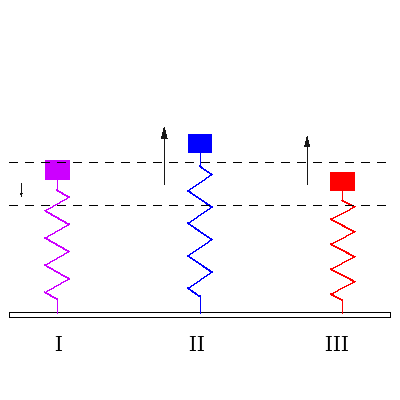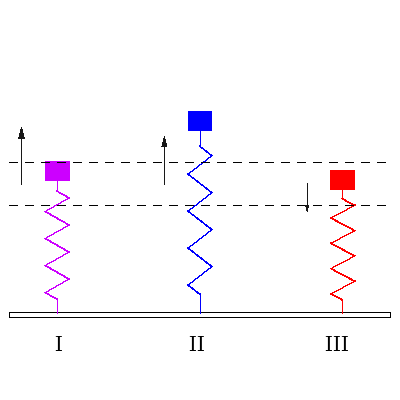I იძულებითი რხევის დასაწყისი, როცა გვაქვს ორივე გარეშე ძალის სიხშირე და ქანქარას სიხშირე ერთად. II. ჩამოყალიბებული რეზონანსი, როცა გარე ძალის სიხშირე ემთხვევა ქანქარას საკუთარ სიხშირეს. III. ჩამოყალიბებული იძულებითი რხევა, როცა ზამბარის საკუთარი სიხშირით რხევა მიილია და ის ირხევა გარეშე ძალის სიხშირით.

მაგალითისთვის განვიხილოთ ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევა (ნახ. 2.5.1). გარეშე ძალა \(\vec{F}_{gare}\) ზამბარის თავისუფალ ბოლოზეა მოდებული.  ის ზამბარის ბოლოს აიძულებს გადაადგილდეს კანონით:

\(y=y_{m}\cos \omega t\).

სადაც  y_m – რხევის ამპლიტუდაა, ω – წრიული სიხშირე.

 

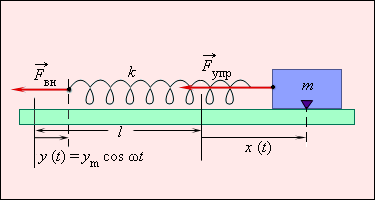
ნახ. 1.

ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევა. ზამბარის თავისუფალი ბოლო გადაადგილდება კანონით \(y=y_{m}\cos \omega t\). \(l\) – დეფორმირებული ზამბარის სიგრძე, \(k\) – ზამბარის სიხისტე.

 

თუ ზამბარის დეფორმაციის შედეგად მისი მარცხენა ბოლო საწყისი მდებარეობიდან  \(y\) მანძილზეა წანაცვლებული, ხოლო მარჯვენა – \(x\)–ზე,  მაშინ ზამბარის წაგრძელება Δl ტოლია: 

\(\Delta l=x-y=x-y_{m}\cos\omega t\).

\(M\) მასის სხეულისთვის ნიუტონის მეორე კანონი მიიღებს სახეს:

\(ma=-k(x-y)=-kx+ky_{m}\cos \omega t\).

ამ განტოლებაში სხეულზე მომქმედი ძალა ორი შესაკრების სახითაა წარმოდგენილი. მარჯვენა მხარეს პირველი შესაკრები დრეკადი ძალაა, რომელიც სხეულის წონასწორობაში (\(x=0\)) დაბრუნებას ცდილობს. მეორე შესაკრები – სხეულზე გარე პერიოდული ზემოქმედებაა. სწორედ ამ შესაკრებს უწოდებენ მაიძულებელ ძალას.

ამ განტოლებას შეიძლება მივცეთ მკაცრი მათემატიკური სახე, თუ გავიხსენებთ კავშირს სხეულის აჩქარებასა და კოორდინატს შორის: \(a=x''\). მაშინ იძულებითი რხევის განტოლება ჩაიწერება შემდეგი სახით:

\(x''+\omega_{0}^{2}x=A\cos\omega t,\)   (**)

სადაც \(\omega_{0}=\sqrt{\frac{k}{m}}\) – მაიძულებელი ძალის ციკლური სიხშირე. ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევის შემთხვევაში (ნახ. 1) \(A\) სიდიდე განისაზღვრება გამოსახულებით:

\(A=\frac{k}{m}y_{m}=\omega_{0}^{2}y_{m}.\)

განტოლება  (**) ხახუნის ძალებს არ ითვალისწინებს. თავისუფალი რხევის განტოლებისგან (*) განსხვავებით იძულებითი რხევის განტოლება (**) შეიცავს ორ სიხშირეს  – თავისუფალი რხევის სიხშირეს \(\omega_{0}\) და მაიძულებელი რხევის სიხშირეს \(\omega\).

საბოლოოდ ზამბარაზე დამყარებული ტვირთის იძულებითი რხევა გარედან ზემომქმედების სიხშირით მიმდინარეობს შემდეგი კანონით

  \(x(t)=x_{m}\cos(\omega t+\theta )\).

იძულებითი რხევის ამპლიტუდა \(x_{m}\) и და ფაზა \(\theta\) დამოკიდებილია \(\omega_{0}\)–ს და \(\omega\)–ს თანაფარდობაზე და გარე ძალის ამპლიტუდაზე <m>m>y_m .

ძალიან დაბალი სიხშირეებისთვის, როცა \(\omega<<\omega_{0}\),  ზამბარის მარჯვენა ბოლოსთან მიმაგრებული \(m\) მასის სხეულის მოძრაობა მარცხენა ბოლოს მოძრაობას იმეორებს. ამასთან \(x(t)=y(t)\), და ზამბარა პრაქტიკულად დეფორმირებული რჩება. ზამბარის მარცხენა ბოლოზე მოდებული გარეშე ძალა \(\vec{F}_{gare}\) მუშაობას არ ასრულებს, რადგან მისი ძალის მოდული როცა \(\omega<<\omega_{0}\) ნულისაკენ მიისწაფის.

თუ გარე ძალის სიხშირე \(\omega\) თავისუფალ სიხშირეს \(\omega_{0}\)–ს უახლოვდება ხდება იძულებითი რხევის ამპლიტუდის მკვეთრი ზრდა. ამ მოვლევას რეზონანსს უწოდებენ.  იძულებითი რხევის ამპლიტუდის \(x_{m}\) მაიძულებელი ძალის სიხშირეზე \(\omega\)დამოკიდებულებას რეზონანსულ მახასიათებელს ან რეზონანსილ მრუდს უწოდებენ (ნახ. 2).

რეზონანსის დროს ტვირთის რხევის ამპლიტუდა \(x_{m}\) ბევრად აღემატება ზამბარის თავისუფალი ბოლოს გარე ზემოქმედებით გამოწვეული რხევის ამპლიტიდა \(y_{m}\)–ს. ხახუნია არ არსებობისას იძულებითი რხევის ამპლიტუდა რეზონანსის შემთხვევაში შეუზღუდავად უნდა იზრდებოდეს. რეალურ პირობებში დამყარებული იძულებითი რხევის ამპლიტუდა განისაზრვრება პირობით: გარე ძალის მუშაობა რხევის პერიოდის განმავლობაში ტოლი უნდა იყოს იგივე დროში ხახუნით გამოწვეული მექანიკური ენერგიის კარგვისა. რეზონანსის დროს,რაც ნაკლებია ხახუნი (ე.ი. რაც მეტია მერხევი სისტემის ვარგისიანობა \(Q\)), მით მეტია იძულებითი რხევის ამპლიტუდა.

არც თუ მაღალი ვარგისიანობის მქონე (< 10) მერხევი სისტემის რეზონანსული ამპლიტუდის მცირე სიხშირეებისკენ ჩანაცვლება ხდება. ეს კარგად ჩანს ნახ. 2–ზე.

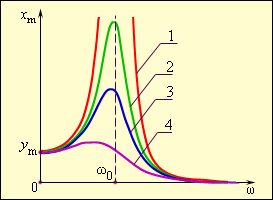
ნახ. 2.

რეზონანსული მრუდები მილევის სხვადასხვა  დონისთვის: 1 - რხევითი სისტემა ხახუნის გარეშე: რეზონანსის დროს იძულებითი რხევის ამპლიტუდა \(x_{m}\)  იზრდება: 2,3,4, - სხვადასხვა ვარგისიანობის მქონე რხევითი სისტემის რეალური რეზონანსული მრუდები: \(Q_{2}>Q_{3}>Q_{4}\). დაბალ სიხშირეებზე (\(\omega << \omega_{0}\)) \(x_{m}\approx y_{m}\). მაღალ სიხშირეებზე (\(\omega >>\omega_{0}\)) \(x_{m}\rightarrow 0.\)

 

იძულებითი რხევები მიულევადი რხევებია. ხახუნზე ენერგიის გარდაუვალი კარგვა კომპენსირდება  გარე პერიოდული ძალის წყაროს მხრიდან. არსებობენ სისტემები, რომლებშიც რხევის მიულევადობა მიიღწევა არა გარე პერიოდული ზემოქმედებით, არამედ ასეთი სისტემების შესაძლებლობით თვითონ არეგულიროს ენერგიის მოწოდება მუდმივი წყაროდან. ასეთ სისტემებს თვითმერხევს და ასეთ სისტემებში მიულევადი რხევის პროცესს ავტორხევითს უწოდებენ. ავტომერხევ სისტემაში შეიძლება გამოვყოთ სამი მახასიათებელი ელემენტი –მერხევი სისიტემა, ენერგიის წყარო და უკუკავშირის მოწყობილობა სისტამასა და ენერგიის წყაროს შორის. მერხევ სისტემად შეიძლება გამოყენებულ იქნეს ნებისმიერი მექანიკური სისტემა, რომელსაც შეუძლია საკუთარი მილევადი რხევის შესრულება (მაგ. კედლის საათის ქანქარა).

ენერგიის წყაროდ შეიძლენა გამოდგეს ზამბარის დეფორმაციის ენერგია ან მიზიდულობის ველში ტვირთის პოტენციური ენერგია. უკუკავშირის მოწყობილობა წარმოადგენს რაღაც მექანიზმს, რომლითაც თვითმერხევი სისტემა არეგულირებს წყაროდან ენერგიის მიწოდებას. ნახ. 3–ზე თვითმერხევი სისტემის სხვდასხვა ელემენტების ურთიერთქმედების სქემაა გამოსახული.

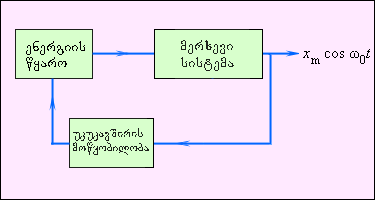
ნახ. 3.

ავტომერხევი სისტემის ფუნქციური სქემა.

 

მექანიკური თვითმერხევი სისტემის მაგალითად გამოდგემა საათიერი მექანიზმი ანკერიანი (ღუზიანი) სვლით.

ირიბი კბილანების მქონე სავალი ბორბალი მყარადაა დამაგრებული კბილანებიან დოლურასთან, რომელზეც გადადებულია ჯაჭვი საწონით (ტვირთით). ქანქარას ზედა ნაწილზე მიმაგრებულია ანკერი, ორი მაგარი მეტალური ფირფიტით, რომლებიც მოხრილია რკალის ფორმით, რომლის შესაბამისი წრეწირის ცენტრი ქანქარის ღერძის ცენტრს ემთხვევა. ხელის საათებში საწონი ზამზარითაა შეცვლილი.ბალანსატორი ასრულებს ბრუნვით რხევებს თავისი ღერძის გარშემო. საათებში მერხევ სისტემას ქანქარა ან ბალანსატორი წარმოადგენს. ენერგიის წყარო ზევით აწეული საწონი ან დაქოქილი ზამბარაა. მოწყობილობას, რომლის საშუალებითაც ხორციელდება უკუკავშირი, წარმოადგენს ანკერი, რომელის სავალ ნაწილს საშუალებას აძლევს  ერთი კბილანით შემობრუნდეს ერთი ნახევარპერიოდის განმავლობაში. უკუკავშირი ხორციელდება ანკერის სავალ ნაწილთან ურთიერთქმედებით. ქანქარის ყოველი რხევისას სავალი ბირბლის კბილანა უბიძგებს ანკერის ჩანგალს ქანქარის მოძრაობის მიმართულებით. ამგვარად, საწონის (ან ჩახვეული ზამბარის) პოტენციური ენერგია თანდათანობით, ცალკეული პორციების სახით  ქანქარას გადაეცემა.

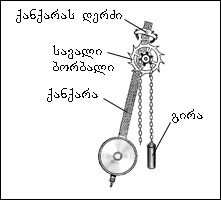
ნახ. 2.5.4.

ქანქარიანი საათის მექანიზმი.

 

მექანიკური თვითმერხევი სისტემები ფართოდაა გავრცელებული ყოფაცხობრევასა და ტექნიკაში. ავტორხევებს ასრულებენ ორთქლის მანქანები, შიგაწვის ძრავები, ელექტრული ზარი, ხემიანი სიმიანი მუსიკალური ინსტრუმენტები, ჰაერის სვეტები სასულე ინსტრუმენტებში, ხმის იოგები ლაპარაკის ან სიმღერის დროს და ა.შ.