{loadnavigation}
თანამედროვე შეხედულებით ელექტრული მუხტები არ მოქმედებენ ერთმანეთზე უშუალოდ (შეხებით). ყოველი დამუხტული სხეული გარემომცველ სივრცეში ქმნის ელექტრულ ველს. ეს ველი ძალით მოქმედებს მეორე დამუხტულ სხეულზე. ელექტრული ველის ძირითადი თვისება ელექტრულ მუხტზე გარკვეული ძალით მოქმედებაში მდგომარეობს. ამგვარად, დამუხტული სხეულებს ურთიერთქმედება ხორციელდება არა მათი უშუალო ზემოქმედებით ერთმანეთზე, არამედ მათი გარემომცველი ელექტრული ველის საშუალებით.
დამუხტული სხეულის გარემომცველი ელექტრული ველის შესწავლა შესაძლებელია ე.წ. სასინჯი მუხტის საშუალებით, რომელიც სიდიდით მცირე წერტილოვან მუხტს წარმოადგენს და არ იწვევს გამოსაცდელი მუხტების საგრძნობ გადანაწილებას.
ელექტრული ველის რაოდენობრივი განსაზღვრისათვის შემოტანილია ძალითი მახასიათებელი - ელექტრული ველის დაძაბულობა.
ელექტრული ველის დაძაბულობა ეწოდება ფიზიკურ სიდიდეს, რომელიც ტოლია ველის მიერ სივრცის მოცემულ წერტილში მოთავსებულ დადებით საცდელ მუხტზე მოქმედი ძალის ფარდობისა ამ მუხტის სიდიდესთან:
\(\vec{E}=\frac{\vec{F}}{q}.\)
ელექტრული ველის დაძაბულობა ვექტორული ფიზიკური სიდიდეა. \(\vec{E}\) ვექტორის მიმართულება სივრცის ყოველ წერტილში ემთხვევა დადებით საცდელ მუხტზე მომქმედი ძალის მიმათულებას.
უძრავი და დროში უცვლელი მუხტების ელექტრულ ველებს ელექტროსტატიკური ეწოდება. ბევრ შემთხვევაში ამ ველის სახელს სიმოკლისათვის ზოგადი ტერმინით - ელექტრული ველით ცვლიან.
თუ საცდელი მუხტის საშუალებით იკვლევენ რამოდენიმე დამუხტული სხეულის მიერ შქმნილ ელექტრულ ველს, ტოლქმედი ძალა საცდელ მუხტზე თითოეული დამუხტული სხეულის მხრიდან მომქმედი ძალების გეომეტრიული ჯამის ტოლი გამოდის. აქედან გამომდინარე, მუხტების სისტემის მიერ სივრცის მოცემულ წერტილში შექმნილი ელექტრული ველის დაძაბულობა ამ მუხტების მიერ ამავე წერთილში ცალ-ცალკე შექმნილი ელექტრული ველის დაძაბულობების ვექტორული ჯამის ტოლია:
\(\vec{E}=\vec{E_{1}}+\vec{E_{2}}+....\)
ელექტრული ველის ამ თვისებას სუპერპოზიციის პრინციპს უწოდებენ.
კულონის კანონის თანახმად Q წერტილოვანი მუხტის მიერ მისგან r მანძილზე შექმნილი ელექტრული ველის დაძაბულობა მოდულით ტოლია:
\(E=\frac{1}{4\pi\varepsilon_{0}}\cdot\frac{Q}{r^{2}}.\)
ამ ველს კულონის ველს უწოდებენ. კულონის ველში \(\vec{E}\) ვექტორის მიმართულება Q მუხტის ნიშანზეა დამოკიდებული: თუ Q > 0, მაშინ \(\vec{E}\) ვექტორი მიმართულია რადიუსის გასწვრივ მუხტიდან, და თუ Q < 0,მაშინ \(\vec{E}\) ვექტორი მიმართულია მუხტისკენ.
ელექტრული ველის თვალსაჩინო წარმოდგენისათვის იყევებენ ძალწირებს. ისინი ისეა გატარებული, რომ \(\vec{E}\) ვექტორის მიმართულება ყოველ წერტილში ემთხვა ძალწირების მხებს (ნახ. 1). ელექტრული ველის ძალწირებით გამოსახვისას მათი სიხშირე დაძაბულობის ვექტორის მოდულის პროპორციული უნდა იყოს.

ნახ. 1.
ელექტრული ველის ძალწირები.
დადებითი და უარყოფითი წერტილოვანი მუხტების კულონის ველის ძალხაზები გამოსახულია ნახ. 2-ზე. რადგანაც მუხტების ნებისმიერი სისტემის მიერ შექმნილი ელექტროსტატიკური ველი შეიძლება წარმოვადგინოთ, როგორც წერტილოვანი მუხტების კულონის ველების სუპერპოზიცია, ნახ. 2-ზე გამოსახული ველები შეიძლება განვიხილოთ, როგორც ნებისმიერი ველის ელემენტარული სტრუქტურურლი ერთეულები („აგურები“).
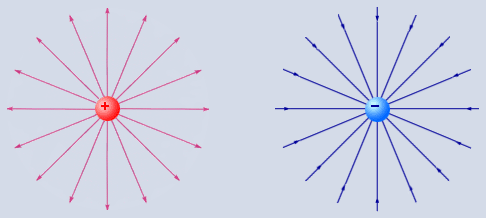
ნახ. 2.
კულონის ველების ძალწირები.
Q წერტილოვანი მუხტის კულონის ველი მოსახერხებელია ჩაიწეროს ვექტორული სახით. ამისათვის უნდა გავავლოთ \(\vec{r}\) რადიუს-ვექტორი Q მუტიდან დაკვირვების წერტილისაკენ. მაშინ, როცა Q > 0, \(\vec{E}\) ვექტორი პარალელურია \(\vec{r}\)-ს, ხოლო Q < 0, მაშინ \(\vec{E}\) ვექტორი ანტიპარალელურია \(\vec{r}\)-ს. ე.ი. შეიძლება ჩაიწეროს:
\(\vec{E}=\frac{1}{4\pi\varepsilon_{0}}\cdot\frac{Q}{r^{3}}\vec{r},\)
სადაც r - \(\vec{r}\) რადიუს-ვექტორის მოდულია.
ველების სუპერპოზიციის პრინციპის მაგალითად ნახ. 3-ზე გამოსახულია ელექტრული დიპოლის - ერთმანეთისაგან l მანძილზე განლაგებული ორი მოდულით ტოლი და სხვადასხვა ნიშნიანი q და –q მუხტების სისტემის, ძალწირები.

ნახ. 3.
დიპოლის ელექტრული ველის ძალხაზები \(\vec{E}=\vec{E_{1}}+\vec{E_{2}}.\)
ელექრტული დიპოლის მნიშვნელოვან მახასიათებელს წარმოადგენს ე.წ. დიპოლური მომენტი \(\vec{p}\):
\(\vec{p}=\vec{l}q,\)
სადაც \(\vec{l}\) - უარყოფითი მუხტიდან დადებითისაკენ მიმართული ვექტორია, მოდულით \(|\vec{l}|=l.\) . დიპოლი შეიძლება მრავალი მოლეკულის ელექტრულ მოდელად იქნეს გამოყენებული.
ელექტრული დიპოლს აქვს მომენტი, მაგალითად, წყლის ნეიტრალურ მოლეკულას (H2O), რადგანაც წყალბადის ორი ატომის ცენტრები განლაგებული არ არის ერთ სწორ ხაზზე ჟანგაბაგის მოლეკულის ცენტრთან, არამედ 105° გარადუსიანი კუთხით (ნახ. 4). წყლის მოლეკულის დიპოლური მომენტი p = 6,2·10–30 კალ · მ.

ნახ. 4.
წყლის მოლეკულის დიპოლური მომენტი
ელექტროსტატიკის მრავალ ამოცანეში საჭიროა მუხტაბის გარკვეული განაწილებისათვის (განლაგებისათვის) განისაზღვროს \(\vec{E}\) ელექტრულლი ველი. ვთქვათ, მაგალითად, საჭიროა გრძელი ერთგვაროვნად დამუხტული ძაფის ელექტრული ველის პოვნა (ნახ. 5) მისგან R მანძილზე.
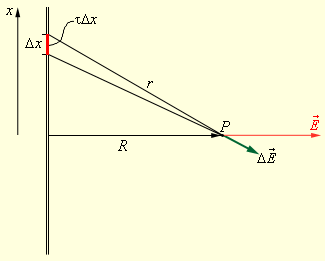
ნახ. 5.
დამუხტული ძაფის ელექტრული ველი
P დაკვირვების წერტილში ველი შეიძლება წარმოვადგინოთ ძაფის მცირე Δx ელემენტების კულონის ძალების სუპერპოზიციის სახით, რომელთა მუხტები τΔx-ის ტოლია, სადაც τ - ძაფის სიგრძის ერთეულის მუხტია. ამოცანა დაიყვანება ელემენტარული \(\Delta\vec{E}\) ველების აჯამვაზე (ინტეგრირებაზე). ველის ტოლქმედი ტოლია
\(E=\frac{\tau}{2\pi\varepsilon_{0}R}.\)
\(\vec{E}\) ვექტორი ყველგან მიმართულია \(\vec{R}\) რადიუსის გასწვრივ. ეს ამოცანის სიმეტრიიდან გამომდინარეობს. უკვე ეს მარტივი მაგალითი გვიჩვენებს, რომ მუხტების მოცემული განაწილებისას ველის განსაზღვრის პირდაპირ გზას მივყავართ რთულ მათემატუკურ გათვლებთან. გაუსის თეორემის გამოყენებით, რომელიც ელექტრული ველის ფუნდამენტურ თვისებას გამოსახავს, ზოგიერთ შემთხვევაში შეიძლება საგრძნობლად გავამარტივოთ გამოთვლები.
{loadnavigation}
ნიუტონის მექანიკაში სხეულის გრავიტაციული მასის ცნების მსგავსად, ელექტროდინამიკაში მუხტის ცნება პირველად, ძირითად ცნებას წარმოადგენს.
ელექტრული მუხტი ფიზიკური სიდიდეა, რომელიც ნაწილაკების ან სხეულების ელექტრომაგნიტურ ურთიერთქმედების უნარს ახასიათებს.
ელექტრულ მუხტს, ჩვეულებრივ, q ან Q ასოებით აღნიშნავენ.
ყველა ცნობილი ექპერიმენტული ფაქტის ერთობლიობა საშუალებას იძლევა გავაკეთოდ შემდეგი დასკვნა:
- არსებობს ორი სახის მუხტი, რომლებსაც პირობითად დადებითს და უარყოფის უწოდებენ.
- მუხტები შეიძლება ერთი სხეულიდან მეორეზე გადაეცეს (მაგალითად, უშუალო კონტაქტისას). სხეულის მასისგან განსხვავებით ელექტრული მუხტი არ წარმოადგენს მოცემული სხეულის განუყოფელ თვისებას. ერთი და იგივე სხეულს სხვადასხვა პირობებში შეიძლება სხვადასხვა მუხტი ჰქონდეს.
- ერთსახელიანი მუხტები განიზიდებიან, სხვადასხვა სახელიანი მიხტები – მიიზიდებიან. ამაშიც ასევე ვლინდება პრინციპული განსხვავება ელექტრომაგნიტურ და გრავიტაციულ ძალებს შორის. გრავიტაციული ძალები ყოველთვის მიზიდულობის ძალებია.
ბუნების ერთ-ერთ ფუნდამენტურ კანონს ექსპერიმენტულად დადგენილი ელექტრული მუხტის შენახვის კანონი წარმოადგენს.
იზოლირებულ სისტემაში ყველა სხეულის მუხტების ალგებრული ჯამი უცვლელი რჩება:
q1 + q2 + q3 + ... +qn = const.
ელექტრული მუხტის შენახვის კანონი ამტკიცებს, რომ ჩაკეტილ სისტემაში არ შეიძლება იქნეს დაკვირვებული ერთიდაიგივე ნიშნიანი მუხტის დაბადების ან გაქრობის პროცესები.
თანამედროვე თვალსაზრისით, მუხტის მატარებლებს ელემენტარული ნაწილაკები წარმოადგენან. ყველა ჩვეულებრივი სხეული შედგება ატომებისაგან, რომლის შემადგენლობაშიც შედის დადებითად დამიხტული პროტონები, უარაყოფითად დამუხტული ელექტრონები, და ნეიტრალური ნაწილაკები – ნეიტრონები. პროტონები და ნეიტრონები ატომის ბირთვის შემადგენლობაში შედიან, ელექტრონები ატომის ელექტრონულ გარსს ქმნიან. პროტონისა და ელექტრონის ელექტრული მუხტები მოდულით ზუსტად ერთნაირია და ელემენტარული e მუხტის ტოლია.
ნეიტრალური ატომის ბირთვში პროტონების რიცხვი ტოლია გარსში ელექტრონების რიცხვისა. ამ რიცხვს ატომურ რიცხვს უწოდებენ. მოცემული ნივთიერების ატომს შეუძლია დაკარგოს ერთი ან რამდენიმე ელექტრონი ან მიიერთოს ზედმეტი ელექტრონი. ასეთ შემთხვევებში ნეიტრალური ატომი დადებითად ან უარყოფითად დამუხტულ იონად იქცევა.
მუხტი ერთი სხეულიდან მეორეს მხოლოდ ელემენტარული მუხტის მთელი რიცხვის შემცველი პორციებით გადაეცემა. ამგვარად, სხეულის ელექტრული მუხტი – დისკრეტული სიდიდეა:
\(q=\pm ne\; (n=0,1,2,....).\)
ფიზიკურ სიდიდეებს, რომლებსაც შეუძლიათ მხოლოდ დისკრეტული მნიშვნელობების მიღება დაქვანტულს უწოდებენ. ელემენტარული მუხტი ელექტრული მუხტის ქვანტს წარმოადგენს (უმცირესი პორცია). უნდა აღინიშნოს, რომ ელემენტარული ნაწილაკების თანამედროვე ფიზიკაში ვარაუდობენ ე. წ. კვარკების არსებობას – ნაწილაკები
\(\pm\frac{1}{3}e\) \(\pm\frac{2}{3}e\)
წილადური მუხტით, მაგრამ ჯერჯერობით თავისუფალ მდგომარეობაში კვარკები დაკვირვებული არაა.
ჩვეულებრივ ლაბორატორიულ ცდებში ელექტრული მუხტის აღმოსაჩენად და გასაზომად იყენებენ ელექტრომეტრს – ხელსაწყოს, რომელიც შედგება მეტალური ღეროსა და ჰორიზონტული ღერძის გარშემო მბრუნავი ისრისაგან (ნახ. 1).
ღერო ისრით, იზოლირებულია მეტალის კორპუსიდან. დამუხტულ სხეულთან ელექტრომეტრის ღეროსთან შეხებისას, ერთი ნიშნის მქონე მუხტი ნაწილდება ღეროსა და ისარზე. ელექტრული განზიდულობის ძალები იწვევენ ისრის გარკვეული კუთხით მობრუნებას, რომლის მიხედვითაც შეიძლება ვიმსჯელოთ ელექტრომეტრზე გადაცემული მუხტის შესახებ.
.gif)
ნახ. 1.
მუხტის გადატანა დამუხტული სხეულიდან ელექტრომეტრზე.
ელექტრომეტრი საკმაოდ უხეში ხელსაწყოა; ის მუხტების ურთიერთქმედების ძალების გაზომვის საშუალებას არ იძლევა. უძრავი მუხტების ურთიერთქმედების კანონი აღმოაჩინა ფრანგმა ფიზიკოსმა შ.კულონმა 1785 წელს. თავის ცდებში კულონი ზომავდა დამუხტული ბურთულების მიზიდვისა და განზიდვის ძალებს მის მიერვე კონსტრუირებული ხელსაწყოს – გრეხითი სასწორის საშუალებით (ნახ. 2), რომელიც ძალიან დიდი მგრძნობიარობით გამოირჩევა. ასე მაგალითად, სასწორის ბალანსი 1°-ით მობრუნდება 10–9 ნ რიგის ძალის მოქმედებით.
გაზომვის იდეა ემყარებოდა კულონის ბრწყინვალე ეჭვს იმის შესახებ, რომ თუ დამუხტულ ბურთულას შევახებთ ზუსტად ისეთივე დაუმუხტავ ბურთულას, მაშინ პირველის მუხტი მათ შორის ზუსტად თანაბრად განაწილდება. ამგვარად, ნაჩვენები იყო ბურთულას ორჯერ, სამჯერ და ა.შ. მუხტის გაზომვის გზა. კულონის ცდებში ურთიერთქმედება იზომებოდა ისეთ ბურთულებს შორის რომელთა ზომები გაცილებით ნაკლები იყო მათ შორის მანძილზე. ასეთ დამუხტულ სხეულებს წერტილოვან მუხტებს უწოდებენ.
წერტილოვანი მუხტი ეწოდება დამუხტულ სხეულს, რომლის ზომების უგულებელყოფა შესაძლებელია მოცემული ამოცანის პორობებში.

ნახ. 2.
კულონის ხელსაწყო
.gif)
ნახ. *3.
ერთსახელიანი და სხვადასხვა სახელიანი მუხტების ურთიერთქმედების ძალები
მრავალრიცხოვანი ცდების საფუძველზე კულონმა გამოიყვანა შემდეგი კანონი:
უძრავი მუხტების ურთიერთქმედების ძალები პირდაპირ პროპორციულია მუხტების მოდულების ნამრავლისა დაუკუპრორორციულია მათ შორის მანძილის კვადრატისა:
\(F=k\frac{|q_{1}|\cdot |q_{2}|}{r^{2}}.\)
ურთიერთქმედების ძალები ემორჩილებიან ნიუტონის მესამე კანონს: \(\vec{F_{1}}=-\vec{F_{2}}.\) ისინი განზიდვის ძალები არიან ერთნაირ ნიშნიანი მუხტების შემთხვევაში და მიზიდულობისა - სხვადასხვა ნიშნიანი მუხტების შემთხვევაში (ნახ. 3). უძრავი მუხტების ურთიერთქმედებას ელექტროსტატიკურ ან კულონურ ურთიერთქმედებას უწოდებენ. ელექტროდინამიკის განყოფილება რომელიც კულონურ ურთიერთქმედებას სწავლობს ელექტროსტატიკა ეწოდება.
კულონის კანონი სამართლიანია წერტილოვანი დამუხტული სხეულებისათვის. პრაქტიკულად კულონის კანონი კარგად სრულდება, თუ დამუხტული სხეულებოს ზომები ბევრად ნაკლებია მათ შორის მანძილზე.
კულონის კანონში პროპორციულობის k კოეფიციენტი დამოკიდებულია ერთეულების სისტემის შერჩევაზე. საერთაშორისო სი სისტემაში მუხტის ერთეულად მიღებულია კულონი (კ).
კულონი მუხტია, რომელიც სადენის განივკვეთში გადის ერთი წამის განმავლობაში, ერთი ამპერი დენის ძალის დროს. დენის ძალის ერთეული (ამპერი) სი სისტემაში, სიგრძის, დროის და მასის ერთეულიბთან ერთად, ძირითად ერთეულს წარმოადგენს.
k კოეფიციენტი სი სისტემაში ჩვეულებრივ ჩაიწერება შემდეგი სახით:
\(k=\frac{1}{4\pi \varepsilon_{0}},\)
სადაც \(\varepsilon_{0}=8,85\cdot 10^{-12}\) კლ2/ნ.მ2– ელექტრული მუდმივაა.
სი სისტემაში ელექტრული მუხტი e ტოლია:
ცდა უჩვენებს, რომ კულონური ურთიერთქმედების ძალები სუპერპოზიციის პრინციპს ემორჩილება.
თუ დამუხტული სხეული ერთდროულად რამდენიმე დამუხტულ სხეულთან ურთიერთქმედებს, მაშინ მოცემულ სხეულზე მომქმედი ტოლქმედი ძალა ტოლია ყველა სხვა სხეულის მიერ ამ სხეულზე მომქმედი ძალების ვექტორული ჯამისა.
ნახ. 4 ხსნის სუპერპოზიციის პრინციპს სამი დამუხტული სხეულის ელექტროსტატიკური ურთიერთქმედების საშუალებით.
.gif)
ნახ. 4.
ელექტროსტატიკური ძალების სუპერპოზიციის პრინციპი \(\vec{F_{1}}=\vec{F_{21}}+\vec{F_{31}}\); \(\vec{F_{2}}=\vec{F_{12}}+\vec{F_{32}}\); \(\vec{F_{3}}=\vec{F_{13}}+\vec{F_{23}}.\)
სუპერპოზიციის პრინციპი ბუნების ფუნდამენტურ კანონს წარმოადგენს. მაგრამ, როცა ლაპარაკია სასრული ზომების მქონე დამუხტულ სხეულებზე, მისი გამოყენაბა გარკვეულ სიფრთხილეს მოითხოვს (მაგალითად, ორი გამტარი დამუხტული ბირთვი 1 და 2). თუ ორი გამტარი დამუხტული ბირთვისაგან შემდგარ სისტემასთან მივიტანთ დამუხტულ მესამე ბირთვს, მაშინ 1 და 2 ბირთვებს შორის ურთიერთქმედება მუხტების გადანაწილების გამო შეიცვლება.
სუპერპოზიციის პრინციპი ამტკიცებს, რომ ყველა სხეულზე მუხტის განსაზღვრული (ფიქსირებული) განაწილებისას ელექტული ურთიერთქმედება ნებისმიერ ორ სხეულს შორის არ არის დამოკიდებული სხვა დამიხტული სხეულების არსებობაზე.
{loadnavigation}
მრავალი ფიზიკური მოვლენა, რომელიც ბუნებასა და ჩვენს გარემომცველ ცხოვრებაში დაიკვირვება, შეუძლებელია აიხსნას მექანიკის, მოლეკულარულ-კინეტიკური თეორიის და თერმოდინამიკის კანონებით. ამ მოვლენებში თავს იჩენს გარკვეული მანძილით დაშორებულ სხეულებს შორის მომქმედი ძალები, რომლებიც არაა დამოკიდებული ურთიერთქმედი სხეულების მასებზე, და ე.ი. არ წარმოადგენენ გრავიტაციულ ძალებს. ამ ძალებს ელექტრომაგნიტურ ძალებს უწოდებენ.
ელექტრომაგნიტური ძალების არსებობა ჯერ კიდევ ძველი ბერძნებისთვის იყო ცნობილი. მაგრამ სისტემატური, რაოდენობრივი შესწავლა იმ ფიზიკური მოვლენებისა სადაც ვლინდება სხეულების ელექტრული ურთიერთქმედება მხოლოდ XVIII საუკუნის ბოლოს დაიწყო. მრავალი მეცნიერის ძალისხმევით XIX საუკუნეში დასრულდა ელექტრული და მაგნიტური მოვლენების შემსწავლელი თანმიმდევრული მეცნიერების შექმნა. ეს მეცნიერება ფიზიკის ერთ-ერთ მნიშვნელოვან ნაწილს წარმოადგენს, და მას ელექტროდინამიკა ეწოდება.
ელექტროდინამიკის შესწავლის ძირითად ობიექტებს ელექტრული მუხტებისა და დენების მიერ წარმოქმნილი ელექტრული და მაგნიტური ველები წარმოადგენენ.
{loadnavigation}
თერმოდინამიკის პირველი კანონი - სითბური პროცესებისათვის ენერგიის შენახვის კანონი - ადგენს კავშირს სისტემის მიერ მიღებულ \(Q\) სითბოს რაოდენობას და მისი შინაგანი ენერიის \(\Delta U\) ცვლილებასა და გარე სხეულებზე შესრულებულ მუშაობას \(A\) შორის:
\(Q=\Delta U+A.\)
ამ კანონის თანახმად, ენერგია არც შეიძლება წარმოიქმნეს და არც განადგუურდეს: იგი ერთი სისტემიდან გადაეცემა მეორეს და ერთი ფორმის ენერგიიდან გარდაიქნმება მეორეში. პროცესები, რომლებიც თერმოდინამიკის პირველ კანონს დაარღვევდნენ არასოდეს დაკვირვებულა. ნახ. 1-ზე გამოსახულია მოწყობილობა რომელიც პირველი კანონითაა აკრძალული.
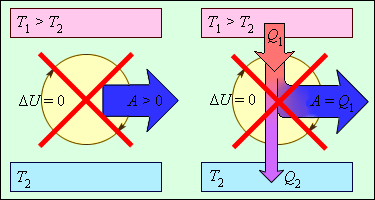
ნახ. 1.
პირველი კანონით აკრძალული ციკლურად მომუშავე სითბური მანქანები.
თერმოდინამიკის პირველი კანონი ადგენს სითბური პროცესების მიმართულებას. მაგრამ, როგორც გამოცდილება უჩვენებს. მრავალი სითბური პროცესი შეიძლება მიმდინარეობდეს ერთი მიმართულებით. ასეთ პროცესებს შეუქცევადს უწოდებენ. მაგალითად, ორი სხეულის სითბური კონტაქტისას სითბური ნაკადი ყოველთვის მიმართულია უფრო ცხელიდან ცივისაკენ. არასოდეს დაიკვირვება სითბოს თვითნებური გადაცემა უფრო დაბალი ტემპერატურის სხეულიდან უფრო მაღალი ტემპერატურისაზე. ე.ი. თბოგაცვლის პროცესი სასრული ტემპერატურული სხვაობისას შეუქცევადი პროცესია.
შექცევადი ეწოდება ერთი წონასწორული მდგომარეობიდან მეორეში გადასვლის პროცესებს, რომლებიც შესაძლებელია შუალედური წონასწორული მდგომარეობების იგივე მიმდევრობით საწიმააღმდეგო მიმართულებითაც განხორციელდეს. ამასთან სისტემა და გარემომცველი სხეულები ბრუნდებიან საწყის მდგომარეობაში.
პროცესები რომლის მიმდინარეობის განმავლობაში სისტემა ყოველთვის წონასწორულ მდგომარეობაში რჩება კვაზისტატისტიკურს უწოდებენ. ყველა კვაზისტატისტიკური პროცესი შექცევადია.
თუ სითბური მანქანის მუშა სხეული ისეთ სითბურ რეზერვუართან კონტაქტში იმყოფება, რომლის ტემპერატურაც თბოგაცვლის პროცესში უცვლელი რჩება, ერთადერთ შექცევად პროცესს იზოთერმული კვაზისტატისტიკური პროცესი წარმოადგენს, რომელიც მუშა სხეულისა და რეზერვუარს შორის უსასრულოდ მცირე ტემპერატურული სხვაობის პირობებში მიმდინარეობს. ორი განსხვავებული ტემპერატურის მქონე რეზერვუარის არსებობის შემთხვევაში პროცესი შეიძლება წარიმართოს შებრუნებულად ორ იზოლირებულ უბანზე. რადგანაც ადიაბატური პროცესიც შეიძლება მიდიოდეს ორივე მიმართულებით (ადიაბატური შეკუმშვა და ადიაბატური გაფართოება), ამიტომ ორი იზოთერმისა და ორი ადიაბატისგან შემდგარი წრიული პროცესი (კარნოს ციკლი) წარმოადგენს ერთადერთ შექცევად წრიულ პროცესს, რომლის დროსაც მუშა სხეული კონტაქტშია მხოლოდ ორ სითბურ რეზერვუართან. ყველა სხვა ციკლური პროცესი, რომელიც ორი სითბური რეზერვუარის პირობებში მიმდინარეობს შეუქცევადია.
მექანიკური მუშაობის სხეულის შინაგან ენერგიად გარდაქმნის პროცესები შეუქცევადია ხახუნის, აირებსა და სითხეებში დიფუზიური პროცესების, წნევათა სხვაობით გამოწვეული აირის შერევის (გადაადგილების) და სხვა პროცესების არსებობის გამო. ყველა რეალური პროცესი შეუქცევადია, მაგრამ ისინი შეიძლება საკმაოდ უახლოვდებოდეს შექცევად პროცესებს. შეუქცევადი პროცესები რეალური პროცესების იდეალიზაციას წარმოადგენს.
თერმოდინამიკის პირველ კანონს არ შეუძლია განასხვაოს შექცევადი პროცესი შეუქცევადიდან. ის თერმოდინამიკური პროცესისაგან უბრალოდ ენერგეტიკულ ბალანს მოითხოვს და არაფერს ამბობს იმის შესახებ, შესაძლებელია თუ არა ასეთი პროცესი. თავისთავად მიმდინარე პროცესის მიმართულებას ადგენს თერმოდინამიკის მეორე კანონი. ის შეიძლება ჩამოყალიბდეს გარკვეული სახის თერმოდინამიკური პროცესების აკრძალვის ფორმით.
ინგლისელმა ფიზიკოსმა კელვინმა 1851 წ. მეორე კანონი შემდეგი სახით ჩამოაყალიბა:
ციკლურად მომქმედ სითბურ მანქანაში შეუძლებელია პროცესი, რომლის ერთადერთი შედეგი იქნებოდა ერთადერთი სითბური რეზერვუარიდან მიღებული მთელი სითბოს რაოდენობის მექანიკურ მუშაობად გარდაქმნა.
ჰიპოტეტურ სითბურ მანქანას, რომელშიც შეიძლება მიმდინარეობდეს ასეთი პროცესი, მეორე სახის მუდმივ ძარავას უწოდებენ. დედამიწის პირობებში ასეთი მანქანას შეეძლო სითბური ენერგია აეღო, მაგალითად, მსოფლიო ოკიანიდან და მთლიანად გარდაექმნა მუშაობად. მსოფლიო ოკეანეში წყლის მასა დაახლოებით 1021კგ-ს წარმოადგენს და მისი ერთი გრადუსით გაციებისას გამოიყოფოდა უზარმაზარი ენერგია (≈ 1024 ჯ), რაც 1017კგ ნახშირის სრული დაწვის ექვივალენტურია. დედამიწაზე ყოველწლიურად გამომუშავებული ენერგია დაახლოებით 104-ჯერ ნაკლებია. ამიტომ მეორე სახის მუდმივი ძრავა ადამიანისათვის არანაკლებ მიმზიდველი იქნებოდა პირველი სახის მუდმივ ძრავაზე, რომელიც თერმოდინამიკის პირველი კანონითაა აკრძალული.
გერმანელმა ფიზიკისმა კლაუზიუსმა თერმოდინამიკის მეორე კანონს სხვა ფორმულირება მისცა:
შეუძლებელია პროცესი, რომლის ერთადერთ შედეგი შეიძლება იყოს ენერგიის გადაცემა დაბალი ტემპერატურის სხეულსა და უფრო მაღალი ტემპერატურის სხეულს შორის თბოგაცვლის შედეგად.
ნახ. 2-ზე გამოსახულია თერმოდინამიკის მეორე კანონით აკრძალული პროცესები. ეს პროცესები თერმოდინამიკის მეორე კანონის ორ სხვადასხვა ფორმულირებას შეესაბამება.
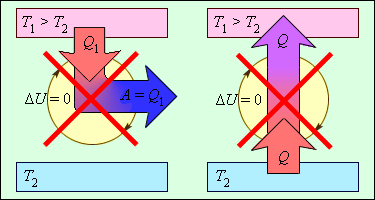
ნახ. 3.12.2.
პროცესები, რომლებიც არ ეწინაღმდეგებიან თერმოდინამიკის პირველ კანონს, მაგრამ აკრძალილია მეორე კანონით: 1 - მეორე სახის მუმივი ძრავი; 2 - (იდეალური გამაციებელი მანანა)
უნდა აღინიშნოს, რომ თერმოდინამიკის მეორე კანონის ორივე განმარტება ექვივალენტურია. თუ დაუშვებთ, მაგალითად, რომ სითბო თბოგაცვლისას თავისთავად (ე.ი. დამატებითი მუშაობის დახარჯვის გარეშე) გადადის ცივი სხეულიდან ცხელზე, შეიძლება მივიდეთ დასკვნამდე, რომ მეორე სახის მუდმივი ძრავის შექმნა შესაძლებელია. სინამდვილეში, ვთქვათ რეალური სითბური მანქანა გამათფობელიდან ღებულობს Q1 სითბოს რაოდენობას და გადასცემს გამაციებელს Q2 სითბოს რაოდენობას. ამ დროს სრულდება მუშაობა A = Q1 – |Q2|. |Q2| სითბოს რაოდენობა თავისით რომ გადადიოდეს გამაციებლიდან გამაცხელებელზე, მაშინ რეალური სითბური მანქანის და იდეალური გამაციებელი მანქანის საბოლოო შედეგი იქნებოდა მუშაობად გარდაქმნა Q1 – |Q2| სითბოს იმ რაოდენობისა, რომელიც მიიღება გამაცხელებლიდან გამაციებელში რაიმე ცვლილების გარეშე. ამგვარად, რეალური სითბური მანქანის და იდეალური გამაციებელი მანქანის კომბინაცის მეორე ტიპის მუდმივი ძრავის ექვივალენტურია. ზუსტად ასევე შეიძლება ვაჩვენოთ, რომ რეალური გამაციებელი მანქანისა და მეორე ტიპის მუდმივი ძრავის კომბინაცია იდეალური გამაციებელი მანქანის ექვივალენტურია.
თერმოდინამიკის მეორე კანონი პირდაპირ კავშირშია რეალური სითბური პროცესების შეუქცევადობასთან. მოლეკულების სითბური მოძრაობის ენერგია ხარისხობრივად განსხვავდება ენერგიის ყველა სხვა სახეობიდან - მექანიკური, ელექტრული, ქიმიური და ა.შ. მოლეკულების სითბური მოძრაობის ენერგიის გარდა ნებისმიერი სახის ენერგიას შეუძლია სრულად გადაიქცეს ენერგიის ნებისმიერ სხვა სახედ, მათ შორის სითბური მოძრაობის ენერგიად. უკანასკნელს კი შეუძლია ნებისმიერ სხვა ენერგიად გარდაქმნა მხოლოდ ნაწილობრივ. ამიტომ ნებისმიერი ფიზიკური პროცესი, რომელშიც რომელიმე სახის ენერგიის გარდაქმნა ხდება მოლეკულების მოძრაობის სითბურ ენერგიად, შეუქცევად პროცესს წარმოადგენს, ე.ი. ის სრულად ვერ განხორციელდება საწინააღმდეგო მიმართულებით.
ყველა შეუქცევადი პროცესის საერთო თვისება იმაში მდგომარეობს, რომ ისინი თერმოდინამიკურად გაუწონასწორებულ სისტემაში მიმდინარეობს და ამ პროცესების შედეგად ჩაკეტილი სისტემა უახლოვდება თერმოდინამიკური წონასწორობის მდგომარეობას.
თერმოდინამიკის მეორე კანონის ნებისმიერი განმარტების საფუძველზე შეიძლება დამტკიცდეს შემდეგი მტკიცებულება, რომელიც კარნოს თეორემის სახელწოდებითაა ცნობილი:
1. გამაცხელებლისა და გამაციებლის მოცემულ ტემპერატურაზე მომუშავე სითბური მანქანის მარგი ქმედების კოეფიციენტი არ შეიძლება იყოს მეტი, ვიდრე გამაცხელებლისა და გამაციებლის იგივე ტემპერატურებზე შექცევადი კარნოს ციკლით მომუშავე სითბური მანქანის მარგი ქმედების კოეფიციენტი.
2. კარნოს ციკლით მომუშავე სითბური მანქანის მარგი ქმედების კოეფიციენტი არ არის დამოკიდებული მუშა სხეულის გვარობაზე და დამოკიდებულია მხოლოდ გამაცხელებლისა და გამაციებლის ტემპერატურებზე.
ამგვარად, კარნოს ციკლით მომუშავე სითბური მანქანის მარგი ქმედების კოეფიციენტი მაქსიმალურია.
\(\mu=1-\frac{Q_{2}}{Q_{1}}\leq\mu_{max}=\mu_{karno}=1-\frac{T_{2}}{T_{1}}.\)
ამ თანაფარდობაში ტოლობის ნიშანი შექცევად ციკლს შეესაბამება. კარნოს ციკლით მომუშავე მანქანისათვის ეს თანაფარდობა შეიძლება ჩაიწეროს შემდეგი სახით:
\(\frac{|Q_{2}|}{Q_{1}}=\frac{T_{2}}{T_{1}}\) ან \(\frac{|Q_{2}|}{T_{2}}=\frac{Q_{1}}{T_{1}}\)
რომელი მიმართულებითაც არ უნდა ხდებოდეს კარნოს ციკლეს შემოვლა (საათის ისრის მიმართულებით თუ საწინააღმდეგოდ) Q1 და Q2 სიდიდეებს ყოველთვის განსხვავებული ნიშნები აქვთ. ამიტომ შეიძლება ჩავწეროთ
\(\frac{|Q_{2}|}{T_{2}}+\frac{Q_{1}}{T_{1}}=0.\)
ამ თანაფარდობის განზოგადება შესაძლებელია ნებისმიერ ჩაკეტილ შექცევად პროცესზე, რომლის წარმოდგენაც შესაძლებელია მცირე იზოთერმული და ადიაბატური მონაკვეთების სახით (ნახ. 3).
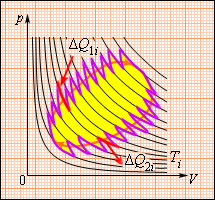
ნახ. 3.თავისთავადი შექცევადი ციკლი, როგორც მცირე იზოთერმული და ადიაბატური მონაკვეთბის მიმდევრობა
შექცევადი ციკლის სრული შემოვლისას
\(\sum\frac{\Delta Q_{i}}{T_{i}}=0\) (შექცევადი ციკლი)
სადაც ΔQi = ΔQ1i + ΔQ2i – Ti ტემპერატურის პირობებში ორ იზოთრმულ უბანზე მუშა სხეულის მიერ მიღებული სითბოს რაოდენობაა. იმისათვის რომ, ასეთი რთული ციკლი შებრუნებულად ჩავატაროთ, აუცილებელია მუშა სხეულის კონტაქტში მოყვანა Ti ტემპერატურის მქონე მრავალ რეზერვუართან. ΔQi / Ti თანაფარდობას დაყვანილ სითბოს უწოდებან. მიღებული ფორმულა უჩვენებს, რომ სრული დაყვანილი სითბო ნებისმიერ შექცევად ციკლზე ნულის ტოლია. ეს ფორმულა ახალი ფიზიკური სიდიდის შემოტანის საშუალებას იძლევა. ამ სიდიდეს ენტროპიას უწოდებენ და S-ით აღნიშნავენ (რ.კლაუზიუსი 1865 წ.). თუ თერმოდინამიკური სისტემა ერთი წონასწორული მდგომარეობიდან მეორეში გადადის, მაშინ მისი ენტროპია იცვლება. ორ მდგომარეობაში ენტროპიის მნიშვნელობათა სხვაობა იმ დაყვანული სითბოს ტოლია, რომელსაც სისტემა იღებს შექცევარი გადასვლისას ერთი მდგომარეობიდან მეორეში.
\(\Delta S=S_{2}-S_{1}=\sum_{1}^{2}\frac{\Delta Q_{i}}{T}.\)
შექცევადი ადიაბატური პროცესის დროს \(\Delta Q_{i}=0\) და ,ე.ი. ენტროპია S უცვლელი რჩება.
არაიზოლირებული სისტემის ერთი წონასწორული მდგომარეობიდან (1) მეორე წონასწორული მდგომარეობაში (2) გადასვლისას ენტროპიის გამოსახულება შეიძლება ასე ჩაიწეროს
\(\Delta S=\int_{1}^{2}\frac{dQ}{T}.\)
ენტროპია განისაზღვრება უკანასკნელი შესაკრების სიზუსტით, ისევე რორორც, მაგალითად, პოტენციური ენერგია ძალის მოქმედების ველში. ფიზიკური არსი სისტემის ორ მდგომარეობას შორის ენტროპიათა ΔS სხვაობას აქვს. რომ განისაზღვროს სისტემის ერთი მდგომარეობიდამ მეორეში შეუქცევადი გადასვლისას ენტროპიის ცვლილება უნდა იქნეს მოფიქრებული რაღაც შექცევადი პროცესი რომელიც აკავშირებს საწყის და საბოლოო მდგომარეობებს და ასეთი გადასვლის პირობებში განისაზრვროს სისტემის მიერ მიღებული დაყვანილი სითბო.
ნახ. 4 აირის „სიცარიელეში“ შეუქცევადი გაფართოების პროცესს გვიჩვენებს, რომელიც თბოგაცვლის გარეშე მიმდინარეობს. ამ პროცესში აირის მხოლოდ საწყისი და საბოლოო მდგომარეობებია წონასწორული და მათი გამოსახვა შესაძლებელია (p, V) დიაგრამაზე. ამ მდგომარეობების შესაბამისი (a) და (b) წერტილები ერთ იზოთერმაზე მდებარეობენ. ენთროპიის ΔS ცვლილების გამოთვლისათვის შეიძლება განვიხილით შექცევადი იზოთერმული გადასვლა (a)-დან (b)-ში. რადგანაც, იზოთერმული გაფართოებისას აირი იღებს გარკვეულ სითბოს რაოდენობას გარემომცველი სხეულებიდან Q > 0, შეიძლება დავასკვნათ, რომ აირის შეუქცევადი გაფართოებისას ენთროპია გაიზარდა: ΔS > 0.
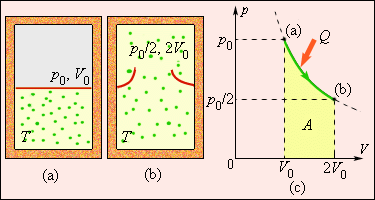
ნახ. 4.
აირის გაფართოება „სიცარიელეში“. ენთროპიის ცვლილება \(\Delta S=\frac{Q}{T}=\frac{A}{T}>0,\) სადაც A = Q – აირის მუშაობაა შქცევადი იზოთერმული გაფართოების დროს.
შეუქცევადი პროცესის მეორე მაგალითია - თბოგაცვალა ტემპერატურების სასრული სხვაობის შემთხვევაში. ნახ.5-ზე ადიაბატურ გარსში მოქცეული ორი სხეულია გამოსახული. სხეულბის საწყისი ტემპერატურები T1 და T2 < T1. თბოგაცვლისას სხეულების ტემპერატურები თანდათან თანაბრდება. უფრო თბილი სხეული გასცემს გარკვეულ რაოდენობა სითბოს, ცივი კი ღებულობს.
ცივი სხეულის მიერ მიღებული სითბო მოდულით ჭარბობს თბილი სხეულის მიერ გაცემულ სითბოს. აქედან გამომდინარეობს, რომ შეუქცევადი თბოგაცვლის პროცესის დროს ჩაკეტილ სისტემაში ენთროპიის ცვლილება ΔS > 0.
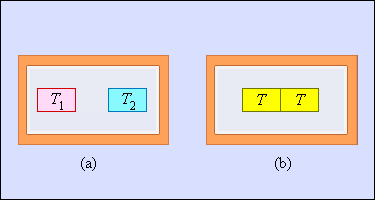
ნახ. 5.
თბოგაცვლა ტემპერატურის სასრული სხვაობისას: a – სისტემის საწყისი მდგომარეობა; b – სისტემის საბოლოო მდგომარეობა. ენთროპიის ცვლილება ΔS > 0
ენთროპიის ზრდა იზოლირებულ თერმოდინამიკურ სისტემებში ყველა თვითნებურად მიმდინარე შეუქცევადი პროცესის საერთო მახასიათებელია. იზოლირებულ თერმოდინამიკურ სისტემებში შექცევად პროცესებში ენთროპია არ იცვლება: ΔS ≥ 0.
ამ თანაფარდონას ენთროპიის ზრდის კანონს უწოდებენ.
თერმოდინამიკურად იზოლირებულ სისტემებში მიმდინარე ნებისმიერი პროცესისას ენთროპია ან უცვლელი რჩება, ან იზრდება.
ამგვარად, ენთროპია თვითნებურად მიმდინარე პროცესების მიმართულებაზე მიუთითებს. ენთროპიის ზრდა მიუთითებს სისტემის თერმოდინამიკურ წონასწორობასთან მიახლოებაზე. წონასწორობის მდგომარეობაში ენტროპია მაქსიმალურ მნიშვნელობას ღებულობს. ენპროპიის ზრდის კანონი შეიძლება თერმოდინამიკის მეორე კანონის კიდევ ერთ ფორმულირებად ჩაითვალოს.
1878 წ. ბოლცმანმა ენთროპიის ცნების ალბათური განმარტება გააკეთა. მან შესთავაზა ენთროპია განეხილათ როგორც ჩაკეტილ თერმოდინამიკური სისტემაში სტატისტიკური ქაოსის საზომი. ჩაკეტილ სისტემაში ყველა თვითნებურად მიმდინარე პროცესი, რომელიხ სისტემას წონასწორობის მდგომარეობასთან აახლოებს და თან ახლავს ენთროპიის ზრდა, მიმართულნი არიან მდგომარეობის ალბათობის ზრდისაკენ.
ნაწილაკების დიდი რიცხვის შემცველი მაკროსკოპული სისტემის ნებისმიერი მდგომარეობა შეიძლება ბრავალი ხერხით განორციელდეს. სისტემის მდგომარეობის თერმოდინამიკური ალბათობა - არის იმ ხერხების რცხვი, რომლებითაც შეიძლება გახორციელდეს მაკროსკოპული სისტემის მოცემული მდგომარეობა, ან იმ მიკრომდგომარეობების რიცხვი, რომლებიც ახორციელებენ მოცემულ მაკრომდგომარეობას. განმარტების მიხედვით თერმოდინამიკური ალბათობა W >> 1.
მაგალითად, თუ ჭურჭელში 1 მოლი აირია, შესაძლებელია მოლეკულების ჭურჭლის ორ ნახევარში განთავსების ხერხების ძალიან დიდი რიცხვი N: \(N=2^{N_{A}}\) სადაც \(N_{A}\) - ავოგადროს რიცხვია. ყოველი მათგანი მიკრომდგომარეობას წარმოადგენს. მხოლოდ ერთი მიკრომდგომარეობა შეესაბამება იმ შემთხვევას, როცა მოლეკულები თავს მოიყრიან ჭურჭლის ერთ (მაგ., მარჯვენა) ნახევარში. ასეთი შემთხვევის ალბათობა პრაქტიკულად ნულის ტოლია. მიკრომდგომარეობის ყველაზე დიდი რიცხვი შეესაბამება წონასწორულ მდგომარეობას, როცა მოლეკულები თანაბრადაა განაწილებული ჭურჭლის მთელ მოცულობაში. ამიტომ წონასწორული მდგომარეობა ყველაზე ალბათურია. მეორე მხრივ წონასწორული მდგომარეობა თერმოდინამიკურ სისტემაში ყველაზე მაქსიმალური ქაოსის მდგომარეობას და მაქსიმალურ ენტროპიას წარმოადგენს.
ბოლცმანის თანახმად,სისტემის ენთროპია S და თერმოდინამიკური ალბათობა W ერთმანეთთან შემდეგნაირადაა დაკავშირებული:
S = k ln W,
სადაც k = 1,38·10–23 ჯ/კ – ბოლცმანის მურმივაა. ამგვარად, ენთროპია განისაზღვრება იმ მიკრიმდგომარეობების რიცხვის ლოგარითმით, რომელთა საშუალებითაც შეიძლება განხორციელდეს მაკრომდგომარეობა. ე.ი. ენთროპია შეიძლება განხილულ იქნეს თერმოდინამიკური სისტემების მდგომარეობების ალბათობათა ზომად (საზომი).
თერმოდინამიკის მეორე კანონის ალბათური ინტერპრეტაცია შესაძლებელს ხდის სისტემის სპონტანურ (თავისთავად) გადახრას თერმოდინამიკური წონასწორობიდან. ასეთ გადახრებს ფლუქტუაციებს უწოდებენ. ნაწილაკების დიდი რიცხვის შემცველ სისტემებში წონასწორობის მდგომარეობიდან მიშვნელოვანი გადახრა ნაკლებად ალბათურია.
