{loadnavigation}
B მაგნიტურ ველში მდებარე \(\Delta l\) სიგრძის გამტარზე, რომელშიც \(I\) ძალის დენი გადის, მომქმედი ამპერის ძალა
\(F=IB\Delta l\sin \alpha\)
შეიძლება გამოისახოს ისეთი ძალების საშუალებით, რომლების მუხტის ცალკეულ მატარებლებზძე მოქმედებენ.
ვთქვათ გამტარში თავისუფალი მუხტის მატარებლების კონცენტრაცია n-ია, ხოლო q – მატარებლის მუხტია. მაშინ ნამრავლი \(qnvS\) , სადაც \(v\) – გამტარში მატარებლების მოწესრიგებული მოძრაობის სიჩქარის სიდიდეა, ხოლო S – გამტარის განიკვეთის ფართობია, გამტარში გამავალი დენის ტოლია:
\(I=qnvS\).
ამპერის ძალის გამოსახულება შეიძლება ასე ჩაიწეროს:
\(F=qnS\Delta lvB\sin \alpha\).
რადგანაც \(\Delta l\) სიგრძის და S განივკვეთის გამტარში თავისუფალი მუხტის მატარებლების სრული რიცხვი N ტოლია \(nS\Delta l\), ამიტომ ერთ დამუხტულ ნაწილაკზე მომქმედი ძალა ტოლია
\(F\)ლ\(=qvB\sin \alpha\).
ამ ძალას ლორენცის ძალას უწიდებენ. ამ გამოსახულებაში \(\alpha\) კუთხე \(\vec{v}\) სიჩქარესა და \(\vec{B}\) მაგნიტული ინდუქციის ვექტორს შორის კუთხის ტოლია. დადებითად დამუხტულ ნაწილაკზე მომქმედი ლორენცის ძალის მიმართულება, ამპერის ძალის მიმართულების მსგავსად შეიძლება მარცხენა ხელის ან ბურღის წესის საშუალებით დადგინდეს. \(\vec{F}\)ლ, \(\vec{B}\) და \(\vec{v}\) ვექრორების ურთიერთ განლაგება დადებითად დამუხტული ნაწილაკისთვის ნახ. 1-ზეა ნაჩვენები.
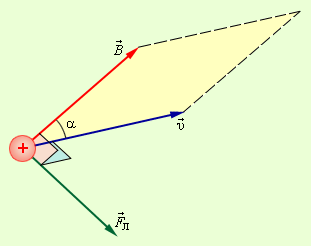
ნახ. 1.
\(\vec{F}\)ლ, \(\vec{B}\) და \(\vec{v}\) ვექრორების ურთიერთ განლაგება. ლორენცის \(\vec{F}\)ლ ძალა რიცხობრივად \(\vec{v}\) და \(\vec{B}\) ვექტორებზე აგებული პარალელოგრამის ფართობის q მუხტზე ნამრავლის ტოლია
ლორენცის ძალა \(\vec{v}\) და \(\vec{B}\) ვექტორების მართობულია. დამუხტული ნაწილაკის მაგნიტურ ველში მოძრაობისას ლორენცის ძალა მუშაობას არ ასრულებს. ამიტომ ნაწილაკის მოძრაობისას ნაწილაკის სიჩქარის სიდიდე არ იცვლება.
თუ დამუხტული ნაწილაკი ლორემცის ძალის მოქმედებით ერთგვაროვან მაგნიტურ ველში მოძრაობს, ხოლო მისი \(\vec{v}\) სიჩქარე \(\vec{B}\) ვექტორის მართობულ სიბრტყეში მდებარეობს, მაშინ ნაწილაკები იმოძრავებენ წრეწირზე, რომლის რადიუსია
\(R=\frac{mv}{qB}\)
ამ შემთხვევაში ლორენცის ძალა ცენტრისკენული ძალის როლს ასრულებს (ნახ. 2).
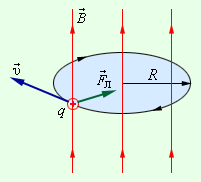
ნახ. 2.
დამუხტული ნაწილაკის წრიული მოძრაობა ერთგავროვან მაგნიტურ ველში
ერთგავროვან მაგნიტურ ველში ნაწილაკის ბრუნვის პერიოდი ტოლია
\(T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\).
ეს გამოსახულება უჩვენებს, რომ მოცემული მასის დამუხტული ნაწილაკების ბრუნვის პერიოდე არ არის დამოკიდრბული \(v\) სიჩქარესა და ტრაექტორიის R რადიუსზე.
წრიულ ტრაექტორიაზე დამუხტული ნაწილაკების მოძრაობის კუთხურ სიჩქარეს
\(\omega =\frac{v}{R}=v\frac{qB}{mv}=\frac{qB}{m}\)
ციკლოტრონულ სიჩქარეს უწოდებენ. ციკლოტრონული სიჩქარე არ არის დამოკიდებული ნაწილაკის სიჩქარეზე (და ე.ი. არც კინეტიკურ ენერგიაზე). ეს გარემოება გამოიყენება ციკლოტრონებში - მძიმე ნაწილაკების ( პროტონების, იონების) ამაჩქარებლებში. ციკლოტრონის პრინციპული სქემა ნახ. 3-ზეა მოყვანილი.

ნახ. 3.
გამუხტული ნაწილაკის მოძრაობა ციკლოტრონის ვაკუუმურ კამერაში
ძლიერი ელექტრომაგნიტის პოლუსებს შორის ვაკუუმური კამერა თავსდება, რომელშიც ორი ღრუ ნახევარცილინდრის ფორმის მეტალური ელექტროდია მოთავსებული (დუანტები). დუანტებზე ცვალდი ელექტრული ძაბვაა მოდებული, რომლის სიხშირეც ციკლოტრონული სიხშირის ტოლია. დამუხტული ნაწილაკები შეჰყავთ ვაკუუმური კამერის ცენტრში. ნაწილაკები დუანტებსშორისი ელექტრული ველის მოქმედებით აჩქარდებიან. დუანტებს შიგნით ნაწილაკები ლორენცის ძალის მოქმედებით ნახევარ წრეებზე მოძრაობენ, რომელთა რადიუსები ნაწილაკების ენერგიის ზრდასთან ერთად იზრდებია. ყოველთვის, როცა ნაწილაკი ჩაიფრენს დუანტებს შორის ნაპრალში (ღრეჭოში) ის ელექტრული ველის გავლენით ჩქარდება. ამგვარად, ციკლოტრონში, ისევე როგორც ყველა სხვა ამაჩქარებელში, დამუხტული ნაწილაკი ელექტრული ველის მოქმედებით ჩქარდება, ხოლო ტრაექტორიაზე მაგნიტური ველის გავლენით კავდება. ციკლოტრონები პროტონების 20 მეგავოლტამდე აჩქარების საშუალებას იძლევიან.
ერთგვაროვანი მაგნიტური ველი მრავალ ხელსაწყოში და, კერძოდ, მას-სპექტრომეტრებში გამოიყენება. მას-სპექტრომეტრები ხელსაწყოებია, რომელთა საშუალებით დამუტული ნაწილაკების - იონებისან სხვადასხვა ნივთიერების ატომის ბირთვების - მასის გაზომვაა შესაძლებელი. მას-სპექტრომეტრების გამოიყენება იზოტოპების, ე.ი.ერთნაერი მუხტის, მაგრამ სხვადსხვა მასის ატომების (მაგალითად,20Ne და 22Ne) გასაყოფად. უმარტივესი მას-სპექტრომეტრი ნახ. 4-ზეა ნაჩვენები. S წყაროდან გამოფრენილი იონები, რამოდენიმე პატარა ხვრელში შედიან და ქმნიან ვიწრო ნაკადს. შემდეგ ისინი სიჩქარეების სელექტორში ხვდებიან, რომელშიც ნაწილაკები მოძრაობენ ურთიერთგადამკვეთ ელექტრულ და მაგნიტურ ველებში. ელექტრული ველი ბრტყელი კონდენსატორის ფირფიტებს შორის იქმნება, მაგნიტური ველი კი, ელექტრომაგნიტის პოლუსებს შორის ღრეჭოში. დამუხტული ნაწილაკის საწყისი \(\vec{v}\) სიჩქარე \(\vec{E}\) და \(\vec{B}\) ვექტორების მართობულია. ურთიერთგადამკვეთ ელექტრულ და მაგნიტურ ველებში მოძრავ ნაწილაკზე მოქმედებს ელექტრული ძალა \(q\vec{E}\) და ლორენცის მაგნიტური ძალა. თუ \(E=vB\) ეს ძალები ზუსტად აწონასწორებენ ერთმანეთს. თუ ეს პირობა სრულდება, ნაწილაკი თანაბრად და წრფივად იმოძრავებს და, გაიფრენს რა კონდენსატორში, გაივლის ეკრანის ხვრელში. ელექტრული და მაგნიტური ველების გარკვეული მნიშვნელობებისათვის სელექტორი \(v=\frac{E}{B}\) სიჩქარით მოძრავ ნაწილაკებს გამოჰყოფს.
ამის შემდეგ ერთნაერი სიჩქარეების მქონე ნაწილაკები ხვდებიან მას-სპექტრომეტრის კამერაში, სადაც შექმნილია ერთგვაროვანი \(\vec{B}'\) მაგნიტური ველი. კამერაში ნაწილაკები, ლორენცის ძალის მოქმედებით, მაგნიტური ველის მართობულ სიბრტყეში მოძრობენ. ნაწილაკების ტრაექტორიები \(R=\frac{mv}{q{B}'}\)წრეწორებს წარმოადგენენ. ცნობილი \(v\) და B' სიდიდეების შემთხვევაში ტრაექტორიის რადიუსების გაზომვით შეიძლება q / m ფარდობის განსაზრვრა. იზოტოპების შემთხვევაში (q1 = q2) მას-სპექტრომეტრი სხვადასხვა მასების მქონე მაწოლაკების გაყოფის საშუალებას იძლევა.
თანამედროვე მას-სპექტრომეტრები საშუალებას იძლევიან დამუხტული ნაწილაკის მასა გაიზომის 10–4-ზე მეტი სიზუსტით.

ნახ. 4.
სიჩქარეების სელექტორი და მას-სპექტრომეტრი
თუ ნაწილაკის \(\vec{v}\) სიჩქარეს აქვს \(\vec{v}_{\parallel}\) მაგნიტური ველის გასწვრივი მდგენელი, მაშინ ასეთი ნაწილაკი ერთგვაროვან მაგნიტურ ველში სპირალზე იმოძრავებს. ამ დროს სპირალის R რადიუსი დამოკიდებულია \(\vec{v}\) ვექტორის მაგნიტური ველის მართობული \(v_{\perp }\) მდგენელის სიდიდეზე, ხოლო სპირალის ბიჯი p - გასწვრივი \(v_{\parallel}\) მდგენელის სიდიდიზე (ნახ. 5).

ნახ. 5.
დამუხტული ნაწილაკის მოძრაობა ერთგვაროვან სპირალურ მეგნიტირ ველში
ამგვარად, დამუხტული ნაწილაკის ტრაექტორია თითქოს მაგნიტური ინდუქციის წირს ემთხვევა. ეს მოვლენა ტექნიკაში გამოიყენება მაღალტემპერატურული პლაზმის -ანუ 106 K რიგის ტემპერატურაზე მთლიანად იონიზირებული გაზის - მაგნიტური იზოლაციის მიზნით. ნივთიერება ასეთ მდგომარეობაში მიიღება „ტოკომაკის“ ტიპის დანადგარებში თერმობირთვული რეაქციების შესწავლის დროს. პლაზმა არ უნდა ეხებოდეს კამერის კედლებს. თერმოიზოლაცია მიიღწევა სპეციალური კონფიგურაციის მაგნიტური ველის შექმნით. მაგალითისათვის ნახ. 6-ზე გამოსახულია დამუხტული ნაწილაკის მოძრაობა მაგნიტურ „ბოთლში“ (ან სათაგურში).
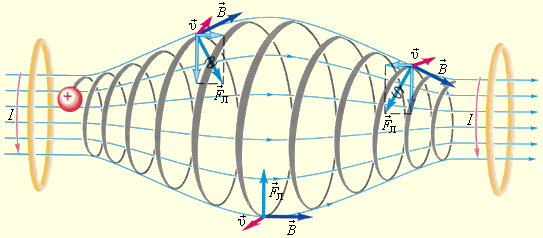
ნახ. 6.
მაგნიტური „ბოთლი“. დამუხტული ნაწილაკები „ბოთლის“ საზღვრებიდან არ გამოდიან. „ბოთლის“ მაგნიტური ველი შეიძლება ორი მრგვალი დენიანი კოჭას საშუალებით შეიქმნას
ანალოგიური მოვლენა ხდება დედამიწის მაგნიტურ ველში, რომელიც ყოველივე ცოცხალის დამცველია კოსმოსური სივრციდან მომავალი დამუხტული ნაწილაკების ნაკადებისაგან. დედამიწის მაგნიტური ველი „ჩაიჭერს“ კოსმოსიდან (ძირითადად მზიდან) მომავალ სწრაფ დამუხტილ ნაწილაკებს და ქმნის ე.წ. რადაიციულ სარტყელს (ნახ. 7), რომელშიც ნაწილაკი, როგორც მაგნიტურ სათაგურში აქეთ-იქით მოძრაობს სპირალის მსგავს ტრაექტორიებზე ჩრდილოეთ და სამხრეთ პოლუსებს შორის წამის ნაწილების რიგის დროის პერიდით. მხოლიდ პოლარულ არეებში ნაწილაკების რაღაც ნაწილი აღწევს ატმოსფეროს ზედა ფენაბში და ჩრდილოეთის ციალს იწვევს. დედამიწის რადიაციული სარტყელი 500კმ-დან ათობით დედამიწის რადიუსამდე მანძილზე ვრცელდება. უნდა გვახსოვდეს, რომ დედამიწის სამხრეთ მაგნიტური პოლუსი მდებარეობს ჩრდილოეთ გეოგრაფიული პოლუსის მახლობლად (გრენლანდიის ჩრდილო დასავლეთით). დედამიწის მაგნეტიზმის ბუნება ჯერკიდევ არ არის შესწავლილი.

ნახ. 7.
დედამიწის რადიაციული სარტყელი. მზიდან მომავალი სწრაფი დამუხტული ნაწილაკები (ძირითადად ელექტრონები და პროტონები) რადიაციული სარტყლის მაგნიტურ სათაგურში ხვდებიან. ნაწილაკებს შეუძლიათ დატოვონ სარტყელი პოლუსების არეებში და შეიჭრნენ ზედა ატმოსფერულ ფენებში და ჩრდილოეთის ციალი გამოიწვიონ
{loadnavigation}
სხვადასხვა კონფიგურაციის მუდმივი დენის მაგნიტული ველები ექსპერიმენტულად ფრანგმა მეცნიერებმა ჟ.ბიომ და ფ.სავარმა ()1820 წ.) შეისწავლეს. ისინი მივიდნენ დასკვნამდე, რომ სადენებში გამავალი დენების მაგნიტური ველის ინდუქცია განისაზღვრება გამტარების ყველა ცალკეული უბნის საერთო მოქმედებით. მაგნიტური ველი სუპერპოზიციის პრინციპს ექვემდებარება:
თუ მაგნიტური ველი რამოდენიმე დენიანი სადენისგანაა შექმნილი, ტოლქმედი ველის ინდუქცია ცალცალკეული გამტარის მიერ შექმნილი ველების ინდუქციების ჯამის ტოლია.
დენიანი გამტარის \(\vec{B}\) ინდუქცია შეიძლება წარმოდეგნილი იქნეს გამტარის ცალცალკეული უბნების მიერ შექმნილი ელემენტარული \(\Delta \vec{B}\) ინდუქციების ვექტორული ჯამის სახით. ცდისას შეუძლებელია დენიანი გამტარის ცალკეული უბნების გამოყოფა, რადგან მუდმივი დენი ყოველთვის ჩაკეტილია. შეიძლება გაიზომოს მხოლოდ ჯამური ინდუქცია მაგნიტური ველისა, რომელსაც დენის ყველა ელემენტი ქმნის. ბიო-სავარის კანონი განსაზღვრავს I სიგრძის დენიანი გამტარის მცირე Δl სიგრძის უბნის მიერ შექმნილ მაგნიტურ \(\Delta \vec{B}\) ინდუქციის წვლილს ჯამური მაგნიტური ველის \(\vec{B}\) ინდუქციაში.
\(\Delta \vec{B}=\frac{\mu _{0}I\Delta l\sin \alpha }{4\pi r^{2}}\)
აქ r – მოცემული Δl უბნიდან დაკვირვების წერტილამდე მანძილია, α –დაკვირვების წერტილისკენ მიმართულებასა და მოცემულ უბანში დენის მიმართულებას შორი კუთხეა, μ0 – მაგნიტური მუდმივაა. \(\Delta \vec{B}\) ვექტორის მიმართულება ბურღის წესით განისაზღვრება: იგი ემთხვევა ბურღის სახელურის ბრუნვის მიმართულებას , როცა ბურღვის მიმართულება ემთხვევა დენის მიმართულებას. ნახ. 1 იძლევა ბიო-სავარის კანონის ილუსტრაციას წრფივი დენიანი გამტარის მაგნიტური ველის მაგალითზე. თუ მაგნიტურ ველში წრფივი დენიანი გამტარის ყველა ცალკეული უბნის წვლილის აჯამვას (ინტეგრირებას) მოვახდენთ, წრფივი დენის მაგნიტური ინდუქციისთვის მივიღებთ ფორმულას:
\(B=\frac{\mu _{0}}{2\pi }\frac{I}{R}\).
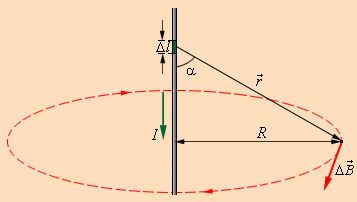
ნახ. 1.
ბიო-სავარას კანონის ილუსტრაცია
ბიო-სავარის კანონი სხვადსხვა კონფიგურაციის დენების მაგნიტური ველების გათვლის საშუალებას იძლევა. მაგალითად, ძნელი არ არის წრიული დენის ცენტრში მაგნირური ველის გამოთვლა. ამ გამოთვლებს მივყავართ ფორმულამდე
\(B=\frac{\mu _{0}}{2 }\frac{I}{R}\)
სადაც R – წრიული გამტარის რადიუსია. \(\vec{B}\) ვექტორის მიმართულების განსაზღვრისთვის ბურღის წესის გამოყენებაა შესაძლებელი, ოღონდ ახლა სახელური უნდა ვაბრუნოთ წრიული დენის მიმართულებით, ხოლო ბურღვის მიმართულება მაგნიტური ველის ინდუქციის ვექტორის მიმართულებას ემთხვევა.
მაგნიტური ველის გათვლები ხშირად მაგნიტური ველის შემქმნელი დენის კონფიგურაციის სიმეტრიის გათვალისწინებით მარტივდება. ამ შემთხვევაში შეიძლება მაგნიტური ინდუქციის ვექტორის ცირკულაციის თეორიის გამოყენება, რომელიც დენების მაგნიტური ველის თეორიაში იგივე როლს ასრულებს, რასაც გაუსის თეორემა ელექტროსტატიკაში.
ავხსნათ \(\vec{B}\) ვექტორის ცირკულაციის ცნება. ვთქვათ სივრცეში, სადაც მაგნიტური ველია შექმნილი, არჩეულია რაღაც პირობითი ჩაკეტილი კონტური (არა აუცილებლად ბრტყელი) და მითითებულია მისი შემოვლის დადებითი მიმართულება. ყოველ ცალკეულ მცირე Δl უბანზე შეიძლება განისაზრვროს მოცემული უბნის \(\vec{B}\) ვექტორის მხებზე \(B_{l}\) მდგენელი, ე.ი. განისაზღვროს კონტურის მოცემულ უბანში მხების მიმართულებაზე \(\vec{B}\) ვექტორის პროექცია (ნახ. 2).

ნახ. 2.
წინასწარ მითითებული შემოვლის მიმართულების მქონე ჩაკეტილი (L) კონტური. გამოსახულია მაგნიტური ველის წარმომქმნელი I1, I2 და I3 დენები
\(\vec{B}\) ვექტორის ცირკულაციას უწოდებენ მთელ L კონტურზე აღებული \(B_{l}\Delta l\) ნამრავლების ჯამს:
ცირკულაცია ვექტორისა \(\vec{B}=\sum_{\left ( L \right )}B_{l}\Delta l\)
მაგნიტური ველის შემქმნელი ზოგი დენი შეიძლება მსჭვალავდეს L კონტურს, მაშინ როცა სხვები კონტურს მიღმა რჩებოდნენ.
ცირკულაციის თეორამა ამტკიცებს, რომ მუდმივი დენების მაგნიტური ველის \(\vec{B}\) ვექტორის ნებისმიერ L კონტურზე ცირკულაცია ყოველთვის მაგნიტური მუდმივის კონტურის განმსჭვალავ ყველა დენის ჯამზე ნამრავლის ტოლია:
\(\sum_{\left ( L \right )}B_{l}\Delta l=\mu _{0}\sum I_{i}\)
მაგალითის სახით ნახ. 2-ზე რამდენიმე მაგნიტური ველის შემქმნელი დენიანი გამტარია გამოსახული. I2 და I3 დენები L კონტურს მსჭვალავენ ურთიერთსაწინააღმდეგო მიმართულებით. მათ სხვდასხვა ნიშანი უნდა მიეწეროს - დადებითად უნდა ჩაითვალის დენები, რომლებიც კუნტურის შემოვლის მარჯვენა ბურღის წესთან არიან დაკავშირებული. ესე იგი , I3 > 0, ხოლო I2 < 0. I1 დენი კონტურს არ მსჭვალავს.
ამ მაგალითისთვის ცირკულაციის თეორემას აქვს სახე:
\(\sum_{\left ( L \right )}B_{l}\Delta l=\mu _{0}\left ( I_{3}-I_{2} \right )\)
ზოგადი სახით ცირკულაციის თეორემა ბიო-სავარას კანონიდან და სუპერპუზიციის პრინციპიდან გამოდის.
ცირკულაციის თეორემის გამოყენების უბრალო მაგალითს წარმოსდგენს წრფივი დენიანი გამტარის ველის მაგნიტური ინდუქციის ფორმულის გამოყვანა. მოცემული ამოცანის სიმეტრიის გათვალიწინებით, მიზანშეწონილია R რადიუსიანი წრიული L კონტურის არჩევა, რომელიც გამტარის მართობულ სიბრტყეში მდებარეობს. სიმეტრიიდან გამომდინარე \(\vec{B}\) ვექტორი მიმართულია \(\left (B_{l}=B \right )\) მხების გასწვრივ, ხოლო მისი სიდიდე ერთნაირია წრეწირის ყველა წერტილში. ცირულაციის თეორემის გამოყენება იძლევა ტოლობას:
\(\sum_{\left ( L \right )}B_{l}\Delta l=2\pi RB=\mu _{0}I\)
აქედან გამოდის ადრე მოყვანილი წრფივი დენიანი გამტარის ველის მაგნიტური ინდუქციის სიდიდის ფორმულა.
ეს მაგალით უჩვენებს, რომ თეორემა მაგნიტური ველი \(\vec{B}\) ინდუქციის ცირკულაციის შესახებ შეიძლება გამოყენებული იქნეს ისეთი მაგნიტური ველების გათვლისთვის, რომლებიც დენების სიმეტრიული განაწილებით იქმნება, როცა სიმეტრიის მოსაზრებებიდან გამომდინარე შეიძლება „გამოვიცნოთ“ ველის საერთო სრუქტურა.
პრაქტიკაში არსებობს ცირკულაციის თეორიით მაგნიტური ველების გათვლის არა ერთი მაგალითი. ერთი ასეთი მაგალითია ტოროიდული კოჭას ველის გამოთვლის ამოცანა. (ნახ. 3).
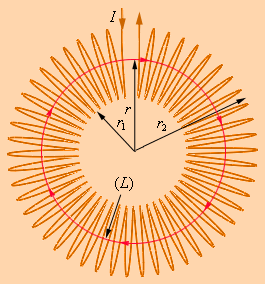
ნახ. 3.
ტოროიდულ კოჭასათვის ცირკულაციის თეორემის გამოყენების მაგალით
იგულისხმება, რომ კოჭა მჭიდროდ. ე.ი. ხვიახვიაზეა დახვეული არამაგნიტურ ტოროიდულ გულზე. ასეთ კოჭაში მაგნიტური ინდუქციის წირები კუჭას შიგნით არიან ჩაკეტილი და კონცენტრულ წრეწირებს წარმოადგენენ. ისინი ისე არიან მიმართული, რომ მათ გასწვრივ ყურების შემთხვევაში, ჩვენ ხვეულებში უნდა დავინახოთ დენი, რომელიც საათის ისრის მიმართულების ცირკულირებს. იგი ნახ. 3-ზე გამოსახულია ერთერთი r1 ≤ r < r2 რადიუსიანი წირის სახით. მივუყენოთ ცირკულაციის თეორემა L წრიულ კონტურს, რომელიც ნახ. 3-ზე გამოსახულ მაგნიტული ველის ინდუქციის წირს ემთხვევა. სიმეტრიის მოსაზრებებიდან გამომდინარე ნათელია, რომ \(\vec{B}\) ვექტორის სიდიდე მთელი ამ წირის გასწვრივ ერთნაერია. ცირკულაციის თეორემის მიხედვით შეიძლება ჩავწეროთ:
B ∙ 2πr = μ0IN,
სადაც N – ხვეულების სრული რიცხვი, ხოლო I – კოჭას ხვეულებში გამავალი დენია. აქედან გამომდინარე,
\(B=\frac{\mu \mu _{0}IN}{2\pi r}\)
ამგვარად, მაგნიტური ინდუქციის ვექტორის სიდიდე ტოროიდულ კოჭაში r რადიუსზეა დამოკიდებული. თუ კოჭას გული თხელია, ე.ი. r2 – r1 << r, მაშინ კოჭას შიგნით მაგნიტური ველი პრაქტიკულად ერთგვაროვანია. სიდიდე n = N / 2πr კოჭას სირძის ერთეულძე ხვიათა რიცხვს წარმოადგენს. ასეთ შმთხვევაში
B = μ 0I n.
ამ გამოსახულებაში ტორის რადიუსი არ შედის, ამიტომ იგი ზღვრულ r → ∞ შემთხვევაშიც სამართლიანია. მაგრამ ზღვარში ტოროიდული კოჭას ყოველი ნაწილი შეიძლება განვიხილოთ, როგორც გრძელი წრფივი კოჭა. ასეთ კოჭებს სოლეიდონებს უწოდებენ. სოლეიდონის ბოლოებიდან დაშორებით მაგნიტური ინდუქციის სიდიდე ტოროიდული კოჭას მსგავსი ფორმულით გამოისახება.
ნახ. 4-ზე სასრული სიგრძის კოჭას მაგნიტური ველია გამოსახილი. ყურადღება უნდა მიექცეს იმას, რომ კოჭას ცენტრალურ ნაწილში მაგნიტური ველი პრაქტიკულად ერთგვაოვანია და გაცილებით ძლიერია ვიდრე კოჭას გარეთ. ამაზე მაგნიტული ინდუქციის წირების სიხშირე მიუთითებს. უსასრულოდ გრძელი სოლეიდონის ზღვრულ შემთხვევაში ერთგვაროვანი მაგნიტური ველი მთლიანად მასშია თავმოყრილი.
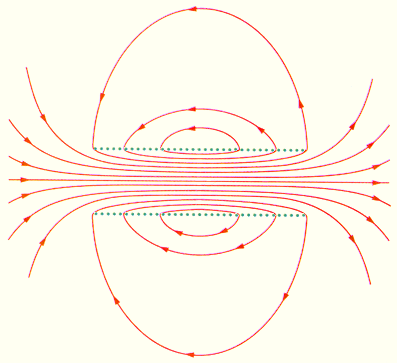
ნახ. 4.
სასრული სიგრძის კოჭას მაგნიტური ველი. სოლეიდონის ცენტრში მაგნიტური ველი პრაქტიკულად ერთგვაროვანია და სიდიდი მნიშვნელოვნად აჭარბებს კოჭას გარე ველს
უსასრულიდ გრძელი სოლეიდონის შემთხვევაში გამოსახულება მაგნიტური ველის ინდექციისთვის შეიძლება მივიღოთ უშუალოდ ნახ. 5-ზე ნაჩვენები მართხკუთხა კონტურისათვის ცირკულაციის თეორემის გამოყენებით.

ნახ. 5.
ცირკულაციის თეორიის გამოყენება უსასრულოდ გრძელი სოლეიდონის მაგნიტური გათვლისთვის
მაგნიტური ინდუქციის ვექტორს ნულისაგან განსხვავებული გეგმილი აქვს abcd კონტურის მხოლოდ ab გვერდზე. აქედან გამომდინარე, \(\vec{B}\) ვექტორის კონტურის ირგვლივ ცირკულაცია \(Bl\) -ის ტოლია, სადაც \(l\) - ab გვერდის სიგრძეა. სოლეინოიდის ხვიათა რიცხვი, რომლებიც abcd კონტურს მსჭვალევენ, ტოლია \(n-l\), სადაც n – სოლეიდონის სიგრძის ერთეულზე ხვიათა რიცხვია, ხოლო კონტურის გამსჭვალევი სრული დენი ტოლია \(Inl\) . ცირკულაციის თეორიის თანახმად,
\(Bl=\mu _{0}Inl\),
აქედან
\(B=\mu _{0}In\)
ეს გამოსახულება ადრე მიღებულ თხელი ტოროიდული კოჭას მაგნიტური ველის ფორმულას ემთხვევა.
{loadnavigation}
მანიტური მოვლებები ჯერ კიდევ ძველ სამყაროში იყო ცნობილი. კომპასი 4500 წლის წინ იქნა გამოგონებული. ევროპაში ის დაახლოებით ახალი წელთაღრიცხვის XII საუკუნაში გამოჩნდა. მაგრამ მხოლოდ XIX საუკუნეში დადგინდა კავშირი ელექტრობასა და მაგნიტიზმს შორი და შეიქმნა წარმოდგენა მაგნიტუ ველზე.
პირველი ექსპერიმენტები (1820 წ.) რომლებმაც აჩვენეს, რომ ელექტრულ და მაგნიტურ მოვლენებს შორის ღრმა კავშირია, დანიელ ფიზიკოსს ჰ.ერსტედს ეკუთვნის. ამ ცდებმა აჩვენეს, რომ დენიანი გამტარის ახლოს მოთავსებულ მაგნიტურ ისარზე მოქმედებს ძალები, რომლებიც მის შემობრუნებას ცდილობენ. ამავე წელს ფრანგი ფიზიკოსი ა.ამპერი დააკვირდა ორი დენიანი გამტარის ერთმანეთზე ძალით ურთიერთქმედებას და დაადგინა დენების ურთიერთქმედების კანონი.
თანამედროვე წარმოდგენების მიხევით, დენიანი გამტარები ერთმანეთზე ძალებით ურთიერთქმედებენ არა უშუალოდ, არამედ მათი გარემომცველი მაგnიტური ველის საშუალებით.
მაგნიტური ველის წყაროებს მოძრავი ელექტრული მუხტები (დენები) წარმოადგენენ. მაგვიტური ველი დენიანი გამტარის გარემომცველ სივრცეში აღიძვრება, ისევე როგორც უძრავი ელექტრული მუხტის გარშემო ელექტრული ველი აღიძვრება. მუდმივი მაგნიტების მაგნიტური ველი ასევე ელექტრული მიკროდენებით აღიძვრება, რომლებიც ნივთიერების მოლეკულის შიგნით ცირკულირებენ (ამპერის ჰიპოთეზა).
XIX საუკუნის მეცნიერები ცდილობდნენ მაგნიტური ველის თეორიის შექმნას ელექტრულის მსგავსად და უშვებდნენ ე.წ. ორი სხვადასხვა ნიშნის (მაგალითდ, მაგნიტური ისრის N ჩრდილოეთ და S სამხრეთ პოლუსები) მაგნიტური მუხტების არსებობას. მაგრამ ცდებმა აჩვენეს, რომ იზოლირებული მაგნიტური მუხტები არ არსებობენ.
დენების მაგნიტური ველი პრინციპულად განვსხვავდება ელექტრული ველისგან. მაგნიტური ველი, ელექტრულისგან განსხვავებით, ძალით მოქმედებს მხოლოდ მოძრავ მუხტებძე (დენებზე).
მაგნიტური ველის ასაღწერად აუცილებელია, ელექტრული ველის დაძაბულობის \(\vec{E}\) ვექტრორის მსგავსად, ველის ძალური მახასიათებლის შემოტანა. ასეთ მახასიათებელს მაგნიტური ინდუქციის \(\vec{B}\) ვექტორი წარმოადგენს, რომელიც მაგნიტუ ველში დენებზე ან მოძრავ მუხტზე მომქმედ ძალას განსაზღვრავს.
\(\vec{B}\) ვექტორის დადებით მიმართულებად, მაგნიტურ ველში თავისუფლად მბრუნავი, მაგნიტური ისრის S სამხრეთ პოლუსიდან N ჩრდილოეთ პოლუსისაკენ მიმართულებაა მიღებული. ამგვარად, დენის მიერ ან მუდმივი მაგნიტით შექმნილი მაგნიტული ველის პატარა მაგნიტური ისრით გამოკვლევისას, შეიძლება \(\vec{B}\) ვექტორის ორიენტაცია სივრცის ყოველ წერტილში განისაზღვროს. ასეთი გამოკვლევები მაგნიტური ველის სივრცული სტრუქტურის თვალნათლივ წარმოდგენის საშუალებას იძლევიან. ელექტროსტატიკაში ძალხაზების ანალოგიურად შეიძლება აიგოს მაგნიტური ინდუქციის წირები, რომელთა ყოველ წერტილში \(\vec{B}\) ვექტორი მხების გასწვრივაა მიმართული. მუდმივი მაგნიტისა და დენიანი კოჭას ველის მაგნიტური ინდუქციის წირების მაგალითები ნახ. 1-ზეა მოყვანილი.
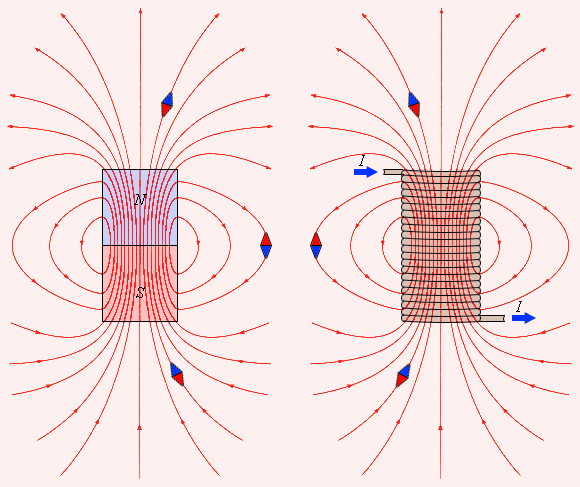
ნახ. 1.
მუდმივი მაგნიტისა და დენიანი კოჭას ველის მაგნიტური ინდუქციის ხაზები. საცდელი მაგნიტური ისრები ინდუქციის წირების მხების გასწვრივაა ორიენტირებული
ყურადღება მიაქციეთ მუდმივი მაგნიტისა და დენიანი კოჭას მაგნიტური ველის ანალოგიურობას. მაგნიტური ინდუქციის ხაზები ყოველთვის ჩაკეტილია, ისინი არსად არ წყდებიან. ეს ნიშნავს, რომ მაგნიტურ ველს მაგნიტური მუხტის წყარი არ გააჩნია. ასეთ თვისების მქონე ძალურ ველებს, გრიგალურს უწოდებენ. მაგნიტული ინდუქციის სურათს შეიძლება დავაკვირდეთ წვრილი მაგნიტური ნაქლიბის საშუალებით, რომელიც მაგნიტურ ველში მაგნიტდება და პატარა მაგნიტური ისრებია მსგავსად, ინდუქციის წირების გასწვრივ ლაგდებიან.
მაგნიტური ველი რაოდენობრივი აღწერისათვის მითითებული უნდა იყოს არამარტო \(\vec{B}\) ვექტორის მიმართულების განსაზღვრის მეთოდი, არამედ მისი მოდული. ამის გაკეთება ყველაზე იოლია, თუ გამოსაკვლევ მაგნიტურ ველში დენიან გამტარს შევიტანთ და ამ გამტარის ცალკეულ სწორხაზოვან მონაკვეთზე მომქმედ ძალას გავზომავთ. გამტარის ამ მონაკვეთს არაერთგვაროვანი მაგნიტური ველის არეებთან ზომებთან შედარებით საკმარისად მცირე Δl სიგრძე უნდა ჰქონდეს. როგორც ამპერის ცდებმა უჩვენეს, გამტარის მონაკვეთზე მომქმედი ძალა დენის ძალის, ამ მონაკვეთის სიგრძისა და მაგნირური ინდუქციის ვექტორისა და დენის მიმართულებებს შორის კუთხის სინუსის პროპორციულია:
F ~ IΔl sin α.
ამ ძალას ამპერის ძალა ეწოდება. ის მოდულით მაქსიმალურ Fmax მნიშვნელობას აღწევს, როცა დენიანი გამტარი მაგნირური ინდუქციის წირების მართობულადაა ორიენტირებული. \(\vec{B}\) ვექტორის მოდული შემდეგნაირად ისაზღვრება:
მაგნირური ინდუქციის ვექტორის მოდული ტოლია სწორ გამტარზე მომქმედი ამპერის ძალის მაქსიმალური მნიშვნელობის ფარდობისა დენის I ძალისა და მისი Δl სიგრძის ნამრავლზე:
\(B=\frac{F_{max}}{I\Delta l}\).
ზოგად შემთხვევაში ამპერის ძალა გამოისახება ფორმულით:
\(F=IB\Delta l\sin\alpha\)
ამ ფორმულას ამპერის კანონს უწოდებენ.
სი ერთეულთა სისტემაში მაგნიტური ინდუქციის ვექტორის ერთეული ისეთ მაგნირური ველის ინდუქციაა, რომელშიც 1 ა დენის ძალის შემთხვევაში გამტარის ყოველ მეტრზე მოქმედებს 1 ნ მაქსიმალური ამპერის ძალა მოქმედებს. ამ ერთეულს ტესლას (ტეს) უწოდებენ.
1ტეს=1ნ/(ა*მ)
ტესლა ძალიან დიდ ერთეულია. დედამიწის მაგნიტური ველი დაახლოებით 0,5·10–4 ტეს. დიდი ლაბორატორიული ელექტრომაგნიტის მიერ შექმნილი ველი 5 ტესლა.
ამპერის ძალა მაგნიტური ინდუქციის \(\vec{B}\) ვექტორისა და გამტარში გამავალი დენის მიმართულების მართობულადაა მიმართული. ამპერის ძალის მიმართულების განსაზღვრისათვის ჩვეულებრივ მარცხენა ხელის წესი გამოიყენება: თუ მარცხენა ხელს ისე მივმართავთ, რომ \(\vec{B}\) ინდუქციის წირები ხელიგულში შედის, ხოლო გაჭიმული თითები დენის გასწვრივაა, მაშინ გაშლილი ცერა თითი გამტარზე მომქმედი ძალის მიმართულებას უჩვენებს (ნახ. 2).

ნახ. 2.
მარცხენა ხელის წესი და ბურღის წესი
თუ კუთხე მაგნირური ინდუქციის \(\vec{B}\) ვექტორისა და გამტარში დენის მიმართულებას შორის 90°-საგან განსხვავებულია, მაშინ ამპერის \(\vec{F}\) ძალის მიმართულების განსაზღვრისათვის უფრო მოსახერხებელია ბურღის წესი: წარმოსახვითი ბურღი უნდა განლაგდეს \(\vec{B}\) ვექტორისა და გამტარის შემცველი სიბრტყის მართობულად, შემდეგ ბურღი უნდა მობრუნდეს დენის მიმართულებიდან \(\vec{B}\) ვექტორის მიმართულებისკენ. ბურღის წვეროს გადაადგილების მიმართულება არის ამპერის \(\vec{F}\) ძალის მიმართულება (ნახ. 2).
მაგნიტური ურთიერთქმედების მნიშვნელოვან მაგალითს პარალელური დენების ურთიერთქმედება წარმოადგენს. ამ მოვლენის კანონზომიერება ექსპერიმენტულად ამპერმა დაადგინა. თუ ორ პარალელურ გამტარში ელექტრული დენი გადის ერთიდაიგივე მიმართულებით. მაშინ ადგილი აქვს გამტარების ურთიერთმიზიდვას. თუ დენები ურთიერთსაწინააღმდეგოდ მიედინება, გამტარები განიზიდებიან.
დენების ურთიერთქმედება გამოწვეულია მაგნიტური ველებით: ერთი დენის მაგნიტური ველი ამპერის ძალით მოქმედებს მეორეზე და პირიქით.
ცდები უჩვენებენ. რომ თითოეული გამტარის Δl სიგრძის მონაკვეთზე მომქმედი ძალის მოდული დენის I1 და I2 ძალების და მონაკვეთის Δl სიგრძის პირდაპირპროპორციულია და მათ შორის R მანძილის უკუპროპორციული:
\(F=k\frac{I_{1}I_{2}\Delta l}{R}\),
საერთაშორისო სი სისტემაში პროპორციულობის k კოეფიციენტი ჩაიწერება შემდეგი სახით:
k = μ0 / 2π,
სადაც μ0 – მუდმოვი სიდიდეა, რომელსაც მაგნიტური მუდმივა ეწოდება. მაგნიტური მუდმივის შემოტანა სი სისტემაში მრავალ ფორმულას ამარტივებს. მისი რიცხვითი მნიშვნელობა ტოლია
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2,
პარალელური დენების მაგნიტური ურთიურთქმედების კანონის გამომსახველ ფორმულას აქვს სახე:
\(F=\frac{\mu _{0}}{2\pi }\frac{I_{1}I_{2}\Delta l}{R}\), აქედან არაა ძნელი თითოეული სწორი სადენის მაგნიტური ველის ინდუქციის გამოსახულების მიღება. სწორი დენიანი სადენის მაგნიტურ ველს უნდა ჰქონდეს ღერძული სიმეტრია და, აქედან გამომდინარე, მაგნიტური ინდუქციის ჩაკეტილი წირები შეიძლება იყვნენ მხოლოდ გამტარის მართობულ სიბრტყეში განლაგებული კონცენტრული წრეები. ეს ნიშნავს, რომ პარალელური I1 და I2 დენების მაგნიტური ინდუქციის \(\vec{B}_{1}\) და \(\vec{B}_{2}\) ვექტორები ორივე დენის მართობულ სიბრტყეში მდებარეობენ. ამიტომ დენიან გამტარებზე მომქმედი ამპერის ძალების გამოთვლისას ამპერის კანონში sin α = 1. პარალელური დენების მაგნიტური ურთიერთქმედების კანონიდან გამოდის, რომ R მანძილით დაშორებული I დენიანი გამტარის მაგნიტური ველის ინდუქციის მოდული გამოისახება ფორმულით
\(B=\frac{\mu _{0}}{2\pi }\frac{I}{R}\)
იმისათვის, რომ მაგნიტური ურთიერთქმედების შედეგად პარალელური დენები მიიზიდებოდნენ, ანტიპარალელურები კი განიზიდებოდნენ, სწორი გამტარის ველის მაგნიტური ინდუქციის წირები უნდა იყოს მიმართული საათის ისრის მიმართულებით, თუ შევხედავთ დენის მიმართულებით გამტარის გასწვრივ. სწორი გამტარის მაგნიტური ველის \(\vec{B}\) ვექტორის მიმართულების განსაზღვრისას შეიძლება ბურღის წესის გამოყენება: სახელურის ბრუნვის მიმართულება ემთხვევა \(\vec{B}\) ვექტორის მიმართულებას, თუ ბურღის გადაადგილების მიმართულება ემთხვევა დენის მიმართულებას (ნახ. 3).
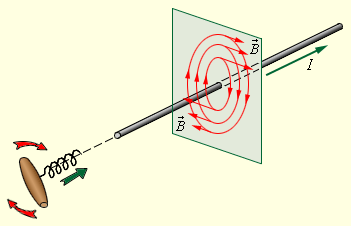
ნახ. 3.
სწორი დენიანი გამტარის მაგნიტური ველი
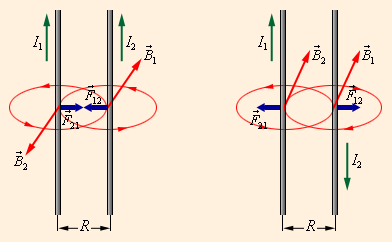
ნახ. .4.
პარალელური და ანტიპარალელური დენების მაგნიტური ურთიერთქმედება
ნახ. 4 განმარტავს პარალელური დენების ურთიერთქმედების კანონს.
დენიანი პარალელური სადენების მაგნიტური ურთიერთქმედება საერთაშორისო ერთეულების სისტემაში გამოიყენება დენის ძალის ერთეულის - ამპერის განსაზღვრისათვის:
ამპერი - უცვლელი დენის ძალაა, რომელიც ვაკუუმში მოთავსებულ, ერთმანეთისაგან 1 მეტრით დაშორებულ, ორ უსასრულოდ გრძელ და უმნიშვნელოდ მცირე წრიული კვეთის დენიან გამტარში გავლისას სიგრძის ყოველ მეტრზე 2·10–7 ნ-ს ტოლი მაგნიტური ძალით ურთიერთქმედების იწვევს.
{loadnavigation}
ელექტროლიტებს უწოდებენ გამტარ გარემოს, რომელშიც ელექრული დენის გავლას თან ახლავს ნივთიერების გადატანა. ელექტროლიტებში თავისუფალი მუხტის მატარებლებს დადებითად და უარყოფითად დამუხტული იონები წარმოადგენენ. ელექტროლიტებს განეკუთვნებიან გამდნარ მდგომარეობაში მყოფი მარავალი მეტალის შენაერთი, და ასევე ზოგიერთი მყარი ნივთიერება. მაგრამ ელექტროლიტების ძირითად წარმომადგენლებს, რომლებსაც ფართოდ იყენებენ ტექნიკაში, არაორგანული მაჟავეების, მარილებისა და ფუძე წყალხსნარები წარმოადგენენ.
ელექტროლიტში ელექტრული დენის გავლას თან ახლავს ელექტროდებზე ნივთიერების გამოყოფა. ამ მოვლენას ელექტროლიზს უწოდებენ.
ელექტროლიტში ელექტრული დენი ორივე ნიშნის იონების ერთმანეთის საწინააღმდეგო მიმართულებით მოძრაობას წარმოადგენს. დადებითი იონები მოძრაობენ უარყოფითი ელექტროდისკენ (კათოდისკენ), უარყოითი იონები კი დადებითი ელექტროდისკენ (ანოდისკენ). იონები მჟავების, მარილებისა და ტუტეების წყალხსნარებში ნაწილი ნეიტრალური მოლეკულების გახლეჩვის შედეგად წარმოიქმნება. ამ მოვლენას ელექტრულ დისოციაციას უწოდებენ. მაგალითად, სპილენძის ქლორიდი, CuCl2 წყალხსნარში დისოცირდება სპილენძისა და ქლორის იონებად:
\(CuCl_{2}\rightleftharpoons Cu^{2+}+2Cl^{-}\)
ელექტროდების დენის წყაროსთან მიერთებისას ელექტრული ველის მოქმედებით იონები იწყებენ მოწესრიგებულ მოძრაობას: სპილენძის დადებითი იონების კათოდისკენ მიემართებიან, ხოლო ქლორის უარყოფითი იონები - ანოდისაკენ (ნახ. .1).
მიაღწევენ რა კათოდს სპილენძის იონები კათოდის ჭარბი ელექტრონებით ნეიტრალდებიან, ნეიტრალურ ატომებად გარდაიქმნებიან და ილექებიან კათოდზე. ქლორის იონები აღწევენ რა ანოდამდე, გასცემენ ერთ ელექტრონს. ამის შემდეგ ქლორის ნეიტრალური ატომები წყვილ-წყვილად ერთდებიან და ქმნიან ქლორის მოლეკულას Cl2. ანოდზე ქლორი ბუშტუკების სახით გამოიყოფა.
ბევრ შემთხვევაში ელექტროლიზს თან ახლავს ელექტროდებზე გამოყოფილი დაშლის პროდუქტების მეორადი რეაქცია ელექტროდების მასალასთან ან გამხსნელთან. მაგალითს წარმოადგენს სპილენძის სულფატის წყალხსანარის CuSO4 (სპილენძის კუპოროსის) ელექტროლიზი იმ შემთხვევაში, როცა ელექტროდები ჩაშვებულია სპილენძისაგან დამზადებულ ელექტროლიტში.
სპილენძის სულფატის მოლეკულების დისოციაცია შემდეგი სქემით ხდება
\(CuSO_{4}\rightleftharpoons Cu^{2+}+SO_{4}^{2-}\)
სპილენძის ნეიტრალური ატომები კათოდზე მყარი ნალექის სახით ედება. ამ გზით ქიმირად სუფთა სპილენძის მიღებაა შესაძლებელი. \(SO_{4}^{2-}\) იონი ანოდს აძლევს ორ ელექტრონს ნეიტრალურ რადიკალად SO4 გადაიქცევა და მეორად რეაქციაში შედის სპილენძის ანოდთან:
SO4 + Cu = CuSO4.
სპილენძის სულფატის წარმოქმნილი მოლეკულა ხსნარში გადადის.
ამგვარად, სპილენძის სულფატის წყალხსანარში ელექტრული დენის გავლისას ხდება სპილენძის ანოდის დაშლა და სპილენძის კათოდზე დალექვა. ამ დროს სპილენძის სულფატის კონცენტარცია არ იცვლება.
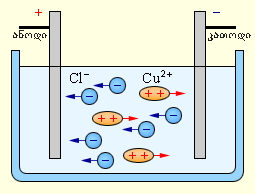
ნახ. 1.
სპილენძის ქლორიდის წყალხსნარის ელექტროლიზი
ელექტროლიზის კანონი ექსპერიმენტულად დაადგინა ინგლისელმა ფიზიკოსმა მ.ფარადეიმ 1833 წელს. ფარადეის კანონი განსაზღვრავს ელექტროლიზის დროს ელექტროდებზე გამოყოფილი პირველადი პროდუქტების რაოდენობას:
ელექტროდზე გამოყოფილი ნივთიერების m მასა ელექტროლიტში გატარებული Q მუხტის პირდაპირპროპორციულია:
m = kQ = kIt.
k სიდიდეს ელექტროქიმიურ ექვივალენტს უწოდებენ.
ელექტროდზე გამოყოფილი ნივთიერების მასა ყველა იმ იონის მასის ტოლია, რომლებმაც ელექტროდამდე მიაღწია:
\(m=m_{0}N=m_{0}\frac{Q}{q_{0}}=\frac{m_{0}}{q_{0}}It\)
აქ m0 და q0 - ერთი იონის მასა და მუხტია, \(N=\frac{Q}{q_{0}}\)- იონების რიცხვი, რომლებმაც ელექტროდამდე მიაღწია ელექტროლიტში Q მუხტის გავლისას. ამგვარად, ელექტროქიმიური ექვივალენტი k ტოლია მოცემული ნივთიერების იონის m0 მასის ფარდობისა მის q0 მუხტთან. რადგანაც იონის მუხტი ნივთიერების n ვალენტობის ელექმენტარული მუხტის e სიდიდეზე ნამრავლის ტოლია (q0 = ne), გამოსახულება ელექტროქიმიური ექვივალენტი k-სათვის შემდეგი სახით ჩაიწერება
\(k=\frac{m_{0}}{q_{0}}=\frac{m_{0}N_{A}}{neN_{A}}=\frac{1}{F}\frac{M}{n}\).
სადაც NA – ავoგადროს მუდმივაა, M = m0NA – ნივთიერების მოლეკულური მასა, F = eNA – ფარადეის მუდმივა.
F = eNA = 96485 კ / მოლი.
ფარადეის მუდმივა რიცხობრივად იმ მუხტის ტოლია, რომელმაც უნდა გაიაროს ელექტროლიტში ელექტროდზე ერთი მოლი ერთვალენტიანი ნივთიერების გამოსაყოფად.
ელექტროლიზისათვის ფარადეის კანონს აქვს სახე:
\(m=\frac{1}{F}\frac{M}{n}It\).
ელექტროლიტის მოვლენა თანამედროვე წარმოებაში fართოს გამოიყენება.
