{loadnavigation}

ელექტრულ ველში შეტანილ ნივთიერებას შეუძლია მნიშვნელოვნად შეცვალოს იგი. ეს იმასთანაა დაკავშირებული, რომ ნივთიერება შედგება დამუხტული ნაწილაკებისაგან. გარე ველის არარსებობის შემთხვევაში ნაწილაკები ნივთერების შიგნით განაწილებულია ისე, რომ მათ მიერ შექმნილი ელექტრული ველი, ატომებისა და მოლეკულების დიდი რაოდენობის შემცველი მოცულობების შორის გასაშუალოებით, ნულის ტოლია. გარე ველის  არსებობის შემთხვევაში ხდება დამუხტული ნაწილაკების გადანაწილება და ნივთიერებაში წარმოიქმნება საკუთარი ელექტრული ველი. სრული \(\vec{E}\) ელექტრული ველი სუპერპოზიციის პრინციპის თანახმად იქმნება \(\vec{E}_{0}\) გარე ველის და ნივთიერების დამუხტული ნაწილაკების მიერ შექმნილი \(\vec{E}{}'\) შიგა ველების შეჯამებით.

ელექტრული თვისებების მიხედვით ნივთიერებები მრავალგვარია. ნივთიერებათა ყველაზე უფრო ფართო კლასებს ქმნიან გამტარები და დიელექტრიკები.

გამტარების ძირითადი განმასხვავებელი თავისებურებაა  თავისუფალი მუხტების (ელექტრონების) არსებობა, რომლებიც სითბურ მოძრაობაში მონაწილეობენ და თავისუფლად შეუძლიათ გადაადგილება გამტარის მთელ მოცულობაში. ტიპური გამტარები - მეტალებია.

გარე ველის არარსებობის შემთხვევაში გამტარის მოცულობის ნებისმიერ ელემენტში უარყოფითი მუხტები ანეიტრალებენ იონური მესერის დადებით მუხტებს. ელექტულ ველში შეტანილ გამტარში ხდება თავისუფალი მუხტების გადანაწილება, რის შედაგადაც გამტარის ზადაპირზე წარმოიქმნება (თავს იყრის) არაკომპენსირებული დადებითი და უარყოფით მუხტები (ნახ. 1). ამ პროცესს ელექტროსტატიკური ინდუქცია ეწოდება, ხოლო გამტარის ზედაპირზე თავმოყრილ მუხტებს - ინდუქციური მუხტები.

 ინდუქციური მუხტები ქმნიან საკუთარ ველს\(\vec{E}{}'\), რომელსაც გამტარის მთელ მოცულობაში ანეიტრალებს \(\vec{E}_{0}\) გარე ველი: \(\vec{E}=\vec{E}_{0}+\vec{E}{}'\) (გამტარის შიგნით).

გამტარის შიგნით სრული ელექტროსტატიკური ველი ნულის ტოლია, პოტენციალები კი ყველა წერტილში ერთნაირია და გამტარის ზედაპირის პოტენციალის ტოლია.

 

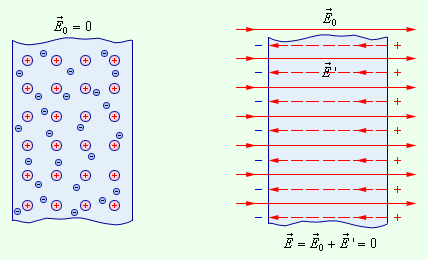
ნახ. 1.

ელექტროსტატიკური ველი

 

ელექტრულ ველში მოთავსებული გამტარის ყველა შიგა არე ელექტრონეიტრალური რჩება. გამტარის შიგნით გამოყოფილი რაღაც მოცულობა რომ მოვაცილოთ და სიცარიელე, ცარიელი სიღრუე რომ წარმოვქმნათ, მაშინ სიღრუის შიგნით ელექტრული ველი ნულის ტოლი იქნება. ამაზეა დაფუძნებული ელექტროსტატიკური დაცვა - ელექტრული ველისადმი მგრძნობიარე ხელსაწყოებს, ველის გავლენის თავიდან ასცილებლად მეტალის ყუთებში ათავსებენ (ნახ. 2).

 

ნახ. 2.

ელექტროსტატიკური დაცვა. მეტალის სიღრუეში ველი ნულის ტოლია

 

რადგანაც გამტარის ზედაპირი ექვიპოტენციურია, ზედაპირთან ძალწირები მისი მართობული უნდა იყოს.

გამტარებისაგან განსხვავებით, დიელექტრიკებში (იზოლატორებში) არა არის თავისუფალი ელექტრული მუხტები. ისინი ნეიტრალური მოლეკულებისა და ატომებისაგან შედგებიან. ნეიტრალურ ატომში დამუხტული ნაწილაკები ერთმანეთთანაა დაკავშირებული და არ შეუძლიათ ელექტრული ველის მოქმედებით იმოძრაონ დიელექტრიკის მთელ მოცულობაში.

დიელექტრიკის \(\vec{E}_{0}\) ელექტრული ველში შეტანისას, მასში ადგილი აქვს მოლეკულებისა და ატომების შემადგენლობაში შემავალი მუხტების გარკვეულ გადანაწილებას. ასეთი გადანაწილების შედაგად დიელექტრიკის ზედაპირზე წარმოიქმნება ჭარბი გაუწონასწორებელი ბმული (ჩამაგრებული, მოძრაობა რომ არ შეუძლია) მუხტები. ჩამაგრებული მუხტების მაკრისკოპულ სტრუქტურების შემადგენლობაში შემავალი დამუხტული ნაწილაკები, ძველებურად თვიანთი ატომების შემადგენლობაში ხვდებიან.

ბმული მუხტები ქმნიან \(\vec{E}{}'\) ელექტრულ ველს, რომელიც დიელექტრიკის შიგნით მიმართულია გარე ველის დაძაბულობის \(\vec{E}_{0}\) ვექტორის საწინააღმდეგოდ. ამ პროცესს დიელექტრიკის პოლარიზაციას უწოდებენ. ამის შედეგად დიელექტრიკის შიგნით სრული ელექტრული \(\vec{E}=\vec{E}_{0}+\vec{E}{}'\) ველი სიდიდით გარე \(\vec{E}_{0}\) ველზე ნაკლები გამოდის.

ფიზიკურ სიდიდეს, რომელიც ტოლია ვაკუუმში გარე \(\vec{E}_{0}\) ელექტრული ველის დაძაბულობის ფარდობისა ერთგვაროვან დიელექტრიკში სრული ველის \(\vec{E}\) დაძაბულობისა, ნივთიერების დიელექტრულ შეღწევადობას უწოდებენ.

 \(\varepsilon =\frac{E_{0}}{E}\)

დიელექტრიკის პოლარიზების რამდენიმე მექანიზმი არსებობს. მათ შორის ძირითადებია ორიენტაციული და ელექტრული პოლარიზაციები. ეს მექანიზმები თავს იჩენენ ძირითადად აიროვანი და თხევადი დიელექტრიკების პოლარიზაციისას.

ორიენტაციული ან დიპოლური პოლარიზაცია ე.წ. პოლარულ დიელექტრიკებში  წარმოიშვება, სადაც დადებითი და უარყოფითი მუხტების განაწილების ცენტრები ერთმანეთს არ ემთხვევა. ასეთი მოლეკულები მიკროსკოპულ ელექტრულ დიპოლებს  - მოდულით ტოლ და ნიშნით საწინააღმდეგო, ერთმანეთისაგან გარკვეულ მანძილზე განლაგებული ორი მუხტის ერთობლიობას წარმოადგენენ. დიპოლური მომენტი აქვს, მაგალითად, წყლის მოლეკულას და ასევე სხვა დიელექტრიკების მოლეკულებსაც (H₂S, NO₂  და ა.შ.).

გარე ელექტრული ველის არარსებობის შემთხვევაში მოლეკულური დიპოლების ღერძები, სითბური მოძრაობის გამო, ქაოსურადაა ორიენტირებული, ასე რომ დიელექტრიკის ზედაპირზე და მისი  მოცულობის ნებისმიერ ელემენტში მუხტი საშუალოდ ნულის ტოლია.

დიელექტრიკის \(\vec{E}_{0}\) გარე ველში შეტანით მოლეკულური დიპოლების ნაწილობდივი ორიენტაცია წარმოიქმნება. ამის შედეგად დიელექტრიკის ზედაპირზე იქმნება გაუწონასწირებელი (არაკომპენსირებული) მაკრისკოპული ბმული მუხრები, რომლებიც \(\vec{E}_{0}\) გარე ველის შემხვედრი მიმართულების \(\vec{E}{}'\) ველს ქმნიან (ნახ. 3).

 ნახ. 3.

პოლარული დიელექტრიკის პოლარიზაციის ორიენტაციის მექანიზმი

პოლარული დიელექტრიკების პოლარიზაცია ძლიერადაა დაკავშირებული ტემპერატურაზე, რადგანაც მოლეკულების სითბური მოძრაობა მადეზორიენტირებელ ფაქტორს წარმოადგენს.

ელექტრული ან დრეკადი მექანიძზმი თავს იჩენს ე.წ. არაპოლარული დიელექტრიკების პოლარიზაციის დროს, რომელთა მოლეკულებს გარე ველის არარსებობის შემთხვევაში დიპოლური მომენტი არ აქვთ. ელექტრული ველის მოქმედებისას არაპოლარული დიელექტრიკების მოლეკულები დეფორმირდებიან - დადებითი მუხტები გადანაცვლდებიან \(\vec{E}_{0}\) ვექტორის მიმართულებით, უარყოფითები კი საწინააღმდეგო მიმართულებით. ამის შედეგად მოლეკულები ელექტრულ დიპოლებად იქცევიან, რომლის ღერძიც გარე ველის გასწვრივაა მიმართული. დიელექტრიკის ზედაპირზე წარმოიქმნება არაკომპენსირებული ბმული მუხტები, რომლებიც ქმნიან \(\vec{E}_{0}\) გარე ველის საწინააღმდეგოს მიმართულ საკუთარ \(\vec{E}{}'\) ველს. ამგვარად ხდება არაპოლარული დიელექტრიკის პოლარიზაცია (ნახ. 4).

გარე ელექტრული ველის მოქმედებით გამოწვეული არაპოლარული დიელექტრიკების პოლარიზაცია არ არის დამოკიდებული სითბურ მოძრაობაზე, ამოტომ არაპოლარული დიელექტრიკის პოლარიზაცია არ არის დამოკიდებული ტემპერატურაზე. არაპოლარული დიელექტრიკის მოლეკულის მაგალითად გამოდგება CH₄  მეთანის მოლეკულა. ამ მოლეკულაში წესიერი პირამიდის ცენტრში  ოთხჯერიონიზებული ნახშირბადის იონია მოთავსებული, ხოლო წვეროებში წყალბადის იონებია განლაგებული. გარე ელექტრულ ველში მოხვედრისას ნახშირბადის იონი პირამიდის ცენტრიდან გადაინაცვლებს, და მოლეკულას გარე ელექტრული ველი პროპორციული დიპოლური მომენტი უჩნდება.

 

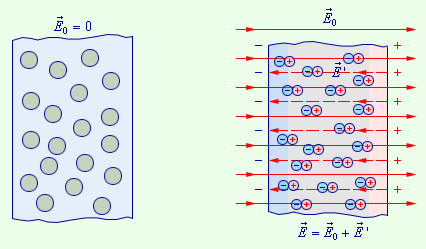
 ნახ. 4.

არაპოლარული დიელექტრიკის პოლარიზაცია

 

პოლარული და არაპოლარული დიელექტრუკების პოლარიზაციისას წარმოქმნილი, ბმული მუხტების \(\vec{E}{}'\) ელექტრული ველს მოდული \(\vec{E}_{0}\) გარე ველის მოდულის პროპორციულად იცვლება. ძალიან ძლიერ ელექტრულ ველებში ეს კანონზომიერება შეიძლება დაირღვეს, და ასეთ შემთხვევაში წარმოიშვება სხვადასხვა არაწრფივი ეფექტი. პოლარული დიელექტრიკების შემთხვევაში შეიძლება დაიკვირვებოდეს გაჯერების ეფექტი, როცა ყველა მოლეკულური დიპოლი ძალხაზების გასწვრის მწკრივდება. არაპოლარული დიელექტრიკების შემთხვევაში ძლიერ გარე ელექტრულ ველს, რომელიც მოდულით შიგა ველთან შედარებადია, შეუძლეა ნივთიერების მოლეკულებისა და ატომების მნიშვნელოვანი დეფორმირება და მათი ელექტრული თვისებების შეცვლა. მაგრამ, ეს მოვლენები პრაქტიკულად არასდროს არ დაიკვირვება, რადგანაც ამისთვის საჭიროა 10¹⁰–10¹² ვ/მ რიგის დაძაბულობის ველები. ამასთან, გაცილების ნაკლები გაძაბულობისას ხდება დიელექტრიკის გარღვევა.

მრავალი არაპოლარული მოლეკულის პოლარიზაციის დროს ხდება მათი ელექტრული გარსის დეფორმირება, ამიტომ ამ მექანიზმმა მიიღო ელექტრული პოლარიზაციის სახელწოდება. ეს მექანიზმი უნივერსალურია, რადგანაც გარე ველის მოქმედებით ელექტრული გარსების დეფორმირება ნებისმიერი დიელექტრიკის ატომებში, მოლეკულებსა და იონებში ხდება.

მყარკრისტალიანი დიელექტრიკების შემთხვევაში წარმოიქმნება ე.წ. იონური პოლარიზაცია, რომლის დროსაც კრისტალური მესერის შემადგენელი სხვადასხვა ნიშნიანი იონები, გარე ელექტრულ ველში მოხვედრისას ურთიერთსაწინააღმდეგო მიმართულებით გადანაცვლდებიან, რის შედეგადაც კრისტალის წახნაგებზე წარმოიქმნება ბმული (არაკომპენსირებული) მუხტები. ასეთი მექანიზმის მაგალითად შეიძლება გამოვიყენოთ NaCl-ს კრისტალის პოლარიზაცია, რომელშიც Na⁺ და Cl^– იონები ერთმანეთში ჩაწყობილ, ორ ქვემესერს ქმნის. გარე ველის არარსებიბის შემთხვევაში NaCl-ს კრისტალის ყოველი ელემეტარული უჯრედი ელექტრულად ნეიტრალურია და არ გააჩნია დიპოლური მომენტი. გარე ელექტრულ ველში ორივე ქვემესერი ურთიერთსაწინააღმდეგოდ გადაინაცვლებს, ე.ი. კრისტალი პოლარიზდება.

არაერთგვაროვანი დიელექტრიკის პოლარიზაციისას ბმული მუხტები შეიძლება წარმოიქმნას არა მხოლოდ დიელექტრიკის ზედაპირზე, არამედ მისი მიცულობის შიგნითაც. ასეთ შემთხვევაში ბმული მუხტების ელექტრულ \(\vec{E}{}'\) ველს და სრულ \(\vec{E}\) ველს შეიძლება, დიელექტრიკის სტრუქტურაზე დამოკიდებული,  რთული სტრუქტურა ჰქონდეთ. იმის მტკიცება, რომ დიელექტრიკში ელექტრული ველი \(\vec{E}\) მოდულით \(\varepsilon\)-ჯერ ნაკლებია \(\vec{E}_{0}\) გარე ველთან შედარებით, მხოლოდ ისეთი ერთგავაროვანი დიელექტრიკების შემთხვავაშია მკაცრად სამართლიანი, რომლებიც იმ მთელ სივრცეს ავსებენ, რომელშიც გარე ველია შექმნილი. კერძოდ:

თუ \(\varepsilon\) დიელექტრიკული შეღწევადობის ერთგვაროვან დიელექტრიკში იმყოფება წერტილოვანი \(Q\) მუხტი, მაშინ ამ მუხტის მიერ შექმნილი ველის დაძაბულობა \(\vec{E}\) და \(\varphi\) პოტენციალი \(\varepsilon\)-ჯერ ნაკლებია ვაკუუმთან შედარებით:

\(\vec{E}=\frac{1}{4\pi \varepsilon _{0}}\frac{Q}{\varepsilon r^{3}}\),       \(\varphi =\frac{1}{4\pi \varepsilon _{0}}\frac{Q}{\varepsilon r}\)

{loadnavigation}

ელქტრულ ველში საცდელი q მუხტის გადაადგილებისას ელექტრული ძალები ასრულებენ მუშაობას.  ეს მუშაობა მცირე \(\Delta\vec{l}\) გადაადგილებისას ტოლია (ნახ. 1):

\(\Delta A=F\cdot\Delta l\cdot\cos\alpha=Eq\Delta l\cos\alpha=E_{1}q\Delta l.\)

 

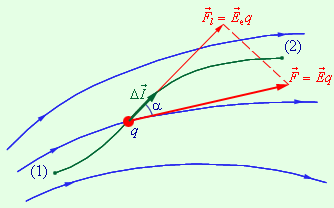
ნახ. 1.

ელექტრული ძალების მუშაობა q მუხტის მცირე \(\Delta\vec{l}\) გადაადგილებისას

 

განვიხილოთ დროში უცვლელად განაწილებული მუხტის მიერ შექმნილი ელექტრული ველის ძალების მუშაობა, ე.ი. ელექტროსტატიკური ველის მუშაობა.

ელექტროსტატიკურ ველს მნიშვნელოვანი თვისება აქვს:

ელექტროსტატუკური ველში ერთი წერტილიდან მეორეში მუხტის გადაადგილებისას ველის ძალების მუშაობა არ არის დამოკიდებული ტრაექტორიის ფორმაზე, და განისაზღვრება მხოლოდ საწყისი და საბოლოო წერტილების მდებარეობასა და ამ მუხტის სიდიდეზე.

ანალოგიური თვისება აქვს გრავიტაციულ ველსაც და ამაში არაფერია გასაკვირი, რადგანაც გრავიტაციული და კულონური ძალები მსგავსი ფორმულით  აღიწერება.

მუშაობის ტრაექტორიის ფორმისაგან დამოუკიდებლობის შედეგია შემდეგი მტკიცება:

ელექტროსტატიკური ველის ძალების მუშაობა მუხტის ნებისმიერ ჩაკეტილ ტრაექტორიაზე გადაადგილებისას ნულის ტოლია.

ძალურ ველებს, რომლებსაც ეს თვისება აქვთ, პოტენციურ ან კონსერვატორულს უწოდებენ.

ნახ. 2-ზე გამოსახულია Q წერტილოვანი მუხტის კულონური ველის ძალწირები და საცდელი q მუხტის საწყისი (1)  წერტილიდან საბოლოო  (2) წერტილში გადაადგილების ორი განსხვავებული ტრაექტორია.  ერთერთ ტრაექტორიაზე გამოყოფილია მცირე გადაადგილება \(\Delta\vec{l}\). ამ გადაადგილებაზე კულონური ძალების მუშაობა ΔA  ტოლია

 \(\Delta A=F\Delta l\cos\alpha=Eq\Delta r=\frac{1}{4\pi\varepsilon_{0}}\frac{Qq}{r^{2}}\Delta r.\)

ამგვარად, მუშაობა მცირე გადაადგილებაზე დამოკიდებულია მუხტებს შორის r  მანძილსა და მის Δr ცვლილებაზე. თუ ამ გამოსახულებას r = r₁-დან r = r₂-მდე ინტერვალში გავაინტეგრალებთ, მივიღებთ

\(A=\int_{r_{1}}^{r_{2}}E\cdot q\cdot dr=\frac{Qq}{4\pi\varepsilon_{0}}\left (\frac{1}{r_{1}}-\frac{1}{r_{2}} \right ).\)

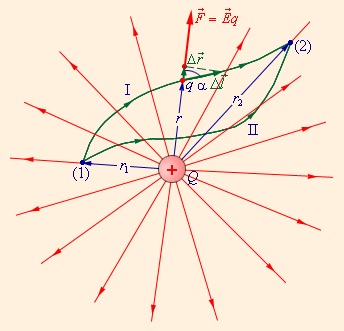
ნახ. 2.

q მუხტის გადაადგილებისას კულონური ძალების მუშაობა დამოკიდებულია მხოლოდ ტრაექტორიის საწყის და საბოლოო წერტილებამდე r₁ და r₂  მანძილებზე

 

მიღებული შედეგი არ არის დამოკიდებული ტრაექტორიის ფორმაზე. ნახ. 2- ზე I და II ტრაექტორიებზე კულონური ძალების მუშაობა ერთნაირია. თუ ერთ-ერთ ტრაექტორიაზე საცდელი q მუხტის გადაადგილების მიმართულებას შევცვლით, მუშაობა ნიშანს შეიცვლის. აქედან გამომდინარეობს, რომ ჩაკეტილ ტრაექტორიაზე კულონური ძალების მუშაობა ნულის ტოლია.

 

თუ ელექტროსტატიკური ველი შექმნილია  \(Q_{i}\) წერტილოვანი მუხტების ერთობლიობით, მაშინ საცდელი q მუხტის გადაადგილებისას ჯამური ველის A მუშაობა,  სუპერპოზიციის პრინციპის თანახმად,  წერტილოვანი მუხტების კულონური \(A_{i}\) ველების აჯამვით მიიღება: \(A=\sum A_{i}\). რადგანაც ჯამის არცერთი წევრი \(A_{i}\) ტრაექტორიის ფორმაზე დამოკიდებული არ არის, არც ჯამური ველის A მუშაობაა ტარექტორიაზე დამოკუდებული, არამედ დამოკიდებულია მხოლოდ საწყისი და საბოლოო წერტილების მდებარეობაზე.

 

ელექტროსტატიკური ველის პოტენციურობის თვისება მუხტის პოტენციური ენერგიის ცნების შემოტანის საშუალებას იძლევა. ამისათვის სივრცეში უნდა აირჩეს რაღაც (0) წერტილი და ამ წერტილში მოთავსებული q მუხტის პოტენციური ენერგია უნდა ჩაითვალოს ნულის ტოლად.

სივრცის ნებისმიერ (1) წერტილში მოთვსებული q მუხტის პოტენციური ენერგია ფიქსირებული (0) წერტილის მიმართ იმ A₁₀  მუშაობის ტოლია, რომელსაც ელექტროსტატიკური ველი ასრულებს მუხტის (1) წერტილიდან (0) წერტილში გადასაადგილებლად:

W_p1 = A_10.

(ელექტროსტატიკაში ენერგიას აღნიშნავენ W ასოთი, რადგანაც E ასოთი დაძაბულობის აღნიშვნაა მიღებული.)

მექანიკის მსგავსად, პოტენციური ენერგია განისაზღვრება მუდმივი სიდიდის სიზუსტით, რომელიც საყრდენი (0) წერტილის შერჩევაზეა დამოკიდებული. პოტენციური ენერგიის  ასეთი არაცალსახა განსაზღვრა გარკვეულ გაუგებრობებს იწვევს, რადგან ფიზიკური აზრი აქვს არა თვით პოტენციურ ენერგიას არამედ ორ წერტილს შორის მისი მნიშვნელობების სხვაობას.

წერტილოვანი q მუხტის (1)  წერტილიდან (2) წერტილში გადაადგილებისას ელექტროსტატიკური ველის მიერ შესრულებული მუშაობა ტოლია ამ წერტილებში პოტენციური ენერგიების სხვაობისა და არარის დამოკიდებული გადაადგილების ტრაექტორიასა და (0) წერტილის არჩევაზე.

A₁₂ = A₁₀ + A₀₂ = A₁₀ – A₂₀ = W_p1 – W_p2.

ელექტროსტსტიკურ ველში მოთავსებული q მუხტის პოტენციური ენერგია ამ მუხტის სიდიდის პროპორციულია.

ფიზიკური სიდიდე, რომელიც ტოლია ელექტროსტატიკურ ველში ელექტრული მუხტის პოტენციური ენერგიის ფარდობისა ამ მუხტის სიდიდესთან, ელექტრული ველის პოტენციალს უწოდებენ:

\(\varphi=\frac{W_{p}}{q}.\)

პოტენციალი φ ელექტროსტატიკური ველის ენერგეტიკულ მახასიათებელს წარმოადგენს.

ელექტრული q მუხტის საწყისი (1) წერტილიდან საბოლოო (2) წერტილში გადაადგილების A₁₂ მუშაობა ტოლია მუხტის სიდიდის ნამრავლისა საწყისის და საბოლოო წერტილების პოტენციალთა სხვაობაზე (φ₁ – φ₂):

A₁₂ = W_p1 – W_p2 = qφ₁ – qφ₂ = q(φ₁ – φ₂).

საერთაშორისო სი სისტემაში პოტენციალის ერთეულია ვოლტი (ვ).

1 ვ = 1 ჯ / 1 კ.

ელექტროსატატიკის ბევრ ამოცანაში  პოტენციალის გამოთვლისას ხელსაყრელია საყრდენ წერტილად უსასრულოდ დაშორებული წერტილის აღება. ასეთ შემთხვევაში პოტენციალის ცნება შეიძლება შემდეგნაირად ჩამოყალიბდეს:

სივრცის მოცემულ წერტილში ველის პოტენციალი ტოლია იმ მუშაობისა, რომელსაც ასრულებენ ელექტრული ძალები ერთეულოვანი დადებითი მუხტის მოცემული წერტილიდან უსასრულობაში გადასაადგილებლად.

   \(\varphi_{\infty}=\frac{A_{\infty}}{q}.\)

წერტილოვანი Q მუხტის ველის  φ_∞    პოტენციალი მისგან r  მანძილზე უსასრულოდ დაშორებული წერტილის მიმართ შემდეგნაირად გამოითვლება:

\(\varphi=\varphi_{\infty}=\frac{1}{q}\int_{r}^{\infty}Edr=\frac{Q}{4\pi\varepsilon_{0}}\int_{r}^{\infty}\frac{dr}{r^{2}}=\frac{1}{4\pi\varepsilon_{0}}\frac{Q}{r}.\)

გაუსის თეორემიდან გამომდინარე, ეს ფორმულა გამოსახავს ერთგვაროვნად დამუხტული ბურთულის (ან სფეროს) ველის პოტენციალს, როცა r ≥ R, სადაც R - ბურთულის რადიუსია.

ელექტროსტატიკური ველის თვალნათლივ წარმოდგენისათვის ძალწირების გვერდით ექვიპოტენციალური ზედაპირები გამოიყენება.

ზედაპირი, რომლის ყოველ წერტილში ელექტრული ველის პოტენციალს ერთნაირი მნიშვნელობა აქვს ექვიპოტენციური ზედაპირი ან ტოლი პოტენციალების ზედაპირი ეწოდება.

ელექტროსტატიკური ველის ძალწირები ყოველთვის ექვიპოტენციური ზედაპირების მართობულია.

წერტილოვანი მუხტის კულონური ველის ექვიპოტენციური ზედაპირები - კონცენტრული სფეროებია. ნახ. 3-ზე ზოგიერთი უბრალო ელექტრული ველების ექვიპოტენციური ზედაპირები  და ძალწირებია წარმოდგენილი.

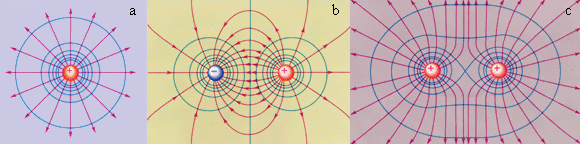
ნახ. 3.

უბრალო ელექტრული მუხტების ექვიპოტენციური ზედაპირები (ლურჯი ხაზები) და ძალწირები (წითელი ხაზები):  a - წერტილოვანი მუხტი;  b - ელექტრული დიპოლი:  c - ორი ტოლი დადებითი მუხტი

 

ერთგვაროვანი ველის შემთხვევაში ექვივალენტური ზედაპირები პარალელური სიბრტყეების სისიტემას წარმოადგენს.

თუ საცდელმა q მუხტმა შეასრულა ძალწირის გასწვრივ მცირე \(\Delta\vec{l}\) გადაადგილება  (1) წერტილიდან (2) წერტილში, შეიძლება ჩავწეროთ:

ΔA₁₂ = qEΔl = q(φ₁ – φ₂) = – qΔφ,

 სადაც Δφ = φ₁ – φ₂ – პოტენციალი ცვლილებაა. აქედან გამოდის 

\(E=-\frac{\Delta\varphi}{\Delta l};\: (\Delta l\to 0)\)  ან \(E=-\frac{d\varphi}{dl}.\)

ეს ფორმულა ველის დაძაბულობასა და პოტენციალს შორის კავშირს სკალარულად გამოსახავს. აქ  l  - ძალწირის გასწვრივ ათვლილი ძალწირის კოორდინატაა.

ელექტრული მუხტების ველების დაძაბულობების სუპერპოზიციის პრინციპიდან გამომდინარეობს პოტენციალების სუპერპოზოციის პრინციპი:

φ = φ₁ + φ₂ + φ₃ + ...

{loadnavigation}

ექსპერიმენტულად დადგენილი კულონის კანონი და სუპერპოზიციის პრინციპი, ვაკუუმში მუხტების მოცემული სისტემის ელექტროსტატიკური ველის სრულად აღწერის საშუალებას იძლევა. მაგრამ, ელექტროსტატიკური ველის თვისებები შეიძლება გამოისახოს სხვა, უფრო ზოგადი ფორმით, წერტილოვანი კულონის ველების წარმოდგენის გამოყენების გარეშე.

შემოვიტანოთ ელექტრული ველის მახასიათებელი ახალი ფიზიკური სიდიდე - ელექტრული ველის დაძაბულობის ვექტორის Φ ნაკადი. ვთაქვათ სივრცეში, სადაც შექმნილია ელექტრული ველი, გვაქვს რაღაც საკმარისად მცირე ΔS ფართობი. \(\vec{E}\) ვექტორის მოდულის ნამრავლი ΔS ფართობზე და \(\vec{E}\) ვექტორსა და ამ ფართიბის \(\vec{n}\) ნორმალს შორის α კუთხის კოსინუსზე ΔS ფართობში გამავალ დაძაბულობის ვექტორის ელემენტარულ ნაკადს უწოდებენ (ნახ. 1):

ΔΦ = E ΔS cos α = E_n ΔS,

სადაც E_n -  \(\vec{E}\)  ვექტორის ნორმალური მდგენელია

 

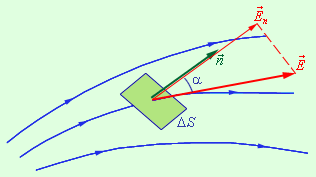
ნახ. 1.

ΔΦ ელემენტარული ნაკადის განმარტებისათვის

 

ახლა განვიხილოთ რაიმე ნებისმიერად აღებული შემოსაზღვრული S ზედაპირი. თუ ამ ზედაპირს დავყოფთ მცირე ΔS_iფართობებად, გამოვთვლით ამ ფართობების გამჭვოლავი \(\vec{E}\) ველის ΔΦ_i ნაკადებს, შემდეგ კი მათ ავჯამავთ, მივიღბთ S  ზედაპირში გამავალი \(\vec{E}\)  ვექტორის Φ ნაკადს (ნახ. 2):

\(\Phi=\sum\Delta\Phi_{i}=\sum E_{ni}\Delta S_{i}\)

შემოსაზღვრული ზედაპირის შემთხვევაში ყოველთვის გამოიყენება გარე ნორმალი.  

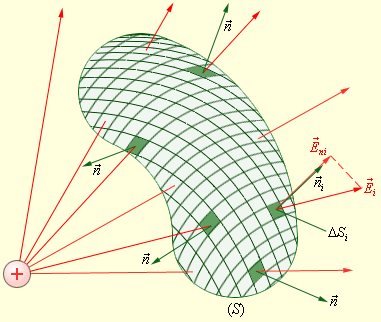
ნახ. 2.

შემთხვევით აღებულ ჩაკეტილ S ზედაპირში გამავალი Ф ნაკადის გამოთვლა

 

გაუსის თეორემა ამტკიცებს, რომ:

ნებისმიერად აღებული შემოსაზღვრული   ზედაპირის გამჭოლი \(\vec{E}\) ელექტროსტატიკური ველის დაძაბულობის ვექტორის ნაკადი ტოლია ამ ზედაპირის შიგნით განლაგებული მუხტების ალგებრული ჯამის განაყოფისა ელექტროლ მუდმივაზე ε₀.

\(\Phi=\frac{1}{\varepsilon_{0}}\sum q_{shinagani}\)

დამტკიცებისათვის ჯერ განვიხილოთ S სფერული ზედაპირი, რომლის ცენტრშიც q მუხტია მოთავსებული. ელექტრული ველი სფეროს ნებისმიერ წერტილში მისი ზედაპირის პროპორციულია და მოდულით ტოლია:

\(E=E_{n}=\frac{1}{4\pi\varepsilon_{0}}\frac{q}{R^{2}},\)

სადაც R – სფეროს რადიუსია. სფეროს ზედაპირში გამავალი Φ ნაკადი  ტოლი იქნება E-ს ნამრავლისა სფეროს ზედაპირის 4πR² ფართობზე. აქედან გამომდინარე,

\(\Phi=\frac{1}{\varepsilon_{0}}q.\)

ახლა წერტილოვანი მუხტი შემოვსაზღვროთ ნებისმიერად აღბული S ზედაპირით და განვიხილოთ დამხმარე სფერო R₀ რადიუსით (ნახ. 3).

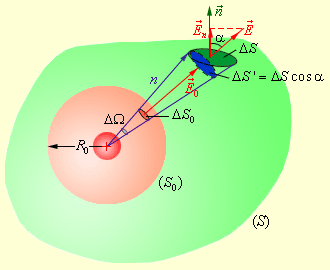
ნახ. 3.

წერტილოვანი მუხტის გარშემო ნებისმიერად აღებულ ფართობში გამავალი    ელექტრული ველის ნაკადი

 

განვიხილით კონუსი წვეროში მცირე სივრცული ΔΩ კუთხით. ეს კონუსი სფეროს ზედაპირზე გამოჰყოფს მცირე ΔS₀  ფართობს, ხოლო S ზედაპირზე - ΔS ფართობს. ამ ფართობების განმსჭვალავი ელემენტარული ΔΦ₀ და ΔΦ ნაკადები ერთნაერია. მართლაც,

ΔΦ₀ = E₀ΔS₀,   ΔΦ = EΔS cos α = EΔS '.

აქ ΔS' = ΔS cos α – ფართობია, რომელსაც წვეროში მცირე სივრცული ΔΩ კუთხის მქონე კონუსი გამოყოფს n რადიუსიან სფეროზე. 

რადგან  \(E_{0}/E=r^{2}/R_{0}^{2}\) , ხილო  \(\Delta S_{0}/\Delta S^{'}=R_{0}^{2}/r^{2}\) ე.ი.  \(\Delta\Phi_{0}=\Delta\Phi.\) აქედან გამოდის, რომ ნებისმიერად აღებული ზედაპირის განმსჭვალავი, ამ ზედაპირის შიგნით მოქცეული, წერტილოვანი მუხტის ელექტრული ველის სრული ნაკადი ტოლია დამხმარე სფეროს ზედაპირში გამავალი Φ₀ ნაკადისა:

\(\Phi=\Phi_{0}=\frac{q}{\varepsilon_{0}}.\)

ანალიგიურად შეიძლება ჩვენაბა, რომ თუ ჩაკეტილი S  ზედაპირი არ მოიცავს წერტილოვან q მუხტს, ნაშინ ნაკადი Φ = 0. ასეთ შემთხვევა მოცემულია ნახ. 2-ზე. წერტილოვანი მუხტის ელექტრული ველის ყველა ძალწირი სრულად განსჭვალავს S  ზედაპირს. S ზედაპირის შიგნით მუხტი არ არის, ამიტომ ამ არეში ძალწირები არც წყდება და არც წარმოიქმნება (იწყება) arabmenhealth.com.

გაუსის თეორემის განზოგადება შემთხვევითად განაწილებული მუხტებისათვის სუპერპოზისიის პრიციპიდან გამომდინარეობს. მუხტების შემთხვევითი განაწილება შეიძლება წარმოვადგინით წერტილოვანი მუხტების  \(\vec{E_{i}}\) ელექტრული ველების ვექტორული ჯამი. შემთხვევითი ჩაკეტილი S ზედაპირის მუხტების სისტემის Φ ნაკადის მიიღება ცალკეული მუხტების ელექტრული ველების Φ_i  ნაკადების აჯამვით. თუ  მუხტი S ზედაპირის შიგნითაა, მაშინ ის ნაკადში იძლევა \(q_{i}/\varepsilon_{0}\) -ის ტოლ წილს; თუ ეს მუხტი გარეთაა მაშინ მისი ელექტრული ველის წილი ნულის ტოლია.

ამგვარად, გაუსის თეორემა დამტკიცებულია.

გაუსის თეორემა კულონის კანონისა და სუპერპოზიციის პრინციპის შედეგს წარმოადგენს. მაგრამ თუ ამ თეორემის  მტკიებას  საწყის აქსიომად მივიღებთ, მაშინ კულონის კანონი მისი შედეგი აღმოჩნდება. ამიტომაც გაუსის თეორემას ხანდახან კულონის კანონის ალტერნატიულ ფორმულირებასაც უწოდებენ.

ხშირ შემთხვევაში, გაუსის თეორემის გამოყენებით შეიძლება ადვილად გამოითვალოს დამუხტული სხეულის ირგვლის ელექტრული ველის დაძაბულობა, თუ მუხტების მოცემული განაწილება რაიმენაირ სიმეტრიას ემორჩილება და ველის საერთო სტრუქტურა შესაძლებელია წინასწარ იქნეს შეცნობილი.

მაგალითად შეიძლება იქნეს გამოყენებული ერთგვაროვნად დამუხტული, გრძელი, R რადიუსის მქონე ცილინდრის ველის გამოთვლა. ამ ამოცანაში გვაქვს ღერძული სიმეტრია. სიმეტრიიდან გამომდინარე ელექტრული ველი მიმართული უნდა იყოს რადიუსის გასწვრივ. ამიტომ გაუსის თეორემის გამოსაყენებლად ხელსაყრელია განვიხილოთ იგივე ღერძის მქონე ჩაკეტილი, ორივე მხარიდან  დახურული, r რადიუსისა და l სიგრძის მქონე ცილინრული S ზედაპირი.

ნახ. 1.3.4.

ერთგავაროვნად დამუხტული ცილინდრის ველის გამოთვლა.  OO'  - სიმეტრიის ღერძია.

 

როცა r ≥ R დაძაბულობის ვექტორის სრული ნაკადი გაივლის ცილინდის გვერდით ზედაპირში, რომლის ფართობიც 2πrl, რადგანაც ორივე ფუძეში გამავალი ნაკადები ნულის ტოლია. გაუსის თეორემის გამოყენება იძლევა:

\(\Phi=E2\pi rl=\frac{\tau l}{\varepsilon_{0}},\)

სადაც \(\tau\) – ცილინდრის სიგრძის ერთეულის მუხტია. აქედან 

\(E=\frac{\tau}{2\pi\varepsilon_{0}r}.\)

ეს შედეგი არ არის დამოკიდებული დამუხტული ცილინდრის რადიუსზე, ამიტომ მისი გამოყენება შესაძლებელია გრძელი ერთგვაროვნად დამუხტული ძაფის შემთხვევაშიც.

დამუხტული ცილინდრის შიგნით ველის დაძაბულობის განსაზღვრისთვის უნდა აიგოს ჩაკეტილი ზედაპირი  r < R შემთხვევისათვის. სიმეტრიის გამო გაუსის ცილინდრის გვერდითი ზედაპირის განმსჭვალავი დაძაბულობის ვექტორის ნაკადის ამოცანა ამ შემთხვევაშიც ტოლია Φ = E 2πrl. გაუსის თეორამის თანახმად, ეს ნაკადი ამ ზედაპირის შიგნით მოქცეული მუხტის პროპორციულია. ეს მუხტი ნულის ტოლია. აქედან გამომდინარეობს, რომ ერთგავაროვნად დამუხტული გრძელი ღრუ ცილინდრის შიგნით ელექტრული ველი ნულის ტოლია.

 ანალოგიურად, გაუსის თეორემა შეიძლება გამოყენებულ იქნას ელექტრული ველის  განსაზღვრისას ისეთ  შემთხვევებში, როცა მუხტების განაწილებას რაიმე სიმეტრია აქვს, მაგალითად, ცენრტის, სიბრტყის ან ღერძის მიმართ  სიმეტრია. ყოველ ასეთ შემთხვევაში უნდ არჩეულ იქნეს შესაბამისი ფორმის ჩაკეტილი გაუსის ზედაპირი. მაგალითად, ცენტრალური სიმეტრიის შემთხვევაში ხელსაყრელია სფერული ფორმის გაუსის ზედაპირი, რომლის ცენტრიც სიმეტრიის ცენტრს ემთხვევა. ღერძული სიმეტრიისას უნდა აირჩეს  ორივე მხრიდან ჩაკეტილი ცილინდრული ზედაპირი, რომლის ღერძიც სიმეტრიის ღერძს ემთხვევა (ზევით განხილულ შემთხვევაში). თუ მუხტის განაწილება არანაირ სიმეტრიას არ ემორჩილება და ელექტტული ველი საერთო სტრუქრურის გამოცნობა შეუძლებელია, გაუსის თეორემის გამოყენება ვერ გაამარტივებს ველის დაძაბულობის განსაზღვრის ამოცანას.

განვიხილოთ მუხტების განაწილების კიდევ ერთი სიმეტრიის მაგალითი - ერთგვაროვნად დამუხტული სიბრტყის ველის განსაზღვრა (ნახ. 5).

 

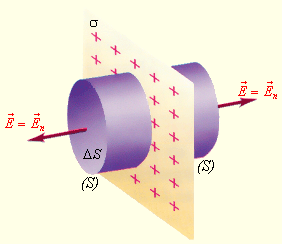
ნახ. 5.

ერთგვაროვნად დამუხტული სიბრტყის ველი. σ  - მუხტის ზედაპირული სიმკვრივე. S  - ჩაკეტილი გაუსის ზედაპირი

 

ამ შემთხვევაში გაუსის ზედაპირად S მიზანშეწონილია გარკვეული სიგრძის ორივე მხრიდან დახურული, ცილინრის არჩევა. ცილინდრის ღერძი დამუხტული ზედაპირის მართობულადაა მიმართული, ხოლო მისი ბოლოები ტოლი მანძილებითაა დაშორებული მისგან. სიმეტრიულობის გამო ერთგავაროვნად დამუხტული სიბრტყის ველი ყველგან ნორმალის გასწვრივ უნდა იყოს მიმართული. გაუსის თეორემის გამოყენება იძლევა:

\(2E\Delta S=\frac{\sigma\Delta S}{\varepsilon_{0}}\) ან \(E=\frac{\sigma}{2\varepsilon_{0}},\)

სადაც σ – მუხტის ზედაპირული სიმკვრივე, ე.ი. ფართობის ერთეულზე მოსული მუხტი.

ერთგვაროვნად დამუხტული სიბრტყის ელექტრული ველისათვის მიღებული გამოსახულება მისაღებია სასრული ზომის ბრტყელი დამუხტული ფართობებისთვისაც. ასეთ შემთხვევაში მანძილი იმ წერტილიდან, რომელშიც უნდა განისაზღვროს ველი დაძაბულობა, დამუხტულ ფართობამდე გაცილებით ნაკლები უნდა იყოს ფართობის ზომებზე.