ელქტრულ ველში საცდელი q მუხტის გადაადგილებისას ელექტრული ძალები ასრულებენ მუშაობას. ეს მუშაობა მცირე \(\Delta\vec{l}\) გადაადგილებისას ტოლია (ნახ. 1):
\(\Delta A=F\cdot\Delta l\cdot\cos\alpha=Eq\Delta l\cos\alpha=E_{1}q\Delta l.\)
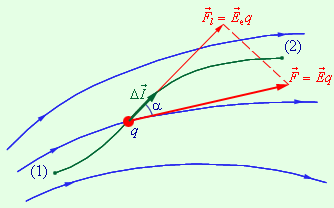
ნახ. 1.
ელექტრული ძალების მუშაობა q მუხტის მცირე \(\Delta\vec{l}\) გადაადგილებისას
განვიხილოთ დროში უცვლელად განაწილებული მუხტის მიერ შექმნილი ელექტრული ველის ძალების მუშაობა, ე.ი. ელექტროსტატიკური ველის მუშაობა.
ელექტროსტატიკურ ველს მნიშვნელოვანი თვისება აქვს:
ელექტროსტატუკური ველში ერთი წერტილიდან მეორეში მუხტის გადაადგილებისას ველის ძალების მუშაობა არ არის დამოკიდებული ტრაექტორიის ფორმაზე, და განისაზღვრება მხოლოდ საწყისი და საბოლოო წერტილების მდებარეობასა და ამ მუხტის სიდიდეზე.
ანალოგიური თვისება აქვს გრავიტაციულ ველსაც და ამაში არაფერია გასაკვირი, რადგანაც გრავიტაციული და კულონური ძალები მსგავსი ფორმულით აღიწერება.
მუშაობის ტრაექტორიის ფორმისაგან დამოუკიდებლობის შედეგია შემდეგი მტკიცება:
ელექტროსტატიკური ველის ძალების მუშაობა მუხტის ნებისმიერ ჩაკეტილ ტრაექტორიაზე გადაადგილებისას ნულის ტოლია.
ძალურ ველებს, რომლებსაც ეს თვისება აქვთ, პოტენციურ ან კონსერვატორულს უწოდებენ.
ნახ. 2-ზე გამოსახულია Q წერტილოვანი მუხტის კულონური ველის ძალწირები და საცდელი q მუხტის საწყისი (1) წერტილიდან საბოლოო (2) წერტილში გადაადგილების ორი განსხვავებული ტრაექტორია. ერთერთ ტრაექტორიაზე გამოყოფილია მცირე გადაადგილება \(\Delta\vec{l}\). ამ გადაადგილებაზე კულონური ძალების მუშაობა ΔA ტოლია
\(\Delta A=F\Delta l\cos\alpha=Eq\Delta r=\frac{1}{4\pi\varepsilon_{0}}\frac{Qq}{r^{2}}\Delta r.\)
ამგვარად, მუშაობა მცირე გადაადგილებაზე დამოკიდებულია მუხტებს შორის r მანძილსა და მის Δr ცვლილებაზე. თუ ამ გამოსახულებას r = r1-დან r = r2-მდე ინტერვალში გავაინტეგრალებთ, მივიღებთ
\(A=\int_{r_{1}}^{r_{2}}E\cdot q\cdot dr=\frac{Qq}{4\pi\varepsilon_{0}}\left (\frac{1}{r_{1}}-\frac{1}{r_{2}} \right ).\)
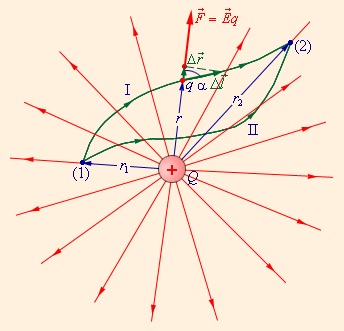
ნახ. 2.
q მუხტის გადაადგილებისას კულონური ძალების მუშაობა დამოკიდებულია მხოლოდ ტრაექტორიის საწყის და საბოლოო წერტილებამდე r1 და r2 მანძილებზე
მიღებული შედეგი არ არის დამოკიდებული ტრაექტორიის ფორმაზე. ნახ. 2- ზე I და II ტრაექტორიებზე კულონური ძალების მუშაობა ერთნაირია. თუ ერთ-ერთ ტრაექტორიაზე საცდელი q მუხტის გადაადგილების მიმართულებას შევცვლით, მუშაობა ნიშანს შეიცვლის. აქედან გამომდინარეობს, რომ ჩაკეტილ ტრაექტორიაზე კულონური ძალების მუშაობა ნულის ტოლია.
თუ ელექტროსტატიკური ველი შექმნილია \(Q_{i}\) წერტილოვანი მუხტების ერთობლიობით, მაშინ საცდელი q მუხტის გადაადგილებისას ჯამური ველის A მუშაობა, სუპერპოზიციის პრინციპის თანახმად, წერტილოვანი მუხტების კულონური \(A_{i}\) ველების აჯამვით მიიღება: \(A=\sum A_{i}\). რადგანაც ჯამის არცერთი წევრი \(A_{i}\) ტრაექტორიის ფორმაზე დამოკიდებული არ არის, არც ჯამური ველის A მუშაობაა ტარექტორიაზე დამოკუდებული, არამედ დამოკიდებულია მხოლოდ საწყისი და საბოლოო წერტილების მდებარეობაზე.
ელექტროსტატიკური ველის პოტენციურობის თვისება მუხტის პოტენციური ენერგიის ცნების შემოტანის საშუალებას იძლევა. ამისათვის სივრცეში უნდა აირჩეს რაღაც (0) წერტილი და ამ წერტილში მოთავსებული q მუხტის პოტენციური ენერგია უნდა ჩაითვალოს ნულის ტოლად.
სივრცის ნებისმიერ (1) წერტილში მოთვსებული q მუხტის პოტენციური ენერგია ფიქსირებული (0) წერტილის მიმართ იმ A10 მუშაობის ტოლია, რომელსაც ელექტროსტატიკური ველი ასრულებს მუხტის (1) წერტილიდან (0) წერტილში გადასაადგილებლად:
Wp1 = A10.
(ელექტროსტატიკაში ენერგიას აღნიშნავენ W ასოთი, რადგანაც E ასოთი დაძაბულობის აღნიშვნაა მიღებული.)
მექანიკის მსგავსად, პოტენციური ენერგია განისაზღვრება მუდმივი სიდიდის სიზუსტით, რომელიც საყრდენი (0) წერტილის შერჩევაზეა დამოკიდებული. პოტენციური ენერგიის ასეთი არაცალსახა განსაზღვრა გარკვეულ გაუგებრობებს იწვევს, რადგან ფიზიკური აზრი აქვს არა თვით პოტენციურ ენერგიას არამედ ორ წერტილს შორის მისი მნიშვნელობების სხვაობას.
წერტილოვანი q მუხტის (1) წერტილიდან (2) წერტილში გადაადგილებისას ელექტროსტატიკური ველის მიერ შესრულებული მუშაობა ტოლია ამ წერტილებში პოტენციური ენერგიების სხვაობისა და არარის დამოკიდებული გადაადგილების ტრაექტორიასა და (0) წერტილის არჩევაზე.
A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2.
ელექტროსტსტიკურ ველში მოთავსებული q მუხტის პოტენციური ენერგია ამ მუხტის სიდიდის პროპორციულია.
ფიზიკური სიდიდე, რომელიც ტოლია ელექტროსტატიკურ ველში ელექტრული მუხტის პოტენციური ენერგიის ფარდობისა ამ მუხტის სიდიდესთან, ელექტრული ველის პოტენციალს უწოდებენ:
\(\varphi=\frac{W_{p}}{q}.\)
პოტენციალი φ ელექტროსტატიკური ველის ენერგეტიკულ მახასიათებელს წარმოადგენს.
ელექტრული q მუხტის საწყისი (1) წერტილიდან საბოლოო (2) წერტილში გადაადგილების A12 მუშაობა ტოლია მუხტის სიდიდის ნამრავლისა საწყისის და საბოლოო წერტილების პოტენციალთა სხვაობაზე (φ1 – φ2):
A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2).
საერთაშორისო სი სისტემაში პოტენციალის ერთეულია ვოლტი (ვ).
1 ვ = 1 ჯ / 1 კ.
ელექტროსატატიკის ბევრ ამოცანაში პოტენციალის გამოთვლისას ხელსაყრელია საყრდენ წერტილად უსასრულოდ დაშორებული წერტილის აღება. ასეთ შემთხვევაში პოტენციალის ცნება შეიძლება შემდეგნაირად ჩამოყალიბდეს:
სივრცის მოცემულ წერტილში ველის პოტენციალი ტოლია იმ მუშაობისა, რომელსაც ასრულებენ ელექტრული ძალები ერთეულოვანი დადებითი მუხტის მოცემული წერტილიდან უსასრულობაში გადასაადგილებლად.
\(\varphi_{\infty}=\frac{A_{\infty}}{q}.\)
წერტილოვანი Q მუხტის ველის φ∞ პოტენციალი მისგან r მანძილზე უსასრულოდ დაშორებული წერტილის მიმართ შემდეგნაირად გამოითვლება:
\(\varphi=\varphi_{\infty}=\frac{1}{q}\int_{r}^{\infty}Edr=\frac{Q}{4\pi\varepsilon_{0}}\int_{r}^{\infty}\frac{dr}{r^{2}}=\frac{1}{4\pi\varepsilon_{0}}\frac{Q}{r}.\)
გაუსის თეორემიდან გამომდინარე, ეს ფორმულა გამოსახავს ერთგვაროვნად დამუხტული ბურთულის (ან სფეროს) ველის პოტენციალს, როცა r ≥ R, სადაც R - ბურთულის რადიუსია.
ელექტროსტატიკური ველის თვალნათლივ წარმოდგენისათვის ძალწირების გვერდით ექვიპოტენციალური ზედაპირები გამოიყენება.
ზედაპირი, რომლის ყოველ წერტილში ელექტრული ველის პოტენციალს ერთნაირი მნიშვნელობა აქვს ექვიპოტენციური ზედაპირი ან ტოლი პოტენციალების ზედაპირი ეწოდება.
ელექტროსტატიკური ველის ძალწირები ყოველთვის ექვიპოტენციური ზედაპირების მართობულია.
წერტილოვანი მუხტის კულონური ველის ექვიპოტენციური ზედაპირები - კონცენტრული სფეროებია. ნახ. 3-ზე ზოგიერთი უბრალო ელექტრული ველების ექვიპოტენციური ზედაპირები და ძალწირებია წარმოდგენილი.
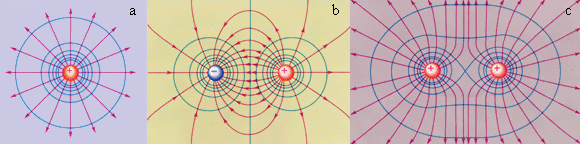
ნახ. 3.
უბრალო ელექტრული მუხტების ექვიპოტენციური ზედაპირები (ლურჯი ხაზები) და ძალწირები (წითელი ხაზები): a - წერტილოვანი მუხტი; b - ელექტრული დიპოლი: c - ორი ტოლი დადებითი მუხტი
ერთგვაროვანი ველის შემთხვევაში ექვივალენტური ზედაპირები პარალელური სიბრტყეების სისიტემას წარმოადგენს.
თუ საცდელმა q მუხტმა შეასრულა ძალწირის გასწვრივ მცირე \(\Delta\vec{l}\) გადაადგილება (1) წერტილიდან (2) წერტილში, შეიძლება ჩავწეროთ:
ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ,
სადაც Δφ = φ1 – φ2 – პოტენციალი ცვლილებაა. აქედან გამოდის
\(E=-\frac{\Delta\varphi}{\Delta l};\: (\Delta l\to 0)\) ან \(E=-\frac{d\varphi}{dl}.\)
ეს ფორმულა ველის დაძაბულობასა და პოტენციალს შორის კავშირს სკალარულად გამოსახავს. აქ l - ძალწირის გასწვრივ ათვლილი ძალწირის კოორდინატაა.
ელექტრული მუხტების ველების დაძაბულობების სუპერპოზიციის პრინციპიდან გამომდინარეობს პოტენციალების სუპერპოზოციის პრინციპი:
φ = φ1 + φ2 + φ3 + ...


