• ბიო-სავარის კანონი. ცირკულაციის თეორემა
• მაგნიტური ველი ნივთიერაბაში

B მაგნიტურ ველში მდებარე \(\Delta l\)  სიგრძის გამტარზე, რომელშიც \(I\) ძალის დენი გადის, მომქმედი ამპერის ძალა

\(F=IB\Delta l\sin \alpha\)

შეიძლება გამოისახოს ისეთი ძალების საშუალებით, რომლების მუხტის ცალკეულ მატარებლებზძე მოქმედებენ.

ვთქვათ გამტარში თავისუფალი მუხტის მატარებლების კონცენტრაცია n-ია, ხოლო q – მატარებლის მუხტია. მაშინ ნამრავლი \(qnvS\) , სადაც \(v\) – გამტარში მატარებლების მოწესრიგებული მოძრაობის სიჩქარის სიდიდეა, ხოლო S – გამტარის განიკვეთის ფართობია,  გამტარში გამავალი დენის ტოლია:

\(I=qnvS\).

ამპერის ძალის გამოსახულება შეიძლება ასე ჩაიწეროს:

 \(F=qnS\Delta lvB\sin \alpha\).

რადგანაც \(\Delta l\)  სიგრძის და S  განივკვეთის გამტარში თავისუფალი მუხტის მატარებლების სრული რიცხვი N ტოლია \(nS\Delta l\), ამიტომ ერთ დამუხტულ ნაწილაკზე მომქმედი ძალა ტოლია

\(F\)_ლ\(=qvB\sin \alpha\).

 ამ ძალას ლორენცის ძალას უწიდებენ.  ამ გამოსახულებაში \(\alpha\) კუთხე  \(\vec{v}\) სიჩქარესა და \(\vec{B}\) მაგნიტული ინდუქციის ვექტორს შორის კუთხის ტოლია. დადებითად დამუხტულ ნაწილაკზე მომქმედი ლორენცის ძალის მიმართულება, ამპერის ძალის მიმართულების მსგავსად შეიძლება მარცხენა ხელის ან ბურღის წესის საშუალებით დადგინდეს. \(\vec{F}\)_ლ, \(\vec{B}\) და  \(\vec{v}\) ვექრორების ურთიერთ განლაგება დადებითად დამუხტული ნაწილაკისთვის ნახ. 1-ზეა ნაჩვენები.

   

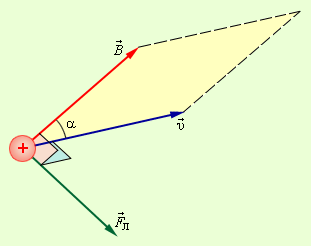
ნახ. 1.

\(\vec{F}\)_ლ, \(\vec{B}\) და  \(\vec{v}\)  ვექრორების ურთიერთ განლაგება. ლორენცის \(\vec{F}\)_ლ ძალა რიცხობრივად  \(\vec{v}\) და \(\vec{B}\) ვექტორებზე აგებული პარალელოგრამის ფართობის q მუხტზე ნამრავლის ტოლია

ლორენცის ძალა   \(\vec{v}\) და \(\vec{B}\) ვექტორების მართობულია. დამუხტული ნაწილაკის მაგნიტურ ველში მოძრაობისას ლორენცის ძალა მუშაობას არ ასრულებს. ამიტომ ნაწილაკის მოძრაობისას  ნაწილაკის სიჩქარის სიდიდე არ იცვლება.

თუ დამუხტული ნაწილაკი ლორემცის ძალის მოქმედებით ერთგვაროვან მაგნიტურ ველში მოძრაობს, ხოლო მისი \(\vec{v}\) სიჩქარე \(\vec{B}\) ვექტორის მართობულ სიბრტყეში მდებარეობს, მაშინ ნაწილაკები იმოძრავებენ წრეწირზე, რომლის რადიუსია

 \(R=\frac{mv}{qB}\)

ამ შემთხვევაში ლორენცის ძალა ცენტრისკენული ძალის როლს ასრულებს (ნახ. 2).

 

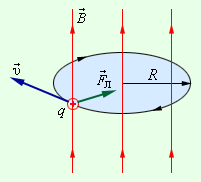
ნახ. 2.

დამუხტული ნაწილაკის წრიული მოძრაობა ერთგავროვან მაგნიტურ ველში

ერთგავროვან მაგნიტურ ველში ნაწილაკის ბრუნვის პერიოდი ტოლია

 \(T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\).

ეს გამოსახულება უჩვენებს, რომ მოცემული მასის დამუხტული ნაწილაკების ბრუნვის პერიოდე არ არის დამოკიდრბული \(v\) სიჩქარესა და ტრაექტორიის R რადიუსზე.

წრიულ ტრაექტორიაზე დამუხტული ნაწილაკების მოძრაობის კუთხურ სიჩქარეს

 \(\omega =\frac{v}{R}=v\frac{qB}{mv}=\frac{qB}{m}\)

ციკლოტრონულ სიჩქარეს უწოდებენ. ციკლოტრონული სიჩქარე არ არის დამოკიდებული ნაწილაკის სიჩქარეზე (და ე.ი. არც კინეტიკურ ენერგიაზე). ეს გარემოება გამოიყენება ციკლოტრონებში - მძიმე ნაწილაკების ( პროტონების, იონების) ამაჩქარებლებში. ციკლოტრონის პრინციპული სქემა ნახ. 3-ზეა მოყვანილი.

ნახ. 3.

გამუხტული ნაწილაკის მოძრაობა ციკლოტრონის ვაკუუმურ კამერაში

ძლიერი ელექტრომაგნიტის პოლუსებს შორის ვაკუუმური კამერა თავსდება, რომელშიც ორი ღრუ ნახევარცილინდრის ფორმის მეტალური ელექტროდია მოთავსებული (დუანტები). დუანტებზე ცვალდი ელექტრული ძაბვაა მოდებული, რომლის სიხშირეც ციკლოტრონული სიხშირის ტოლია. დამუხტული ნაწილაკები შეჰყავთ ვაკუუმური კამერის ცენტრში. ნაწილაკები დუანტებსშორისი ელექტრული ველის მოქმედებით აჩქარდებიან. დუანტებს შიგნით ნაწილაკები ლორენცის ძალის მოქმედებით ნახევარ წრეებზე მოძრაობენ, რომელთა რადიუსები ნაწილაკების ენერგიის ზრდასთან ერთად იზრდებია. ყოველთვის, როცა ნაწილაკი ჩაიფრენს დუანტებს შორის ნაპრალში (ღრეჭოში) ის ელექტრული ველის გავლენით ჩქარდება. ამგვარად, ციკლოტრონში, ისევე როგორც ყველა სხვა ამაჩქარებელში, დამუხტული ნაწილაკი ელექტრული ველის მოქმედებით ჩქარდება, ხოლო ტრაექტორიაზე მაგნიტური ველის გავლენით კავდება. ციკლოტრონები პროტონების 20 მეგავოლტამდე აჩქარების საშუალებას იძლევიან.

ერთგვაროვანი მაგნიტური ველი მრავალ ხელსაწყოში  და, კერძოდ, მას-სპექტრომეტრებში გამოიყენება. მას-სპექტრომეტრები ხელსაწყოებია, რომელთა საშუალებით დამუტული ნაწილაკების - იონებისან სხვადასხვა ნივთიერების ატომის ბირთვების - მასის გაზომვაა შესაძლებელი. მას-სპექტრომეტრების გამოიყენება იზოტოპების,  ე.ი.ერთნაერი მუხტის, მაგრამ სხვადსხვა მასის ატომების (მაგალითად,²⁰Ne და ²²Ne) გასაყოფად. უმარტივესი მას-სპექტრომეტრი ნახ. 4-ზეა ნაჩვენები. S წყაროდან გამოფრენილი იონები, რამოდენიმე პატარა ხვრელში შედიან  და ქმნიან ვიწრო ნაკადს. შემდეგ ისინი სიჩქარეების სელექტორში ხვდებიან, რომელშიც ნაწილაკები მოძრაობენ ურთიერთგადამკვეთ ელექტრულ და მაგნიტურ ველებში. ელექტრული ველი ბრტყელი კონდენსატორის ფირფიტებს შორის იქმნება, მაგნიტური ველი კი, ელექტრომაგნიტის პოლუსებს შორის ღრეჭოში. დამუხტული ნაწილაკის საწყისი \(\vec{v}\) სიჩქარე \(\vec{E}\) და \(\vec{B}\) ვექტორების მართობულია. ურთიერთგადამკვეთ ელექტრულ და მაგნიტურ ველებში მოძრავ ნაწილაკზე მოქმედებს ელექტრული ძალა \(q\vec{E}\) და ლორენცის მაგნიტური ძალა. თუ \(E=vB\)  ეს ძალები ზუსტად აწონასწორებენ ერთმანეთს. თუ ეს პირობა სრულდება, ნაწილაკი თანაბრად და წრფივად იმოძრავებს და, გაიფრენს რა კონდენსატორში, გაივლის ეკრანის ხვრელში. ელექტრული და მაგნიტური ველების გარკვეული მნიშვნელობებისათვის სელექტორი \(v=\frac{E}{B}\) სიჩქარით მოძრავ  ნაწილაკებს გამოჰყოფს.

ამის შემდეგ ერთნაერი სიჩქარეების მქონე ნაწილაკები ხვდებიან მას-სპექტრომეტრის კამერაში, სადაც შექმნილია ერთგვაროვანი \(\vec{B}'\) მაგნიტური ველი.  კამერაში ნაწილაკები, ლორენცის ძალის მოქმედებით, მაგნიტური ველის მართობულ სიბრტყეში მოძრობენ. ნაწილაკების ტრაექტორიები \(R=\frac{mv}{q{B}'}\)წრეწორებს წარმოადგენენ. ცნობილი \(v\) და B' სიდიდეების შემთხვევაში ტრაექტორიის რადიუსების გაზომვით შეიძლება q / m ფარდობის განსაზრვრა. იზოტოპების შემთხვევაში (q₁ = q₂) მას-სპექტრომეტრი სხვადასხვა მასების მქონე მაწოლაკების გაყოფის საშუალებას იძლევა.

თანამედროვე მას-სპექტრომეტრები საშუალებას იძლევიან დამუხტული ნაწილაკის მასა გაიზომის 10^–4-ზე მეტი სიზუსტით.

 ნახ. 4.

სიჩქარეების სელექტორი და მას-სპექტრომეტრი

თუ ნაწილაკის \(\vec{v}\) სიჩქარეს აქვს \(\vec{v}_{\parallel}\) მაგნიტური ველის გასწვრივი მდგენელი, მაშინ ასეთი ნაწილაკი ერთგვაროვან მაგნიტურ ველში სპირალზე იმოძრავებს. ამ დროს სპირალის R რადიუსი დამოკიდებულია \(\vec{v}\) ვექტორის მაგნიტური ველის მართობული \(v_{\perp }\) მდგენელის სიდიდეზე, ხოლო სპირალის ბიჯი p - გასწვრივი  \(v_{\parallel}\)  მდგენელის სიდიდიზე (ნახ. 5).

 

ნახ. 5.

დამუხტული ნაწილაკის მოძრაობა ერთგვაროვან სპირალურ მეგნიტირ ველში

ამგვარად, დამუხტული ნაწილაკის ტრაექტორია თითქოს მაგნიტური ინდუქციის წირს ემთხვევა. ეს მოვლენა ტექნიკაში გამოიყენება მაღალტემპერატურული პლაზმის -ანუ 10⁶ K რიგის ტემპერატურაზე მთლიანად იონიზირებული გაზის - მაგნიტური იზოლაციის მიზნით. ნივთიერება ასეთ მდგომარეობაში მიიღება „ტოკომაკის“ ტიპის დანადგარებში თერმობირთვული რეაქციების შესწავლის დროს. პლაზმა არ უნდა ეხებოდეს კამერის კედლებს. თერმოიზოლაცია მიიღწევა სპეციალური კონფიგურაციის მაგნიტური ველის შექმნით. მაგალითისათვის ნახ. 6-ზე გამოსახულია დამუხტული ნაწილაკის მოძრაობა მაგნიტურ „ბოთლში“ (ან სათაგურში).

 

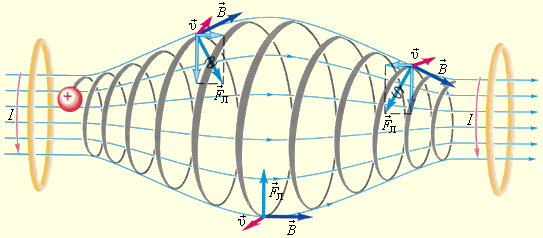
ნახ. 6.

მაგნიტური „ბოთლი“. დამუხტული ნაწილაკები „ბოთლის“ საზღვრებიდან არ გამოდიან. „ბოთლის“ მაგნიტური ველი შეიძლება ორი მრგვალი დენიანი კოჭას საშუალებით შეიქმნას

ანალოგიური მოვლენა ხდება დედამიწის მაგნიტურ ველში, რომელიც ყოველივე ცოცხალის დამცველია კოსმოსური სივრციდან მომავალი დამუხტული ნაწილაკების ნაკადებისაგან. დედამიწის მაგნიტური ველი „ჩაიჭერს“ კოსმოსიდან (ძირითადად მზიდან) მომავალ სწრაფ დამუხტილ ნაწილაკებს და ქმნის ე.წ. რადაიციულ სარტყელს (ნახ. 7), რომელშიც ნაწილაკი, როგორც მაგნიტურ სათაგურში  აქეთ-იქით მოძრაობს სპირალის მსგავს ტრაექტორიებზე ჩრდილოეთ და სამხრეთ პოლუსებს შორის წამის ნაწილების რიგის დროის პერიდით. მხოლიდ პოლარულ არეებში ნაწილაკების რაღაც ნაწილი აღწევს ატმოსფეროს ზედა ფენაბში და ჩრდილოეთის ციალს იწვევს. დედამიწის რადიაციული სარტყელი 500კმ-დან ათობით დედამიწის რადიუსამდე მანძილზე ვრცელდება. უნდა გვახსოვდეს, რომ დედამიწის სამხრეთ მაგნიტური პოლუსი მდებარეობს ჩრდილოეთ გეოგრაფიული პოლუსის მახლობლად (გრენლანდიის ჩრდილო დასავლეთით). დედამიწის მაგნეტიზმის ბუნება ჯერკიდევ არ არის შესწავლილი.

  

ნახ. 7.

დედამიწის რადიაციული სარტყელი. მზიდან მომავალი სწრაფი დამუხტული ნაწილაკები (ძირითადად ელექტრონები და პროტონები) რადიაციული სარტყლის მაგნიტურ სათაგურში ხვდებიან. ნაწილაკებს შეუძლიათ დატოვონ სარტყელი პოლუსების არეებში და შეიჭრნენ ზედა ატმოსფერულ ფენებში და  ჩრდილოეთის ციალი გამოიწვიონ