{loadnavigation}
პრაქტიკაში განსაკუთრებით საინტერესოა სინათლის დიფრაქციის შემთხვევა, როცა წინააღმდეგობა ღიად ფრენელის პირველი ზონის მხოლოდ მცირე ნაწილს ტოვებს. ამ შემთხვევას ადგილი აქვს თუ სრულდება პირობები

ანუ ამ შემთხვევაში დიფრაქციული სურათი მცირე ზომის წინააღმდეგობიდან ძალიან დიდი მანძილზე უნდა დაიკვირვებოდეს. მაგალითად, თუ R = 1 მმ, λ = 550 ნმ (მწვანე სინათლე), მაშინ დაკვირვების სიბრტყემდე L მანძილი 2 მ-ს მნიშვნელოვნად უნდა აღემატებოდეს (ე.ი. მინიმუმ 10მ ან მეტი). ტალღის ფრონტის სხვადასხვა ელემენტებიდან დაკვირვების შორეულ წერტილამდე გავლებული სხივები შეიძლება პარალელურად ჩაითვალოს. დიფრაქციის ამ შემთხვევას სწორად ასე უწოდებენ - პარალელური სხივების დიფრაქცია ან ფრაუნჰოფერის დიფრაქცია - გერმანელი ფიზიკოსის ი.ფრაუნჰოფერის საპატივცემლოდ, რომელიც ფრენელის თანამედროვე იყო. თუ სხივების გზაზე წინააღმდეგობის შემდეგ შემკრებ ლინზას მოვათავსებთ, პარალელურ სხივთა კონა, რომელმაც დიფრაქცია განიცადა წინააღმდეგობაზე, რაღაც θ კუთხით თავს მოიყრის ფოკალური სიბრტყის რაღაც წერტილში (ნახ. 1). აედან გამომდინარე, ლინზის ფოკალური სიბრტყის ნებისმიერი წერტილი ექვივალენტურია ლინზის გარეშე უასასრულოდ დაშორებული წერტილისა.
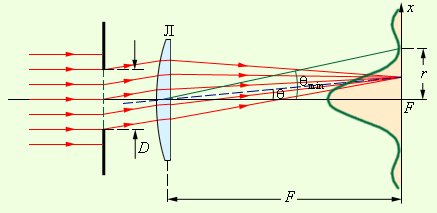
ნახ. 1.
პარალელური სხივების დიფრაქცია. მწვანე მრუდი -ინტენსივობების განაწილება ფოკალურ სიბრტყეში (ღერძის მასშტაბი ძალიან გაზრდილია)
ლინზის ფოკალურ სიბრტყეში ფრაუნჰოფერის დიფრაქციული სურათი დაიკვირვება. მაგრამ, გეომეტრული ოპტიკის თანახმად, ლინზის ფოკუსში შორეული საგნის წერტილოვანი გამოსახულენა უნდა მიიღებოდეს. მაგრამ სინამდვილში წერტილოვანი საგნის გამოსახულება დიფრაქციის გამო იდღაბნება. ამაში ვლინდება სინათლის ტალღური ბუნება.
არანაირ ოპტიკურ სისტემას წერტილოვანი გამოსახულების მოცემა არ შეუძლია. ფრაუნჰოფერის დიფრაქციის შემთხვევაში D დიამეტრის მრგვალ ხვრელზე დიფრაქციული გამოსახულება შედგება მხოლოდ ცენტრალური ნათელი ლაქისგან (ეირის დისკი), რომელზეც სინათლის ენერგიის თითქმის 85% მოდის, და მისი გარემომცველი ნათელი და ბნელი ზოლებისაგან (ნახ. 2). სწორედ ეს დიფრაქციული ლაქა ითვლება წერტილოვანი წყაროს გამოსახულებად. ცენტრალური ლაქის რადიუსი ლინზის ფოკალურ სიბრტყეზე ტოლია
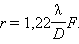
თუ დაშორებილი წყაროდან სინათლის სხივი ეცემა პირდაპირ ლინზას, მაშინ იმ ეკრანის როლს, რომელზედას სინათლე განიცდის დიფრაქციას, ლინზის ჩარჩო ასრულებს. ამ შემთხვევაში D -ში ლინზის დიამეტრი იგულისხმება.

ნახ.2.
წერტილოვანი წყაროს დიფრაქციული გამოსახულება (დიფრაქცია მრგვალ ხვრელზე). ცენტრალურ ლაქაზე სინათლის ენერგიის თითქმის 85% მოდის
დიფრაქციული გამოსახულების ზომა ძალიან მცირეა. მაგალითად, D = 5 სმ დიამეტრისა და F = 50 სმ ფოკუსური მანძილის მქონე ლინზის λ = 500 ნმ ტალღის სიგრძის მონოქრომატული სინათლისთვის ფოკალურ სიბრტყეში ცენტრალური ნათელი ლაქის რადიუსი 0,006 მმ-ს ტოლია. ბევრ ოპტიკურ მოწყობილობაში (ფოტოაპარატი, პროექტორი და სხვა) გამოსახულების დიფრაქციული გადღაბნა ინიღბება ოპტიკის არასრულყოფილებით გამოწვეული გაცილებით უფრო ძლიერი დამახინჯებით.
მაგრამ მაღალი ხარისხის ასტრონომიულ ხელსაწყოებში გამოსახულიბის ხარისხის დიფრაქციული ზღვარი ხორციელდება. ობიექტის ორი ახლომდებარე წერტილის გამოსახულება დიფრაქციული გადღაბნის შედეგად შეიძლება ვერ გაირჩეს ერთი წერტილისაგან (ერთმანეთისაგან). მაგალითის სახით განვიხილოთ შემთხვევა, როცა ასტრონომიული ტელესკოპის ობიექტივი მიმართულია ორი ახლომდებარე ვარსკვალვისაკენ, ერთმანეთისაგან ψ კუთხურ მანძილზე. იგულისხმება, რომ ყველა დეფექტი და აბერაცია მოშორებულია, და ობიექტივის ფოკალურ სიბრტყეში დაიკვირვება ვარსკვლავების დიფრაქციული გამოსახულება (ნახ. 3).

ნახ. 3.
ორი ახლომდებარე ვარსკვლავის დიფრაქციული გამოსახულება ტელესკოპოს ობიექტივის ფოკალურ სიბრტყეში
ნახ. 3-ზე ვარსკვლავების დიფრაქციულ გამოსახულებათა ცენტრებს შორის Δl მანძილი აჭარბებს ცენტრალუტი ნათელი ლაქის r რადიუსს - ამ შემთხვევაში ვარსკვალვების გამოსახულებები დამკვირვებლის მიერ ცალ-ცალკე აღიქმება და, ე.ი. ტელესკოპის ობიექტივი ორი ახლომდებარე ვაესკვალავის გარჩევის საშუალებას იძლევა. ვარსკვლავებს შორის ψ კუთხური გარჩევის შემცირების შემთხვევაში დიფრაქციოლ გამოსახულებებს შეუძლიათ ძლიერად გადაფარონ ერთმანეთი და არ განირჩევიან ერთი ვარსკვლავის გამოსახილებისაგან. ამ შემთხვევაში ტელესკოპის ობიექტივი ვერ არჩევს ახლომდებარე ვარსკვლავებს. XIX საუკუნის ბოლოს ინგლისელმა ფიზიკოსმა რელეიმ წამოაყენა პირობა, რომ გარჩევა ჩაითვალოს სრულად, თუ გამოსახულების ცენტრებს შორის Δl მანძილი ტოლია (ან აჭარბებს) ეირის დისკის r რადიუსს (ნახ. 3.9.4). პირობას Δl = r გარჩევის რელეის კრიტერიუმს უწოდებენ. ამ კრიტერიუმიდან გამოდის:
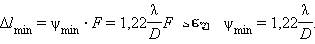
D = 1 მ დიამეტრია ტოლი ობიექტივის მქონე ტელესკოპს შეუძლია გაარჩიოს ორი ვარსკვალავი, რომლების ერთმანეთისაგან ψmin = 6,7·10–7 რად კუთხურ მანძილზე მდებარეობენ (λ = 550 ნმ-სათვის) .
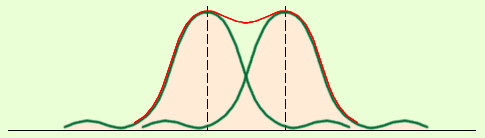
ნახ. 4.
რელეის გარჩევის უნარი. წითელი მრუდი - სინათლის ჯამური ინტენსივობის განაწილება
ორბიტაზე 1990 წელს გაყვანილი ჰაბლის კოსმოსური ტელესკოპის სარკის დიამეტრია D = 2,40 მ. ამ ტელესკოპის ზღვრული კუთხური გარჩევა λ = 550 ნმ ტალღის სიგრძეზე ტოლია: ψmin = 2,8·10–7 რად. ტელესკოპის მუშაობაზე გავლენას არ ახდევს ატმოსფერული შეშფოთებები. ტელესკოპის ობიექტივის დასახასიათებლად შეიძლება ზღვრული კუთხური გარჩევის ψmin შებრუნებული სიდიდის R-ს შემოტანა. ამ სიდიდეს ტელესკოპის გარჩევის უნარს უწოდებენ:

ტელესკოპის გარჩევის უნარის გასაზრდელად უნდა გაიზარდოს ობიექტივის დიამეტრი (ან გამოყენებული უნდა იქნეს უფრო მოკლე ტალღები). ყველაფერი რაც ზემოთ ითქვა ტელესკოპისათვის შეუიარაღებელი თვალისათვისაც სამართლიანია. დაშორებული საგნის დათვალიერებისას თვალი ისევე მოქმედებს როგორც ტელესკოპის ობიექტივი. D -ს როლს გუგის დიამეტრი dმზ ასრულებს. ჩავთვალოთ, რომ dმზ = 3 მმ, λ = 550 ნმ და ვიპოვოთ თვალის გარჩევის ზღვრული კუთხე
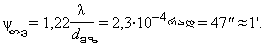
ეს შეფასება კარგ თანხმობაშია თვალის გარჩევის უნარის ფიზიოლოგიურ შეფასებასთან, რომელიც ბადურის სინათლის მგრძნობიარე ელემენტების (ჩხირების და კოლბების) ზომებიდან გამომდინარე მიიღება.
ახლა შეიძლება ერთი საერთო დასკვნის გაკეთება: D დიამეტრისა და λ ტალღის სიგრძის სინათლის კონა სინათლის ტალღური ბუნებიდან გამომდინარე განიცდის დიფრაქციულ გაფართოებას. კონის კუთხური ნახევარსიგანე φ λ / D რიგისაა. ასე რომ, სრული d სიგანე L მანძილზე დაახლოებით ტოლია
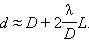
ნახ. 5-ზე ნაჩვენებია, წინააღმდეგობიდან დაშორებით თუ როგორ ტრანსფორმირდება სინათლის კონა.
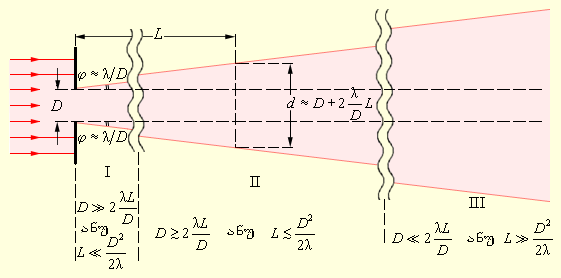
ნახ. 5.
დიფრაქციის გავლენით გაფართოებული სინათლის კონა. I არე – სინათლის სხივის ცნება, გეომეტრული ოპრიკის კანონები. I I არე – ფრენელის ზონები,პუასონოს ლაქა. I I I არე – პარალელური სხივების დიფრაქცია
ნახ. 5-ზე მოყვანილი შეფასებები უჩვენებენ, რომ კონის კუთხური გაშლა მცირდება მისი საწყისი D დიამეტრის ზომის ზრდით. ეს დასკვნა სამართლიანია ნებისმიერი ბუნების ტალღებისთვის. მაგალითად, რომ გავუშვათ ლაზერის გამოსხივების „ვიწრი“ კონა მთვარეზე, ჯერ მისი გაფართოებაა საჭირო. ეს ტელესლოპის საშუალებით მიიღწევა: ლაზერის კონა შედის ოკულარში, გაივლის ტელესკოპის მილს და ობიექტივიდან D დიამეტრის მქონე გამოდის (ნახ. 6).

ნახ. 6.
ლაზერული სხივთა კონის გაფართოება ტელესკოპური სისტემის საშუალებით
ასეთი გაფართოებული კონა მთვარეზე მისვლის მერე, მასზე „გაანათებს“ 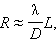 რადიუსის ტოლ ლაქას, სადაც L – მთვარემდე მანძილია. თუ D = 2,5 მ , λ = 550 ნმ, L = 4·106 მ, მაშინ მივიღებთ R ≈ 90 მ. მთვარეზე ლაზერული სინათლის საწყისი კონა რომ გაგვეშვა, რომლის დიამედრია 1სმ, მაშინ მთვარეზე განათებული ფართობი 250-ჯერ დიდი იქნებოდა.
რადიუსის ტოლ ლაქას, სადაც L – მთვარემდე მანძილია. თუ D = 2,5 მ , λ = 550 ნმ, L = 4·106 მ, მაშინ მივიღებთ R ≈ 90 მ. მთვარეზე ლაზერული სინათლის საწყისი კონა რომ გაგვეშვა, რომლის დიამედრია 1სმ, მაშინ მთვარეზე განათებული ფართობი 250-ჯერ დიდი იქნებოდა.
მიკროსკოპის გარჩევის უნარი. მიკროსკოპის საშუალებით ახლომდებარე სხეულები დაიკვირვება, ამიტომ მისი გარჩევის უნარი ხასიათდება არა ორ მახლობელი წერტილს შორის კუთხური, არამედ წრფივი მანძილით, რომლის დროსაც ეს წერტილები კერ კიდევ ცალცალკე დაიკვირვებიან. დასაკვირვებელი ობიექტი ობიექტივის წინა ფოკუსში თავსდება. ხშირად ობიექტივის წინა სივრცე სპეციალური გამჭვირვალე სითხით - იმერსიით - ივსება (ნახ. 7). სიბრტყეში, რომელიც გეომეტრიულად ობიექტთანაა დაკავშირებული, თვალის მიერ ოკულარში დაკვირვებული გადიდებული გამოსახულება თავსდება. ყოველი წერტილის გამოსახულება გადღაბნილია დიფრაქციის შედეგად.
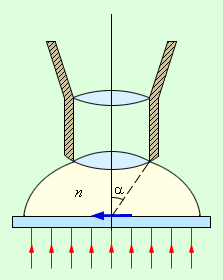
ნახ. 7.
იმერსიული სითხე მიკრისკოპის ობიექტივის წინ
მიკროსკოპის გარჩევის უნარის ზღვარი პირველად გერმანელმა ფიზიკოსმა ჰელმჰოლცმა განსაზღვრა, ჰელჰოლცის ფორმულას აქვს სახე:

სადაც λ – ტალღის სიგრძეა, n – იმერსიული სითხის გარდატეხის კოეფიციენტი, α – ე.წ. აპერურული კუთხე (ნახ. 3.9.7). n sin α სიდიდეს რიცხვითი აპერტურა ეწოდება.
კარ მიკრისკოპებში აპერტურილი კუთხე α მისი ზღვის ტოლია: α ≈ π / 2. როგორც ჰენჰოლცის ფომულიდან ჩანს, იმერსიის გამოყენებით გარჩევის ზღვარი გარკვეულად იზრდება. როცა α ≈ 1, n ≈ 1,5, მივიღებთ:
lmin ≈ 0,4 λ.
ამგვარად, მიკრისკოპის საშუალებით პრინციპულად შეუძლებელია ისეთი დეტალის დათვალიერება, რომლის ზომებიც სინათლის ტალღის სიგრძეზე ნმიშვნელოვნად ნაკლებია. სინათლის ტალღური თვისებები განსაზღვრავენ, ნებისმიერი ოპტიკური სისტემით მიღებული, ობიექტის გამოსახულების ხარისხს.
{loadnavigation}
სინათლის დიფრაქციას წინააღმდეგობის მახლობლად გავლისას სინათლის სხივის წრფივი გავრცელების მიმართულებიდან გადახრის მოვლენას უწოდებენ. როგორ გამოცდილებიდანაა ცნობილი, გარკვეულ პირობებში სინათლეს შეუძლია გეომეტრული ჩრდილის არეში სეშვლა. თუ სინათლის პარალელური კონის გზაზე მრგვალი წინაღობაა მითავსებული (მრგვალი დისკო, ბურთულა ან გაუმჭვივალე ეკრანზე მრგვალი ხვრელი), მაშინ წინააღმდეგობიდან საკმარისად დიდ მანძილზე მოთავსებულ ეკრანზე გამოჩნდება დიფრაქციული სურათი - ნათელი და ბნელი რგოლების მონაცვლეოვა. თუ წინააღმდეგობას წრფივი ხასიათი აქვს (ჭვრიტე, ძაფი, ეკრანის კიდე), მაშინ ეკრანზე გამოჩნდება პარალელური დიფრაქციული ზოლები.
დიფრაქციული მოვლენები ჯერ კიდებ ნიუტონის დროს კარგად იყო ცნობილი, მაგრამ კორპუსკულური თეორიის საფუძველძე მათი ახსნა შეუძლებელი აღმოჩნდა. ამ მოვლენის პირველი თვისობრივი ახსნა ტალღური წარმოდგენების საუძველზე თ.იუნგის მიერ იქნა წარმოდგენილი. მისგან დამოუკიდებლად 1818 წელს ფრანგმა მეცნიერმა ო.ფრენელმა განავითარა დიფრაქციული მოვლევების რაოდენობრივი თეორია. თეორიას საფუძვლად ფრენელმა ჰიუგენსის პრინციპი დაუდო, რომელიც მეორადი ტალღების ინტერფერენციის იდეით შეავსო. ჰიუგენსის პრინციპმა, პირველსაწყისი სახით მხოლოდ ტალღური ფრონტების დროის ყოველ შემდგომი მდებარეობების პოვნის საშუალება მისცა, ე.ი. ტალღის გავრცელების მიმართულების დადგენისა. არსებითად, ეს გეომეტრული ოპტიკის პრინციპია. ჰიუგენსის ჰიპოთეზა, მეორადი ტალღების ფრონტის შესახებ ფრენელმა ფიზიკურად გასაგები პოზიციით შეცვალა, რომლის მიხედვითაც, მეორადი ტალღები დაკვირვების წერტილში გავლისას ერთმანეთთან ინტერფერირებენ. ჰიუგენს-ფრენელის პრინციპი გარკვეულ ჰიპოთეზას წარმოადგენდა, მაგრამ შემდგომმა გამოცდილებამ მისი სამართლიანობა დაადასტურა. ნახ. 1-ზე ჰიუგენს-ფრენელის პრინციპის ილუსტრაციაა მოცემული.

ნახ. 1.
ჰიუგენს-ფრენელის პრინციპი. ΔS1 და ΔS2 – ტალღური ფრონტის ელემენტებია,  и
и 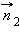 – ნორმალები
– ნორმალები
ვთქვათ S ზედაპირი გარკვეულ მომენტში ტალღის ფრონტს წარმოადგენს. ტალღურ თეორიაში ტალღის ფრონტს უწოდებენ ზედაპირს, რომლის ყოველ წერტილშიც რხევა ფაზის ერთიდაიგივე სიდიდით მიმდინარეობს (სინფაზა). კერძოდ, ბრტყელი ტალღის ტალღის ფრონტი ტალღის გავრცელების მიმართულების მართობულ პარალელურ სიბრტყეთა ოჯახია. წერტილოვანი წყაროს მიერ გამოსხივებული სფერული ტალღის ტალღის ფრონტები კონცენტრულ სფეროთა ოჯახია.
რაიმე P წერტილში ტალღით გამოწვეული რხევა რომ განისაზღვროს, ფრენელის მიხედვით საჭიროა ჯერ განისაზღვროს რხევა გამოწვეული ამ წერტილში გარკვეული მეორადი ტალღებით, რომლებიც ამ წერტილში ყველა ელემენტარული ზედაპირიდან S (ΔS1, ΔS2 და ა.შ.) იყრის თავს, და შემდეგ ეს რხევები უნდა შეიკრიბოს მათი ამპლიტუდებისა და ფაზების გათვალისწინებით. ამასთან, გათვალისწინებული უნდა იყოს მხოლოდ ის ელემენტარული ზედაპირები S, რომლებსაც რაიმე სახის წინაღობა ხვდებათ.
მაგალითისათვის განვიხილოთ უბრალო დიფრაქციული ამოცანა დაშორებული წყაროდან მომავალი ბრტყელი მონოქრომატული ტალღის მიერ გაუმჭვირვალე ეკრანში მცირე R რადიუსის მქონე ხვრელის გავლა (ნახ. 2).
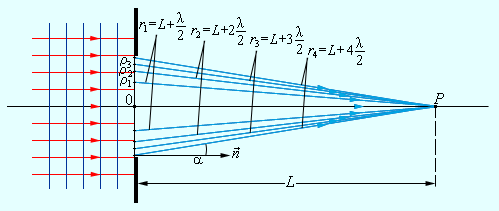
ნახ. 2.
ეკრანში მრგვალი ხვრელის ირგვლივ წარმოქმნილი დიფრაქციული ბრტყელი ტალღები
დაკვირვების P წერტილი სიმეტრიის ღერძზე მდებარეობს ეკრანიდან L მანძილზე. ჰიუგენს-ფრენელის პრინციპის შესაბამისად ტალღური ზედაპირი აზრობრივად ხვრელის სიბრტყესთან თანხვედრილი, მეორადი წყაროებით დასახლებულად უნდა წარმოვიდგინოთ, რომელთაგან ტალღები აღწევენ P წერტილს. მეორადი ტალღების ინტერფერენციის შედეგად P წერტილში გარკვეული ჯამური რხევა წარმოიქმნება, რომლის ამპლიტუდის კვადრატი (ინტენსივობა) უნდა განისაზღვროს დაცემული ტალღის λ ტალღის სიგრძის, A0 ამპლიტუდის წინასწარ მოცემული მნიშვნელობების და ამოცანის გეომეტრიიდან გამომდინარე. გათვლების გასაიოლებლად ფრენელმა წინააღმდეგობის განლაგების ადგილას დაცემული ტალღის ტალღური ზედაპირი დაყო რგოლოვან ზონებად (ფრენელის ზონები) შემდეგი წესით: მეზობელი ზონის საზღვრებიდან P წერტილამდე მანძილი ერთმანეთისაგან ტალღის სიგრძის ნახევრით უნდა განსხვავდებოდნენ, ე.ი.

ტალღის ზედაპირს P წერტილიდან ყურების შემთხვევაში, ფრენელის ზონის საზღვარები კონცენტრულ წრეებს უნდა წარმოადგენდნენ (ნახ. 3).

ნახ. 3.
ხვრელის სიბრტყეში ფრენელის ზონების საზღვრები
ნახ 3-დან ადვილია ფრენელის ზონების ρm რადიუსების პოვნა:

რადგან ოპტიკაში λ << L, ფესვქვეშ მეორე წევრი შეიძლება უგულვებელვყოთ. ფრენელის ზონების რაოდენობა, რომლებიც ხვრელზე თავსდება, მისი R რადიუსით განისაზღვრება:

აქ არ არის აუცილებელი m მთელი რიცხვი იყოს. P წერტილში მეორადი ტალღების ინტერფერენციის შედეგი ფრენელის ღია ზონების m რიცხვბზეა დამოკიდებული. ადვილი საჩვენებელია, რომ ყველა ზონას თანაბარი ფართობი აქვს:
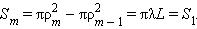
ფართობით ერთნაერი ზონები დაკვირვების წერტილში ერთნაერი ამპლიტუდის რხევებისგან უნდა აღიძვრებოდეს. მაგრამ ყოველი მომდევნო ზონისთვის დაკვირვების წერტილში გავცელებულ სხივსა და ტალღის ზედაპის შორის კუთხე α იზრდება. ფრენელი გამოთქვამდა მოსაზრებას (ექსპერიმენტით განმტკიცებულს), რომ კუთხის გადიდებით რხევის ამპლიტუდა, უმნიშვნელოდ, მაგრამ მაინც მცირდება:
A1 > A2 > A3 > ... > A1
სადაც Am – m-ური ზონით გამოწვეული რხევის ამპლიტუდაა.
კარგ მიახლოებად შეიძლება ჩაითვალოს, რომ ზოგიერთი ზონით გამოწვეული რხევის ამპლიტუდა ორი მეზობელი ზონით გამოწვეული რხევების ამპლიტუდების საშუალო არითმეტიკულის ტოლია, ე.ი.

რადგანაც ორი მეზობელი ზონის დაკვივების წერტილამდე მანძილები ერთმანეთისაგან λ / 2-ით განსხვევდება, ამიტომ, ამ ზონების გამომწვევი რხევები საწინააღმდეგი ფაზებში იმყოფებიან. ამიტომ ორი მეზობელი ზონიდან ტალღა თითქმის აქრობენ ერთმანეთს. დაკვივების წერტილში ჯამური ამპლიტუდა ტოლია
A = A1 – A2 + A3 – A4 + ... = A1 – (A2 – A3) – (A4 – A5) – ... < A1.
ამგვარად, P წერტილში ჯამური რხევის ამპლიტუდა ყოველთვის ნაკლებია რხევის ამპლიტუდაზე, რომელსაც ერთი პირველი ზონა შექმნიდა. კერძოდ, ფრენელის ყველა ზონა რომ ღია იყოს, მაშინ დაკვირვების წერტილში მიაღწევდა წინააღმდეგობით შეუშფოთებელი ტალღა A0 ამპლიტუდით. ამ დროს შეიძლება ჩაიწეროს:
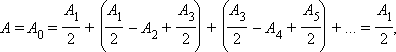
რადგანაც ბრჩხილებში მოთავსებული გამოსახულება ნულის ტოლია. აქედან გამომდინარე, მთელი ტალღური ფრონტის მიერ გამოწვეული მოქმედება (ამპლიტუდა), ერთი ზონის მოქმედების ნახევრის ტოლია.
ამგვარად, თუ გაუმჭვირვალე ეკრანის ხვრელი ღიად ტოვებს ფრენელის მხოლოდ ერთ ზონას, მაშინ დაკვირვების წერტილში რხევის ამპლიტუდა 2-ჯერ იზრდება (ინტენსივობა - 4-ჯერ) აღუშფოთებელ ტალღასთან შედარებით. თუ ღიაა ორი ზონა. რხევის ამპლიტუდა ნულის ტოლი ხდება. თუ არ დავამზადებთ გაუმჭვირვალე ეკრანს, რომელიც ღიად დატოვებს მხოლოდ რამდენიმე კენტ (ან მხოლოს ლუწ) ~ ზონას, მაშინ რხევის ამპლიტუდა გაიზრდება. მაგალითად, თუ ღიაა 1, 3 და 5 ზონები, მაშინ
A = 6A0, I = 36I0
ისეთ ფირფიტებს, რომლებსაც გააჩნიათ სინათლის ფოკუსირების თვისება ზონალურ ფირფიტებს უწოდებენ.
მრგვალ დიკზე სინათლის დიფრაქციისას დახურული არმოჩნდება 1-დან m-მდე ფრენელის ზონა. როცა დაკვირვების წერტილში რხევების ამპლიტუდები ტოლი იქნება
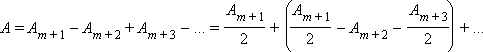
ან A = Am + 1 / 2, რადგანაც, ბრჩხილებში მდგომი გამოსახულება ნულის ტოლია. დისკი ხურავს საკმაოდ დიდი ნომრის მქონე ზონას, მაშინ Am + 1 ≈ 2A0 და A ≈ A0, ე.ი. სურათის ცენტრში სინათლის დიფრაქციისას დისკზე დაიკვირვება ინტერფერენციის მაქსიმუმი. ეს ე. წ. პუასონის ლაქაა, ის ნათელი და ბნელი დიფრაქციული რგოლებითაა გარშემორტყმული.
შევაფასოთ ფრენელის ზონის ზომები. ვთქვათ, მაგალითად, წინააღმდეგობიდან L = 1 მ მანძილზე მოთავსებულ ეკრანზე დაიკვირვება დიფრაქციული სურათი. ტალღის სიგრძე λ = 600 ნმ (წითელი სინათლე). ფრენელის პირველი ზონის რადიუსი ტოლია

ამგვარად, ოპტიკურ დიაპაზონში ტალღის სიგრძეების სიმცირის გამო ფრენელის ზონების ზომები საკმარისად მცერე აღმოჩნდება. დიფრაქციული მოვლენები ყველზე მკაფიოდ ვლინდება, როცა წინააღმდეგობა ზონების მხოლოდ ძალიან მცირე რიცხვს ფარავს:
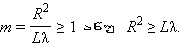
ეს თანაფარდობა შეიძლება განვიხილოთ როგორც დიფრაქციის დაკვირვების კრიტერიუმი. თუ ფრენელის ზონების რიცხვი, რომელსაც წინააღმდეგობა ფარავს, ძალიან დიდი ხდება, დიფრაქციის მოვლენა პრაქტიკულად შეუმჩნეველია:
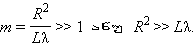
ეს ძლიერი უტოლობა გეომეტრული ოპტიკის გამოყენების საზღვარს განსაზღვრავს. სინათლის ვიწრო კონა, რომელსაც გეომეტრულ ოპტიკაში სხივს უწოდებენ, მხოლოდ ამ პირობების შესრულების შემთხვევაში ფორმირდება. ამგვარად, გეომეტრული ოპტიკა ტალღური ოპტიკის ზღვრულ შემთხვევას წარმოადგენს.
ზევით განხილული იყო დაშორებული წყაროდან მრგვალი ფორმის წინააღმდეგობაზე სინათლის დიფრაქციის შემთხვევა. თუ სინათლის წერტილოვანი წყარო სასრულ მანძილზე მდებარეობას, მაშინ წინააღმდეგობაზე ეცემა სფერულად განშლადი ტალღა. ამ შემთხვევაში ამოცანის გეომეტრია რამდენადმე რთულდება, რამდენადაც ახლა ფრენელის ზონები უნდა აიგოს არა ბრტყელ, არამედ სფერულ ზედაპირზე (ნახ. 4).
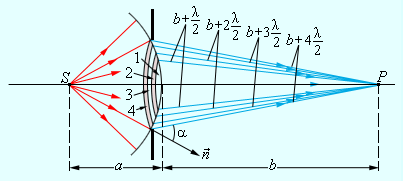
ნახ. 4.
ტალღის სფერული ფრონტის ფრენელის ზონები
ტალღის სფერულ ფრონტზე ფრენელის ზონების ρm რადიუსების გათვლებს შემდეგ გამოსახულებამდე მივყავართ:

ფრენელის თეორიის ზემოთ მოყვანილი დასკვნები ამ შემთხვევაშიც სამართლიანია.
უნდა აღინიშნოს, რომ სინათლის ტალღების დიფრაქციის (და ინტერფერენციის) თეორიის გამოყენება ნებისმიერი ფიზიკური ბუნების ტალღებისთვისაა შესაძლებელი. ამაში ვლინდება ტალღური კანონზომიერებების ერთიანობა. XIX საუკუნის დასაწყისში, როცა იუნგი, ფრენელი და სხვა მეცნიერები ტალღუს თეორიას ქმნიდნენ სინათლის ფიზიკური ბუნება ჯერ კიდევ არ იყო ცნობილი.
{loadnavigation}
ინტერფერენცია სინათლის ტალღური ბუნების ერთ-ერთ აშკარა გამოვლინებაა. ეს საინტერესი და ლამაზი მოვლენა ორი ან რამდენიმე სინათლის კონის ურთიერთზედდების დროს დაიკვირვება. კონების გადაფარვის უბაში სინათლის ინტენსივობა ნათელი და ბნელი ზოლების მიმდევრობით ხასიათდება. ამასთან მაქსიმუმებში ინტენსივობა კონების ჯამურ ინტენსივობაზე მეტია, ხოლო მონიმუმებში ნაკლები. თეთრი სინათლის გამოყენებისას ინტერფერენციული ზოლები სპექტრის სხვადასხვა ფერებადაა შეფერილი. ინტერფერენციულ მოვლენებს საკმაოდ ხშირად ვხვდებით: ასფალტზე ზეთოვანი ლაქების ფერები, ფანჯრის გაყინული მინების შეფერილობა, ლამაზი შეფერილობის ნახატები ზოგიერთი პეპლისა და ხოჭოს ფრთებზე. ყველაფერი ეს ინტერფერევციის გამოვლინებაა.
სინათლის ინტერფერენციის ლაბორატორიულ პირობებში დაკვივების პირველი ექსპერიმენტი ნიუტონს ეკუთვნის. ის აკვირდებოდა ინტერფერენციულ სურათს, რომელიც მინის ბრტყელ ფირფიტასა და დიდი სიმრუდის რადიუსის მქონე ბრტყელ-ამოზნექილ ლინზას შორის თხელ ჰაერის ფენაში სინათლის არეკვლისას წარმოიქმნებოდა (ნახ. 1). ინტერფერენციულ სურათს კონცენტრული რგოლების სახე ჰქონდათ და მათ ნიუტონის რგოლებს უწოდებენ (ნახ. 2).
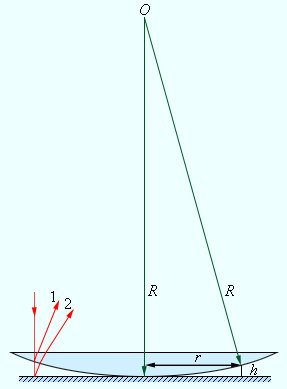
ნახ. 1.
ნიუტონის რგოლების დაკვირვება. ინტერფერენცია წარმოიქმნება ჰაერის ფენის ორი მხრიდან არეკვლილი ტალღების შეკრების შედეგად. სხივი 1 და 2 - ტალღის გავრცელების მიმართულება; h - ჰაერის ფენის სისქე

ნახ. 2.
ნიუტონის რგოლები სინათლის მწვანე და წითელ ფერებში
ნიუტონმა კორპუსკულარული თეორიის თვალსაზრისით ვერ შეძლო აეხსნა, თუ რატომმ წარმოიქმნებიან რგოლები, მაგრამ მას ესმოდა, რომ ეს დაკავშირებული იყო სინათლის რაღაც პერიოდულ პროცესებთან.
პირველი ინტერფერენციული ცდა, რომელიც სინათლის ტალღური ბუნებით აიხსნა იუნგის ცდა იყო (1802 წ.). იუნგის ცდაში სინათლე წყაროდან, რომლის მაგივრიბასაც ვიწრი S ხვრელი ასრულებდა, ეცემოდა ეკრანზე ერთმანეთთან ახლოს განლაგებულ S1 და S2 ხვრელებს (ნახ. 3). თითოეულ ხვრელში გასვლის შემდეგ სინათლის ნაკადი დიფრაქციის გამო ფართოვდებოდა, ამიტომ თეთრ ეკრანზე S1 და S2 ხვრელებიდან გამოსული სინათლის ნაკადები ერთმანეთს ფარავდნენ. გადაფარვის არეში დაიკვირვებოდა ინტერფერენციული სურათი ნათელი და ბნელი ზოლების მონაცვლეობის სახით.
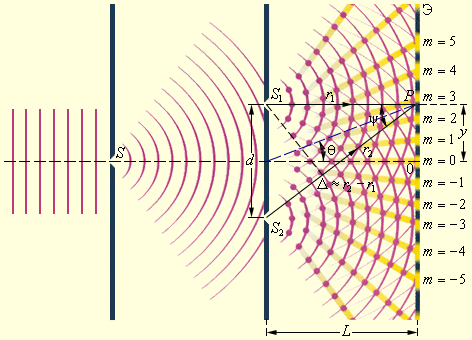
ნახ. 3.
იუნგის ინტერფერენციული ცდის სქემა
იუნგი პირველი მიხვდა, რომ ინტერფერენციის დაკვირვება არ შეიძლება ორი სხვადასხვა დამოუკიდებელი წყაროს ტალღების ზედდების დროს. ამიტომ მის ცდაში S1 და S2 ხვრელები, რომლებიც ჰიუგენსის პრინციპის შესაბამისად შეიძლება განხილულ იყოს, როგორც ერთი S წყაროთი განათებული მეორადი ტალღის წყაროები. მეორადი ტალღის წყაროების სიმეტრიულად განლაგებისას, S1 და S2 ხვრელებიდან გამოსული ტალღები ფაზაში იმყოფებიან, მაგრამ ისნი დაკვირვების P წერტილამდე სხვდასხვა r1 და r2 მანძილებს გადიან. ამიტომ, რხევის ფაზა, რომელსაც S1 და S2 წყაროები P წერტილში ქმნიან, განსხვავებულია. ამგვარად, ამოცანა ტალღების ინტერფერენციის შესახებ ერთიდაიგივე სიხშირის, მაგრამ სხვადასხვა ფაზის მქონე ტალღების შეკრების ამოცანაზე დაიყვანება. მტკიცება იმის შესახებ, რომ S1 და S2 წყაროებიდან ტალღები ვრცელდებიან ერთმანეთისგან დამოუკიდებლად, ხოლო დაკვირვების წერტილში კი უბრალოდ იკრიბებიან, ცდით მიღებული ფაქტია და სუპერპოზიციის სახელს ატარებს.
მონოქრომატული (ან სინუსოიდური) ტალღა, რომელიც 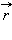 რადიუს-ვექტორის მიმართულებით ვრცელდება, ჩაიწერება შემდეგი სახით
რადიუს-ვექტორის მიმართულებით ვრცელდება, ჩაიწერება შემდეგი სახით
E = a cos (ωt – kr),
სადაც a – ტალღის ამპლიტუდაა, k = 2π / λ – ტალღური რიცხვია, λ – ტალღის სიგრძეა, ω = 2πν – წრიული სიხშირე. ოპტუკურ ამოცანებში ტალღის ელექტრული ველეს E დაძაბულობის ვექტორის სიდიდეა. P წერტილში ორი ტალღის შეკრების შედეგად მიღებული რხევა იგივე ω სიშირეზე ხდება და აქვს რაღაც A ამპლიტუდა და φ ფაზა:
E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).
ხელსაწყოები, რომლებიც სინათილს ტალღის სწრაფ ცვლივებას ადევნებდნენ თვალს, არ არსებობს; დასაკვირვებელ სიდიდე ნაკადის ენერგიაა, რომელიც ტალღის ელექტრული ველის ამპლიტუდის კვადრატის პირდაპირპრიპირციულია. ტალღის ელექტრული ველის ამპლიტუდის კვადრატის ტოლ ფიზიკურ სიდიდეს ინტენსივობას უწოდებენ: I = A2.
იოლი ტრიგონიმეტრიული გარდაქმნები, P წერტილში მიღებული რხევისთვის შემდეგ გამოსახულებას იძლევა:
 (*)
(*)
სადაც Δ = r2 – r1 – ე.წ. სვლათა სხვაობაა.
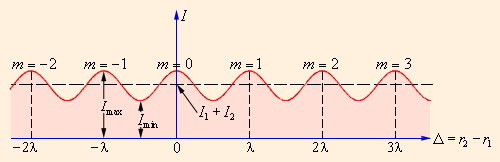
ამ გამოსახულებიდან გამოდის, რომ ინტერფერენციული მაქსიმუმი (ნათელი ზოლი) მიიღწევა სივრცის იმ წერტილებში, სადაც Δ = mλ (m = 0, ±1, ±2, ...). ამასთან Imax = (a1 + a2)2 > I1 + I2. ინტერფერენციული მინიმუმი (ბნელი ზოლი) როცა Δ = mλ + λ / 2. ინტენსივობის მინიმალური მნიშვნრლობა Imin = (a1 – a2)2 < I1 + I2. ნახ. 4-ზე ინტერფერენციულ სურათზე ინტენსივობის განაწილების Δ სვლათა სხვაობაზე დამოკიდებულებაა გამოსახული.
ნახ. 4.
ინტერფერენციულ სურათზე ინტენსივობის განაწილება. m მთელი რიცხი – ინტერფერენციული მაქსიმუმის რიგია
კერძოდ, თუ I1 = I2 = I0, ე.ი. ორივე ტალღის ინტენსივიბა ერთნაერია, (*) გამოსახულება ღებულობს სახეს:
I = 2I0(1 + cos kΔ). (**)
ამ შემთხვევაში Imax = 4I0, Imin = 0.
(*) და (**) ფორმულები უნივერსალური ფორმულები არიან. ისინი ინტერფერენციული სქემისათვისაა სამართლიანი, რომელშიც ორი ერთიდაიგივე სიხშირის მონოქრომატული ტალღის შეკრება ხდება.
თუ იუნგის სქემაში y -ით დაკვირვების წერტილის სიმეტრიის სიბრტყიდან წანაცვლებას ავღნიშნავთ, მაშინ შემთხვევისათვის, როცა d << L и y << L (ოპტიკურ ექსპერიმენტებში ეს პირობები ჩვეულებრივ სრულდება), მიახლოებით შეიძლება მივიღოთ:
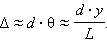
კოორდინატთა y ღერძის გასწვრის, ინტერფერენციული ზოლის სიგანის ტოლ Δl მანძილზე გადაადგილებისას, ე.ი. ერთი ინტერფერენციული მაქსიმუმიდან მეზობელ მაქსიმუმზე გადასვლისას, სვლათა სხვაობა Δ ტალღის ერთი λ სიგრძით იცვლება. აქედან გამომდინარე

სადაც ψ – დაკვირვების P წერტილში „სხივების“ თავმოყრის კუთხეა. შევასრულოთ რაოდენობრივი შეფასებები. დავუშვათ, რომ S1 და S2 ხვრელებს შორის d მანძილი 1 მმ-ს ტოლია, ხოლო ხვრელებიდან Э ეკრანამდე კი L = 1 მ, მაშინ ψ = d / L = 0,001 რად. მწვანე სინათლისათვის (λ = 500 ნმ) მივიღებთ Δl = λ / ψ = 5 · 105 ნმ = 0,5 მმ. წითლისათვის (λ = 600 ნმ) Δl = 0,6 მმ. ასეთი გზით იუნგმა პირველად გაზომა სინათლის ტალღების სიგრძეები, თუმცა ამ გაზომვების სიზუსტე დიდ არ იყო.
ხაზი უნდა გაესვას იმ გარემოებას, რომ ტალღურ ოპტიკაში, გეომეტრული ოპტიკისგან განსხვავებით, სინათლის სხივის ცნება ფიზიკურ აზრს კარგავს. ტერმინი „სხივი“ აქ ტალღის მიმართულების აღნიშვნის გასამარტივებლად გამოიყენება. შემდეგში ამ ტერმინს ბრჭყალების გარეშე გამოვიყენებთ.
ნიუტონის ექსპერიმენტში (ნახ. 1) ტალღოს ლინზის ზედაპირზე ნორნალური (მართობული) დაცემისას სვლათა სხვაობა დაახლოებით ლინზასა და ბრტყელ ფირფიტას შორის ჰაერის გაორმაგებული 2h სისქის ტოლია. იმ შემთხვევისთვის როცა ლინზის სიმრუდის რადიუსი R დიდია h-თან შედარებით, შეიძლება მიახლოებით მივიღოთ:
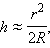
სადაც r – სიმეტრიის ღერძიდან გადახრაა. სვლათა სხვაობის გამოსახულებისათვის, აგრეთვე უნდა გავითვალისწონოთ, რომ 1 და 2 ტალღები სხვადასხვა პირობებში აირეკლებიან. პირველი ტალღა აირეკლება მინა-ჰაერის საზღვრიდან, ხოლო მეორე ჰაერი-მინის საზღვრიდან. მეორე შემთხვევაში ხდება რხევის ფაზის ცვლილება π -თი, რაც ექვივალენტურად ზრდის სვლას λ / 2-ით. ამიტომ:
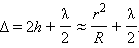
როცა r = 0, ანუ ცენტრში (შეხების წერტილი) Δ = λ / 2; ამიტომ ნიუტონი რგოლის ცენტრში ყოველთვის ინტერფერენციული მინიმუმი დაიკვირვება, ე.ი. ბნელი ზოლი. შემდეგი ბნელი ზოლების rm რადიუსი განისაზღვრება გამოსახულებით
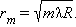
ეს ფორმულა საშუალებას იძლევა ექსპერიმენტულად განისაზღვროს λ ტალღის სიგრძე, თუ ცნიბულია ლინზის სიმრუდის რადიუსი R.
კოჰერენტული ტალღების პრობლემა. იუნგის თეორიის საფუძველზე აიხსნა ორი ერთნაერი სიხშირის მქონე მონოქრომატული ტალღის შეკრებით მიღებული ინტერფერენციული მოვლენა. მაგრამ ყოველდღიური გამოცდილება გვიჩვენებს, რომ სინათლის ინტერფერენციის დაკვირვების სინამდვილეში არც ისე ადვილია. თუ ოთახში ორი ერთნაერი ნათურა ანთია, ოთახის ყოველ წერთილში სინათლის ინტენსივიბები იკრიბება და არავითარი ინტერფერენცია არ დაიკვირვება. ისმის კითხვა, როგორ შემთხვევებში უნდა იკრიბებოდეს დაძაბულობები (ფაზათა თანაფარდობის გათვალისწინებით), როგორი ტალღის ინტენსივობები, ე.ი. დაძაბულობის კვადრატები? მონოქრონატული ტალღების ინტერფერენციის თეორია ამ კითხვაზე პასუხს ვერ იძლევა.
სინათლის რეალური ტალღები მკაცრად მონოქრომატული არ არის. ფუნდამენტური ფიზიკური მიზეზების გამო გამოსხივებას ყოველთვის აქვს სტატისტიკური (ან შემთხვევითი) ხასიათი. სინათლის წყაროს ატომები ერთმანეთისაგან დამოუკიდებლად ასხივებენ დროის შემთხვევით მომენტებში და თითოეული ატომის გამოსხივება ძალის მცირე ხანგრძლიობისაა (τ ≤ 10–8 წმ). წყაროს სრული გამოსხივება ყოველ მომენტში შედგება აურაცხელი ატომების წვლილისგან. τ რიგის დროის შემდეგ ატომების გამოსხივებათა მთელი ერთობლიობა განახლდება. ამიტომაც ჯამურ გამოსხივებას ექნება სხვა ამპლიტუდა და სხვა ფაზა. რეალური დენის წყარის მიერ გამოსხივებული ტალღის ფაზა მიახლოებით უცვლელი რჩება მხოლოდ τ რიგის დროის ინტერვალებში. τ ხანგრძლივობის გამოსხივების ცალკეული „ნაწყვეტებს“ ცუგებს უწოდებენ. ცუგებს cτ-ის ტოლი დროითი სიგრძე აქვტ, სადაც c – სინათლის სიჩქარეა. სხვადასხვა ცუგის რხევა ერთმანეთთან შეთანხმებილი არ არის. ამგვარად, სინათლის რეალური ტალღა, უწესრიგოდ ცვლადი ფაზების მქონე, ტალღური ცუგების მიმდევრობას წარმოადგენს. ამბობენ ხოლმე, რომ სხვადასხვა ცუგების რხევები არაკოჰერენტულია. τ დროის ინტერვალი, რომლის განმავლობაშიაც რხევის ფაზა მიახლოებით უცვლელი რჩება, კოჰერენტულობის დროს უწოდებენ.
ინტერფერენცია შეიძლება წარმოიშვას მხოლოდ კოჰერენტული რხევის შემთხვევაში, ე.ი. რხევისა რომელიც ერთიდაიგივე ცუგას ეკუთვნის. მიუხედავად იმისა, რომ ყოველი ცუგის ფაზა ასევე ექვემდებარება დროში შემთხვევით ცვლილებას, ეს ცვლილებები ერთნაერია, ამიტომაც კოჰერენტული რხევების ფაზათა სხვაობა უცვლელი რჩება. ასეთ შემთხვევაში მდგრადი ინტერფერენციული სურათი დაიკვირვაბა და ე.ი. სრულდება ველების სუპერპოზიციიც პრინციპი. კოჰერენტული რხევების შეკრებისას ფაზათა სხვაობა დროის შემთხვევითი ფუნქციაა. ინტერფერენციული ზოლები განიცდიან აქეთ-იქეთ უწესრუგი გადააგგილებას, და მათი რეგისტრაციის Δt დროის განმავლობაში, რომელიც ოპტიკურ ექსპერიმენტებში კოჰერენტულობის დროზე გაცილებით მეტია (Δt >> τ), სრული გასაშუალოება ხდება. მარეგისტრურებელი მოწყობილობა (თვალი, ფოტოფირფიტა, ფოტოელემენტი ან ნებისმიერი სხვა მიმღები) დაკვირვების მომენტში დააფიქსირებს ინტენსივობის გასაშუალებულ მნიშვნელობას, რომელიც ორივე რხევის ინტენსივობების ჯამის I1 + I2 ტოლია. ამ შემთხვევაში სრულდება ინტენსივობების შეკრების კანონი.
ამგვარად, ინტერფერენცია მხოლოს კოჰერენტილი რხევების შეკრებისას შეიძლება წარმოიქნმას. დაკვირვების წერტილში კოჰერენტული რხევებით მიღებულ ტალღებსაც კოჰერენტულს უწოდებენ. ორი დამოუკიდებელი წყაროს ტალღები არაკოჰერენტულია და ინტერცერენციას ვერ შექმნიან. იუგმა ინტუიციურად მიაგნო, რომ სინათლის ინტერფერენციის მისაღებად საჭიროა წყაროდან მომავალი ტალღა ორ კოჰერენტულ ტალღად უნდა გაიყოს და შემდეგ მათი შეკრების დაკვირვება ეკრანზე უნდა მოხდეს. ასე კეთდება ყველა ინტერფერენციულ სქემაში. მაგრამ ამ შემთხვევაშიც კი, ინტერფერენციული სურათი ქრება, თუ სვლათა Δ სხვაობა კოჰერენტულობის სიგრძეს cτ გადააჭარბებს.
{loadnavigation}
პირველი წარმოდგენა სინათლის ბუნების შესახებ ძველ საბერძნეთსა და ეგვიპტეში შეიმნა. ოპტიკური ხელსაწყოების გამოგონებითა და განვითარებით (პარაბოლური სარკე, მიკროსკოპი, ტელესკოპი) ეს წარმოდგენა ვითარდებოდა და იცვლებოდა. XVII საუკუნის ბოლოს წარმოიშვა ორი თეორია: კორპუსკულული (ი.ნიუტონი) და ტალღური (რ.ჰუკი და ქ.ჰიუგენსი).
კორპუსკულური თეორიის თანახმად, სინათლე წარმოადგენს ნაწილაკების (კორპუსკულების) ნაკადს, რომლებიც მნათი სხეულებიდან გამოდიან. ნიუტონი თვალიდა, რომ სინათლის კორპუსკულების მოძრაობა მექანიკის კანონებს ემორჩილებოდნენ. ამის მიხედვით, სინათლის არეკვლა დრეკადი ბურთულას არეკვლის ანალოგიურია, სინათლის გარდატეხა იხსნებიდა კორპუსკულების სიჩქარის ცვლილებით ერთი გარემოდენ მეორეში გადასვლისას. სინათლის ვაკუუმსა და გარემოს შორის გარდატეხის შემთხვევისთვის კორპუსკულური თეორია გარდატეხის კანონის შემდეგ სახეს იძლეოდა:

სადაც c – ვაკუუმში სინათლე სიჩქარეა, υ – სინათლის გარემოში გავრცელების სიჩქარე. რადგან n > 1, კორპოსკულური თეორიიდად გამოდიოდა რომ სინათლის სიჩქარე გარემოში მეტი უნდა იყოს ვიდრე ვაკუუმში. ნიუტონი ასევე ცდილობდა ინტერფერენციული ზოლების წარმოქმნა სინათლის პროცესებში გარკვეული პერიოდულობის შემოტანის საშუალებით. ამგვარად, ნიუტონის კორპუსკულური თეორია გარკვეულ ტალღურ წარმოდგენებს შეიცავდა.
ტალღური თეორია, კორპოსკულურისგან განსხვავებით, სინათლეს განიხილავს, როგორც მექანიკური ტალღების მსგავს ტალღურ პროცესს. ტალღური თეორიას საფუძვლად დაედო ჰიუგენსის პრინციპი, რომლის მიხედვითაც ყოველი წერტილი რომლამდეც ტალღა აღწევს, მეორადი ტალღის ცენტრი ხდება, ხოლო ამ ტალღების შემომწერი (A1A2 სიბრტყე ნახ. 1-ზე) იძლევა დროის შემდეგ მომენტში ტალღის ფრონტის მდებარეობას. ტალღის ფრონტში გეი-ლუსაკი გულისხმობდა იმ წერტილების გეომეტრულ ადგილს, რომლებამდეც ტალღური შეშფოთება ერთდროულად აღწევს. ამ პრინციპის საშუალებით იქნა ახსნილი არეკვლისა და გარდატეხის კანონები. ნახ. 1-ზe წარმოდგენილია ჰიუგენსის აგებები ორი გამჭვირვალე გარემოს გამყოფ ზედაპირზე გარდატეხილი ტალღის გარკვეული მიმართულებით გავრცელებისთვის.

ნახ. 1.
ჰიუგენსის აგება გარდატეხილი ტალღის გარკვეული მიმართულებისთვის.
სინათლის ვაკუუმსა და გარემოს შორის გარდატეხის შემთხვევისთვის ტალღური თეორია შემდეგ დასკვნამდე მიდის:

ტალღური თეორიიდან მიღებული გარდატეხის კანონი ნიუტონის ფორმულას ეწინააღმდეგება. ტალღურ თეორიას მივყავართ დასკვნამდე: υ < c, მაშინ როცა, კორპუსკულური თეორიის თანახმად υ > c.
ამგვარად. XVIII საუკუნის დასაწისში არსებობდა სინათლის ბუნების ორი ურთიერთსაწინააღმდეგი მიდგომა: ნიოტონის კორპუსკულური თეორია და ჰიუგენსის ტალღური თეორია. ორივე ხსნიდა სინათლის წრფივ გავრცელებას, არეკვლისა და გარდატეხის კანონებს. მთელი XVIII საუკუნე ამ ორი თეორიის ბრძოლის საუკუნედ იქცა. მაგრამ XIX საუკუნის დასაწყისში სიტუაცია მთლიანად შეიცვალა. კორპუსკულური თეორია უარყვეს და ტალღურმა თეორიამ იზეიმა. ამაში დიდ წვლილი ინგლისელ ფიზიკოსს თ.იუნგს და ფრაგ ფიზიკოს ო.ფრენელს მიუძღვით მათ ინტერფერენციის და დიფრაქციის მოვლენები შეისწავლეს. ამ მოვლენების ამომწურავი ახსნა მხოლოს ტალღურ თეორიას შეეძლო. ტალღური თეორიის სამართლიანობის მნიშვნელოვანი ექსპერიმენტული დასაბუთება იყო 1851 წელს ჟ.ფუკოს (და მისგად დამოუკიდებლად ა.ფიზოს) მიერ წყალში სინათლის გავრცელების სიჩქარის გაზომა და მან მიიღო υ < c მნიშვნელოვა.
მიუხედავადიმისა, რომ XIX საუკუნის შუა წლებში ტალღური თეორია საყოველთაოდ მიღებული იყო, საკითხი სინათლის ბუნების შესახებ მაინც ღია რჩებოდა.
XIX საუკუნის 60-იან წლებში მაქსველმა დაადგინა ელექტრომაგნიტური ტალღების საერთო კანონი, საიდანაც მან დაასკვნა, რომ სინათლე ელექტრომაგნიტური ტალღაა. ასეთი თვალსაზრისის მნიშვნელოვანი დასაბუთება სინათლის ვაკუუმში გავრცელების სიჩქარისა და ელექტრომაგნიტურ მუდმივასთან 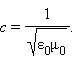 დამთხვევა შეიქმნა. სინათლის ელექტრომაგნიტურმა ბუნებამ ჰერცის ელექტომაგნიტური ტალღების კვლევისთვის ჩატარებული ცდების შემდეგ საყოველთაო აღიარება მოიპოვა (1887-1888).
დამთხვევა შეიქმნა. სინათლის ელექტრომაგნიტურმა ბუნებამ ჰერცის ელექტომაგნიტური ტალღების კვლევისთვის ჩატარებული ცდების შემდეგ საყოველთაო აღიარება მოიპოვა (1887-1888).
სინათლის ბუნების გარკვევაში მნიშვნელოვანი როლი შეასრულა მისი სიჩქარის ცდისეულმა გაზომვებმა. XVII საუკუნის ბოლოდან მოყოლებული სინათლის სიჩქარის სახვადასხვა მეთოდით გაზომვის არაერთი ცდა იქნა ჩატარებული (ა.ფიზოს ასტრონომიული მეთოდი, მაიკელსონის მეთოდი). თანამედროვე ლაზერული ტექნიკა სინათლის სიჩქარის ძალიან დიდი სიზუსტით გაზომვის საშუალებას იძლევა, ტალრის λ სიგრძისა სინათლის ν სიხშირის დამოუკიდებელი გაზომვების ხარჯზე (c = λ · ν). ამგვარი გზით იქნა ნაპოვლი მნიშვნელობა
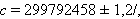
რომელიც სიზუსტით ყველა ადრე მიღებულ მნიშვნელობას ორი რიგით მაინც ჯობნის.
სინათლე ჩვენს ცხოვრებაში განუზომელად დიდ როლს ასრულებს. გარემომცველი გარემოს შესახებ ინფორმაციის ყველაზე მეტ ნაწილს ადამიანი სინათლის საშუალებით იღებს. მაგრამ, ფიზიკის ნაწილში, რომელსაც ოპტიკას ვუწოდებთ, სინათლეში არა მხოლოს ხილული სინათლე იგულისხმება, არამედ მისი მიმდებარე ელექტრომაგნიტური გამოსხივების სპექტრის ფართო დიაპაზონიც - ინფრაწიტელიდან ულტრაიისფერამდე. თვისებების მიხედვით სინათლე პრინციპულად არ განირჩევა ელექტრომაგნიტური გამოსხივების სხვა დიაპაზონებისაგან. სპექტრის სხვადასხვა უბნები ერთმანეთისაგან მხილოდ ტალღის სიგრძითა λ და სიხშირით ν განსხვავდებიან. ნახ. 2-ზე ელექტრომაგნიტური ტალღების შკალაა მოცემული.

ნახ. 2.
ელექტრომაგნიტური ტალღების შკალა. სხვდასხვა დიაპაზონებს შორის საზღვრები პირობითია
ოპტიკურ დიაპაზომში ტალღის სიგრძის გასაზომად გამოიყენება სიგრძის ერთეულები ნანომერტი (ნმ) და მიკრომეტრი (მკმ):
1 ნმ = 10–9 მ = 10–7 სმ = 10–3 მკმ.
ხილული სინათლე დაახლოებით 400-780 ნმ ან 0,40-0,78მკმ დიაპაზონს იკავებს.
სინათლის ელექტრიმაგნიტურმა თეორიამ მრავალი ოპტიკური მოვლენა ახსნა, როგორიცაა ინტერფერენცია, დიფრაქცია, პოლარიზაცია და ა.შ. მაგრამ ამ თეორიამ ვერ შეძლო სინათლის ბუნების ბოლომდე შეცნობა. უკვე XX საუკუნის დასაწყისში გაირკვა, რომ ეს თეორია საკმარისი არ არის ატომის მასშტაბის იმ მოვლენების ასახსნელად, რომლებსაც სინათლის ნივთიერებასთან ურთიერთქმედებისას აქვთ ადგილი. ისეთი მოვლენების შესწავლისთვის, როგორიცაა შავი სხეულის გამოსხივება, ფოტოეფექტი, კომპრონის ეფექტი და სხვა აუცილებელი გახდა ქვანტური წარმოდგენების შემოტანა. მეცნიერება ისევ დაიბრუნდა იდეას კორპუსკულების - სინათლის ქვანტების შესახებ. ის ფაქტი, რომ სინათლე ზოგ ცდაში ტალღურ ბუნებას ავლენს, ხოლო ზოგში კი კორპუსკულურს, ნიშნავს, რომ მას რთული ორმაგი გუნება აქვს, რომელსაც ახასიათებენ ტერმინით კორპუსკულურ-ტალღური დუალიზმი.
