{loadnavigation}
იმისათვის, რომ ატომის ბირთვი მდგრადი იყოს, პროტონები და ნეიტრონები ბირთვში უნდა იყვნენ დაკავშირებული ერთმანეთთან უზარმაზარი ძალებით, ღომლებიც მრავალჯერ აღემატება პროტონების ურთიერთგანზიდვის ძალებს. ბირთვში ნუკლონების შემაკავებელ ძალებს ატომურს უწოდებენ. ისინი წარმოადგენენ ფიზიკაში ცნობილ ურთიერთქმედებათა შორის ყველაზე ინტენსიურს, ე.წ ძლიერ ურთიერთქმედებას. ატომური ძალები დაახლოებით 100-ჯერ აღემატება ელექტრულ ძალებს და ათეული რიგით აღემატება ნუკლონების გრავიტაციულ ურთიერთქმედებას. ატომური ძალების მნიშვნელოვან თავისებურებას წარმოადგენს მათი ახლომოქმედების ხასიათი. ატომური ძალები შესამჩნევად იჩენს თავს, როგორც რეზერფორდის α-ნაწილაკების გაბნევის ცდები უჩვენებენ, მხოლოდ ბირთვის ზომების რიგის (10–12–10–13 სმ) მანძილებზე. დიდ მანძილებზე თავს იჩენს შედარებად ნელად კლებადი კულონის ძალები.
ექსპერიმენტულ ფაქტებზე დაყრდნობით შეიძლება დავასკვნათ, რომ ბირთვში პროტონები და ნეიტრონები ძლიერი ურთიერთქმედების მიმართ ერთნაირად იქცევიან, ე.ი. ატომური ძალები არ არის დამოკიდებული ნაწილაკის მატარებელია თუ არა.
ატომურ ფიზიკაში უმნიშვნელოვანეს როლს ბირთვის ბმის ენერგიის ცნება ასრულებს.
ბირთვის ბმის ენერგია იმ მინიმალური ენერგიის ტოლია, რომელიც საჭიროა ატომის ცალკეულ ნაწილაკებად სრული დაშლისათვის. ენერგიის შენახვის კანონის მიხედვით, ბმის ენერგია ტოლია იმ ენერგიისა, რომელიც გამოიყოფა ცალკეული მაწილაკებისაგან ბირთვის შექმნის შემთხვევაში.
ნებისმიერი ბირთვის ბმის ენერგია მისი მასის ზუსტი გაზომვით შეიძლება განისაზღვროს. დღეისთვის ფიზიკოსებს შეუძლიათ გაზომონ მაწილაკების, ელექტრონის, პროტონის, ნეიტრონის, ბირთვის და ა.შ. მასები, ძალიან დიდი სიზუსტით. ეს გაზომვები უჩვენებენ, რომ ნებისმიერი ბირთვის Mბ მასა ყოველთვის ნაკლებია მასში შემავალი პროტონეისა და ნეიტრონების მასათა ჯამზე:
Mя < Zmp + Nmn.
მასათა სხვაობას
ΔM = Zmp + Nmn – Mя.
მასის დეფექტს უწოდებენ.
მასის დეფექტის მიხედვით ეინშტეინის ფორმულის E = mc2 საშუალებით შეიძლება განისაზღვროს ენეგია, რომელიც მოცემული ბირთვის წარმოქმნისას გამოიყოფა, ე.ი. ბირთვის ბმის Eბმ ენერგია:
Eсв = ΔMc2 = (Zmp + Nmn – Mя)c2.
ბირთვის წარმოქმნისას ეს ენერგია γ-ქვანტების სახით გამოსხივდება.
მაგალითისათვის გამოვთვალოთ ბმის ენერგია ჰელიუმის 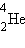 ბირთვისათბვის, რომლის შემადგენლობაშიც შედის ორი პროტონი და ორი ნეიტრონი. ჰელიუმის ბირთვის მასა Mя = 4,00260 მ.ა.ე.-ა. ორი პროტონის და ორი ნეიტრონის მასა შეადგენს 2mp + 2mn = 4, 03298 მ.ა.ე-ს. აქედან გამომდინარე, ჰელიუმის ბირთვის მასის დეფექტი ტოლია ΔM = 0,03038 მ.ა.ე-სი. Eсв = ΔMc2 ფორმულით გათვლას მივყავართ
ბირთვისათბვის, რომლის შემადგენლობაშიც შედის ორი პროტონი და ორი ნეიტრონი. ჰელიუმის ბირთვის მასა Mя = 4,00260 მ.ა.ე.-ა. ორი პროტონის და ორი ნეიტრონის მასა შეადგენს 2mp + 2mn = 4, 03298 მ.ა.ე-ს. აქედან გამომდინარე, ჰელიუმის ბირთვის მასის დეფექტი ტოლია ΔM = 0,03038 მ.ა.ე-სი. Eсв = ΔMc2 ფორმულით გათვლას მივყავართ 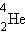 ჰელიუმის ბირთვის ბმის ენერგიის შემდეგ მნიშვნელობამდე: Eсв = 28,3 მევ. ეს უზარმაზარი ენერგიაა. მხოლოდ 1 გ ჰელიუმის წარმოქმნას თან ახლავს 1012 ჯ-ს რიგის ენერგიის გამონთავისუფლება. დაახლოებით იმდენივე ენერგია გამოიყოფა თითქმის მთელი ვაგონი ქვანახშირის დაწვის შედეგად. ატომის ბირთვის ბმის ენერგია მრავალი რიგით აჭარბებს ელექტრონის ატომთან ბმის ებერგიას. მაგალითად, წყალბადის
ჰელიუმის ბირთვის ბმის ენერგიის შემდეგ მნიშვნელობამდე: Eсв = 28,3 მევ. ეს უზარმაზარი ენერგიაა. მხოლოდ 1 გ ჰელიუმის წარმოქმნას თან ახლავს 1012 ჯ-ს რიგის ენერგიის გამონთავისუფლება. დაახლოებით იმდენივე ენერგია გამოიყოფა თითქმის მთელი ვაგონი ქვანახშირის დაწვის შედეგად. ატომის ბირთვის ბმის ენერგია მრავალი რიგით აჭარბებს ელექტრონის ატომთან ბმის ებერგიას. მაგალითად, წყალბადის  ატომისათვის იონიზაციის ენერგია 12,6 ებ-ს ტოლია.
ატომისათვის იონიზაციის ენერგია 12,6 ებ-ს ტოლია.
ცხრილებში მოიცემა ბმის კუთრი ენერგია, ე.ი. ბმის ენერგია ერთი ნუკლონისათვის. ჰელიუმის ბირთვისთვის ბმის კუთრი ენერგია დაახლოებით ტოლია 7,1 მევ/ნუკლონი. ნახ. 1-ზე მბის კუთრი ენერგიის A მასურ რიცხვზე დამოკიდებულების გრაფიკია მოცემული. როგორც გრაფიკიდან ჩანს, ნუკლონების ბმის კუთრი ენერგია სხვადსხვა ატომის ბირთვისთვის ერთნაირი არაა. მსუბუქი ბირთვებისთვის ბმის კუთრი ენერგია თავიდან მკვეთრად იზრდება 1,1 მევ/ნუკლონიდან 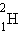 დეიტერიუმისათვის, 7,1 მევ/ნუკლონამდე
დეიტერიუმისათვის, 7,1 მევ/ნუკლონამდე  ჰელიუმისათვის. შემდეგ, რიგი ნახტომების გავლით, ბმის კუთრი ენერგია იზრდება მაქსიმალურ 8,7 მევ/ნუკლონ მნიშვნელობამდე A = 50–60 მასური რიცხვის მქონე ელემენტებისათვის, შემდეგ მძიმე ელემენტებისათვის შედარებით ნელა კლებულობს. მაგალითად,
ჰელიუმისათვის. შემდეგ, რიგი ნახტომების გავლით, ბმის კუთრი ენერგია იზრდება მაქსიმალურ 8,7 მევ/ნუკლონ მნიშვნელობამდე A = 50–60 მასური რიცხვის მქონე ელემენტებისათვის, შემდეგ მძიმე ელემენტებისათვის შედარებით ნელა კლებულობს. მაგალითად, 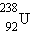 ურანისათვის ის 7,6 მევ/ნუკლონს აღწევს.
ურანისათვის ის 7,6 მევ/ნუკლონს აღწევს.
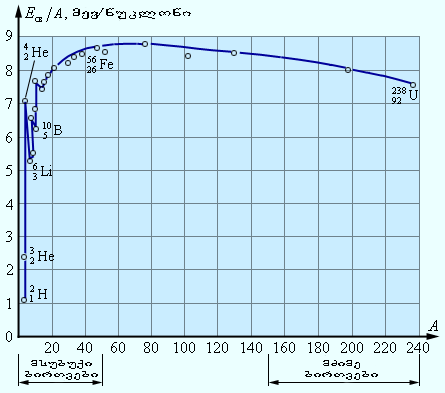
ნახ.1.
ბირთვების ბმის კუთრი ენერგია
მძიმე ელემენტებზე გადასვლისას ბირთვების ბმის კუთრი ენერგიის შემცირება პროტონების კულონური განზიდვის ენერგიის გაზრდით აიხსნება. მძიმე ბირთვებში ნუკლონებს შორის კავშირი სუსტდება, ხოლო თითონ ბირთვები ნაკლებად მდგარადი ხდება.
სტაბულური მსუბუქი ბირთვების შემთხვევაში, სადაც ნუკლონების ურთიერთქმედება დიდი არაა, პროტონების და ნეიტრონების Z და N რიცხვი ერთნაირია ( ,
, 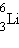 ,
, 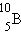 ). ატომური ძალების მოქმედებით იქმნება პროტონ-ნეიტრონული წყვილები. მაგრამ მძიმე ელემენტების ბირთვებს, რომლებშიც პროტონების დიდი რიცხვია, კულონური განზიდვის ენერგიის ზრდის გამო მდგრადობის გაზრდისთვის დამატებითი ნეიტრონები ესაჭიროებათ. ნახ. 2-ზე მოყვანილია დიაგრამა, რომელიც პროტონისა და ნეიტრონების რიცხვს უჩვენებს სტაბილურ ბირთვებში. ბირთვებისთვის, რომლებიც ბისმუტს (Z > 83) მოჰყვებიან, პროტონების დიდი რიცხვის გამო სრული სტაბილურობა შეუძლებელი ხდება.
). ატომური ძალების მოქმედებით იქმნება პროტონ-ნეიტრონული წყვილები. მაგრამ მძიმე ელემენტების ბირთვებს, რომლებშიც პროტონების დიდი რიცხვია, კულონური განზიდვის ენერგიის ზრდის გამო მდგრადობის გაზრდისთვის დამატებითი ნეიტრონები ესაჭიროებათ. ნახ. 2-ზე მოყვანილია დიაგრამა, რომელიც პროტონისა და ნეიტრონების რიცხვს უჩვენებს სტაბილურ ბირთვებში. ბირთვებისთვის, რომლებიც ბისმუტს (Z > 83) მოჰყვებიან, პროტონების დიდი რიცხვის გამო სრული სტაბილურობა შეუძლებელი ხდება.
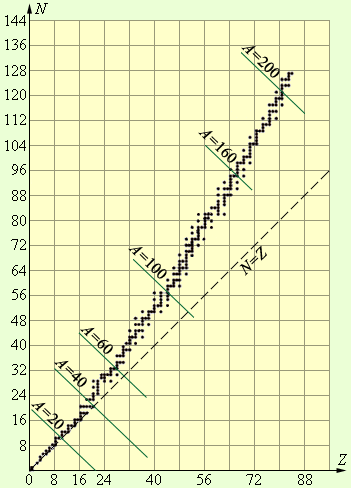
ნახ. 2.
პროტონებისა და ნეიტრონების რიცხვი სტაბილურ ბირთვებში
ნახ.1-დან ჩანს, რომ ენერგეტიკული თვალსაზრისით ყველაზე სტაბილურს წარმოადგენენ მენდელეევის სისტემის შუა ნაწილის ელემენტების ბირთვები. ეს ნიშნავს, რომ ბირთვული გარდაქმნებისას არსებობს დადებითი ენერგიის გამომუშავების ორი შეასაძლებლობა:
1. მძიმე ბირთვების დაყოფა უფრო მსუბუქ ბირთვებად;
2. მსუბუქი ბირთვების შერწმით უფრო მძიმე ბირთვის წარმოქმნა.
ორივე პროცესში ენერგიის უზარმაზარი რაოდენობა გამოიყოფა. დღეისათვის ორივე პროცესი პრაქტიკულადაა განხორციელებული: დაშლის რეაქცია და თერმობირთვული რეაქცია.
შევასრულოთ გარკვეული შეფასება. ვთქვათ, მაგალითად, ურანის 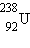 ბირთვი იყოფა ორ ერთნაირ ბირთვად მასური რიცხვით 119. ამ ბირთვების, როგორც ჩანს ნახ.1-დან, ბმის კუთრი ენერგია 8,5 მევ/ნუკლონზე რიგისაა. ურანის ბირთვის ბმის კუთრი ენერგია 7,6 მევ/ნუკლონზეა. აქედან გამომდინარე, ურანის ბირთვის გაყოფისას გამოყოფილი ენერგია ტოლია 0,9 მევ/ნუკლონზეა ან 200 მევ ურანის ერთ ატომზე.
ბირთვი იყოფა ორ ერთნაირ ბირთვად მასური რიცხვით 119. ამ ბირთვების, როგორც ჩანს ნახ.1-დან, ბმის კუთრი ენერგია 8,5 მევ/ნუკლონზე რიგისაა. ურანის ბირთვის ბმის კუთრი ენერგია 7,6 მევ/ნუკლონზეა. აქედან გამომდინარე, ურანის ბირთვის გაყოფისას გამოყოფილი ენერგია ტოლია 0,9 მევ/ნუკლონზეა ან 200 მევ ურანის ერთ ატომზე.
ახლა მეორე პროცესი განვიხილოთ. ვთქვათ გარკვეულ პირობებში დეიტერიუმ 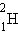 ორი ბირთვის შერწყმით
ორი ბირთვის შერწყმით  ჰელიუმის ერთი ბირთი წარმოიქმნა. დეიტერიუმის ბირთვების ბმის კუთრი ენერგია ტოლია 1,1 მევ/ნუკლონზე, ხოლო ჰელიუმის ბირთვების ბმის კუთრი ენერგია 7,1 მევ/ნუკლონზე. აქედან გამომდინარე, დეიტერიუმის ორი ბირთვისაგან ჰელიუმის ერთი ბირთვის სინთეზისას გამოყოფილი ენერგია ტოლია 6 მევ/ნუკლონზე ან 24 მევ ჰელიუმის ერთ ატომზე.
ჰელიუმის ერთი ბირთი წარმოიქმნა. დეიტერიუმის ბირთვების ბმის კუთრი ენერგია ტოლია 1,1 მევ/ნუკლონზე, ხოლო ჰელიუმის ბირთვების ბმის კუთრი ენერგია 7,1 მევ/ნუკლონზე. აქედან გამომდინარე, დეიტერიუმის ორი ბირთვისაგან ჰელიუმის ერთი ბირთვის სინთეზისას გამოყოფილი ენერგია ტოლია 6 მევ/ნუკლონზე ან 24 მევ ჰელიუმის ერთ ატომზე.
ყურადღება უნდა მიექცეს იმას, რომ მსუბუქი ბირთვების სინთეზისას მძიმე ბირთვების გაყოფასთან შედარებით 6-ჯერ უფრო დიდი ენერგია გამოიყოფა ყოველ ერთ ნუკლონზე.
{loadnavigation}
XX საუკუნის 20-იან წლებისთვის ეჭვი უკვე არავის ეპარებოდა, რომ ატომის ბირთვი, რომელიც რეზერფორდმა 1911 წელს აღმოაჩინა, ისევე როგორც ატომი, რთული სტრუტურის იყო. ამაზე ამ დროისთვის დაგროვილი მრავალრიცხოვანი ექსპერიმენტული ფაქტები მიუთითებდნენ: რადიოაქტივობის აღმოჩენა, ატომის ბირთვული მოდელის ექსპერიმენტული დასაბუთება, e / m ფარდობის განსაზღვრა ელექტრონისთვის, ატომის ბირთვის α -ნაწილაკებისა და ე.წ. H -ნაწილაკებისათვის, ხელოვნური რადიაქტივობისა და ბირთვული რეაქციის აღმოჩენა, ატომური ბირთვის მუხტის გაზომვები და ა.შ.
დღეისთვის მკაცრადაა დადგენილი, რომ სხვადასხვა ელემენტების ატომის ბირთვები ორი სახის ნაწილაკებისგან - პროტონებისა და ნეიტრონებისაგან შედგებიან.
ამ ნაწილაკებიდან პირველი ელექტრონ მოცილებულ წყალბადის ატომს წარმოადგენს. ეს ნაწილაკი 1907 წლიდან დაიკვირვება ტომსონის ცდებში, რომელმაც მისი e / m ფარდობის გაზომვა მოახერხა. 1919 წელს რეზერფორდმა წყალბადის ატომის ბირთვი მრავალი ელემენტის ბირთვის გახლეჩის პროდუქტებს შორის აღმოაჩინა. ამ ნაწილაკს რეზერფორდმა პროტონი უწოდა. მან გამოთქვა მოსაზრება, რომ პროტონი ყველა ატომის ბირთვის შემადგენლობაში შედის. რეზერფორდის ცდების სქემა ნახ. 1-ზეა მოცემული.

ნახ. 1.
ატომის გახლეჩვის პროდუქტებს შორის პროტონის აღმოჩენის რეზერფოდისეული ცდის სქემა. α-ნაწილაკების რადიოაქტიური წყაროთი, Ф – მეტალის თხელი ფირფიტა, Э – თუთიის სულფიდით დაფარული ეკრანი, М – მიკროსკოპი
რეზერფორდის ხელსაწყო შედგება ვაკუუმური კამერისგან, რომელშიც α-ნაწილაკების რადიოაქტიური წყაროს შემცველი К ტყვიის კონტეინერია მოთავსებული. კამერის სარკმელი დაფარული იყო Ф მეტალის თხელი ფირფიტით, რომლის სისქეც ისე იყო შერჩეული, რომ α-ნაწილაკებს შიგ ვერ გაევლოთ. სარკმლის უკან მოთავსებულია თუთიის სულფიდით დაფარული Э ეკრანი. М მიკრისკოპის საშუალებით შესაძლებელი იყო ეკრანზე მძიმე დამუხტულის ნაწილაკების დაჯახების წერტილებში სცინტილაციის (ე.წ. მცირე ნათებების) დაკვირვება. კამერის დაბალი წნევით აზოტით ავსებისას ეკრანზე ნათებები გამოჩნდება, რაც რაღაც ნაწილაკების ნაკადის გამოჩენაზე მიუთითებს, რომლებსაც შეუძლიათ იმ Ф ფირფიტაში გასვლა, რომელიც თითქმის სრულად აკავებს α-ნაწილაკებს. ეკრანის კამერის სარკმლიდან გაწევის საშუალებით რეზერფორდმა გაზომა დაკვირვებული ნაწილაკების თავისუფალი განარბენის საშუალო სიგრძე ჰაერში. ის დაახლოებით 28 სმ აღმოჩნდა, რაც ტომსონის მიერ დაკვირვებული H-ნაწილაკების განარბების შეფასებებს ემთხვევა. აზოტის ატომის ბირთვებიდან ამოყრილ ნაწილაკებზე ელექტრული და მაგნიტური ველების ზემოქმედების შესწავლამ უჩვენა, რომ ეს ნაწილაკები დადებითი მუხტით ხასიათდებიან და მათი მასა წყალბადის ატომის ბირთვის მასის ტოლია. შემდგომში ცდა განმეორდა მთელი რიგი სხვა აირადი ნივთიერებებისთვის. ყველა შემთხვევაში აღმოჩნდა, რომ ამ ნივთიერებების ატომების ბირთვებიდან α-ნაწილაკები H-ნაწილაკებს ანუ პროტონებს ამოყრიან.
თანამედროვე გაზომვების მოხედვით პროტონის დადებითი მუხტი ზუსტად ელემენტარული მუხტის e = 1,60217733·10–19 კ ტოლია. ე.ი. მოდულით ელექტრონის უარყოფითი მუხტის ტოლია. დღეისათვის პროტონისა და ელექტრონის მუხტების ტოლობა შემოწმებულია 10–22 სიზუსტით. ორი ასე განსხვავებული ნაწილაკის მუხტების ასეთი დამთხვევა გაოცებას იწვევს და თანამედროვე ფიზიკის ფუნდამენტურ გამოცანად რჩება.
პროტონის მასა, თანამედროვე გაზომვებით, mp = 1,67262∙10–27კგ-ს ტოლია. ბირთვულ ფიზიკაში ნაწილაკების მასები ხშირად იზომება მასის ატომურ ერთეულებში (მ.ა.ე.), რომელიც ნახშირბადის (მასური რიცხვი 12) ატომის მასის 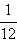 -ია:
-ია:
1 მ.ა.ე. = 1,66057·10–27 კგ.
აქედან გამომდინარე, mp = 1,007276 მ.ა.ე-ა. ბევრ შემთხვევაშინაწილაკების მასები ხელსაყრელია, E = mc2 ფორმულის შესაბამისად, ენერგიის ექვივალენტურ მნიშვნელობებში გამოისახოს. რადგანაც 1 ევ=1,60218·10–19 ჯ-ს. ენერგეტიკულ ერთეულებში პროტონის მასა 938,272331 მევ-ს ტოლია.
ამგვარად, რეზერფორდის ცდებით აღმოჩენილი იქნა აზოტისა და სხვა ელემენტების ატომის ბირთვების გახლეჩვაის მოვლენა წრაფ α-ნაწილაკებთან დაჯახების შედეგად და ნაჩვენები იქნა, რომ პროტონები ატომების ბირთვების შემადგენლობაში შედიან.
პროტონის აღმოჩენის შემდეგ გამოითქვა მოსაზრება, რომ ატომების ბირთვები მხოლოდ პროტონებისგან შედგებოდნენ. მაგრამ ეს ვარაუდი ვერ გამართლდა, რადგან ატომბირთვის მუხტის ფარდობა მის მასასთან არ არის მუდმივი სხვადასხვა ბირთვებისათვის, რასაც იმ შემთხვევაში ექნებოდა ადგილი, ბირთვი მარტო პროტონებისგან რომ შედგებოდეს. უფრო მძიმე ბირთვებისათვის ეს ფარდობა ნაკლები გამოდის, ვიდე მსუბუქებისათვის, ე.ი. მძიმე ბირთვებზე გადასვლისას ბირთვის მასა უფრო სწრაფად იზრდება, ვიდრე მუხტი.
1920 წელს რაზერფორდმა გამოთქვა ჰოპოთეზა ბირთვში ერთმანეთთან მყარად დაკავშირებული პროტონ-ელექტრონის წყვილის არსებობის შესახებ, რომელიც ელექტრულად ნეიტრალურ წარმონაქმნს წარმოადგენს, რომლის მასა დაახლოებით პროტონის მასის ტოლია. მან ამ ჰიპოტეტური ნაწილაკის სახელიც კი მოიფიქრა - ნეიტრონი. ეს ძალიან ლამაზი, მაგრამ, როგორც შემდგომში აღმოჩნდა, მცდარი იდეა იყო. ელექტრონს არ შეუძლია შედიოდეს ბირთვის შმადგენლობაში. განუზღვრელობების თანაფარდობებზე დამყარებული ქვანტურ-მექანიკური გათვლები უჩვენებენ, რომ ბირთვში ლოკალიზებულ ელექტრონს, ე.ი. არეს ზომებით R ≈ 10–13 სმ, უნდა ჰქონდეს კოლოსალური კინეტიკური ენერგია, რომელიც მრავალი რიგით უნდა აღემატებოდეს ერთ ნაწილაკზე გათვლილ ბირთვის ბმის ენერგიას. მაგრამ მძიმე ნეიტრალური ნაწილაკის არსებობა რეზერფორდს იმდენად მიმზიდველად ეჩვენებოდა, რომ მან თავისი მოსწავლეებს ჯგუფს ჯ.ჩედვიკის ხელმძღვანელობით დაუყოვნებლივ შესთავაზა დაეწყო მისი ძებნა. 12 წლის შემდეგ, 1932 წელს, ჩედვიკმა ექსპერიმენტულად გამოიკვლია გამოსხივება, რომელის ბერილიუნის α-ნაწილაკებით დასხივებისას წარმოიქმნება, და აღმოაჩინა, რომ ეს გამოსხივება ნეიტრალური ნაწილაკების ნაკადს წარმოადგენს, რომელთა მასა დაახლოებით პროტონის მასის ტოლია. ასე აღმოჩნდა ნეიტრონი. ნახ 2-ზე ნეიტრონის აღმოჩენის დანადგარის გამარტივებული სქემაა მოცემული.

ნახ. 2.
ნეიტრონის აღმოჩენის დანადგარის სქემაა
ბერილიუმის α-ნაწილაკებით დაბომბვისას რადიაქტიური პოლონიუმის მიერ ამოფრქვეული ნაწილაკებით წარმოიქმნება ძლიერ გამჭოლი ნაკადი, რომელსაც შეუძლია გადალახოს ისეთი წინაღობა, როგორიცაა ტყვიის 10-20 სმ-იანი ფენა. ამ გამოსხივებას, ჩედვიკთან თითქმის ერთდროულად, აკვირდებოდნენ ცოლ-ქმარი ირენ და ფრედერიკ ჟოლიო-კიურები (ირენი მარია და პიერ კიურების ქალიშვოლია), მაგრამ მათ იფიქრეს, რომ დიდი ენერგიის მქონე γ-სხივები იყო. მათ ნახეს, რომ თუ ბერილიუბის გამოსხივების გზაზე პარაფინის ფირფიტას მოვათავსებთ ამ გამოსხივების მაიონიზირებელი თვისება მკვეთრად გაიზრდება. მათ დაამტკიცეს, რომ ბერილიუმის გამოსხივება პარაფინიდან ამოყრის პროტონებს, რომლების მრავლადაა ამ, წყალბადის შემცველ ნივთიერებაში. პროტონების ჰაერში თავიუფალი განარბენის საშუალებით მათ შეაფასეს γ-ქვანტების ენერგია, რომლებსაც დაჯახებისას შეეძლოთ პროტონებისთვის საჭირო სიჩქარის მინიჭება. ის უზარმაზარი აღმოჩნდა - 50 მევ-ს რიგის.
1932 წელს ჩედვიკმა ბერილიუმის α-ნაწილაკებით დაბომბვისას წარმოქმნილი გამოსივების ყოველმხრივი შსწავლისთვის შეასრულა ექსპერიმენტების სერია. თავის ცდებში ის მაიონიზირებელი გამოსხივებების გამოკვლევის სხვადასხვა მეთოდს იყენებდა. ნახ. 2-ზე გეიგერის მთვლელია გამოსახული, რომელიც დამუხტული ნაწილაკების აღმოჩენისთვისაა განკუთვნილი. იგი შედგება მინის მილისაგან, რომელიც შიგნიდან მეტალის ფენითაა დაფარული (კათოდი), მილის ღერძის გასწვრის დამაგრებულია წვრილი ძაფი (ანოდი). მილი დაბალი წნევის ინერტული აირითაა შევსებული (ჩვეულებრივ არგონით). დამოხტული ნაწილაკი, აირში გავლისას, მოლეკულების იონიზაციას იწვევს. იონიზაციის შედეგად გამონთავისუფლებული თავისუფალი ელექტრონები ანოდისა და კათოდის ელექტრულ ველში ჩქარდებიან ენერგიამდე, რომლის შემდეგაც იწყება დარტყმითი იონიზაცია. წარმოიქმნება იონების ზვავი, და მთვლელში გაივლეს იმპულსური დენის მოკლე განმუხტვა. ნაწილაკების შესწავლისთვის მეორე მნიშვნელოვან ხელსაწყოს ვილსონის კამერა წარმოადგენს, რომელშის სწრაფი დამუხტული ნაწილაკი კვალს (ტრეკს) ტოვებს. ნაწილაკის ტრაექტორიაზე დაკვირვება შესაძლებელია პირდაპირ ან მისი ფოტოგრაფირების საშუალებით. ვილსონის კამერის მოქმედება, რომელიც 1912 წელს შეიქმნა, დამყარებულია კამერის მუშა მოცულობაში დამუხტული ნაწილაკის ტრაექტორიის გასწვრის წარმოქმნილი გაჯერებული ორთქლის იონებზე კონდენსაციაზე. ვილსონის კამერის საშუალებით შესაძლებელია ელექტრულ და მაგნიტურ ველში დამუხტული ნაწილაკის ტრაექტორიის გამრუდების დაკვირვება.
ჩედვიკი ვილსონის კამერაში აკვირდებოდა აზოტის ბირთვების ტრეკებს, რომლებიც ბერილიუმის გამოსხივებასთან შეჯახებას განიცდიდა. ამ ცდების საფუძველზე მან შეაფასა γ-კვანტის ენერგიის შეფასება, რომელსაც შეუძლია აზოტის ბირთვებს ექსპერიმენტით დაკვირვებული სიჩქარე მიანიჭოს. ის 100-150 მევ აღმოჩნდა. ასეთი დიდი ენერგია არ შეიძლება ჰქონდეს ბერილიუმიდან ამოფრქვეულ γ-ქვანტს. ამის საფუძველზე ჩედვიკმა დაასკვნა, რომ α-ნაწილაკების ზემოქმედებით ამოიფრქვევა არა უმასო γ-კვანტი, არამედ საკმარისად მძიმე ნაწილაკები. ამ ნაწილაკებს აქვთ დიდი შეღწევის უნარი და პირდაპირ არ მოუხდენიათ აირის იონიზაცია გეიგერის მთვლელში, და აქედან გამომდინარე, ელექტრულად ნეიტრალურია. ასე დამტკიცდა ნეიტრონის არსენობა.
ნეიტრონი ელემენტარული ნაწილაკია. თანამედროვე გაზომვების მიხედვით, ნეიტრონის მასა mn = 1,67493∙10–27 კგ = 1,008665 მ.ა.ე. ენერგეტიკულ ერთეულებში ნეიტრონის მასა 939,56563 მევ-ს ტოლია. ნეიტრონის მასა დაახლოებით ორი ელექტრონის მასით ჭარბობს პროტონის მასას.
ნეიტრონის აღმოჩენისთანავე წამოყენებული იქნა ჰიპოთეზა ატომის ბირთვის პროტონ-ნეიტრონული აგებულების შესახებ, რომელიც შემდგომი გამოკვლევებით მთლიანად დასაბუთდა. პროტონებსა და ნეიტრალურონებს ნუკლონებს უწოდებენ.
ატომის ბირთვის დახასიათებისთვის შემოღებულია რიგი აღნიშვნები. ატომში შემავალი პროტონების რიცხვი აღინიშნება Z-ით და მუხტის რიცხვი ან ატომური ნომერი ეწოდება (ეს მენდელეევის პერიოდულ ცხრილში რიგითი ნომერია). ბირთვის მუხტი ტოლია Ze, სადაც e – ელემენტარული მუხტია. ნეიტრონების რიცხვი აღინიშნება N სიმბოლოთი.
ნუკლონების საერთო რიცხვს (ე.ი. პროტონებისა და ნეიტრონების) A მასურ რიცხვს უწოდებენ:
A = Z + N.
ქიმიური ელემენტის ბირთვს აღნიშნავენ 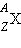 , სადაც X – ქიმიური ელემენტის სიმბოლოა. მაგალითად,
, სადაც X – ქიმიური ელემენტის სიმბოლოა. მაგალითად, 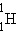 - წყალბადი,
- წყალბადი, 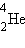 - ჰელიუმი,
- ჰელიუმი, 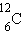 -ნახშირბადი,
-ნახშირბადი, 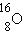 - ჟანგბადი,
- ჟანგბადი, 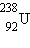 - ურანი.
- ურანი.
ერთიდაიგივე ელემენტის ბირთვები შეიძლება განსხვავდებოდეს ნეიტრონების რიცხვის მიხედვით. ასეთ ბირთვებს იზოტოპები ეწოდებათ.ქიმიური ელემენტების უმრავლესობას რამოდენიმე იზოტოპი აქვს. მაგალითად, წყალბადს სამი იზოტოპი აქვს: 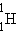 - ჩვეულებრივი წყალბადი,
- ჩვეულებრივი წყალბადი,  - დეიტერიუმი და
- დეიტერიუმი და  - ტრიტიუმი. ნახშირბადს 6 იზოტოპი, ჟანგბადს -3.
- ტრიტიუმი. ნახშირბადს 6 იზოტოპი, ჟანგბადს -3.
ბუნებრივ პირობებში ქიმიური ელემენტები ჩვეულებრივ იზოტოპების ნარევს წარმოადგენენ. იზოტოპების არსებობა განსაზღვრავს ბუნებაში არსებული ელემენტების ატომურ მასას მენდელეევის პერიოდულ სისტემაში. ასე, მაგალითად, ბუნებრივი ნახშირბადის ფარდობითი ატომური რიცხვი 12,011-ის ტოლია.
{loadnavigation}
ლაზერები ან ოპტიკურ ქვანტური გენერატორი კოჰერენტული გამოსხივების თანამედროვე ხელსაწყოა, რომელსაც მთელი რიგი უნიკალური თვისებები აქვს. ლაზერის შექმნა XX საუკუნის მეორე ნახევრის ფიზიკის მიღწევაა, რომელმაც ნეცნიერებისა და ტექნიკის ბევრი დარგი რევოლუციურ ცვლილება გამოიწვია. დღეისთვის შექმნილია ლაზერების დიდი რაოდენობა - აირის, მყარსხეულოვანი, ნახევარგამტარული, რომლებსაც სხვადსხვა მახასიათებლები აქვთ და სხვადასხვა ოპტიკურ დიაპაზონში ასხივებენ. ლაზერებს შეუძლიათ მუშაობა იმპულსურ და უწყვეტ რეჟიმში. ლაზერების გამოსხივების სიმძლავრე შეიძლება იცვლებოდეს მილივატის ნაწილიდან 1012–1013 ვტ-მდე (იმპულსურ რეჟიმში). ლაზერები ფართოდ გამოიყენება სამხედრო ტექნიკაში, მასალების დამუშავების ტექნოლოგიებში, მედიცინაში, ნავიგაციის ოპტიკურ სისტემენში, კავშირგაბმულობასა და ლოკაციაში, პრეციზიულ ინტერფერენციულ ექსპერიმენტებში, ქიმიაში, უბრალოდ ყოფაცხოვრებაში და სხვა. მიუხედავად იმისა, რომ პირველი ოპტიკურ ქვანტური გენერატორი არც ისე დიდი ხნის წინ შიქმნა (1960 წ.), თანამედროვე ცხოვრება ლაზერების გარეშე წარმოუდგენელია.
ლაზერული გამოსხივების ერთ-ერთი უმნიშვნელოვანესი თვისებაა მისი მონოქრომატულობის განსაკუთრებულად დიდი ხარისხი, რომელიც სხვა წყაროების საშუალებით მიუღწეველია. ლაზერული გამოსხივების ეს და სხვა უნიკალური თვისებები იქმნება მუშა ნივთიერების მრავალი ატომის მიერ სინათლის ქვანტების კოოპერატიული ამოფრქვევით.
ლაზერის მუშაობის პრინციპის გასაგებად უფრო ყურადღებით უნდა იქნეს შესწავლილი ატომების მიერ სინათლის ქვანტების შთანთქმისა და გამოსხივების პროცესები. ატომები შეიძლება იმყოფებოდნენ განსხვაბებულ მდგომარეობებში ენერგიებით E1, E2 და ა.ს. ბორის თეორიაში ამ მდგომარეობებს სტაბილურს უწოდებენ. სინამდვილეში სტაბილური მდგომარეობა, რომელშიც ატომი გარე შემაშფოთებლის არ არსებობის შემთხვევაში შეიძლება უსასრულოდ დიდხანს იმყოფებოდეს, მხოლოდ უმცირესი ენერგიის შესაბამისი მდგომარეობაა. ამ მდგომარეობას ძირითადს უწოდებენ. ყველა სხვა მდგომარეობა არასტაბილურია. აღგზნებული ატომი ამ მდგომარეობაში შეიძლება იმყოფებოდეს მხოლოს ძალიან მცირე 10–8 წამის რიგის დროით, ამის შემდეგ ის ქვანტის ამოფრქვევის შედეგად თავისთავად გადადის ერთ-ერთ ქვედა მდგომარეობაში. ამ ქვანტის სიხშირე ბორის მეორე პოსტულატის საშუალებით შეიძლება განისაზღვროს. ატომის ერთი მდგომარეობიდან მეორეში თვითნებული გადასვლისას ამოფრქვეულ გამოსხივებას სპონტანურს უწოდებენ. ზოგიერთ ენერგეტიკულ დონეზე ატომი შეიძლება იმყოფებოდეს 10–3 წამის რიგის დროზე გაცილებით დიდი ხნის განმავლობაში. ასეთ დონეებს მეტასტაბილურს უწოდებენ.
ატომის უფრო მაღალ ენერგეტიკულ დონეზე გადასვლა შეიძლება მოხდეს იმ ფოტონის რეზონანსული შთანთქმისას, რომლის ენერგიაც ატომის საბოლოო და საწყისი მდგომარეობების ენერგიების სხვაობის ტოლია.
ატომის ენერგეტიკულ დონეებს შორის გადასვლა აუცილებლად არაა დაკავშირებული ფოტონების შთანთქმასა და ამოფრვევაზე. ატომს შეუძლია მიიღოს ან გასცეს ენერგიის ნაწილი და გადავიდეს სხვა ქვანტურ მდგომარეობაში სხვა ატომებთან ურთიერთქმედების შედეგად ან ელექტრონებთან შეტაკებისას. ასეთ გადასვლებს გამოსხივების გარეშეს უწოდებენ.
ახლა ყველაზე მთავარი. 1916 წელს აინშტაინმა იწინასწარმეტყველა, რომ ატომში ელექტრონის მაღალი ენერგეტიკული დონიდან დაბალზე გადასვლა შეიძლება ხდებოდეს იმ გარე ელექტრომაგნიტური ველის გავლენით, რომლის სიხშირეც გადასვლის საკუთარი სიხშირის ტოლია. ამ დროს წარმოქმნილ გამოსხივებას იძულებით ან ინდუცირებულს უწოდებენ. იძულიბით გამოსხივებას გასაოცარი თვისება ახასიათებს. ის ძალიან განსხვავდება სპონტანური გამოსხივებისგან. აღგზნებული ატომის ფოტონთან ურთიერთქმედების შედეგად ატომი იგივე სიხშირის კიდევ ერთ ფოტონს ასხივებს, რომელიც იგივე მიმართულებით ვრცელდება. ტალღური თეორიის ენაზე ეს ნიშნავს, რომ ატომი ელექტრომაგნიტურ ტალღას ასხივებს, რომლის სიხშირე, ფაზა, პოლარიზაცია და გავრცელების მიმართულება ხშირად ზუსტად საწყისი ტალღისას ემთხვევა. ფოტონების იძულებითი ამოფრქვევის შედეგად გარემოში გავრცელებული ტალღის ამპლიტუდა იზრდება. ქვანტური თეორიის თვალსაზრისით, აღგზნებული ატომის ისეთ ფოტონთან ურთიერთქმედების შედეგად, რომლის სიხშირე გადასვლის სიხშირის ტოლია, წარმოიქმნება ორი სრულიად ერთნაირი ტყუპი ფოტონი.
სწორედ გამსხივების ინდუცირება წარმოადგენს ლაზერების მუშაობის ფიზიკურ საფუძველს.
ნახ. 1-ზე სქემატურადაა წარმოდგენილი ატომის ორ ენერგეტიკულ დონეს შორის გადასვლის მექანიზმები ან ქვანტის ამოფრქვევა.

ნახ. 1.
პროცესების პირობითი გამოსახულება (a) შთანთქმა, (b) სპონტანური ამოფრქვევა და (c) ქვანთის ინდუცირებული ამოფრქვევა.
განვიხილოთ გამჭვირვალე ნივთიერების ფენა, რომლის ატომებიც შეიძლება იმყოფებოდნენ E1 და E2 > E1 ენერგეტიკულ მდგომარეობებში. ამ ფენებში ვრცელდება გადასვლის რეზონანსული ν = ΔE / h სიხშირის გამოსხივება. ბოლცმანის განაწილების თანხმად, თერმოდინამიკური წონასწორობისას ნივთიერების ატომების დიდი რაოდენობა ქვედა ენერგეტიკულ მდგომარეობაში იმყოფება. ატომენის რაღაც ნაწილი, სხვა ატომებთან შეჯახებებით ღებულობს რა საკმარის ენერგიას, ზედა ენერგეტიკულ მდგომარეობაშიც იმყოფება. ქვედა და ზედა დასახლებები აღვნიშნოთ n1 და n2 < n1 შასბაბისად. ასეთ გარემოში რეზონანსული გავრცელებისას ადგილი ექნება ნახ. 1-ზე გამისახულ სამივე პროცესს. აინშტაინმა უჩვენა, რომ ფოტონის აღუგზნები ატომის მიერ შთანთქმის (a) პროცესს და აგზნებული ატომის მიერ ქვანტის ინდუცირებული ამოფრქვევის (c) პროცესს ერთნაირი ალბათობა აქვს. რადგან n2 < n1 ფოტონის შთანთქმა მოხდება უფრო ხშირად, ვიდრე ამოფრქვევის ინდუცირება. ამის შედეგად ნივთიერების ფენაში გავლის შემდეგ გამოსხივება თანდათან შესუსტდება. ეს მზის გამოსხივების სპექტრში ფრაუნგოფერის ბნელი ხაზების წარმოქნმას მოგვაგონებს. სპონტანური გადასვლების შედეგად წარმოქმნილი გამოსხივება კოჰერენტული არ არის, ნებისმიერი მიმართულებით ვრცელდება და ფენაში გავლილ ტალღაში წვლილი არ შეაქვს.
ნივთირერების ფენაში გავლილი ტალღა რომ გაძლიერდეს, ხელოვნურად უნდა შეიქმნას პირობა, რომლის დროსაც n2 > n1, ე.ი. შეიქმნას დონის ინვერსიული დასახლება. ასეთი გარემო თერმოდინამიკურად გაუწონასწორებელია.
გარემოს, რომელშიც დონეების ინვერსიული დასახლება იქმნება, აქტიურს უწოდებენ. იგი შეიძლება გამოყენებულ იქნეს სინათლის სიგნალის გამაძლიერებლად. იმისათვის რომ შეიქმნას სინათლის გენერაცია უკუკავშირის გამოყენებაა აუცილებელი. ამისათვის აქტიური გარემო ორ მაღალხარისხოვან სარკეს შორის უნდა მოთავსდეს, რომლების სინათლეს მკაცრად უკან არეკლავს ისე, რომ მან მარავალჯერადად გაიაროს აქტიურ გარემოში, რაც გამოიწვევს კოჰერენტული ფოტონების ინდუცირებული ემისიის ზვავისებურ პროცესს. ამ დროს გარემოში უნდა ხდებოდეს დონენების ინვერსიული დასახლების უზრუნველყოფა. ამ პროცესს ლაზერულ ფიზიკაში (დატუმბვას) უწოდებენ.
ასეთ სისტემაში ზვავისებური პროცესის დაწყებას გარკვეულ პირობებში შეიძლება ისეთმა შემთხვევითმა სპონტანურმა აქტმა მისცეს ბიძგი, რომლის დროსაც წარმოიქმნება სისტემის ღერძის გასწვრივ მიმართული გამოსხივება. გარკვეული დროის შემდეგ ასეთ სისტემაში გენარეციის სტაციონალური რეჟიმი მყარდება cialis over the counter. სწორედ ესაა ლაზერი. ლაზერის გამოსხივების გარეთ გამოყვანა ერთი ან ორივე სარკიდან ხდება, რომლებსაც ნაწილობრივი გამჭვირვალობა აქვთ. ნახ. 2-ზე სქემატურადაა წარმოდგენილი ლაზერში ზვავური პროცესის განვითარების პროცესი.

ნახ. 2.
ლაზერში გენარაციის ზვავისებური პროცესის განვითარება
დონეენის ინვერსიული დასახლების მქონე გარემოს შექმნის სხვადასხვა ხერხები არსებობს. ლალის ლაზერში ოპტიკურ დატუმბვას იყენებენ, ატომების სინათლის შთანთქმის ხარჯზე აღიგზნება. მაგრამ ამისათვის მხილოდ ორი დონე საკმარისი არაა. დატუმბვის ნათურის სინათლე როგორი ძლიერიც არ უნდა იყოს, აღგზნებული ატომების რიცხვი აღუგზნებად ატომებზე მეტი არ იქნება. ლალის ლაზერში დატუმბვა ხდრბა ზევით მდებარე მესამე დონიდან (ნახ. 3).
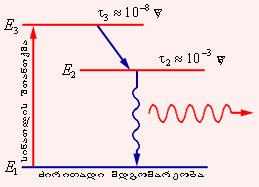
ნახ. 3.
ოპტიკური დატუმბვის სამდონიანი სქემა. მითითებულია E2 და E3 დონეების „სიცოცხლის ხანგრძლივობა“ . E2 დონე მეტასტაბულურია. E3 და E2 დონეებს შორის გადასვლისას გამოსხივება არ ახლავს. ლაზერული გადასვლა E2 და E1 დონეებს შორის ხდება. ლალის კრისტალში E1, E2 და E3 დონეები ქრომის მინარევს ეკუთვნის
ლალის ღეროს მძლავრი ნათურით დანათების შემდეგ ლალის კრისტალში მინარევის სახით შემავალი ქრომის მრავალი ატომი E3 ენერგიის მდგომარეობაში გადადის, ხოლო τ ≈ 10–8 წმ შუალედის შემდეგ E2 ენერგიის შესაბამის მდგომარეობაში. აღგნებულის E2 დონის დასახლების სიჭარბე აღუგზნებელი E1 დონესთან შედარებით E2 დონის შედარებით უფრო დიდი სიცოცხლის ხანგრძლივობის გამო წარმოიქმნება.
ლალიანი ლაზერები იმპულსურ რეჟიმში მუშაობენ 694 მმ ტალღის სიგრძეზე (მუქი ალუბლუსფერი სინათლე), იმპულსში გამოსხივების სიმძლავრე შეიძლება აღწევდეს 106–109 ვტ-ს. ისტორიულად ეს იყო პირველი მომქმედი ლაზერი, რომერლიც ამერიკელბა ფიზიკოსმა მაიმანმა ააგო 1960 წელს.
დღეისათვის ყველაზე გავრცელებულია აირის ლაზერია, რომელიც ჰელიუმისა და ნეონის ნარევზე მუშაობს. He-სა და Ne-ს ნარევის 10 : 1თანაფარდობის პირობებში ნარევის საერთო წნევა 102 პა-ს რიგისაა. აქტიურ აირს, რომელშიც 632,8ნმ ტალღის სიგრძეზე უწყვეტ რეჟიმში აღიძვრება გენერაცია (ღია-წითელი სინათლე), ნეონი წარმოადგენს. ჰელიუმი ბუფერული აირია, იგი მონაწილეობს ნეონის ერთ-ერთი ზედა დონის ინვერსიულ დასახლების პროცესში. He–Ne ლაზერის გამოსხივება ხასიათდება საუცხოო, განუმეორებელი მონოქრომატულობით. გამოთვლები უჩვენებენ, რომ He–Ne ლაზერის სპექტრული ხაზის სიგანე დაახლოებით Δν ≈ 5·10–4 ჰც-ს შეადგენს. ეს ფანტასტიურას მცირე სიგანეა. ასეთი გამოსხივების კოჰერენტულობის დრო τ ≈ 1 / Δν ≈ 2·103 წმ-ს რიგისაა, ხოლო კოჰერენტულობის სიგრძე cτ ≈ 6·1011 მ, ე.ი. დედამიწის ორბიტის დიამეტრზე მეტი!
პრაქტიკაში მრავალი ტექნიკური მიზეზი ხელს უშლის He–Ne ლაზერის ასეთი ვიწრო სპექტრული ხაზის რეალიზაციას. ლაზერული დანადგარის ყველა პარამეტრის ზედმიწევნითი სტაბილიზაციის გზით შესაძლებელი გახდა 10–14–10–15 რიგი Δν / ν ფარდობითი სიგანის მიღწევა, რაც დაახლოებით 3-4 რიგით უარესია თეორიულ ზღვართან შედარებით. მაგრამ He–Ne ლაზერის რეალურად მიღწეული მონოქრომატული გამოსხივებაც, რომელსაც ეს ხელსაწყო იძლევა სრულიად შეუცვლელია მრავალი სამეცნიერო და ტექნოკური ამოცანის გადაჭრისას. პირველი He–Ne ლაზერის 1961 წელს შეიქმნა. ნახ. .4-ზე He–Ne ლაზერის გამარტივებული სქემა და ლაზერული გადასვლის ინვერსიული დასახლების მექანიზმია მოცემული.
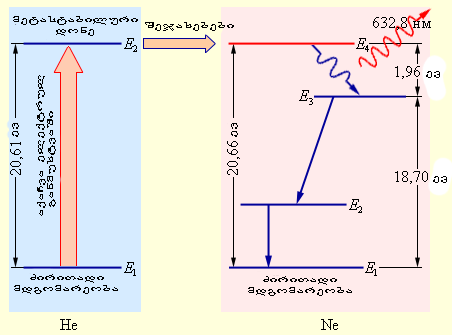
ნახ. 4.
He–Ne ლაზერის გაჯერების მექანიზმი. სწორი ისრებით ატომებში სპონტანური გადასვლებია გამოსახულია
ნეონში E4 → E3 ლაზერული გადასვლის დატუმბვა შემდეგნაირად ხორციელდება. მაღალი ძაბვის ელექტრული განმუხტვისას ელექტრონებთან შეჯახების შედეგად ჰელიუმის ატომების მნიშვნელოვანი ნაწილი გადადის ზედა მეტასტაბილურ E2 დონეზე. ჰელიუმის აღგზნებული ატომები ეჯახებიან ნეონის ძირითად მდგომარეობაში მყოფ ატომებს და გადასცემენ მათ თავიანთ ენერგიას. ნეონის E4 დონე ჰელიუმის მეტასტაბული E2 დონეზე 0,05 ევ-ით მაღლა მდებარეობს. ენერგიის დეფიციტის კომპენსირება ატომენბის დაჯახების კინეტიკური ენერგიის ხარჯზე ხდება. ნეონის E4 დონრეზე ინვერსიული დასახლება იქმნება E3 დონესთან შედარებით, რომელიც ძლიერ ღარიბდება ქვეით განთავსებულ დონეზე სპონტანური გადასვლების ხარჯზე. დატუმბვის საკმარისად მაღალი დონის შემთხვევაში იწყება იდეალურად კოჰერენტული ფოტონების გამრავლების ზვავური პროცესი. თუ აირის ნარევიანი კიუვეტა მოთავსებულია მაღალი არეკვლის უნარის მქონე სარკეებს შორის, იწყება ლაზერული გენერაცია. ნახ. 5-ზე He–Ne ლაზერის ხქემაა მოცემული.

ნახ. 5.
ჰელიუმ-ნეონიანი ლაზერის სქემა: 1 - ჰელიუმისა და ნეონის ნარევიანი მინის კიუვეტა, რომელშიც მაღალი ძაბვის განმუხტვა ხდება; 2 - კათოდი; 3 - ანოდი; 4 - ყრუ სფერული სარკე 0,1 % -ზე ნაკლების გატარებით; 5 - სფერული სარკე 1–2 %-იანი გატარებით
თანამედროვე ჰელიუმ-ნეონიანი ლაზერები მონობლოკიანი მზადდება. ამისათვის მინისებური ნივთიერება, სიტალი გამოიყენება, რომელსაც პრაქტიკულად გაფართოების ნულოვანი ტემპერატურული კოეფიციენტი აქვს. სიტალის მართხკუთხა პარალელოპიპედის ნაჭერში გახვრეტილია არხი რომლის ბოლოებზეც ოპტიკურ კონტაქტზე ემაგრება ლაზერული სარკეები. არხი ივსება ჰელიუმისა და ნეონის ნარევით. კათოდი და ანოდი შეყვანილია დამატებითი გვერდითი არხებიდან. ასეთი ერთბლოკიანი კონსტრუქცია უზრუნვეყოფს მაღალ მექანიკურ და სითბურ სტაბილურობას.
{loadnavigation}
ატომებს შორის უმარტივესი, წყალბადის ატომი ბორის თეორიისათვის თავისებურ ტესტ-ობიექტს წარმოადგენს. თეორიის შექმნის მომენტისთვის ის ექსპერიმენტულად კარგად იყო შესწავლილი. ცნობილი იყო, რომ ის შეიცავს ერთადერთ ელექტრონს. ატომის ბირთვი პროტონია, დადებითად დამუხტული ნაწილაკი, რომლის მუხტი სიდიდით ელექტრონის მუხტის ტოლია, ხოლო მასა 1836-ჯერ აღემათება ელექტრონის მასას.

ჯერ კიდევ XIX საუკუნის დასაწყისში აღმოაჩინეს დისკრეტული სპექტრული ხაზები წყალბადის ატომის გამოსხივების ხილულ სპექტრში (ე.წ. ხაზოვანი სპექტრი). შემდგომში კანონზომიერებები, რომლებიც ხაზოვანი სპექტრის ტალღის სიგრძეები (ან სიხშირეები) ემორჩილება, რაოდენობრივად კარგად იქნა შესწავლილი (ი.ბალმერი, 1885 წ.). წყალბადის ატომის გამოსხივების ხილულ სპექტრში სპექტრული ხაზების ერთობლიობას ბალმერის სერია უწოდეს. მოგვიანებით სპექტრული ხაზების ანალოგიური სერიები აღმოაჩინეს სპექტრის ულტრაიისფერ და ინფრაწითელ ნაწილში. 1890 წელს ი.რიდბერგმა მიიღო ემპირიული ფორმულა სპექტრული ხაზების სიხშირეებისთვის:

ბალმერის სერიისთვის m = 2, n = 3, 4, 5, ... . ულტრაიისფერი სერიისათვის (ლაიმანის სერია) m = 1, n = 2, 3, 4, ... . R მუდმივას რიდბერგის მუდმივა ეწოდება. მისი რიცხვითი მნიშვნელობაა R = 3,29·1015 ჰც. ბორამდე ხაზოვანი სპექტრის წარმოქმნის მექანიზმი და წყალბადის (ან სხვა ატომების) სპექტრული ხაზების ფორმულაში შემავალი მთელი რიცხვების არსი გაუგებარი რჩბოდა.
ბორის პოსტულატებმა განსაზღვრა ახალი მეცნიერების, ატომის ქვანტური ფიზიკის, განვითარება. მაგრამ ისინი არ შეიცავდნენ სტაციონალური მდგომარეობის (ორბიტების) პარამეტრების და მათი შესაბამისი ენერგიის En განსაზღვრის რეცეპტებს.
ბორის მიერ გამოცნობილი იქნა დაქვანტვის წესი, რომელიც ცდებთან თანხმობაში მყოფ წყალბადის ატომის სტაციონალური მდგომარეობების შესაბამის ენერგიებს განსაზღვრავს. მისი შემოთავაზებით, ბირთვის გარშემო მბრუნავი ელექტრონის იმპულსის მომენტს შეუძლია მხოლოდ დისკრეტული მნიშვნელობების მიღება, რომლებიც პლანკის მუდმივას ჯერადი იქნებიან. წრიული ორბიტებისთვის ბორისეული დაქვანტვის წესი შემდეგი სახით ჩაიწერება
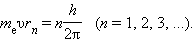
აქ me – ელექტრონის მასაა, υ – მისი სიჩქარე, rn – სტაციონალური წრიული ორბიტის რადიუსია. ბორის დაქვანტვის წესი წყალბადის ატომის ელექტრონის სტაციონალური ორბიტების რადიუსების და მათი შესაბამისი ენერგიების მნიშვნელობების განსაზღვრის საშუალებას იძლევა. ატომბირთვის კულონური ველის რაღაც r რადიუსის მქონე წრიულ ორბიტაზე მბრუნავი ელექტრონის სიჩქარე, ნიუტონის მეორე კანონიდან გამომდინარე, განისაზღვრება თანაფარდობით
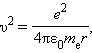
სადაც e – ელექტრონის მუხტია, ε0 – ელექტრული მუდმივა. ელექტრონის სიჩქარე υ და სტაციონალური ორბიტის რადიუსი rn ბორის დაქვანტვის წესით არიან დაკავშირებულნი. აქედან გამომდინარეობს, რომ სტაციონალური ორბიტის რადიუსები განისაზღვრება გამოსახულებით
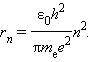
ბირთვთან ყველაზე ახლოს მყოფ ორბიტას შეესაბამება n = 1 მნიშვნელობა. პირველი ორბიტის რადიუსი, რომელსაც ბორის რადიუსად იწოდება, ტოლია

შემდეგი ორბიტების რადიუსები იზრდება n2-ს პროპორციულად.
ატომის ბირთვისა და rn რადიუსის მქონე სტაციონალურ ორბიტაზე მბრუნავი ელექტრონისაგან შედგენილი სისტემის სრული მექანიკური ენერგია ტოლია
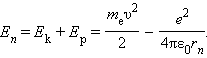
უნდა აღინიშნოს, რომ Ep < 0, რადგანაც ელექტრონსა და ბირთვს შორის მიზიდულობის ძალები მოქმედებს. ამ ფორმულაში υ2 და rn გამოსახულებების ჩასმით მივიღებთ:

მთელ რიცხვებს n = 1, 2, 3, ... ატომის ქვანტურ ფიზიკაში მთავარ ქვანტურ რიცხვებს უწოდებენ.
ბორის მეორე პოსტულატის თანახმად, ელექტრონის En ენერგიის მქონე ერთი სტაციონალური ორბიტიდან მეორე Em < En ენერგიის მქონე სტაციონალური ორბიტაზე გადასვლისას ატომი ასხივებს სინათლის ქვანტს, რომლის სიხშირე νnm ტოლია ΔEnm / h:

ეს ფორმულა ზუსტად ემთხვევა წყალბადის ატომის სპექტრული სერიების რიდბერგის ემპირიულ ფორმულას , თუ R მუდმივას ჩავთვლით

ტოლად.
ამ ფორმულაში me, e, ε0 და h-ს რიცხვითი მნიშვნელობების ჩასმით ვღებულობთ
R = 3,29·1015 ჰც.
რომელიც R -ს ემპირიულ მნიშვნელობასთან ძალიან კარგ თანხმობაშია. ნახ. 1 უჩვენებს წყალდაბის ატომის გამოსხივებისას სპექტრული სერიების წარმოქმნას ელექტრონის უფრო მაღალი სტაციონალური ორბიტიდან უფრო დაბალზე გადასვლისას.
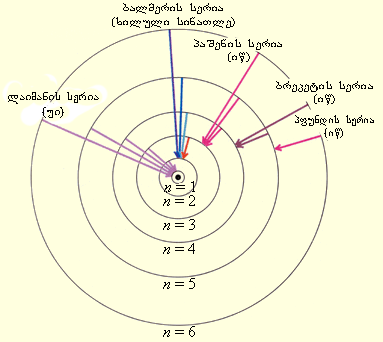
მან. 1.
წყალბადის ატომის სტაციონალური ორბიტები და სპექტრული ხაზების წარმოქმნა
ნახ. 2-ზე გამუსახულია წყალბადის ატომის სტაციონალური ორბიტების დიაგრამა და ნაჩვენებია სხვადასხვა სპექტრული სერიის შესაბამისი გადასვლები.
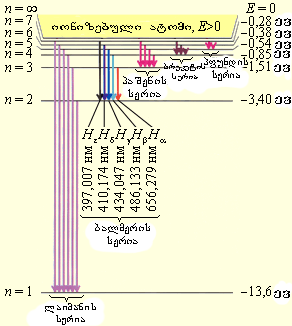
ნახ.2.
წყალბადის ატომის ენერგეტიკული დონეების დიაგრამა. ნაჩვენებია სხვადასხვა სპექტრული სერიის შესაბამისი გადასვლები. მითითებულია სპექტრის ხილული უბნის ბალმერის სერიის პირველი ხუთი ხაზის ტალღის სიგრძეები
წყალბადის ატომისთვის ბორის თეორიის საუკეთესო თანხმობა ექსპერიმენტთან ამ თეორიის სამართლიანობის სასარგებლო წონად არგუმენტს წარმოადგენდა. მაგრამ ამ თეორიის უფრო რთულ ატომებთან მიყენების მცდელობა წარუმატებლად დასრულდა. ბორმა ვერ შესძლო დაქვანტვის წესისთვის ფიზიკური ინტერპრეტაცია მიეცა. ეს ათწლეულით გვიან დე ბროილმა ნაწილაკის ტალღურ ბუნებაზე ცნებების საფუძველზე გააკეთა. დე ბროილის მიხედვით წყალდადის ატომის ყოველი ორბიტა შეესაბამება ტალღას, რომელიც ბირთვის მახლობელ წრეწირზე ვრცელდება. სტაციონალური ორბიტა წარმოიქმნება იმ შემთხვევაში, როცა ტალღა ბირთვის გარშემო ყოველი შემოვლისას უწყვეტად თავის თაცს იმეორებს. სხვა სიტყვებით, სტაციონალური ორბიტა შეესაბამება დე ბროილის წრიულ მდგარ ტალღას ორბიტის ტალღის სიგრძეზე (ნახ. 3). ეს მოვლენა ძალიან ჰგავს ბოლოებით დამაგრებულ სიმში აღძრული მდგარი ტალღის სტაციუნალურ სურათს.
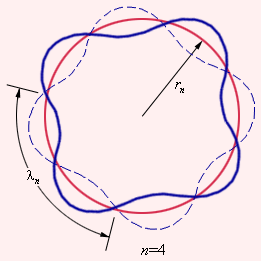
ნახ. 3.
n = 4 შესაბამისი სტაციონალური ორბიტაზე მდგარი ტალღის წარმოქმნის დე ბროილის იდეის ულუსტრაცია
დე ბროილის იდეის მიხედვით წყალბადის ატომის სტაციონალურ ქვანტურ მდგომარეობაში ორბიტის სიგრძეზე უნდა ეტეოდეს ტალღის სიგრძის λ-ს მთელი რიცხვი, ე.ი.
nλn = 2πrn.
ამ თანაფარდობაში დე ბროილის λ = h / p ტალღის სიგრძის ჩასმით, სადაც p = meυ – ელექტრონის იმპულსია, მივიღებთ:
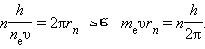
ამგვარად, ბორის დაქვანტვის წესი ელექტრონის ტალღურ თვისებებთანაა დაკავშირებული.
წყალბადის ატომის გამოსხივების სპექტრული კანონზომიერების ახსნაში ბორის თეორიის წარმატება განსაცვიფრებელი იყო. ნათელი გახდა, რომ ატომი ქვანტური სისტემაა, ხოლო ატომის სტაციონალური მდგომარეობების დონეები დისკრეტულია. ბორის თეორიის შექმნასთან ერთად, თითქმის ერთდროულად იქნა მიღებული ატომის სტაციონალური მდგომარეობებისა და ენერგიის დაქვანტვის პირდაპირი ექსპერიმენტული დასაბუთება. ატომის ენერგეტიკული დონეების დისკრეტილობა 1913 წელს იქნა ილუსტრირებული ჯ.ფრანკისად.ფრანკისა და ჰ.ჰერცის იმ ცდის საშუალებით, რომლითაც ვერცხლისწყლის ატომებთან ელექტრონების შეჯახების კვლევა ხდებოდა. აღმოჩნდა, რომ თუ ელექტრონის ენერგია 4,9 ევ-ზე ნაკლებია, მაშინ მათი ვერცხლისწყლის ატომებთან შეჯახება აბსოლუტურად დრეკადი დაჯახების კანონებით ხდება. თუ ენერგია 4,9ევ-ის ტოლია, მაშინ ვერცხლისწყლის ატომებთან შეჯახება არადრეკადი შეჯახების ხასიათს იძენს, ე.ი. ვერცხლისწყლის უძრავ ატომებთან შეჯახებისას ელექტრონები კინეტიკურ ენერგიას სრულად კარგავენ. ეს ნიშნავს, რომ ვერცხლესწყალი შთანთქავს ელექტრონის ენერგიას და ძირითადი მდგომარეობიდან პირველ აღგზნებულ მდგომარეობაში გადადის,
E2 – E1 = 4,9 ევ.
ბორის კონცეფციის თანახმად, უკან თვითნებული გადასვლისას ვერცხლისწყლის ატომი უნდა ასხივებდეს ქვანტს სიხშირით
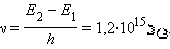
ასეთი სიხშირის სპექტრული ხაზი ვერცხლისწყლის ატომის გამოსხივების სპექტრის ულტრაიისფერ უბანში მართლაც იქნა აღმოჩენილი.
დისკრეტული მდგომარეობების ცნება კლასიკურ ფიზიკას ეწინააღმდეგება. ამიტომაც დაისვა კითხვა, ქვანტური თეორია კლასიკური ფიზიკის კანონებს ხომ არ უარყოფს.
ქვანტურ თეორიას ენერგიის, იმპულსის, ელექტრული მუხტის და სხვ. შენახვის ფუნდამენტური კლასიკური კანონები არ გაუუქმებია. ბორის მიერ ჩამოყალიბებული შესაბამისობის პრინციპის მიხედვით, ქვანტური ფიზიკა მოიცავს კლასიკური ფიზიკის კანონებს, გარკვეულ პირობებში შეინიშნება ქვანტური ცნებებიდან კლასიკურზე მდორე გადასვლა. ამის დანახვა შეიძლება წყალბადის ატომის ენერგეტიკული სპექტრის მაგალითზე (ნახ. 2). დიდი ქვანტრური რიცხვებისას n >>1 დისკრეტული დონეები თანდათანობის უახლოვდებიან ერთმანეთს, და ხდება მდორე გადასვლა უწყვეტი სპექტრის უბანში, რომელიც კლასიკური ფიზიკიდან გამოდის.
ორნაწილიანი, ბორის ნახევრადკლასიკური თეორია ქვანტური წარმოდგენების განვითარების მნიშვნელოვან ეტაპს წარმოადგენდა, რომელთა ფიზიკაში შემოტანამაც მექნიკასა და ელეტროდინამიკაში კარდინალური გარდაქმნები მოითხოვა. ასეთი გადაქმნები XX საუკუნის 20-ან - 30-იან წლებში განხორციელდა.
ბორის წარმოდგენები გარკვეულ ორბიტებზე. რომლებზედაც ელექტრონები მოძრაობდნენ, საკმაორ პირობითი აღმოჩნდა. სინამდვილეში ატომებში ელექტრონების მოძრაობა ძალიან ცოტათი ჰგავს პლანეტების და თანამგზავრების მოძრაობას. ფიზიკური აზრი აქვს ელექტრონის ამა თუ იმ ადგილზე აღმოჩენის ალბათობას, რომელიც ტალღური ფუნქციის კვატრატით |Ψ|2 აღიწერება. ტალღური ფუნქცია Ψ ქვანტური მექანიკის ძირითადი განტოლების, შრედინგერის განტოლების ამოხსნას წარმოადგენს. აღმოჩნდა, რომ ატომში ელექტრონის მდგომარეობა მთელი რიგი ქვანტური რიცხვებით ხასიათდება. მთავარი ქვანტური რიცხვი n ატომის ქვანტურ ენერგიას განსაზღვრავს. იმპულსის მომენტის დაქვანტვისათვის შემოტანილია ე.წ. ორბიტული ქვანტური რიცხვი l. იმპულსის მომენტის გეგმილი სივრცის ნებისმიერ გამოყოფილ მიმართულებაზე (მაგალითად, მაგნიტური ველის \(\vec{B}\) ვექტორის მიმართულება) ასევე მნიშვნელობების დისკრეტულ რიგს იღებს. იმპულსის მომენტის გეგმილის დაქვანტვისათვის შემოტანილია მაგნიტური ქვანტური რიცხვი m. n, l, m ქვანტური რიცხვები დაქვანტვის გარკვეული წესებით არიან დაკავშირებული. მაგალითად, ორბიტული ქვანტური რიცხვი l შეიძლება ღებულობდეს მთელი რიცხვების მნიშვნელობას 0-დან (n – 1)-მდე. მაგნიტური ქვანტური რიცხვი m შეიძლება ღებულობდეს მთელი რიცხვების მნიშვნელობას ±l-ს ინტერვალში. ამგვარად, მთავარი ქვანტური n რიცხვის ყოველ მნიშვნელობას, რომელიც ატომის ენერგეტიკულ მდგომარეობას განსაზღვრავს, l და m ქვანტური რიცხვების კომბინაციების მთელი რიგი შეესაბამება. ყოველ ასეთ კომბინაციას ელექტრონის სივრცის სხვადასხვა წერტილში აღმოჩენის |Ψ|2 ალბათობის გარკვეული განაწილება შეესაბამება („ელექტრული ღრუბელი“).
მდგომარეობა, როცა ორბიტული ქვანტური რიცხვი l = 0-ს, აღიწერება ალბათობების სფერულ სიმეტრიული განაწილებებით. მათ s-მდგომარეობები ეწოდებათ (1s, 2s, ..., ns, ...). როცა l > 0 ელექტრული ღრუბლის სფერული სიმეტრია ირღვევა. l = 1-ს შესაბამის მდგომარეობას p-მდგომარეობას უწოდებენ, l = 2-სას - d-მდგომარეობას და ა.შ.
ნახ. 4-ზე წყალბადის ატომში ელექტრონის ბირთვიდან სხვადასხვა 1s და 2s მანძილებზე აღმოჩენის ρ (r) = 4πr2|Ψ|2 ალბათობის განაწილების მრუდებია გამოსახული.

ნახ. 4.
წყალბადის ატომში ელექტრონის 1s და 2s მდგომარეობებში აღმოჩენის ალბათობის განაწილება. r1 = 5,29·10–11მ - ბორის პირველი ორბიტის რადიუსია
როგორც ნახ. 4-დან ჩანს, 1s მდგომარეობაში (წყალბადის ატომის ძირითადი მდგომარეობა) ელექტრონი შეიძლება ბირთვიდან სხვადასხვა მანძილზე აღმოჩნდეს. უდიდესი ალბათობით შეიძლება აღმოჩნდეს მანძილზე, რომელიც ბორის პირველი ძიროთადი ორბიტის რადიუსს r1-ს ტოლია. 2s მდგომარეობაში ელექტრონის აღმოჩენის ალბათობა მაქსიმალურია ბირთვიდან r = 4r1 მანძილზე. ორივე შემთხვევაში წყალბადის ატომი შიძლება წარმოვიდგინოთ სფერულად სიმეტრიული ელექტრონული ღრუბლის სახით, რომლის ცენტრშიც ბირთვია მოთავსებული.
