იმისათვის, რომ ატომის ბირთვი მდგრადი იყოს, პროტონები და ნეიტრონები ბირთვში უნდა იყვნენ დაკავშირებული ერთმანეთთან უზარმაზარი ძალებით, ღომლებიც მრავალჯერ აღემატება პროტონების ურთიერთგანზიდვის ძალებს. ბირთვში ნუკლონების შემაკავებელ ძალებს ატომურს უწოდებენ. ისინი წარმოადგენენ ფიზიკაში ცნობილ ურთიერთქმედებათა შორის ყველაზე ინტენსიურს, ე.წ ძლიერ ურთიერთქმედებას. ატომური ძალები დაახლოებით 100-ჯერ აღემატება ელექტრულ ძალებს და ათეული რიგით აღემატება ნუკლონების გრავიტაციულ ურთიერთქმედებას. ატომური ძალების მნიშვნელოვან თავისებურებას წარმოადგენს მათი ახლომოქმედების ხასიათი. ატომური ძალები შესამჩნევად იჩენს თავს, როგორც რეზერფორდის α-ნაწილაკების გაბნევის ცდები უჩვენებენ, მხოლოდ ბირთვის ზომების რიგის (10–12–10–13 სმ) მანძილებზე. დიდ მანძილებზე თავს იჩენს შედარებად ნელად კლებადი კულონის ძალები.
ექსპერიმენტულ ფაქტებზე დაყრდნობით შეიძლება დავასკვნათ, რომ ბირთვში პროტონები და ნეიტრონები ძლიერი ურთიერთქმედების მიმართ ერთნაირად იქცევიან, ე.ი. ატომური ძალები არ არის დამოკიდებული ნაწილაკის მატარებელია თუ არა.
ატომურ ფიზიკაში უმნიშვნელოვანეს როლს ბირთვის ბმის ენერგიის ცნება ასრულებს.
ბირთვის ბმის ენერგია იმ მინიმალური ენერგიის ტოლია, რომელიც საჭიროა ატომის ცალკეულ ნაწილაკებად სრული დაშლისათვის. ენერგიის შენახვის კანონის მიხედვით, ბმის ენერგია ტოლია იმ ენერგიისა, რომელიც გამოიყოფა ცალკეული მაწილაკებისაგან ბირთვის შექმნის შემთხვევაში.
ნებისმიერი ბირთვის ბმის ენერგია მისი მასის ზუსტი გაზომვით შეიძლება განისაზღვროს. დღეისთვის ფიზიკოსებს შეუძლიათ გაზომონ მაწილაკების, ელექტრონის, პროტონის, ნეიტრონის, ბირთვის და ა.შ. მასები, ძალიან დიდი სიზუსტით. ეს გაზომვები უჩვენებენ, რომ ნებისმიერი ბირთვის Mბ მასა ყოველთვის ნაკლებია მასში შემავალი პროტონეისა და ნეიტრონების მასათა ჯამზე:
Mя < Zmp + Nmn.
მასათა სხვაობას
ΔM = Zmp + Nmn – Mя.
მასის დეფექტს უწოდებენ.
მასის დეფექტის მიხედვით ეინშტეინის ფორმულის E = mc2 საშუალებით შეიძლება განისაზღვროს ენეგია, რომელიც მოცემული ბირთვის წარმოქმნისას გამოიყოფა, ე.ი. ბირთვის ბმის Eბმ ენერგია:
Eсв = ΔMc2 = (Zmp + Nmn – Mя)c2.
ბირთვის წარმოქმნისას ეს ენერგია γ-ქვანტების სახით გამოსხივდება.
მაგალითისათვის გამოვთვალოთ ბმის ენერგია ჰელიუმის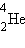 
ბირთვისათბვის, რომლის შემადგენლობაშიც შედის ორი პროტონი და ორი ნეიტრონი. ჰელიუმის ბირთვის მასა Mя = 4,00260 მ.ა.ე.-ა. ორი პროტონის და ორი ნეიტრონის მასა შეადგენს 2mp + 2mn = 4, 03298 მ.ა.ე-ს. აქედან გამომდინარე, ჰელიუმის ბირთვის მასის დეფექტი ტოლია ΔM = 0,03038 მ.ა.ე-სი. Eсв = ΔMc2 ფორმულით გათვლას მივყავართ 
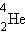ჰელიუმის ბირთვის ბმის ენერგიის შემდეგ მნიშვნელობამდე: Eсв = 28,3 მევ. ეს უზარმაზარი ენერგიაა. მხოლოდ 1 გ ჰელიუმის წარმოქმნას თან ახლავს 1012 ჯ-ს რიგის ენერგიის გამონთავისუფლება. დაახლოებით იმდენივე ენერგია გამოიყოფა თითქმის მთელი ვაგონი ქვანახშირის დაწვის შედეგად. ატომის ბირთვის ბმის ენერგია მრავალი რიგით აჭარბებს ელექტრონის ატომთან ბმის ებერგიას. მაგალითად, წყალბადის 
ატომისათვის იონიზაციის ენერგია 12,6 ებ-ს ტოლია.
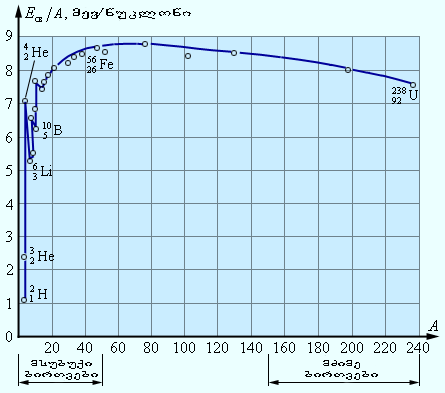
ცხრილებში მოიცემა ბმის კუთრი ენერგია, ე.ი. ბმის ენერგია ერთი ნუკლონისათვის. ჰელიუმის ბირთვისთვის ბმის კუთრი ენერგია დაახლოებით ტოლია 7,1 მევ/ნუკლონი. ნახ. 1-ზე მბის კუთრი ენერგიის A მასურ რიცხვზე დამოკიდებულების გრაფიკია მოცემული. როგორც გრაფიკიდან ჩანს, ნუკლონების ბმის კუთრი ენერგია სხვადსხვა ატომის ბირთვისთვის ერთნაირი არაა. მსუბუქი ბირთვებისთვის ბმის კუთრი ენერგია თავიდან მკვეთრად იზრდება 1,1 მევ/ნუკლონიდან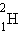 
დეიტერიუმისათვის, 7,1 მევ/ნუკლონამდე 
ჰელიუმისათვის. შემდეგ, რიგი ნახტომების გავლით, ბმის კუთრი ენერგია იზრდება მაქსიმალურ 8,7 მევ/ნუკლონ მნიშვნელობამდე A = 50–60 მასური რიცხვის მქონე ელემენტებისათვის, შემდეგ მძიმე ელემენტებისათვის შედარებით ნელა კლებულობს. მაგალითად,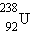 
ურანისათვის ის 7,6 მევ/ნუკლონს აღწევს.
ნახ.1.
ბირთვების ბმის კუთრი ენერგია
მძიმე ელემენტებზე გადასვლისას ბირთვების ბმის კუთრი ენერგიის შემცირება პროტონების კულონური განზიდვის ენერგიის გაზრდით აიხსნება. მძიმე ბირთვებში ნუკლონებს შორის კავშირი სუსტდება, ხოლო თითონ ბირთვები ნაკლებად მდგარადი ხდება.
სტაბულური მსუბუქი ბირთვების შემთხვევაში, სადაც ნუკლონების ურთიერთქმედება დიდი არაა, პროტონების და ნეიტრონების Z და N რიცხვი ერთნაირია (
, 
, 
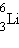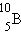). ატომური ძალების მოქმედებით იქმნება პროტონ-ნეიტრონული წყვილები. მაგრამ მძიმე ელემენტების ბირთვებს, რომლებშიც პროტონების დიდი რიცხვია, კულონური განზიდვის ენერგიის ზრდის გამო მდგრადობის გაზრდისთვის დამატებითი ნეიტრონები ესაჭიროებათ. ნახ. 2-ზე მოყვანილია დიაგრამა, რომელიც პროტონისა და ნეიტრონების რიცხვს უჩვენებს სტაბილურ ბირთვებში. ბირთვებისთვის, რომლებიც ბისმუტს (Z > 83) მოჰყვებიან, პროტონების დიდი რიცხვის გამო სრული სტაბილურობა შეუძლებელი ხდება.
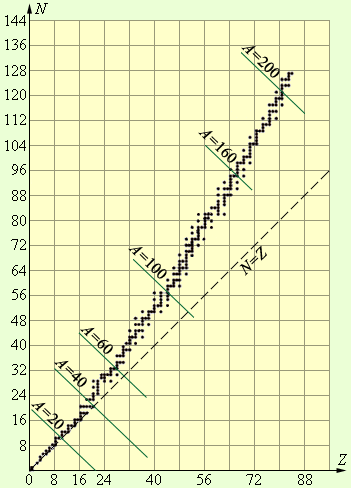
ნახ. 2.
პროტონებისა და ნეიტრონების რიცხვი სტაბილურ ბირთვებში
ნახ.1-დან ჩანს, რომ ენერგეტიკული თვალსაზრისით ყველაზე სტაბილურს წარმოადგენენ მენდელეევის სისტემის შუა ნაწილის ელემენტების ბირთვები. ეს ნიშნავს, რომ ბირთვული გარდაქმნებისას არსებობს დადებითი ენერგიის გამომუშავების ორი შეასაძლებლობა:
1. მძიმე ბირთვების დაყოფა უფრო მსუბუქ ბირთვებად;
2. მსუბუქი ბირთვების შერწმით უფრო მძიმე ბირთვის წარმოქმნა.
ორივე პროცესში ენერგიის უზარმაზარი რაოდენობა გამოიყოფა. დღეისათვის ორივე პროცესი პრაქტიკულადაა განხორციელებული: დაშლის რეაქცია და თერმობირთვული რეაქცია.
შევასრულოთ გარკვეული შეფასება. ვთქვათ, მაგალითად, ურანის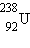 
ბირთვი იყოფა ორ ერთნაირ ბირთვად მასური რიცხვით 119. ამ ბირთვების, როგორც ჩანს ნახ.1-დან, ბმის კუთრი ენერგია 8,5 მევ/ნუკლონზე რიგისაა. ურანის ბირთვის ბმის კუთრი ენერგია 7,6 მევ/ნუკლონზეა. აქედან გამომდინარე, ურანის ბირთვის გაყოფისას გამოყოფილი ენერგია ტოლია 0,9 მევ/ნუკლონზეა ან 200 მევ ურანის ერთ ატომზე.
ახლა მეორე პროცესი განვიხილოთ. ვთქვათ გარკვეულ პირობებში დეიტერიუმ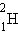 
ორი ბირთვის შერწყმით 
ჰელიუმის ერთი ბირთი წარმოიქმნა. დეიტერიუმის ბირთვების ბმის კუთრი ენერგია ტოლია 1,1 მევ/ნუკლონზე, ხოლო ჰელიუმის ბირთვების ბმის კუთრი ენერგია 7,1 მევ/ნუკლონზე. აქედან გამომდინარე, დეიტერიუმის ორი ბირთვისაგან ჰელიუმის ერთი ბირთვის სინთეზისას გამოყოფილი ენერგია ტოლია 6 მევ/ნუკლონზე ან 24 მევ ჰელიუმის ერთ ატომზე.
ყურადღება უნდა მიექცეს იმას, რომ მსუბუქი ბირთვების სინთეზისას მძიმე ბირთვების გაყოფასთან შედარებით 6-ჯერ უფრო დიდი ენერგია გამოიყოფა ყოველ ერთ ნუკლონზე.