პრაქტიკაში განსაკუთრებით საინტერესოა სინათლის დიფრაქციის შემთხვევა, როცა წინააღმდეგობა ღიად ფრენელის პირველი ზონის მხოლოდ მცირე ნაწილს ტოვებს. ამ შემთხვევას ადგილი აქვს თუ სრულდება პირობები
ანუ ამ შემთხვევაში დიფრაქციული სურათი მცირე ზომის წინააღმდეგობიდან ძალიან დიდი მანძილზე უნდა დაიკვირვებოდეს. მაგალითად, თუ R = 1 მმ, λ = 550 ნმ (მწვანე სინათლე), მაშინ დაკვირვების სიბრტყემდე L მანძილი 2 მ-ს მნიშვნელოვნად უნდა აღემატებოდეს (ე.ი. მინიმუმ 10მ ან მეტი). ტალღის ფრონტის სხვადასხვა ელემენტებიდან დაკვირვების შორეულ წერტილამდე გავლებული სხივები შეიძლება პარალელურად ჩაითვალოს. დიფრაქციის ამ შემთხვევას სწორად ასე უწოდებენ - პარალელური სხივების დიფრაქცია ან ფრაუნჰოფერის დიფრაქცია - გერმანელი ფიზიკოსის ი.ფრაუნჰოფერის საპატივცემლოდ, რომელიც ფრენელის თანამედროვე იყო. თუ სხივების გზაზე წინააღმდეგობის შემდეგ შემკრებ ლინზას მოვათავსებთ, პარალელურ სხივთა კონა, რომელმაც დიფრაქცია განიცადა წინააღმდეგობაზე, რაღაც θ კუთხით თავს მოიყრის ფოკალური სიბრტყის რაღაც წერტილში (ნახ. 1). აედან გამომდინარე, ლინზის ფოკალური სიბრტყის ნებისმიერი წერტილი ექვივალენტურია ლინზის გარეშე უასასრულოდ დაშორებული წერტილისა.
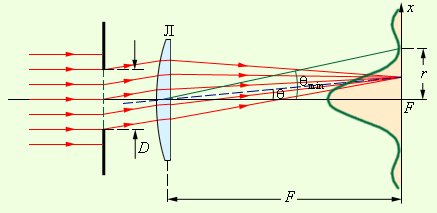
ნახ. 1.
პარალელური სხივების დიფრაქცია. მწვანე მრუდი -ინტენსივობების განაწილება ფოკალურ სიბრტყეში (ღერძის მასშტაბი ძალიან გაზრდილია)
ლინზის ფოკალურ სიბრტყეში ფრაუნჰოფერის დიფრაქციული სურათი დაიკვირვება. მაგრამ, გეომეტრული ოპტიკის თანახმად, ლინზის ფოკუსში შორეული საგნის წერტილოვანი გამოსახულენა უნდა მიიღებოდეს. მაგრამ სინამდვილში წერტილოვანი საგნის გამოსახულება დიფრაქციის გამო იდღაბნება. ამაში ვლინდება სინათლის ტალღური ბუნება.
არანაირ ოპტიკურ სისტემას წერტილოვანი გამოსახულების მოცემა არ შეუძლია. ფრაუნჰოფერის დიფრაქციის შემთხვევაში D დიამეტრის მრგვალ ხვრელზე დიფრაქციული გამოსახულება შედგება მხოლოდ ცენტრალური ნათელი ლაქისგან (ეირის დისკი), რომელზეც სინათლის ენერგიის თითქმის 85% მოდის, და მისი გარემომცველი ნათელი და ბნელი ზოლებისაგან (ნახ. 2). სწორედ ეს დიფრაქციული ლაქა ითვლება წერტილოვანი წყაროს გამოსახულებად. ცენტრალური ლაქის რადიუსი ლინზის ფოკალურ სიბრტყეზე ტოლია
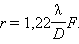
თუ დაშორებილი წყაროდან სინათლის სხივი ეცემა პირდაპირ ლინზას, მაშინ იმ ეკრანის როლს, რომელზედას სინათლე განიცდის დიფრაქციას, ლინზის ჩარჩო ასრულებს. ამ შემთხვევაში D -ში ლინზის დიამეტრი იგულისხმება.
ნახ.2.
წერტილოვანი წყაროს დიფრაქციული გამოსახულება (დიფრაქცია მრგვალ ხვრელზე). ცენტრალურ ლაქაზე სინათლის ენერგიის თითქმის 85% მოდის
დიფრაქციული გამოსახულების ზომა ძალიან მცირეა. მაგალითად, D = 5 სმ დიამეტრისა და F = 50 სმ ფოკუსური მანძილის მქონე ლინზის λ = 500 ნმ ტალღის სიგრძის მონოქრომატული სინათლისთვის ფოკალურ სიბრტყეში ცენტრალური ნათელი ლაქის რადიუსი 0,006 მმ-ს ტოლია. ბევრ ოპტიკურ მოწყობილობაში (ფოტოაპარატი, პროექტორი და სხვა) გამოსახულების დიფრაქციული გადღაბნა ინიღბება ოპტიკის არასრულყოფილებით გამოწვეული გაცილებით უფრო ძლიერი დამახინჯებით.
მაგრამ მაღალი ხარისხის ასტრონომიულ ხელსაწყოებში გამოსახულიბის ხარისხის დიფრაქციული ზღვარი ხორციელდება. ობიექტის ორი ახლომდებარე წერტილის გამოსახულება დიფრაქციული გადღაბნის შედეგად შეიძლება ვერ გაირჩეს ერთი წერტილისაგან (ერთმანეთისაგან). მაგალითის სახით განვიხილოთ შემთხვევა, როცა ასტრონომიული ტელესკოპის ობიექტივი მიმართულია ორი ახლომდებარე ვარსკვალვისაკენ, ერთმანეთისაგან ψ კუთხურ მანძილზე. იგულისხმება, რომ ყველა დეფექტი და აბერაცია მოშორებულია, და ობიექტივის ფოკალურ სიბრტყეში დაიკვირვება ვარსკვლავების დიფრაქციული გამოსახულება (ნახ. 3).
ნახ. 3.
ორი ახლომდებარე ვარსკვლავის დიფრაქციული გამოსახულება ტელესკოპოს ობიექტივის ფოკალურ სიბრტყეში
ნახ. 3-ზე ვარსკვლავების დიფრაქციულ გამოსახულებათა ცენტრებს შორის Δl მანძილი აჭარბებს ცენტრალუტი ნათელი ლაქის r რადიუსს - ამ შემთხვევაში ვარსკვალვების გამოსახულებები დამკვირვებლის მიერ ცალ-ცალკე აღიქმება და, ე.ი. ტელესკოპის ობიექტივი ორი ახლომდებარე ვაესკვალავის გარჩევის საშუალებას იძლევა. ვარსკვლავებს შორის ψ კუთხური გარჩევის შემცირების შემთხვევაში დიფრაქციოლ გამოსახულებებს შეუძლიათ ძლიერად გადაფარონ ერთმანეთი და არ განირჩევიან ერთი ვარსკვლავის გამოსახილებისაგან. ამ შემთხვევაში ტელესკოპის ობიექტივი ვერ არჩევს ახლომდებარე ვარსკვლავებს. XIX საუკუნის ბოლოს ინგლისელმა ფიზიკოსმა რელეიმ წამოაყენა პირობა, რომ გარჩევა ჩაითვალოს სრულად, თუ გამოსახულების ცენტრებს შორის Δl მანძილი ტოლია (ან აჭარბებს) ეირის დისკის r რადიუსს (ნახ. 3.9.4). პირობას Δl = r გარჩევის რელეის კრიტერიუმს უწოდებენ. ამ კრიტერიუმიდან გამოდის:
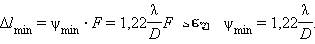
D = 1 მ დიამეტრია ტოლი ობიექტივის მქონე ტელესკოპს შეუძლია გაარჩიოს ორი ვარსკვალავი, რომლების ერთმანეთისაგან ψmin = 6,7·10–7 რად კუთხურ მანძილზე მდებარეობენ (λ = 550 ნმ-სათვის) .
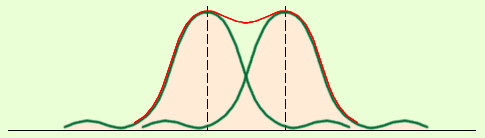
ნახ. 4.
რელეის გარჩევის უნარი. წითელი მრუდი - სინათლის ჯამური ინტენსივობის განაწილება
ორბიტაზე 1990 წელს გაყვანილი ჰაბლის კოსმოსური ტელესკოპის სარკის დიამეტრია D = 2,40 მ. ამ ტელესკოპის ზღვრული კუთხური გარჩევა λ = 550 ნმ ტალღის სიგრძეზე ტოლია: ψmin = 2,8·10–7 რად. ტელესკოპის მუშაობაზე გავლენას არ ახდევს ატმოსფერული შეშფოთებები. ტელესკოპის ობიექტივის დასახასიათებლად შეიძლება ზღვრული კუთხური გარჩევის ψmin შებრუნებული სიდიდის R-ს შემოტანა. ამ სიდიდეს ტელესკოპის გარჩევის უნარს უწოდებენ:
ტელესკოპის გარჩევის უნარის გასაზრდელად უნდა გაიზარდოს ობიექტივის დიამეტრი (ან გამოყენებული უნდა იქნეს უფრო მოკლე ტალღები). ყველაფერი რაც ზემოთ ითქვა ტელესკოპისათვის შეუიარაღებელი თვალისათვისაც სამართლიანია. დაშორებული საგნის დათვალიერებისას თვალი ისევე მოქმედებს როგორც ტელესკოპის ობიექტივი. D -ს როლს გუგის დიამეტრი dმზ ასრულებს. ჩავთვალოთ, რომ dმზ = 3 მმ, λ = 550 ნმ და ვიპოვოთ თვალის გარჩევის ზღვრული კუთხე
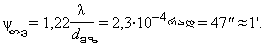
ეს შეფასება კარგ თანხმობაშია თვალის გარჩევის უნარის ფიზიოლოგიურ შეფასებასთან, რომელიც ბადურის სინათლის მგრძნობიარე ელემენტების (ჩხირების და კოლბების) ზომებიდან გამომდინარე მიიღება.
ახლა შეიძლება ერთი საერთო დასკვნის გაკეთება: D დიამეტრისა და λ ტალღის სიგრძის სინათლის კონა სინათლის ტალღური ბუნებიდან გამომდინარე განიცდის დიფრაქციულ გაფართოებას. კონის კუთხური ნახევარსიგანე φ λ / D რიგისაა. ასე რომ, სრული d სიგანე L მანძილზე დაახლოებით ტოლია
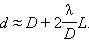
ნახ. 5-ზე ნაჩვენებია, წინააღმდეგობიდან დაშორებით თუ როგორ ტრანსფორმირდება სინათლის კონა.
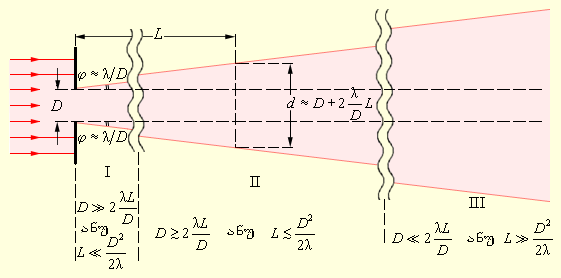
ნახ. 5.
დიფრაქციის გავლენით გაფართოებული სინათლის კონა. I არე – სინათლის სხივის ცნება, გეომეტრული ოპრიკის კანონები. I I არე – ფრენელის ზონები,პუასონოს ლაქა. I I I არე – პარალელური სხივების დიფრაქცია
ნახ. 5-ზე მოყვანილი შეფასებები უჩვენებენ, რომ კონის კუთხური გაშლა მცირდება მისი საწყისი D დიამეტრის ზომის ზრდით. ეს დასკვნა სამართლიანია ნებისმიერი ბუნების ტალღებისთვის. მაგალითად, რომ გავუშვათ ლაზერის გამოსხივების „ვიწრი“ კონა მთვარეზე, ჯერ მისი გაფართოებაა საჭირო. ეს ტელესლოპის საშუალებით მიიღწევა: ლაზერის კონა შედის ოკულარში, გაივლის ტელესკოპის მილს და ობიექტივიდან D დიამეტრის მქონე გამოდის (ნახ. 6).
ნახ. 6.
ლაზერული სხივთა კონის გაფართოება ტელესკოპური სისტემის საშუალებით
ასეთი გაფართოებული კონა მთვარეზე მისვლის მერე, მასზე „გაანათებს“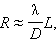 
რადიუსის ტოლ ლაქას, სადაც L – მთვარემდე მანძილია. თუ D = 2,5 მ , λ = 550 ნმ, L = 4·106 მ, მაშინ მივიღებთ R ≈ 90 მ. მთვარეზე ლაზერული სინათლის საწყისი კონა რომ გაგვეშვა, რომლის დიამედრია 1სმ, მაშინ მთვარეზე განათებული ფართობი 250-ჯერ დიდი იქნებოდა.
მიკროსკოპის გარჩევის უნარი. მიკროსკოპის საშუალებით ახლომდებარე სხეულები დაიკვირვება, ამიტომ მისი გარჩევის უნარი ხასიათდება არა ორ მახლობელი წერტილს შორის კუთხური, არამედ წრფივი მანძილით, რომლის დროსაც ეს წერტილები კერ კიდევ ცალცალკე დაიკვირვებიან. დასაკვირვებელი ობიექტი ობიექტივის წინა ფოკუსში თავსდება. ხშირად ობიექტივის წინა სივრცე სპეციალური გამჭვირვალე სითხით - იმერსიით - ივსება (ნახ. 7). სიბრტყეში, რომელიც გეომეტრიულად ობიექტთანაა დაკავშირებული, თვალის მიერ ოკულარში დაკვირვებული გადიდებული გამოსახულება თავსდება. ყოველი წერტილის გამოსახულება გადღაბნილია დიფრაქციის შედეგად.
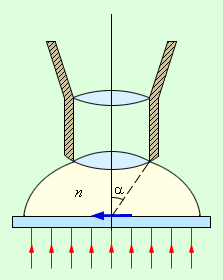
ნახ. 7.
იმერსიული სითხე მიკრისკოპის ობიექტივის წინ
მიკროსკოპის გარჩევის უნარის ზღვარი პირველად გერმანელმა ფიზიკოსმა ჰელმჰოლცმა განსაზღვრა, ჰელჰოლცის ფორმულას აქვს სახე:
სადაც λ – ტალღის სიგრძეა, n – იმერსიული სითხის გარდატეხის კოეფიციენტი, α – ე.წ. აპერურული კუთხე (ნახ. 3.9.7). n sin α სიდიდეს რიცხვითი აპერტურა ეწოდება.
კარ მიკრისკოპებში აპერტურილი კუთხე α მისი ზღვის ტოლია: α ≈ π / 2. როგორც ჰენჰოლცის ფომულიდან ჩანს, იმერსიის გამოყენებით გარჩევის ზღვარი გარკვეულად იზრდება. როცა α ≈ 1, n ≈ 1,5, მივიღებთ:
lmin ≈ 0,4 λ.
ამგვარად, მიკრისკოპის საშუალებით პრინციპულად შეუძლებელია ისეთი დეტალის დათვალიერება, რომლის ზომებიც სინათლის ტალღის სიგრძეზე ნმიშვნელოვნად ნაკლებია. სინათლის ტალღური თვისებები განსაზღვრავენ, ნებისმიერი ოპტიკური სისტემით მიღებული, ობიექტის გამოსახულების ხარისხს.