ხილული სინათლე შედგება სხვადასხვა ტალღის სიგრძის მონოქრომატული ტალღებისაგამ. გახურებული სხეულების გამოსხივებაში (ვარვარების ნათურის ძაფი) ტალღის სიგრძეები უწყვეტად ავსებენ სინათლის მთელ დიაპაზონს. ასეთ გამოსხივებას თეთრ სინათლეს უწოდებენ. სინათლე, რომელსაც, მაგალითად, აერის განმუხტვის ნათურები და ბევრი სხვა წყარო ასხივებს, მის შემადგენლობაში შეიცავს ცალკეულ მონოქრომატულ მდგენელს ტალღის სიგრძეების გამოყოფილი მნიშვნელობებით. გამოსხივებაში მონიქრომატული კომპონენტების ერთობლიობას სპექტრს უწოდებენ. თეთრ სინათლეს იწყვეტი სპექტრი აქვს. ისეთი წყაროს გამოსხივებას, რომელშიც სინათლეს ნივთიერების ატომები ასხივებენ, დისკრეტული სპექტრი აქვს. ხელსაწყოები, რომლის საშუალებითაც გამოსხივების წყაროები სპექტრების შეისწავლება, სპექტრულ ხელსაწყოებს უწოდებენ.
გამოსხივების სპექტრად დასაშლელად უმარტივეს სპექტრულ ხელსაწყოში პრიზმა გამოიყენება (ნახ. 1). პრიზმის მოქმედება დამყარებულია დისპერსიის მოვლენაზე, ანუ ნივთიერების n გარდატეხის უნარის სინათლის λ ტალღის სიგრძეზე დამოკიდებულებაზე.
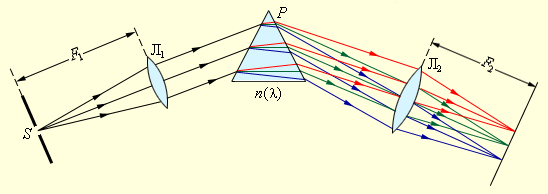
ნახ. 1.
გამოსხივების სპექტრად დაშლა პრიზმის საშუალებით
S ჭვრიტე, რომელსაც ეცემა გამოსაკვლეევი გამოსხივება, Л1 ლინზის ფოკალურ სიბრტყეში მდებარეობს. ხელსაწყოს ამ ნაწილს კოლიმატორს უწოდებენ. ლინზიდან გამოსული სინათლის პარალელურ სხივთა კონა P პრიზმას ეცემა. დისპერსიის შედეგად სხვდასხვა ტალღის სიგრძის მქონე სინათლე პრიზმიდან სხვადასხვა კუთხით გამოდის. Л2 ლინზის ფოკალურ სიბრტყეში მოთავსებულია ეკრანი ან ფოტოფირფიტა, რომელზედაც გამოსახულება მიიღება. ამის შედეგად ეკრანის სხვადასხვა ადგილებში წარმოიქმნება ჭვრიტის მსგავსი სხვადასხვა ტალღის სიგრძის გამოსახულებები. ყველა გამჭვირვალე მყარ სხეულებს (მინას. კვარცს), რომლისგანაც პრიზმები მზადდება, ხილული სინათლის დიაპაზონში n გარდატეხის მაჩვენებელი λ ტალღის სიგრძის ზრდასთან ერთად მცირდება, ამიტომაც პრიზმა საწყისი მიმართულებიდან ყველაზე მეტად ლურჯ და იისფერ სხივებს გადახრის, ყველაზე ნაკლებად კი - წითელს. მონოტონურად კლებად n (λ) დამოკიდებულებას ნორმალურ დისპერსიას უწოდებენ.
თეთრი სინათლის სპექტრად დაშლის პირველი ცდა ნიუტონმა განახორციელა (1672 წ.).
მაღალი კლასის სპექტრულ ხელსაწტოებში პრიზმის ნაცვლად დიფრაქციულ მესერს იყენებენ. მესერი მინის ან მეტალურ ზედაპირზე, სპეციალური დამყოფი მანქანით ამოგრავირებული, პერიოდულ სტრუქტურას წარმოადგენს (ნახ. 3.10.2). კარგ მესერებს ერთმანეთის პარალელური შტრიხები 10 სმ-ია, ხოლო ყოველ მილიმეტრზე 2000 შტრიხამდეა. ამასთან მესერის საერთო სიგრზე 10-15 სმ-ს აღწევს. ასეთი მესერის დასამზადებლად ყველაზე მაღალი ტექნოლოგიაა საჭირო. პრაქტიკაში უფრო უხეში, გამჭვირვალე აფსკზე დატანილი 50-100 შტრიხი მილიმეტრზე, მესერებიც გამოიყენება. დიფრაქციულ მესერად კონპაქტ-დისკის ან ძველი გრამაფონის ფირფიტის ნაწილიც შეიძლება იქნეს გამოყენებული.
ნახ. 2.
დიფრაქციული მესერი
უმარტივესი დიფრაქციული მესერი შედგება გამჭვირვალე უბნებისა (ჭვრიტეები), რომლებიც გაუმჭვირვალე შვუალუდებითაა გაყოფილი. მესერზე კოლიმატორის საშუალებით მიმართულია გამოსაკვლევი სინათლის პარალელურ სხივთა კონა. დაკვირვება მესერის უკან მოთავსებული ლინზის ფოკალურ სიბრტყეში ხვდება (ნახ. 3).
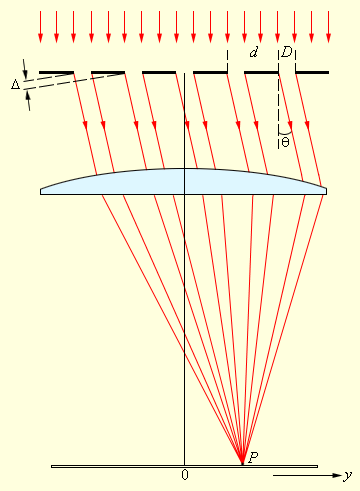
ნახ. 3.
დიფრაქციული სინათლე მესერზე
ლინზის ფოკალურ სიბრტყეში მოთავსებული ეკრანის ყოველ P წერტილში შეიკრიბება სხივები, რომლებიც ლინზამდე ერთმანეთის პარალელურები იყვნენ და დაცემული ტალღის მიმართულებით გარკვეული θ კუთხით ვრცელდებოდნენ. რხევები P წერტილში სხვადასხვა ჭვრიტეებიდან მოსული მეორადი ტალღების ინტერფერენციის შედეგს წარმოადგენს. იმისათვის, რომ P წერტილში დაიკვირვებოდეს ინტერფერენციული მაქსიმუმი, მეზობელი ჭვრიტეებიდან გამოსული ტალღებს შორის სვლათა სხვაობა Δ ტალღის სიგრძის მთელი რიცხვის ტოლი უნდა იყოს:
Δ = d sin θm = mλ (m = 0, ±1, ±2, ...).
აქ d – მესერის პერიოდი, m –მთელი რიცხვი, რომელსაც დიფრაქციული რიგის მაქსიმუმს უწოდებენ. ეკრანის იმ წერტილებში, რომლებშიც ეს პირობა სრულდება, განთავსებულია ე.წ. დიფრაქციული სურათის მთავარი მაქსიმუმები.
ლინზის ფოკალურ სიბრტყეში ნულოვანი რიგის (m = 0) მაქსიმუმიდან m -ური რიგის მაქსიმუმამდე მანძილი დიფრაქციის მცირე კუთხის შემთხვევაში ტოლია

სადაც F – ფოკუსური მანძილია.
ყრადღება მისაქცევია, რომ ლინზის ფოკალური სიბრტყის ყოველ წერტილში მესერის N ჭვრიტიდან მოსული N ტალღის ინტერფერენცია ხდება.ეს ე.წ. მრავალტალღოვანი (ან“მრავალსხივიანი“) ინტერფერენციაა. დაკვირვების სიბრტყეში სინთლის ენერგიის განაწილება მკვეთრად განსხვავდება იმისაგან, რასაც ჩვეულებრივი „ორსხივიან“ ინტერფერენციულ სქემაში აქვს ადგილი. მთავარ მაქსიმუმებში ყველა ტალღა ფაზაში მიდის, ამიტომ რხევის ამპლიტუდა N -ჯერ იზრდება, ხოლო ინტენსივობა N2-ჯერ იმ რხევასთან შედარებით, რასაც ერთი ჭვრიტიდან მომავალი ტალღა აღძრავს.
შერევისას მთავარი მაქსიმუმებიდან რხევის ინტენსივობა სწრაფად ეცემა. N ტალღამ რომ ერთმანეთი ჩააქროს, ფაზათა სხვაობა უნდა შეიცვალოს 2π / N-თი, და არა π -თი, ისე როგორც ორი ტალღის ინტერფერენციისას. ნახ. 4-ზე მოცემულია ვექტორული დიაგრამა რხევებისა, რომელიც ყველა N ჭვრიტიდან აღიძვრება იმ პირობით, რომ მეზობელ ჭვრიტეებს შორის ფაზათა სხვაობა ტოლია 2π / N, და შესაბამისად სვლათა სხვაობა ტოლია λ / N. N რხევის გამომსახველი ვექტორი ამ შემთხვევაში ჩაკეტილი მრავალკუთხედით გამოისახება. ამგვარად, მთავარი მაქსიმუმიდან მეზობელ მინიმუმში გადასვლისას სვლათა სხვაობა Δ = d sin θ უნდა შეიცვალოს λ / N -თი. ამ პირობიდან შეიძლება შეფასდეს მთავარი მაქსიმუმების კუთხური ნარევარსიგანე δθ:

აქ სიმარტივისათვის იგულისხმება, რომ დიფრაქციული კუთხე საკმარისად მცირეა. აქდან გამომდინარე,
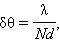
სადაც Nd – მესერის სრული ზომებია. ეს თანაფარდობა სრულ თანხმობაშია პარალელური სხივების დიფრაქციის თეორიასთან, რომლის მიხედვითაც პარალელურ სხივთა კონის დიფრაქციული განშლა ტოლია ტალღის სიგრძის ფარდობისა წინააღმდეგობის განივ ზომასთან.

ნახ. 4.
ინტერფერენციული სურათში რხევის შეკრება მაქსიმუმსა და მინიმუმში: a –ორი ტალღის ინტერფერენცია; b – N ტალღის ინტერფერენცია (N=8)
შესაძლებელია მნიშვნელოვანი დასკვნის გაკეთება: მესერზე სინათლის დიფრაქციისას მთავარი მაქსიმუმები ძალიან ვიწროებია. ნახ. 5 იძლევა წარმოდგენას თუ როგორ იცვლება მთავარი მაქსიმუმების სივიწროვე მესერის ჭვრიტეების რიცხვის გაზრდით.

ნახ. 5.
ინტენსივობის განაწილემა ჭვრიტეების სხვადასხვა რიცხვის მქონე მესერებზე მონოქრომატული სინათლის დიფრაქციის შემთხვევაში. I0 – ერთ ჭვრიტეზე სინათლის დიფრაქციისას რხევის ინტენსივობა
მესერის ფორმულიდან გამომდინარე, მთავარი მაქსიმუმების მდებარეობა (ნულოვანის გარდა) λ ტალღის სიგრძეზეა დამოკიდებული. ამიტომას მესერს შეუძლია გამოსხივების სპექტრად დაშლა, ე.ი. ის სპექტრულ ხელსაწყოს წარმოადგენს. თუ მესერს არამონოქრომატული გამოსხივება ეცემა, მაშინ დიფრაქციის ყოველ რიგში (ანუ m -ის ყოველი მნიშვნელობისთვის) საკვლევის გამოსხივების სპექტრი წარმოიშვება, ამასთან სპექტრის იისფერი ნაწილი ნულოვანი რიგის მაქსიმუმისკენაა განთავსებული. ნახ. 6-ზე თეთრი სინათლისთვის სხვადასხვა რიგის სპექტრებია გამოსახული. ნულოვანი რიგის მაქსიმუმი შეუფერავი რჩება.
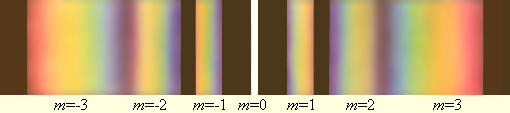
ნახ. 6.
თეთრი სინათლის დაშლა დიფრაქციული მესერის სასუალებით
დიფრაქციული მესერის საშუალებით შესაძლებელია ტალღის სიგრძის ძალიან ზუსტი გაზომვა. თუ მესერი d პერიოდი ცნობილია, მაშინ ტალღის სიგრძის განსაზღვრა m -ური რიგის სპექტრში არჩეული ხაზის მიმართულების შესაბამისი θm კუთხის გაზომვამდე დაიყვანება. პრაქტიკაში ჩვეულებრივ პირველი და მეორე რიგის სპექტრები გამოიყენება.
თუ საკვლევის გამოსხივების სპექტრში ორი სპექტრული ხაზია λ1 და λ2 ტალღის სიგრძეებით, მაშინ მესერს ყოველ სპექტრულ რიგში (გარდაm = 0) შეუძლია ერთი ტალღის მეორისაგან განცალკევება.
დიფრაქციული მესერის ერთ-ერთ უმნიშვნელოვანეს მახასიათებელს მისი გარჩევის უნარი წარმოადგენს, რომელიც მოცემული მესერის საშუალებით λ და λ + Δλ ტალღის სიგრძეების მქონე ორი ახლომდებარე სპექტრული ხაზის გარჩევის შესაძლებლობას ახასიათებს. სპექტრული გარჩევის უნარი R ეწოდება λ ტალღის სიგრძის ფარდიბას Δλ-ს მინიმალურ შესაძლო მნიშვნელობასთან, ანუ

სპექტრული ხელსაწყოების გარჩევის უნარი, და კერძოდ, დიფრაქციული მესერისა, ისევე როგორც ოპტიკური ინსტრუმენტების (ტელესკოპი, მიკრისკოპი) ზღვრული გარჩევა, სინათლის ტალღური ბუნებით განისაზღვრება. ითვლება, რომ ორი ახლომდებარე ხაზის m -ური რიგის სპექტრში განირჩევა, თუ λ + Δλ ტალღის სიგრძისათვის მთავარი მაქსიმუმი λ ტალღის სიგრძის მთავრი მაქსიმუმისაგან მტავარი მაქსიმუმის ნახევარსიგანეზე ნაკლებით, ე.ი. δθ = λ / Nd-ით. ფაქტიურად ეს სპექტრული ხელსაწოებისათვის გამოყენებული რელეის კრიტერიუმია. მესერის ფორმულიდან გამოდის, რომ:
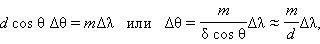
სადაც Δθ – m -ური რიგის სპექტრში ორი ახლომდებარე, ტალღის სირძეებს შორის Δλ სხვაობით, ხაზის მთავარ მაქსიმუმებს შორის კუთხური მანძილია. სიმარტივისათვის იგულისხმება, რომ დიფრაქციის კუთხეები მცირეა (cos θ ≈ 1). Δθ და δθ- ს გატოლებით მესერის გარჩევის ძალის შეფასებას მივიღებთ:

ამგვარად, დიფრაქციული მესერის ზღვრული გარჩევა მხოლოდ სპექტრის რიგზე და მესერის პერიოდების N რიცხვზეა დამოკიდებული.
ვთქვათ მესერის პერიოდია d = 10–3 მმ, მისი სიგრძე L = 10 სმ. მაშინ, N = 105 (ეს კარგი მესერია). მეორე რიგის სპექტრისათვის მესერის გარჩევის უნარი ტოლია R = 2·105. ეს ნიშნავს, რომ ტალღის სიგრძეების მინიმალურად დასაშვები ინტერვალი სპექტრის მწვანე უბანში (λ = 550 ნმ) ტოლია Δλ = λ / R ≈ 2,8·10–3 ნმ. იგივე პირობებში d = 10–2 მმ и L = 2 სმ მესერის ზღვრული გარჩევა იქნებოდა Δλ = 1,4·10–1 ნმ-ს ტოლი.


