რხევებს, რომლებიც გარე, პერიოდული ძალების მოქმედებით მიმდინარეობს, იძულებითი ეწოდება.
ამ შემთხვევაში გარეშე ძალა ასრულებს დადებით მუშაობას და უზრუნველყოფს მერხევ სისტემაში ენერგიის მოდინებას. მიუხედავად ხახუნის ძალების მოქმედებისა, ის რხევას მილევის საშუალებას არ აძლევს.
პერიოდული გარე ძალა შეიძლება სხვადასხვა კანონით იცვლებოდეს დროში. განსაკუთრებულ ინტერესს იწვევს შემთხვევა, როცა გარეშე ძალა, რომელიც \(\omega\) სიხშირით, ჰარმონიული კანონით იცვლება, მოქმედებს მერხევ სისტემაზე, რომელსაც შეუძლია საკუთარი რხევის შესრულება რაღაც \(\omega_{0}\) სიხშირით.
თუ თავისუფალი რხევა ω0 სიხშირით ხდება, რომელიც განისაზღვრება სისტემის პარამეტრებიდან. მაშინ იძულებითი რხევა ყოველთვის გარეშე ძალის \(\omega\) სიხშირეზე მიმდინარეობს.
მერხევ სისტემაზე გარე ძალის მოქმედების დაწყებიდან საჭიროა რაღაც \(\Delta t\) დროის გასვლა იძულებითი რხევის დადგომამდე. ეს დრო რიგის მიხედვით ტოლია მერხევი სისტემის თავისუფალი რხევის მილევის \(\tau\) რდოისა.
საწყის მომენტში მერხევ სისტემაში აღიძვრება ორივე პროცესი – ω სიხშირის იძულებითი რხევა და თავაისუფალი რხევა საკუთარი \(\omega_{0}\) სიხშირით. მაგრამ თავისუფალი რხევა მიილევა გარდუვალი ხახუნის ძალების არსებობის გამო. ამიტომ რაღაც დროის შემდეგ მერხევ სისტემაში რჩება მხოლოდ მაიძულებელი ძალის \(\omega\) სიხშირის სტაციონალური რხევა.
 |
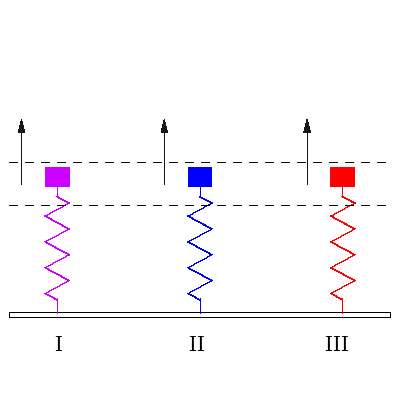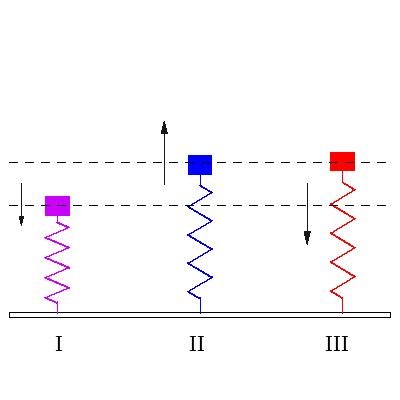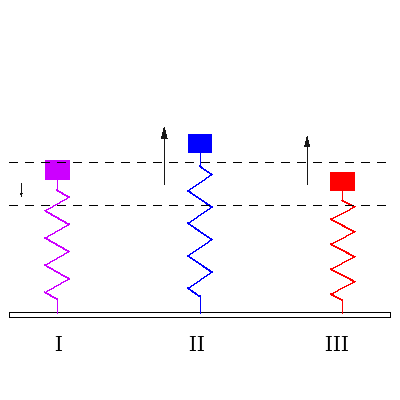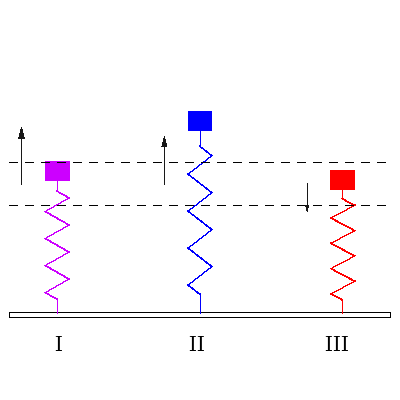I იძულებითი რხევის დასაწყისი, როცა გვაქვს ორივე გარეშე ძალის სიხშირე და ქანქარას სიხშირე ერთად. II. ჩამოყალიბებული რეზონანსი, როცა გარე ძალის სიხშირე ემთხვევა ქანქარას საკუთარ სიხშირეს. III. ჩამოყალიბებული იძულებითი რხევა, როცა ზამბარის საკუთარი სიხშირით რხევა მიილია და ის ირხევა გარეშე ძალის სიხშირით. |
მაგალითისთვის განვიხილოთ ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევა (ნახ. 2.5.1). გარეშე ძალა \(\vec{F}_{gare}\) ზამბარის თავისუფალ ბოლოზეა მოდებული. ის ზამბარის ბოლოს აიძულებს გადაადგილდეს კანონით:
\(y=y_{m}\cos \omega t\).
სადაც ym – რხევის ამპლიტუდაა, ω – წრიული სიხშირე.
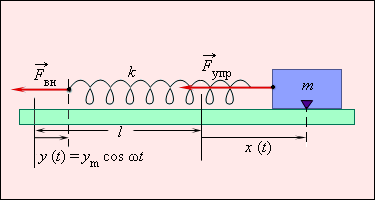
ნახ. 1.
ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევა. ზამბარის თავისუფალი ბოლო გადაადგილდება კანონით \(y=y_{m}\cos \omega t\). \(l\) – დეფორმირებული ზამბარის სიგრძე, \(k\) – ზამბარის სიხისტე.
თუ ზამბარის დეფორმაციის შედეგად მისი მარცხენა ბოლო საწყისი მდებარეობიდან \(y\) მანძილზეა წანაცვლებული, ხოლო მარჯვენა – \(x\)–ზე, მაშინ ზამბარის წაგრძელება Δl ტოლია:
\(\Delta l=x-y=x-y_{m}\cos\omega t\).
\(M\) მასის სხეულისთვის ნიუტონის მეორე კანონი მიიღებს სახეს:
\(ma=-k(x-y)=-kx+ky_{m}\cos \omega t\).
ამ განტოლებაში სხეულზე მომქმედი ძალა ორი შესაკრების სახითაა წარმოდგენილი. მარჯვენა მხარეს პირველი შესაკრები დრეკადი ძალაა, რომელიც სხეულის წონასწორობაში (\(x=0\)) დაბრუნებას ცდილობს. მეორე შესაკრები – სხეულზე გარე პერიოდული ზემოქმედებაა. სწორედ ამ შესაკრებს უწოდებენ მაიძულებელ ძალას.
ამ განტოლებას შეიძლება მივცეთ მკაცრი მათემატიკური სახე, თუ გავიხსენებთ კავშირს სხეულის აჩქარებასა და კოორდინატს შორის: \(a=x''\). მაშინ იძულებითი რხევის განტოლება ჩაიწერება შემდეგი სახით:
\(x''+\omega_{0}^{2}x=A\cos\omega t,\) (**)
სადაც \(\omega_{0}=\sqrt{\frac{k}{m}}\) – მაიძულებელი ძალის ციკლური სიხშირე. ზამბარაზე მიმაგრებული სხეულის იძულებითი რხევის შემთხვევაში (ნახ. 1) \(A\) სიდიდე განისაზღვრება გამოსახულებით:
\(A=\frac{k}{m}y_{m}=\omega_{0}^{2}y_{m}.\)
განტოლება (**) ხახუნის ძალებს არ ითვალისწინებს. თავისუფალი რხევის განტოლებისგან (*) განსხვავებით იძულებითი რხევის განტოლება (**) შეიცავს ორ სიხშირეს – თავისუფალი რხევის სიხშირეს \(\omega_{0}\) და მაიძულებელი რხევის სიხშირეს \(\omega\).
საბოლოოდ ზამბარაზე დამყარებული ტვირთის იძულებითი რხევა გარედან ზემომქმედების სიხშირით მიმდინარეობს შემდეგი კანონით
\(x(t)=x_{m}\cos(\omega t+\theta )\).
იძულებითი რხევის ამპლიტუდა \(x_{m}\) и და ფაზა \(\theta\) დამოკიდებილია \(\omega_{0}\)–ს და \(\omega\)–ს თანაფარდობაზე და გარე ძალის ამპლიტუდაზე <m>m>ym .
ძალიან დაბალი სიხშირეებისთვის, როცა \(\omega<<\omega_{0}\), ზამბარის მარჯვენა ბოლოსთან მიმაგრებული \(m\) მასის სხეულის მოძრაობა მარცხენა ბოლოს მოძრაობას იმეორებს. ამასთან \(x(t)=y(t)\), და ზამბარა პრაქტიკულად დეფორმირებული რჩება. ზამბარის მარცხენა ბოლოზე მოდებული გარეშე ძალა \(\vec{F}_{gare}\) მუშაობას არ ასრულებს, რადგან მისი ძალის მოდული როცა \(\omega<<\omega_{0}\) ნულისაკენ მიისწაფის.
თუ გარე ძალის სიხშირე \(\omega\) თავისუფალ სიხშირეს \(\omega_{0}\)–ს უახლოვდება ხდება იძულებითი რხევის ამპლიტუდის მკვეთრი ზრდა. ამ მოვლევას რეზონანსს უწოდებენ. იძულებითი რხევის ამპლიტუდის \(x_{m}\) მაიძულებელი ძალის სიხშირეზე \(\omega\)დამოკიდებულებას რეზონანსულ მახასიათებელს ან რეზონანსილ მრუდს უწოდებენ (ნახ. 2).
რეზონანსის დროს ტვირთის რხევის ამპლიტუდა \(x_{m}\) ბევრად აღემატება ზამბარის თავისუფალი ბოლოს გარე ზემოქმედებით გამოწვეული რხევის ამპლიტიდა \(y_{m}\)–ს. ხახუნია არ არსებობისას იძულებითი რხევის ამპლიტუდა რეზონანსის შემთხვევაში შეუზღუდავად უნდა იზრდებოდეს. რეალურ პირობებში დამყარებული იძულებითი რხევის ამპლიტუდა განისაზრვრება პირობით: გარე ძალის მუშაობა რხევის პერიოდის განმავლობაში ტოლი უნდა იყოს იგივე დროში ხახუნით გამოწვეული მექანიკური ენერგიის კარგვისა. რეზონანსის დროს,რაც ნაკლებია ხახუნი (ე.ი. რაც მეტია მერხევი სისტემის ვარგისიანობა \(Q\)), მით მეტია იძულებითი რხევის ამპლიტუდა.
არც თუ მაღალი ვარგისიანობის მქონე (< 10) მერხევი სისტემის რეზონანსული ამპლიტუდის მცირე სიხშირეებისკენ ჩანაცვლება ხდება. ეს კარგად ჩანს ნახ. 2–ზე.
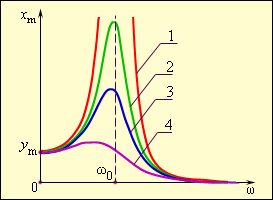
ნახ. 2.
რეზონანსული მრუდები მილევის სხვადასხვა დონისთვის: 1 - რხევითი სისტემა ხახუნის გარეშე: რეზონანსის დროს იძულებითი რხევის ამპლიტუდა \(x_{m}\) იზრდება: 2,3,4, - სხვადასხვა ვარგისიანობის მქონე რხევითი სისტემის რეალური რეზონანსული მრუდები: \(Q_{2}>Q_{3}>Q_{4}\). დაბალ სიხშირეებზე (\(\omega << \omega_{0}\)) \(x_{m}\approx y_{m}\). მაღალ სიხშირეებზე (\(\omega >>\omega_{0}\)) \(x_{m}\rightarrow 0.\)
იძულებითი რხევები მიულევადი რხევებია. ხახუნზე ენერგიის გარდაუვალი კარგვა კომპენსირდება გარე პერიოდული ძალის წყაროს მხრიდან. არსებობენ სისტემები, რომლებშიც რხევის მიულევადობა მიიღწევა არა გარე პერიოდული ზემოქმედებით, არამედ ასეთი სისტემების შესაძლებლობით თვითონ არეგულიროს ენერგიის მოწოდება მუდმივი წყაროდან. ასეთ სისტემებს თვითმერხევს და ასეთ სისტემებში მიულევადი რხევის პროცესს ავტორხევითს უწოდებენ. ავტომერხევ სისტემაში შეიძლება გამოვყოთ სამი მახასიათებელი ელემენტი –მერხევი სისიტემა, ენერგიის წყარო და უკუკავშირის მოწყობილობა სისტამასა და ენერგიის წყაროს შორის. მერხევ სისტემად შეიძლება გამოყენებულ იქნეს ნებისმიერი მექანიკური სისტემა, რომელსაც შეუძლია საკუთარი მილევადი რხევის შესრულება (მაგ. კედლის საათის ქანქარა).
ენერგიის წყაროდ შეიძლენა გამოდგეს ზამბარის დეფორმაციის ენერგია ან მიზიდულობის ველში ტვირთის პოტენციური ენერგია. უკუკავშირის მოწყობილობა წარმოადგენს რაღაც მექანიზმს, რომლითაც თვითმერხევი სისტემა არეგულირებს წყაროდან ენერგიის მიწოდებას. ნახ. 3–ზე თვითმერხევი სისტემის სხვდასხვა ელემენტების ურთიერთქმედების სქემაა გამოსახული.
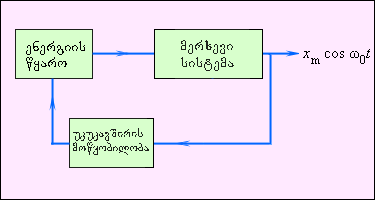
ნახ. 3.
ავტომერხევი სისტემის ფუნქციური სქემა.
მექანიკური თვითმერხევი სისტემის მაგალითად გამოდგემა საათიერი მექანიზმი ანკერიანი (ღუზიანი) სვლით.
ირიბი კბილანების მქონე სავალი ბორბალი მყარადაა დამაგრებული კბილანებიან დოლურასთან, რომელზეც გადადებულია ჯაჭვი საწონით (ტვირთით). ქანქარას ზედა ნაწილზე მიმაგრებულია ანკერი, ორი მაგარი მეტალური ფირფიტით, რომლებიც მოხრილია რკალის ფორმით, რომლის შესაბამისი წრეწირის ცენტრი ქანქარის ღერძის ცენტრს ემთხვევა. ხელის საათებში საწონი ზამზარითაა შეცვლილი.ბალანსატორი ასრულებს ბრუნვით რხევებს თავისი ღერძის გარშემო. საათებში მერხევ სისტემას ქანქარა ან ბალანსატორი წარმოადგენს. ენერგიის წყარო ზევით აწეული საწონი ან დაქოქილი ზამბარაა. მოწყობილობას, რომლის საშუალებითაც ხორციელდება უკუკავშირი, წარმოადგენს ანკერი, რომელის სავალ ნაწილს საშუალებას აძლევს ერთი კბილანით შემობრუნდეს ერთი ნახევარპერიოდის განმავლობაში. უკუკავშირი ხორციელდება ანკერის სავალ ნაწილთან ურთიერთქმედებით. ქანქარის ყოველი რხევისას სავალი ბირბლის კბილანა უბიძგებს ანკერის ჩანგალს ქანქარის მოძრაობის მიმართულებით. ამგვარად, საწონის (ან ჩახვეული ზამბარის) პოტენციური ენერგია თანდათანობით, ცალკეული პორციების სახით ქანქარას გადაეცემა.
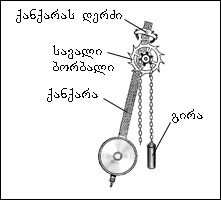
ნახ. 2.5.4.
ქანქარიანი საათის მექანიზმი.
მექანიკური თვითმერხევი სისტემები ფართოდაა გავრცელებული ყოფაცხობრევასა და ტექნიკაში. ავტორხევებს ასრულებენ ორთქლის მანქანები, შიგაწვის ძრავები, ელექტრული ზარი, ხემიანი სიმიანი მუსიკალური ინსტრუმენტები, ჰაერის სვეტები სასულე ინსტრუმენტებში, ხმის იოგები ლაპარაკის ან სიმღერის დროს და ა.შ.