{loadnavigation}
თავისუფალი მექანიკური რხევების დროს კინეტიკური და პოტენციური ენერგიები პერიოდელად იცვლებიან. წონასწორობის მდებარეობიდან სხეულის მაქსიმალური გადახრისას მისი სიჩქარე, და ე.ი. კინეტიკური ენერგიაც ნულის ტოლი ხდება. ამ მდებარეობაში პოტენციური ენერგია მაქსიმალურ მნიშვნელობას აღწევს. ჰორიზონტულად მიმართულ ზამბარაზე მიმაგრებული ტვირთისთვის პოტენციური ენერგია – ზამბარის დრეკადი დეფორმაციის ენერგიაა. მათემატიკური ქანქარასთვის – დედამიწის მიზიდულობის ველი.
როცა სხეული მოძრაობისას წონასწორობის მდებარეობას გადის, მისი სიჩქარე მაქსიმალურია. ამ დროს მას მაქსიმალური კინეტიკური და მინიმალური პოტენციური ენერგია აქვს. კინეტიკური ენერგიის გადიდება პოტენციური ენერგიის ხარჯზე ხდება. შემდგომი მოძრაობისას პოცენციური ენერგია იწყებს მატებას კინეტიკური ენერგიის შემცირების ხარჯზე და ა.შ.
ამგვარად, ჰარმონიული რხევებისას ხდება კინეტიკური ენერგიის პერიოდელი გარდაქმნა პოტენციურ ენერგიად და პირიქით.
თუ მერხევ სისტემაში ხახუნი არ არის, თავისუფალი რხევისას სრული ენერგია უცვლელი რჩება.
ზამბარაზე მიმაგრებული ტვირთისათვის:
\(E=E_{k}+E_{p}=\frac{mv^{2}}{2}+\frac{kx^{2}}{2},\; \omega_{0}^{2}=\frac{k}{m},\)
\((E_{p})_{max}=\frac{kx_{m}^{2}}{2},\: (E_{k})_{max}=\frac{mv_{m}^{2}}{2}=\frac{m\omega_{0}^{2}x_{m}^{2}}{2}=(E_{p})_{max}.\)
მათემატიკური ქანქარის მცირე რხევებისთვის:
\(E=E_{k}+E_{p}=\frac{mv^{2}}{2}+mgh=\frac{mv^{2}}{2}+\frac{mgx^{2}}{2l},\: \omega_{0}^{2}=\frac{g}{l},\)
\((E_{p})_{max}=mgh_{m}=\frac{mgx_{m}^{2}}{2l},\: (E_{k})_{max}=\frac{mv_{m}^{2}}{2}=\frac{m\omega_{0}^{2}x_{m}^{2}}{2}=(E_{p})_{max}.\)
აქ \(h_{m}\) – დედამიწის მიზიდულობის ველში ქამქარას ასვლის მაქსიმალური სიმაღლეა, \( x_{m}\) და \(v_{m}=\omega_{0}x_{m}\) – წონასწორობის მდგომარეობიდან ქანქარას მაქსიმალური გადახრა და მისი სიჩქარე.
თავისუფალი მექანიკური რხევისას ხახუნის არ ქონის შემთხვევაში, ენერგიის გარდაქმნა შეიძლება გრაფიკულად გამოისახოს. მაგალითისთვის განვიხილოს \( m\) მასის ტვირთის რხევა \(k\) სიხისტის ზამბარაზე. ვთქვათ წონასწორობის მდგომარეობიდან ტვირთის გადახრა \( x(t)\) და მისი სიჩქარე \(v(t)\) დროში შემდეგი კანონით იცვლება:
\(x(t)=x_{m}\cos(\omega_{0}t),\) სადაც \(\omega_{0}^{2}=\frac{k}{m},\)
\(v(t)=-\omega x_{m}\sin{(\omega_{0}t)}.\)
აქედან გამომდინარე,
\(E_{p}(t)=\frac{1}{2}kx^{2}=\frac{1}{2}kx_{m}^{2}\cos^{2}\omega_{0}t=\frac{1}{4}kx_{m}^{2}(1+\cos 2\omega_{0}t),\)
\(E_{k}(t)=\frac{1}{2}mv^{2}=\frac{1}{2}k\omega_{0}^{2}x_{m}^{2}\sin^{2}\omega_{0}t=\frac{1}{4}kx_{m}^{2}(1-\cos 2\omega_{0}t).\)
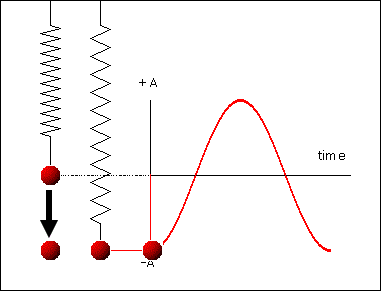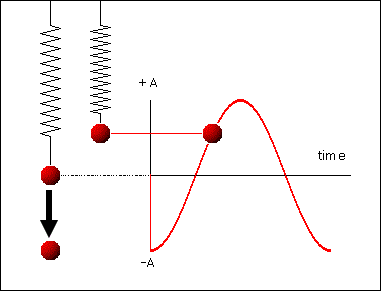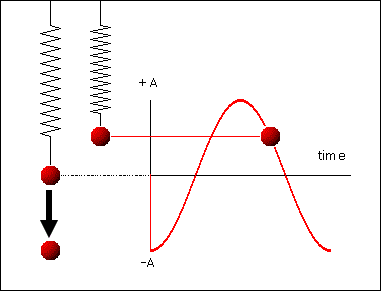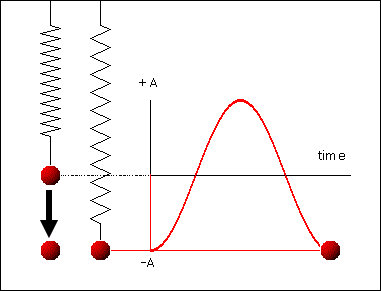
ნახ. 1–ზე \(E_{p}(t)\) და \(E_{k}(t)\) ფუნქციების გრაფიკებია გამოსახული. რხევის პერიოდის განმავლობაში \(T=\frac{2\pi}{\omega_{0}}\) კინეტიკური და პოტენციური ენერგიები ორჯერ აღწევეს მაქსიმალურ მნიშვნელობას. ჯამი \(E_{p}(t)+E_{k}(t)=E=const\) უცვლელი რჩება.


ნახ. 1.
ენერგიის გარდაქმნა თავისუფალი რხევის დროს
რეალურ პირობებში ნებისმიერი მერხევი სისტემა ხახუნის (წინაღმდეგობის) ძალების მოქმედებას განიცდის. ამ დროს მექანიკური ენერგიის ნაწილი ატომებისა და მოლეკულების სითბური მოძრაობის შინაგან ენერგიად გარდაიქმნება და რხევა მილევადი ხდება (ნახ. 2).

ნახ. 2.
მილევადი რხევა
რხევის მილევის სიჩქარე ხახუნის ძალების სიდიდეზეა დამოკიდებული. დროის ინტერვალს \(\tau\), რომლის განმავლობაშიც რხევის ამპლიტუდა \(e\approx 2,7\)–ჯერ მცირდება, დროით მილევას უწოდებენ.
თავისუფალი რხევის სიხშირე მისი მილევის სიჩქარეზეა დამოკიდებული. მაგრამ, საკუთარი სიხშირის ცვლილება მხოლოდ ხახუნის ძალების საკმარისად დიდი მნიშვნელობებისთვის ხდება შესამჩნევი, როცა საკუთარი სიხშირე სწრაფად მიილევა.
მერხევი სისტემის, რომელიც თავისუფალ მილევად მოძრაობას ასრულებს, მნიშვნელოვან მახასიათებელს ვარგისიანობა \(Q\) წარმოადგენს. ეს პარამეტრი განისაზღვრება, როგორც მილევის \(\tau\) პერიოდის განმავლობაში სისტემის მიერ შესრულებული სრულ რხევათა \(N\) რიცხვის ნამრავლი \(\pi\)–ზე:
\(Q=\pi N=\pi\frac{\tau}{T}.\)
რაც უფრო ნელა ხდება რხევის მილევა, მით მეტია მერხევი სისტემის ვარგისიანობა \(Q\). ნახ. 2–ზე მოცემული მერხევი სისტემის ვარგისიანობა 15–ის ტოლია.
მექანიკური მერხევი სისტემის ვარგისიანობა შეიძლება ძალიან დიდი იყოს, რამდენიმე ასეულის და ათასეულის რიგისაც.
ვარგისიანობის ცნებას ღრმა ენერგეტიკული არსი აქვს. მერხევი სისტემის ვარგისიანობა \(Q\) შეიძლება განისაზღვროს ენერგეტიკული ფარდობით:
\(Q=2\pi\) მერხევი სისტემის ენერგიის მარაგი/ენერგიის დანაკარგი რხევის 1 პერიოდის განმავლობაში.
ამგვარად, ვარგისიანობა ახასიათებს მერხევი სისტემის, ხახუნის არსებობით გამოწვეულ, ენერგიის ფარდობით დანაკლისს ერთი სრული რხევის დროის ტოლ ინტერვალში.
{loadnavigation}
მათიმათიკური ქანქარას დიდ ზომის სხეულს უწოდებენ, რომელიც წვრილ უჭიმვად ძაფზეა დაკიდებული და ამ ძაფის მასის უგულვებელყოფაა შესაძლებელი, მისი მასის სიმცირის გამო სხეულის მასასთან შედარებით. წონასწორობის მდგომარეობაში, როცა ქანქარა უძრავად ჰკიდია, სიმძიმის ძალა \(m\vec{g}\) დრეკადობის \(\vec{F}_{drek}\) ძალითაა გაწონასწორებული. ქანქარას წონასწორობის მდგომარეობიდან φ კუთხით გადახრის შემთხვევაში წარმოიქმნება სიმძიმის ძალის მდგენელი \(F_{\tau}=-mg\sin \phi\) , რომელიც ქანქარას მოძრაობის ტრაექტორიის მხების გასწცრივაა მიმართული (ნახ. 1). ამ ფორმულაში „–„ მიუთითებს, რომ ეს მდგენელი მიმართულია ქანქარას გადახრის საწინააღმდეგოდ.


ნახ. 1.
მათემატიკური ქანქარა. \(\phi\) – ქანქარას კუთხური გადახრა წონასწორობის მდგომარეობისა, \(x=l\phi\) – ქანქარას გადახრა რკალზე.
თუ \(x\)–ით აღვნიშნავთ ქანქარას გადახრას წონასწორული მდგომარეობის l რადიუსის მქონე წრის რკალზე, მაშინ მისი კუთხური გადაადგილება ტოლია \(\phi=\frac{x}{l}\). ნიუტონის მეორე კანონი, რომელიც ჩაწერილია მხების მიმართულებაზე აჩქარებისა და ძალის გეგმილებით, იძლევა:
\(ma_{\tau}=F_{\tau}=-mg\sin \frac{x}{l}.\)
ეს თანაფარდობა უჩვენებს, რომ მათემატიკური ქანქარა რთულ არაწრფივ სისტემას წარმოადგენს, რადგან ძლა, რომელიც ქანქარას წონასწორობაში დაბრუნებას ცდილობს პროპორციულია არა \(x\) გადაადგილებისა, არამედ \(\sin \frac{x}{l}\)–სა.
მხოლოდ მცირე რხევების შემთხვევაში, როცა \(\sin \frac{x}{l}\) დაახლოებით შეიძლება შეიცვალოს \(\frac{x}{l}\) მათამატიკური ქანქარა შეიძლება ჩაითვალოს ჰარმონიულ ოსცილატორად, ე.ი. სისტემად, რომელსაც შეუძლია ჰარმონიული რხევის შესრულება. პრაქტიკულად ასეთი მიახლოება სამართლიანია მხოლოდ 15–20° ტოლი კუთხეებისათვის; ამასთან, სიდიდე \(\sin \frac{x}{l}\) განსხვავდება \(\frac{x}{l}\) –სგან არაუმეტეს 2 %–ით. ქანქარას რხევა დიდი ამპლიტუდების შემთხვევაში ჰარმონიული არ არის.
მცირე რხევების შემთხვევაში მათემატიკური ქანქარასთვის ნიუტონის მერე კანონი ჩაიწერება შემდეგი სახით:
\(ma_{\tau}=-m\frac{g}{l}x.\)
ამგვარად, ქანქარას ტანგენციური აჩქარება \(a_{\tau}\) პროპორციულია საწინააღმდეგო ნიშნით აღებული მისის \(x\) გადაადგილების. ეს სწორედ ის პირობაა, როცა სისტემა სისტემა ჰარმონიულ ოსცილატორს წარმოადგენს. ზოგადი წესის მიხედვით ყველა სისტემისათვის, რომლებსაც შეუძლიათ თავისუფალი ჰარმონიული რხევის შესრულება, აჩქარებასა და წონასწორობის მდგომარეობიდან გადაადგილებას შორის პროპორციულობის კოეფიციენტის მოდული წრიული სიხშირის კვადრატის ტოლია:
\(\omega_{0}^{2}=\frac{g}{l};\; \omega_{0}=\sqrt{\frac{g}{l}}.\)
ეს ფორმულა გამოსახავს მათემატიკური ქანქარას მცირე რხევის საკუთარ სიხშირეს.
აქედან გამომდინარე,
\(T=\frac{2\pi}{\omega_{0}}=2\pi\sqrt{\frac{l}{g}}.\)
ჰორიზონტულ ბრუნვის ღერძზე დამაგრებულ ნებისმიერი სხეულს, მიზიდულობის ველში, შეუძლია შეასრულის თავისუფალი რხევა და, ე.ი. ქანქარას წარმოადგენს. ასეთ ქანქარას ფიზიკურს უწოდებენ (ნახ.2). ის მათემატიკურისაგან მხოლოდ მასის განაწილებით გასხვავდება. მყარი წონასწორობის მდგომარეობაში ფიზიკური ქანქარას მასათა ცემტრი \(C\) მდებარეობს \(O\) ბრუნვის ღერძზე გამავალ მართობზე. ქანქარას \(\phi\) კუთხით გადახრის შემთხვევაში წარმოიქმნება ძალის მომენტი, რომელიც ქანქარას წონასწორობის მდგომარეობაში დაბრუნებას ცდილობს:
\(M=-(mg\sin \phi)d\).
სადაც \(d\) – ბრუნვის ღერძსა და მასათა ცენტრს \(C\) შორის მანძილია.

ნახ. 2.
ფიზიკური ქანქარა
ამ ფორმულაში „–“ , ჩვეულებრივ ნიშნავს, რომ ძალის მომენტი ქანქარას მობრუნებას ცდილობს წონასწორობიდან მისი გადახრის საწიმააღმდეგოდ. მათემატიკური ქანქარას შემთხვევის მსგავსად, დამაბრუნებელი მომენტი \(M\) , \(\sin \phi\)–ს პროპორციულია. ეს ნიშნავს, რომ მხოლოდ მცირე \(\phi\) კუთხის შემთხვევაში, როცა \(\sin \phi\approx \phi\), ფიზიკურ ქანქარას შეუძლია თავისუფალი ჰარმონიული რხევის შესრულება. მცირე რხევების შემთხვევაში
\(M=-mgd\phi\).
ფიზიკურ ქანქარასთვის ნიუტონის მეორე კანონს აქვს სახე
\(I\varepsilon=M=-mgd\phi\).
სადაც \(\varepsilon\) – ქანქარას კუთხური აჩქარებაა, \(I\) – ბრუნვის \(O\) ღერძის მიმართ ქანქარას ინერციის მომენტი. აჩქარებასა და წონასწორობის მდგომარეობიდან გადახრას შორის პროპორციულობის კოეფიციენტის მოდული წრიული სიხშირის კვადრატის ტოლია:
\(\omega_{0}^{2}=\frac{mgd}{I}\) ან \(\omega_{0}=\sqrt{\frac{mgd}{I}}.\)
აქ \(\omega_{0}\) – ფიზიკური ქანქარას მცირე რხევის საკუთარი სიხშირეა.
აქედან გამომდინარე,
\(T=\frac{2\pi}{\omega_{0}}=2\pi\sqrt{\frac{I}{mgd}}.\)
\(\omega_{0}\) -სთვის და \(T\)-სთვის უფრო მკაცრ ფორმულებს მივიღებთ, თუ მხედველობაში მივიღებთ კუთხურ აჩქარებასა და კუთხურ გადახრას შორის მათემატიკურ კავშირს: კუთხურ აჩქარება \(\varepsilon\) კუთხურ \(\phi\) გადახრის დროითი მეორე წარმოებულია:
\(\varepsilon (t)={\phi}''(t).\)
ამიტომ ნიუტონის მეორე კანონის გამომსახველ განტოლებას ფიზიკური ქანქარასთვის ექნება სახე:
\({\phi}''+\frac{mgd}{I}\phi=0.\)
ეს თავისუფალი ჰარმონიული რხევის განტოლებაა. ამ განტოლებაში \(\frac{mgd}{I}\) კოეფიციენტს ფიზიკური ქანქარას თავისუფალი ჰარმონიული რხევის წრიული სიხშირის არსი აქვს.
ბრუნვის ღერძის პარალელური გადატანის თეორემის (შტეინერის თეორემა) მიხედვით ინერციის მომენტი \(I\) შეიძლება გამოისახოს ქანქარას მასათა \(C\) ცენტრზე გამავალ და ბრუნვის ღერძის პარალელური ღერძის ინერციის მომენტის \(I_{C}\) –ს საშუალებით:
\(I=I_{C}+md^{2}\).
საბოლოოდ, ფიზიკური ქანქარას თავისუფალი ჰარმონიული რხევის წრიული \(\omega_{0}\) სიხშირისათვის მივიღებთ გამოსახულებას:
\(\omega_{0}=\sqrt{\frac{mgd}{I_{C}+md^{2}}}.\)
{loadnavigation}
თავისუფალი რხევა აღიძვრება, სისტემის წონასწორობის მდგომარეობიდან გამოყვანის შემდეგ, სისტემის შინაგანი ძალების მოქმედებით.
თავისუფალი რხევა რომ ჰარმონიული კანონით მიმდინარეობდეს, საჭიროა, ძალა, რომელიც სხეულის წონასწორულ მდგომარეობაში დაბრუნებას ცდილობს სხეულის წონასწორობიდან წანაცვლების პროპორციული იყოს და საწიმააღმდეგოდ იყოს მიმართული.
\(F(t)=ma(t)=-m\omega^{2}x(t)\).
ამ გამოსახულებაში \(\omega\) – ჰარმონიული რხევის წრიული სიხშირეა. დრეკადობის ძალა ჰუკის კანონის გამოყენების ფარგლებში ტოლია:
\(F_{drek}=-kx\).
სხვა ნებისმიერი ფიზიკური ბუნების მქონე ძალას, რომელიც იგივე პირობას აკმაყოფილებს კვაზიდრეკადს უწოდებენ.
ამგვარად, \(k\) სიხისტის მქონე ზამბარა, რომლის ერთი ბოლო უძრავადაა დამაგრებული, მეორეზე კი \(m\) მასის ტვირთია მიმაგრებული, ქმნის სისტემას, რომელსაც ხახუნის არ არსებობის შემთხვევაში შეუძლია ჰარმონიული რხევის შესრულება. ზამბარაზე მიმაგრებულ ტვირთს წრფივ ჰარმონიულ ოსცილატორს უწოდებენ.

ნახ. 1.
ზამბარაზე მიმაგრებული ტვირთის რხევა. ხახუნი არ გვაქვს.
ტვირთის თავისუფალი რხევის წრიული სიხშირე ω0 ნიუტონის მეორე კანონის საშუალებით გამოითვლება:
\(ma=-kx=m\omega_{0}^{2}x,\)
საიდანაც
\(\omega_{0}=\sqrt{\frac{k}{m}}.\)
ω0 სიხშირეს მერხევი სისტემის თავისუფალ სიხშირეს უწოდებენ.
ტვირთის ჰარმონიული რხევის პერიოდი \(T\) ტოლია
\(T=\frac{2\pi}{\omega_{0}}=2\pi \sqrt{\frac{m}{k}}.\)

როცა სისტემა ზამბარა–ტვირთი ჰორიზონტულადაა განლაგებული ტვირთზე მოდებული სიმძიმის ძალა საყრდენის რეაქციის ძალითაა გაწონასწორებული.


თუ ტვირთი ზამბარაზეა ჩამოკიდებული, მაშინ სიმძიმის ძალის მიმართულება ტვირთის მოძრაობის მიმართულებას ემთხვევა. წონასწორობის მდგომარეობაში ზამბარა \(x_{0}\) სიდიდითაა გაჭიმული, რომელიც ტოლია
\(x_{0}=\frac{mg}{k},\)
და რხევა წონასწორობის ამ ახალი მდებარეობის მახლობლად სრულდება. ω0 თავისუფალი სიხშირისა და რხევის T პერიოდის ზევით მოყვანილი გამოსახულებები ამ შემთხვევაშიც სამართლიანია.
მერხევი სისტემის ქცევის მკაცრი აღწერა შეიძლება მოვივანოტ, თუ გავითვალისწინებთ მათემატიკურ კავშირს სხეულის აჩქარებასა და მის კოორდინატას შორის: აჩქარება სხეულის \(x\) კოორდინატის \(t\) დროით მეორე წარმოებულის ტოლია:
\(a(t)={x}''(t).\)
ამიტომაც. ზამბარაზე ჩამოკიდებული ტვირთისთვის ნიუტონის მეორე კანონი ასე შეიძლება ჩაიწეროს:
\(ma=m{x}''=-kx,\)
ან
\({x}''+\omega_{0}^{2}x=0,\) (*)
სადაც \(\omega_{0}^{2}=\frac{k}{m}.\)
ყველა ფიზიკურ სისტემას (არა მხოლოდ მექანიკურ), რომელიც (*) განტოლებით აღიწერება, თავისუფალი ჰარმონიული რხევის შესრულება შეუძლია, რადგანაც ამ განტოლების ამონახსნი \(x=x_{m}\cos (\omega t+\phi_{0})\) სახის ჰარმონიულ ფუნქციას წარმოადგენს.
(*) განტოლებას თავისუფალი რხევის განტოლებას უწოდებენ. ყურადღება უნდა მიექცეს იმას, რომ მერხევი სისტემის ფიზიკური თვისებები განსაზღვრავენ რხევის საკუთარ სიხშირს \(\omega_{0}\) ან \(T\) პერიოდს. რხევითი პროცესის ისეთი პარამეტრები, როგორიცაა \(x_{m}\) ამპლიტუდა და საწყისი ფაზა φ0 განისაზღვრება იქიდან გამომდინარე თუ დროის საწყის მომენტში სისტემა რა ხერხით იქნა გამოყვანილი წონასწორობის მდგომარეობიდან.
თუ, მაგალითად, ტვირთი წონასწორობის მდგომარეობიდან Δl მანძილზე იქნა გადანაცვლებული და \(t=0\) საწყის მომენტში საწყისი სიჩქარის გარეშე გათავისუფლებული, მაშინ \(x_{m}=\Delta l\), \(\phi_{0}=0\).
თუ ტვირთს წონასწორობის მდგომარეობაში უეცარი ბიძგით მიანიჭეს საწყისი სიჩქარე \(\pm v_{0}\), მაშინ \(x_{m}=\sqrt{\frac{m}{k}}v_{0}\), \(\phi_{0}=\pm \frac{\pi}{2}.\)
ამგვარად. თავისუფალი რხევის \(x_{m}\) ამპლიტუდა და საწყისი ფაზა \(\phi_{0}\) საწყისი პირობებიდან გამომდინარე განისაწღვრება.
არსებობს მექანიკური რხევითი სისტემების დიდ ნაირსახეობა, რომლებშიც დრეკადი დეფორმაციის ძალებია გამოყენებული. ნახ. 2–ზე ნაჩვენებია წრფივი ჰარმონიული ოსცილატორის კუთხური ანალოგი, რომელიც ბრუნვით რხევებს ასრულებს. ჰორიზონტულად განლაგებული დისკი მასათა ცენტრზე მიმაგრებულ უჭიმვად ძაფზე ჰკიდია. \(\theta\) კუთხით დისკის მობრუნებისას აღიძვრება გრეხვის დეფორმაციის ძალის მომენტი \(M_{drek}\):
\(M_{drek}=-\chi \theta\).
ეს თანაფარდობა გრეხვის დეფორმაციისთვის ჰუკის კანონს გამოსახავს. სიდიდე \(\chi\) ზამბარის \(k\) სიხისტის ანალოგიურია. ნიუტონის მეორე კანონი დისკის ბრუნვითი მოძრაობისთვის ჩაიწერება შემდეგი სახით(პარაგრაფი 1.23)
\(I\varepsilon=M_{drek}=-\chi \theta\) ან \(I{\theta} ''=-\chi \theta ,\)
სადაც \(I=I_{C}\) – დისკის ინერციის მომენტია მასათა ცენტრზე გამავალი ღერძის მიმართ, \(\varepsilon\) – კუთხური აჩქარება.
ზამბარაზე ტვირთის ანალოგიურად შეიძლება მივიღოთ:
\(\omega_{0}=\sqrt{\frac{x}{I}},\: \: T=2\pi\sqrt{\frac{I}{x}}.\)
მბრუნავი ქანქარა ფართოდ გამოიყენება მექანიკურ საათებში. მასში დრეკადი ძალების მომენტი სპირალური ზამბარის საშუალებით მიიღწევა.

ნახ. 2.
მბრუნავი ქანქარა
{loadnavigation}
გადატანითი და ბრუნვითი მოძრაობების გვერდით მექანიკაში მნიშვნელოვანი ადგილი რხევით მოძრაობას უკავია. მექანიკურ რხევებს უწოდებენ სხეულის რხევებს, რომლებიც ზუსტად (ან დაახლოებით) მეორდება ერთნაირი დროის ინტერვალებში. მოძრავი სხეულის მოძრაობას კანონი დროის რაღაც პერიოდული \(x=f(t)\) ფუნქციაა. ამ ფუნქციის გრაფიკული გამოსახულება რხევითი პროცესის დროში მიმდინარეობაზე ნათელ წარმოდგენას იძლევა.
რხევითი სისტემების უბრალო მაგალითს ზამბარაზე დაკიდებული ტვირთი ან მათემატიკური ქანქარა წარმოადგენს (ნახ. 1).

ნახ.1
მექანიკური რხევითი სისტემა
მექანიკური რხევები, ისევე როგორც ნებისმიერი ბუნების რხევითი პროცესები, შიძლება იყოს თავისუფალი და იძულებითი. თავისუფალი რხევა, მას შემდეგ რაც სისტემა გამოყვანილ იქნა წონასწორობის მდგომარეობიდან, სრულდება სისტემის შიგა ძალების მოქმედებით. ზამბარაზე დაკიდებული ტვირთის რხევა ან მათემატიკური ქანქარას რხევა თავისუფალ რხევას წარმოადგენს. რხევას, რომელიც გარე, პერიოდულად ცვლადი ძალიების მოქმედებით ხდება, იძულებითი ეწოდება
რხევითი პროცესის უმარტივეს სახეს ჰარმონიული რხევები წარმოადგენენ, რომლებიც შემდეგი განტოლებით აღიწერება:
\(x=x_{m}\cos (\omega t+\phi _{0})\).
აქ \(x\) – წონასწორობის მდგომარეობიდან გადახრაა, \(x_{m}\) – რხევის ამპლიტუდაა, ე.ი. წონასწორობიდან მაქსიმალური გადახრა, \(\omega\) – რხევის ციკლური ან წრიული სიხშირე, \(t\) – დრო. კოსინუსის ქვეშ მყოფ სიდიდეს \(\phi=\omega t+\phi _{0}\) ჰარმონიული პროცესისფაზას უწოდებენ. როცა \(t=0\), \(\phi=\phi_{0}\), ამიტომ \(\phi_{0}\) საწყის ფაზას უწოდებენ. დროის მინიმალირი ინტერვალი, რომლის შემდეგაც სხეულის მოძრაობა მეორდება რხევის პერიოდს \(T\) უწოდებენ. რხევის პერიოდის შებრუნებულ ფიზიკურ სიდიდეს რხევის სიხშირეს უწოდებენ:
\(f=\frac{1}{T}.\)
რხევის \(f\) სიხშირე აჩვენებს, რამდები რხევა შესრულდა 1 წამში. სიხშირის ერთეილია – ჰერცი. რხევის \(f\) სიხშირე დაკავშირებულია ციკლურ სიხშირესთან და რხევის პერიოდთან შემდეგი თანაფარდობით:
\(\omega=2\pi f=\frac{2\pi}{T}.\)
ნახ. 2–ზე გამოსახულია ჰარმონიული რხევის დროს, სხეულის მდებარეობები დროის ტოლ მონაკვეთებში. ასეთი სურათის მიღება შესაძლებელია ექსპერიმენტულად მერხევი სხეულის სინათლით მოკლე პერიოდული პორციებით განათებისას (სტრობოსკოპული განათება). ისრები სხეულის სიჩქარის ვექტორებს გამოსახავს დროის სხვადასხვა მომენტში.

ნახ. 2.
ჰარმონიული რხევის სტრობოსკოპული გამოსახულება. საწყისი ფაზა \(\phi_{0}=0\). სხეულის თანმიმდევრულ მდებარეობებს შორის დროის ინტერვალი \(\tau =\frac{T}{12}.\)
ნახ. 3–ზე ნაჩვენებია ცვლილებები, რომლებიც ხდება ჰარმონიული პროცესის გრაფიკზე, თუ იცვლება რხევის ამპლიტუდა \(x_{m}\), პერიოდი \(T\) (ან სიხშირე \(f\) ), ან საწყისი ფაზა \(\phi_0\).
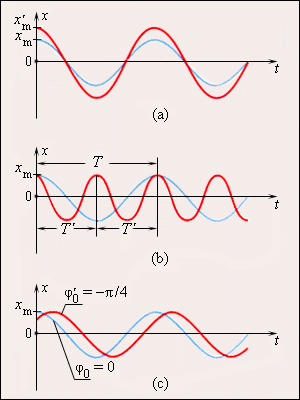
ნახ. 3.
ყველა შემთხვევაში ლურჯი მრუდისთვის \(\phi_{0}=0\): \(a\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ დიდი ამპლიტუდით (\(x_{m}^{'}>x_{m}\)); \(b\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ პერიოდის მნიშვნელობით (\(T^{'}=\frac{T}{2}\)); \(c\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ საწყისი ფაზის მნიშვნელობით (\(\phi_0^{'}=-\frac{\pi}{2}\) რად).
წრფის გასწვრის სხეულის (\(OX\) ღერძი) რხევითი მოძრაობის დროს სიჩქარის ვექტორი ყოველთვის მიმართულია ამ წრფის გასწვრივ.სხეულის სიჩქარე \(v=v_{x}\) განისაზღვრება გამოსახულებით
\(v=\frac{\Delta x}{\Delta t};\: \: (\Delta t\rightarrow 0).\)
როცა \(\Delta t\rightarrow 0\) , \(\frac{\Delta x}{\Delta t}\) ფარდობის ზღვრის პოვნის მათემატიკურ პროცედურას \(x(t)\) ფუნქციისათვის \(t\) დროით წარმოებულის გამოთვლას უწოდებენ და აღნიშნავენ \(\frac{dx(t)}{dt}\) –ით ან \({x}'(t)\) –ით. მოძრაობის ჰარმონიული კანონისათვის \(x=x_{m}\cos (\omega t+\phi_{0})\) წარმოებულის გამოთვლას შემდეგ შედეგებამდე მივყავართ:
\(v={x}'(t)=-\omega x_{m}\sin (\omega t+\phi_{0})=\omega x_{m}\cos \left ( \omega t+\phi_{0}+\frac{\pi}{2} \right ).\)
კოსინუსის არგუმენტში \(+\frac{\pi}{2}\) შესაკრების გამოჩენა საწყისი ფაზის ცვლილებას აღნიშნავს. სიჩქარის მოდულით მაქსიმალური მნიშვნელობები \(v=\omega x_{m}\) დროის იმ მომენტებში მიიღწევა, როცა სხეული წონასწორობის მდებარეობებს გადის (\(x=0\)). ანალოგიურად განისაზღვრება ჰარმონიული რხევისას სხეულის აჩქარებაც \(a=a_{x}\):
\(a=\frac{\Delta v}{\Delta t};\: \: (\Delta t\rightarrow 0),\)
აქდან გამომდინარე, აჩქარება \(a\) ტოლია \(v(t)\) ფუნქციის წარმოებულისა \(t\) დროით, ან \(x(t)\) ფუნქციის მეორე წარმოებულის. გამოთვლების შედეგად ვღებულობთ:
\(a={v}'(t)={x}''(t)=-\omega^{2}x_{m}\cos (\omega t+\phi_{0})=-\omega^{2}x(t).\)
ამ გამოსახულებაში ნიშანი მინუსი აღნიშნავს, რომ \(a(t)\) აჩქარებას ყოველთვის \(x(t)\) გადაადგილების საწინააღმდეგო ნიშანი აქვს და, ე.ი. ნიუტონის მეორე კანონის თანახმად ჰარმონიული რხევის გამომწვევი ძალა ყოველთვის მიმართულია წონასწორობის მდებარეობისაკენ (\(x=0\) ).
ნახ. 4–ზე მოყვანილია ჰარმონიული რხევისას სხეულის კოორდინატის, სიჩქარისა და აჩქარების გრაფიკები.
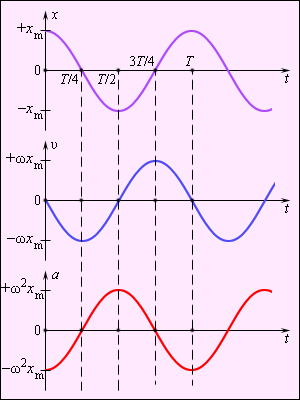
ნახ. 4.
ჰარმონიულად მერხევი სხეულის კოორდინატის \(x(t)\), სიჩქარის \(v(t)\) და აჩქარების \(a(t)\) გრაფიკები.