{loadnavigation}

საზოგადოდ თანაბარაჩქარებული მოძრაობას ისეთ მოძრაობას უწოდებენ, რომლის დროსაც აჩქარების ვექტორი უცვლელია როგოც სიდიდით ასევე მიმართულებით. ასეთ მოძრაობის მაგალითს წარმოადგენს ჰორიზონტისადმი გარკვეული კუთხით ნასროლი ქვის მოძრაობა (ჰაერის წინააღმდეგობის გათვალისწინების გარეშე). ტრაექტორიის ნებისმიერ წერტილში ქვის აჩქარება თავისუფალი ვარდნის აჩქარების  ტოლია. ქვის მოძრაობის კინემატიკური აღწერისათვის მოსახერხებელია კოორდინატთა სისტემა ისე შეირჩეს, რომ OY ღერძი აჩქარების ვექტორის პარალელური იყოს. მაშინ ქვის მრუდწირული მოძრაობა შეიძლება წარმოვადგინოთ ორი – OY ღერძის გასწვრივ წრივი თანაბარაჩქარებული მოძრაობისა და OX ღერძის გასწვრივ წრივი თანაბარი მოძრაობის  ჯამი სახით (ნახ. 1.) .

ამგვარად, თანაბარაჩქარებული მოძრაობის შესწავლა დაიყვანება წრფივი თანაბარაჩქარებული მოძრაობის შესწავლამდე. წრფივი მოძრაობის შემთხვევაში  სიჩქარისა და  აჩქარების ვექტორები მიმართულია მოძრაობის მიმართულების გასწვრივ. ამიტომ  მოძრაობის მიმართულებაზე v სიჩქარის და a აჩქარების პროექციები შეიძლება ალგებრულ სიდიდეებად განვიხილოთ.

ნახ. 1.
 სიჩქარის და  აჩქარების ვექტორების პროექციები კოორდინატთა ღერძზე :  a_x = 0, a_y = –g

წრივი თანაბარაჩქარებული მოძრაობაის დროს სხეულის სიჩქარე განისაზღვრება ფორმულით 

v = v₀ + at.                  (*)

ამ ფორმულაში v₀ სხეულის სიჩქარეა t = 0 მომენტში (საწყისი სიჩქარე), a = const – აჩქარებაა. სიჩქარის გარაფიკზე  v (t) ფუნქციას წრფის სახე აქვს (ნახ. 2).

ნახ. 2.
თანაბარაჩქარებული მოძრაობის სიჩქარის გრაფიკები.

სიჩქარის გრაფიკის დახრის მიხედვით შეიძლება განისაზღვროს სხეულის a აჩქარება. ნახ. 2. წარმოდგენილია შესაბამისი გრაფიკები. I გრაფიკისათვის აჩქარება რიცხობრივად ABC სამკუთხედის გვედების ფარდობის ტოლია:

რაც მეტია სიჩქარის გრაფიკის მიერ დროის ღერძთან შექმნილი კუთხე β, მით მეტია აჩქარება.
გრაფიკი I-სათვის: v₀ = –2 მ/წმ, a = 1/2 მ/წმ².
გრაფიკი I I -სათვის: v₀ = 3 მ/წმ, a = –1/3 მ/წმ².
სიჩქარის გრაფიკი საშუალებას იძლევა, აგრეთვე განისაზღვროს გარკვეული t დროის განმავლობაში სხეულის გადაადგილების sპროექცია. დროის ღერძზე გამოიყოს მცირე დროის გარკვეული ინტერვალი Δt. თუ ეს ინტერვალი საკმარისად მცირეა, სიჩქარის ცვლილებაც ამ ინტერვალში არ იქნება დიდი, ე.ი. მოძრაობა ამ ინტერვალში შეიძლება ჩაითვალოს თანაბრად  რაღაც საშუალო სიჩქარით, რომელიც ტოლია სხეულის მყისიერი v სიჩქარისა Δt ინტერვალის შუაში. აქდან გამომდინარე, Δs გადაადგილება Δt  დროში ტოლია Δs = vΔt. ეს გადაადგილება დაშტრიხული სიბრტყის ფართობის (ნახ. 2.) ტოლია. თუ დროს 0–დან t–მდე დავყოფთ მცირე Δt ინტერვალებად, მივიღებთ, რომ s გადაადგილება t დროში წრფივი თანაბრადაჩქარებული მოძრაობის დროს ტოლია ODEF ტრაპეციის ფართობისა. შესაბამისადაა შესრულებული აგებები გრაფიკი I I -სათვის. T დრო მიღებულია 5,5წმ–ს ტოლად.

რადგანაც v – v₀ = at, თანაბრადაჩქარებული მოძრაობისას s გადააგილების გამოსათვლელ ფორმულას დროის 0–დან t–მდე ინტერვალისათვის აქვს სახე:

                                        (**)

სხეულის y კოორდინატის საპოვნელად ნებისმიერ საჭირო  t მომენტში საჭიროა საწყის  y₀ კოორდინატს დაემატოს გადაადგილება  t მომენტისათვის:

                                         (***)

ამ გამოსახულებას თანაბარაჩქარებული მოძრაობის კანონი ეწოდება.
თანაბარაჩქარებული მოძრაობის ანალიზის დროს, ხანდახან წარმოიშვება სხეულის გადაადგილების განსაზღვის საჭიროება ცნობილი საწყისი v₀ და v საბოლოო სიჩქარეებისა და a აჩქარების შემთხვევაში. ასეთი ამოცანა შეიძლება ამოიხსნას ზემოთ აღწერილი განტოლებიდან t დროის გამორიცხვით, რის შედეგადაც მიიღება

ამ ფორმულიდან შეიძლება v  საბოლოო სიჩქარის განსასაძღვრი ფორმულის მიღება თუ ცნობილია საწყისი v₀ სიჩქარე, a აჩქარება და სხეულის გადაადგილება s.

თუ საწყისი v₀ სიჩქარე ნულის ტოლია, ამ ფორმულებს აქვს სახე:

კიდევ ერთხელ მივაქციოთ ყურადღება იმას, რომ წრფივი თანაბრადაჩქარებული მოძრაობის ფორმულებში შემავალი სიდიდეები v₀, v, s, a, y₀  ალგებრულ სიდიდეებს წარმოსდგენენ. კონკრეტული მოძრაობის სახის მიხედვით მათ შეუძლიათ მიიღონ როგორც დადებითი, ისე უარყოფითი მნიშვნელობები.

{loadnavigation}

მაქანიკური მოძრაობის უმარტივეს სახეს წარმოადგენს სხეულის წრფივი მოძრაობა მუდმივი სიდიდისა (მოდულის) და მიმართულების მქონე სიჩქარით. ასეთ მოძრაობას თანაბარი მოძრაობა ეწოდება. თანაბარი მოძრაობის დროს სხეული დროის ნებისმიერ ტოლ შუალედში ტოლ მანძილს გადის. თანაბარი წრფივი მოძრაობის კინემატიკური აღწერისათვის კოორდინატთა სისტემის ღეძი მოსახერხებელია მოძრაობის მიმართულებას ემთხვეოდეს. თანაბარი მოძრაობის დროს სხეულის მდებარეობა განისზღვრება მხოლოდ ერთი – x  კოორდინატის მითითებით. გადაადგილებისა და სიჩქარის ვექტორები  ყოველთვის კოორდინატთა OX ღეძის პარალელურებია. ამიტომ წრფივი მოძრაობის დროს  შეიძლება გადაადგილების და სიჩქარის პროექცირება  OX ღეძზე და ამ პროქციების ალგებრულ სიდიდეებად განხილვა.
თუ სხეული დროის რაღაც გარკვეულ t₁ მომენტში იმყოფებოდა x₁  წერტილში, ხოლო მოგვიანებით t₂ მომენტში – წერტილში კოორდინატით x₂, მაშინ გადაადგილების პროექცია Δs OX ღერძზე Δt = t₂ – t₁ დროში, ტოლია

Δs = x₂ – x₁.

სხეულის მოძრაობის მიმართულებიდან გამომდინარე ეს სიდიდე შეიძლება იყოს დადებითიც და უაყოფითიც. თანაბარი წრფივი მოძრაობისას გადაადგილების მოდული განვლილი მანძილის ტოლია.
თანაბარი წრფივი მოძრაობის სიჩქარე გამოისახება ფარდობით

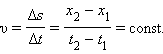
თუ v > 0, მაშინ ხსეული OX ღერძის დადებითი მიმართულებით მოძრაობს; როცა v < 0 – სხეული საწინააღმდეგო მიმართულებით მოძრაობს.
 თანაბარი წრფივი მოძრაობისას x კოორდინატის დამოკიდებულება t დროზე (მოძრაობის კანონი) წრფივი ალგებრული განტოლებით განისაზღვრება:

x (t) = x₀ + vt.

ამ განტოლებაში v = const – სხეულის მოძრაობის სიჩქარეა, x₀ - იმ წერტილის კოორდინატი, რომელშიც სხეული დროის t = 0 მომენტში მდებარეობს. მოძრაობის კანონის გრაფიკი x(t) წრფეს წარმოადგენს. ასეთი გრაფიკების მაგალითები 1. ნახაზზეა მოცემული.

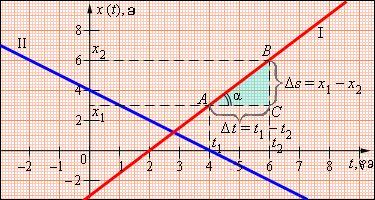
ნახ.1.
თანაბარი წრფივი მოძრაობის გრაფიკი

ნახაზი 1. I გრაფიკზე გამოსახული მოძრაობის კანონისათვის, როცა t = 0 სხეული იმყოფება წერტილში კოორდინატით x0 = –3. t1 = 4 და t2 = 6 დროის მომენტებს შორის სხეული გადაადგილდა x1 = 3 მ წერტილიდან x2 = 6 მ წერტილში.  Δt = t2 – t1 = 2 დროის განმავლობაში სხეული გადაადგილდა Δs = x2 – x1 = 3 მეტრით. ე.ი. სხეულის სიჩქარე ტოლია

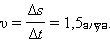
მიღებული სიჩქარე დადებითი სიდიდე აღმოჩნდა. ეს ნიშნავს, რომ სხეული OX ღერძის დადებითი მიმართულებით მოძრაობდა. მივაქციოთ ყურადღება იმ გარამოებას, რომ გრაფიკზე სხეულის სიჩქარე გეომეტრიულად განისაზღვრება როგორც ABC სამკუთხედის BC და AC გვერდების ფარდობა (ნახ.1.)

რაც უფრო მეტია ამ წრფის მიერ დროის ღერძთან შედგენილი α კუთხე, ე.ი. რაც მეტია გრაფიკის დახრა, მით მეტია სხეულის სიჩქარე. ამბობენ ხოლმე, რომ სხეულის სიჩქარე ტოლია x (t) წრფის დახრის α  კუთხის ტანგენსისა. მათემატიკური თვალსაზრისით ეს გამოთქმა მაინცდამაინც კორექტული ვერ არის, რადგანაც ABC სამკუთხედის BC და AC გვერდებს სხვადასვა განზომილება გააჩნიათ: BC  იზომება მეტრებში. AC კი წამებში.
ანალოგიურად. ნახაზი 1. II გრაფიკისათვის  x₀ = 4 მ, v = –1 მ/წმ. ნახ.2.–ზე სხეულის მოძრაობის კანონი x (t) გამოსახულია წრფის მონაკვეთების საშუალებით. სხეულის ასეთ მოძრაობა წირის გასწვრივ არაა თანაბარი. გრაფიკის სხვადასხვა მონაკვეთზე სხეული სხვადასხვა სიჩქარით მოძრაობს. თითოეული მონაკვეთზე სიჩქარე შეიძლება განისაზღვროს ამ მონაკვეთის დროის ღერძისადმი დახრის მიხედვით. გრაფიკის გარდატეხის წერტილებში სხეული მყისიერად იცვლის სიჩქარეს. გრაფიკზე (ნახ. 2.) ეს ხდება t₁ = –3 წმ, t₂ = 4 წმ, t₃ = 7 წმ და t₄ = 9 წმ–ზე. მოძრაობის გრაფიკის მიხედვით რთული არაა იმის განსაზღვრა, რომ (t2; t1) ინტერვალში სხეული მოძრაობს v12 = 1 მ/წმ სიჩქარით, (t₃; t₂) –   v₂₃ = –4/3 მ/წმ სიჩქარით და (t₄; t₃) –  v₃₄ = 4 მ/წმ სიჩქარით.
უნდა აღინიშნოს რომ, სხეულის ამგვარი (მონაკვეთებით შედგენილი) მოძრაობის კანონის შემთხვევაში, გავლილი მანძილი l არ ემთხვევა გადაადგილებას s. მაგალითად, მოცემულ ნახაზზე სხეულის გადაადგილება 0-დან 7–მდე ტოლია ნულის (s = 0). ამ დროის განმავლობაში სხეულის მიერ განვლილი  l = 8 მ.

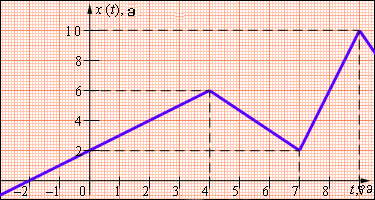
ნახ. 2.

{loadnavigation}

სხეულის მოძრაობა შეიძლება აღიწეროს ათვლის სხვადასხვა  სისტემაში. კინემატიკის თვალთახედვით ათვლის ყველა სისტემა თანაბარუფლებიანია, თუმცა მოძრაობის კენემატიკური მახასიათებლები, ისეთი როგორიცაა ტრაექტორია, გადაადგილება, სიჩქარე, სხვადასხვა სისტემაში  განსხვავებული აღმოჩნდება. სიდიდეებს, რომლებიც ათვლის სისტემის არჩევაზეა დამოკიდებული, ფარდობითი ეწოდებათ.
დავუშვათ გვაქვს ათვლის ორი სისტემა. სისტემა XOY პირობითად ითვლება უძრავად, ხოლო X'O'Y 'მოძრაობს გადატანითად XOY–ის  მიმართ \(\vec{v}_{0}\) \(\vec{v}_{0}\) სიჩქართ.  XOY სისტემა შეიძლება დაკავშრებული იყოს, მაგალითდ დედამიწასთან, ხოლო X'O'Y– რელსებზე მოძრავ პლატფორმასთან.

ნახაზი 1.
გადაადგილების შეკრება ათვლის სხვადასხვა სისტემის მიმართ.

ვთქვათ, ადამიანი გადავიდა პლატფორმაზე A წერტილიდან B წერტილში გარკვეულ დროში. მაშინ მისი გადაადგილება პლატფორმის მიმართ შეესაბამება \(\vec{{s}'}\) ვექტორს, ხოლო პლატფორმის გადაადგილება დედამიწის მიმართ \(\vec{s}_{0}\) ვექტორს. 1. ნახაზიდან ჩანს, რომ ადამიანის გადაადგილება დედამიწის მიმართ იქნება  \(\vec{s}\) ვექტორის შესაბამისი, რომელიც წარმოადგენს \(\vec{s}_{0}\) და \(\vec{s}^{{\color{White}'}'}\) ვექტორების ჯამს.

\(\vec{s}=\vec{s}_{0}+\vec{s}^{{\color{White}'}'}\)

იმ შემთხვევაში, როცა ათვლის სისტემებიდან ერთი მეორეს მიმართ მოძრაობს გადატანითად  (იხ. 1 ნახაზი) \(\vec{v}_{0}\) მუდმივი სიჩქარით, ეს გამოსახულება ღებულობს სახეს:

\(\vec{s}=\vec{v}_{0}\Delta t+\vec{s}^{{\color{White}'}'}\)

თუ განვიხილავთ გადაადგილებას დროის მცირე  Δt შუალედში , მაშინ თუ ამ განტოლების ორივე ნაწილს გავყოფთ Δt–ზე და  გადავალთ ზღვარზე, როცა Δt → 0 მივიღებთ 

\(\vec{v}=\vec{v}_{0}+\vec{v}^{{\color{White}'}'}\)                                                                    (*)

სადაც, \(\vec{v}\) – სხეულის სიჩქარეა „უძრავ“   XOY ათვლის სისტემაში, \(\vec{v}^{{\color{White}'}'}\) – სხეულის სიჩქარე „მოძრავ“X'O'Y' ათვლის სისტემაში. \(\vec{v}\) და \(\vec{v}^{{\color{White}'}'}\) სიჩქარეებს  ხანდახან პირობითად აბსოლუტურ და ფარდობით სიჩქარეებს უწოდებენ; ხოლო \(\vec{v}_{0}\) სიჩქარეს – გადატანით სიჩქარეს.
(*) ფორმულას სიჩქარეთა შეკრების კლასიკურ კანონს უწოდებენ.
სხეულის აბსოლუტური სიჩქარე  \(\vec{v}\)  მისი ფარდობითი საჩქარისა \(\vec{v}^{{\color{White}'}'}\) და მოძრავი ათვლის  სისტემის გადატანითი \(\vec{v}_{0}\) სიჩქარის ვექტორული ჯამის ტოლია.

საყურადღებოა  სხეულის აჩქარებების საკითხი სხვადასხვა ათვლის  სისტემში. (*)-დან  გამომდინარეობს, რომ თუ ათვლის სიტემები ერთმანეთის მიმართ თანაბარად და წრფივად მოძრაობენ სხეულის აჩქარება ამ ორ სისტემაში ერთნაირია, ე.ი. \(\vec{a}=\vec{a}^{{\color{White}'}'}\) . მართლაც, თუ \(\vec{v}_{0}\) – ვექტორის სიდიდე და მიმართულება  დროში უცვლელი რჩება, მაშინ სხეულის ფარდობითი სიჩქარის ნებისმიერი ცვლილება \(\Delta \vec{v}^{{\color{White}'}'}\) დაემთხვევა  მისი აბსოლუტური სიჩქარის  ცვლილებას \(\Delta \vec{v}\)-ს

შესაბამისად, 

\(\frac{\Delta \vec{v}}{\Delta t}=\frac{\Delta \vec{v}^{{\color{White}'}'}}{\Delta }\)

როცა Δt → 0, მივიღებთ \(\vec{a}=\vec{a}^{{\color{White}'}'}\).
ზოგადად, ერთმანეთის მიმარათ აჩქარებულად მოძრავ ათვლის სიტემაში სხეულის აჩქარება განსხვავებულია.
იმ შემთხვევაში, როცა ფარდობითი სიჩქარის \(\vec{v}^{{\color{White}'}'}\) ვექტორი და გადატანითი სიჩქარის \(\vec{v}_{0}\)  ვექტორი ერთმანეთის მიმართ პარალელურია, სიჩქარეთა შეკრების კანონი შეიძლება ჩაიწეროს სკალარული ფორმით:

υ = υ₀ + υ'.

ამ შემთხვევაში ყველა მოძრაობა ხდება ერთი სწორი ღერძის გასწვრივ (მაგალითად, OX ღერძის). სიჩქარეები υ, υ0  და υ'  განიხილება როგორც  აბსოლუტური, გადატანითი და ფარდობითი სიჩქარეების პროექციები OX ღერძზე. ისინი  ალგებრულ სიდიდებს წარმოადგენენ და შესაბამისად, მათ უნდა დაეწეროთ განსაზღვრული ნიშნები (პლუსი ან მინუსი) მოძრაობის მიმართულებიდან გამომდინარე.