მაქანიკური მოძრაობის უმარტივეს სახეს წარმოადგენს სხეულის წრფივი მოძრაობა მუდმივი სიდიდისა (მოდულის) და მიმართულების მქონე სიჩქარით. ასეთ მოძრაობას თანაბარი მოძრაობა ეწოდება. თანაბარი მოძრაობის დროს სხეული დროის ნებისმიერ ტოლ შუალედში ტოლ მანძილს გადის. თანაბარი წრფივი მოძრაობის კინემატიკური აღწერისათვის კოორდინატთა სისტემის ღეძი მოსახერხებელია მოძრაობის მიმართულებას ემთხვეოდეს. თანაბარი მოძრაობის დროს სხეულის მდებარეობა განისზღვრება მხოლოდ ერთი – x კოორდინატის მითითებით. გადაადგილებისა და სიჩქარის ვექტორები ყოველთვის კოორდინატთა OX ღეძის პარალელურებია. ამიტომ წრფივი მოძრაობის დროს შეიძლება გადაადგილების და სიჩქარის პროექცირება OX ღეძზე და ამ პროქციების ალგებრულ სიდიდეებად განხილვა.
თუ სხეული დროის რაღაც გარკვეულ t1 მომენტში იმყოფებოდა x1 წერტილში, ხოლო მოგვიანებით t2 მომენტში – წერტილში კოორდინატით x2, მაშინ გადაადგილების პროექცია Δs OX ღერძზე Δt = t2 – t1 დროში, ტოლია
Δs = x2 – x1.
სხეულის მოძრაობის მიმართულებიდან გამომდინარე ეს სიდიდე შეიძლება იყოს დადებითიც და უაყოფითიც. თანაბარი წრფივი მოძრაობისას გადაადგილების მოდული განვლილი მანძილის ტოლია.
თანაბარი წრფივი მოძრაობის სიჩქარე გამოისახება ფარდობით
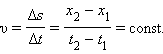
თუ v > 0, მაშინ ხსეული OX ღერძის დადებითი მიმართულებით მოძრაობს; როცა v < 0 – სხეული საწინააღმდეგო მიმართულებით მოძრაობს.
თანაბარი წრფივი მოძრაობისას x კოორდინატის დამოკიდებულება t დროზე (მოძრაობის კანონი) წრფივი ალგებრული განტოლებით განისაზღვრება:
x (t) = x0 + vt.
ამ განტოლებაში v = const – სხეულის მოძრაობის სიჩქარეა, x0 - იმ წერტილის კოორდინატი, რომელშიც სხეული დროის t = 0 მომენტში მდებარეობს. მოძრაობის კანონის გრაფიკი x(t) წრფეს წარმოადგენს. ასეთი გრაფიკების მაგალითები 1. ნახაზზეა მოცემული.
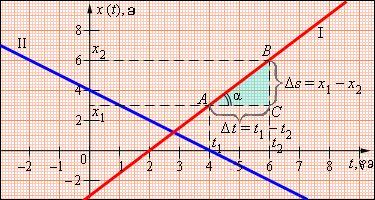
ნახ.1.
თანაბარი წრფივი მოძრაობის გრაფიკი
ნახაზი 1. I გრაფიკზე გამოსახული მოძრაობის კანონისათვის, როცა t = 0 სხეული იმყოფება წერტილში კოორდინატით x0 = –3. t1 = 4 და t2 = 6 დროის მომენტებს შორის სხეული გადაადგილდა x1 = 3 მ წერტილიდან x2 = 6 მ წერტილში. Δt = t2 – t1 = 2 დროის განმავლობაში სხეული გადაადგილდა Δs = x2 – x1 = 3 მეტრით. ე.ი. სხეულის სიჩქარე ტოლია
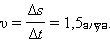
მიღებული სიჩქარე დადებითი სიდიდე აღმოჩნდა. ეს ნიშნავს, რომ სხეული OX ღერძის დადებითი მიმართულებით მოძრაობდა. მივაქციოთ ყურადღება იმ გარამოებას, რომ გრაფიკზე სხეულის სიჩქარე გეომეტრიულად განისაზღვრება როგორც ABC სამკუთხედის BC და AC გვერდების ფარდობა (ნახ.1.)

რაც უფრო მეტია ამ წრფის მიერ დროის ღერძთან შედგენილი α კუთხე, ე.ი. რაც მეტია გრაფიკის დახრა, მით მეტია სხეულის სიჩქარე. ამბობენ ხოლმე, რომ სხეულის სიჩქარე ტოლია x (t) წრფის დახრის α კუთხის ტანგენსისა. მათემატიკური თვალსაზრისით ეს გამოთქმა მაინცდამაინც კორექტული ვერ არის, რადგანაც ABC სამკუთხედის BC და AC გვერდებს სხვადასვა განზომილება გააჩნიათ: BC იზომება მეტრებში. AC კი წამებში.
ანალოგიურად. ნახაზი 1. II გრაფიკისათვის x0 = 4 მ, v = –1 მ/წმ. ნახ.2.–ზე სხეულის მოძრაობის კანონი x (t) გამოსახულია წრფის მონაკვეთების საშუალებით. სხეულის ასეთ მოძრაობა წირის გასწვრივ არაა თანაბარი. გრაფიკის სხვადასხვა მონაკვეთზე სხეული სხვადასხვა სიჩქარით მოძრაობს. თითოეული მონაკვეთზე სიჩქარე შეიძლება განისაზღვროს ამ მონაკვეთის დროის ღერძისადმი დახრის მიხედვით. გრაფიკის გარდატეხის წერტილებში სხეული მყისიერად იცვლის სიჩქარეს. გრაფიკზე (ნახ. 2.) ეს ხდება t1 = –3 წმ, t2 = 4 წმ, t3 = 7 წმ და t4 = 9 წმ–ზე. მოძრაობის გრაფიკის მიხედვით რთული არაა იმის განსაზღვრა, რომ (t2; t1) ინტერვალში სხეული მოძრაობს v12 = 1 მ/წმ სიჩქარით, (t3; t2) – v23 = –4/3 მ/წმ სიჩქარით და (t4; t3) – v34 = 4 მ/წმ სიჩქარით.
უნდა აღინიშნოს რომ, სხეულის ამგვარი (მონაკვეთებით შედგენილი) მოძრაობის კანონის შემთხვევაში, გავლილი მანძილი l არ ემთხვევა გადაადგილებას s. მაგალითად, მოცემულ ნახაზზე სხეულის გადაადგილება 0-დან 7–მდე ტოლია ნულის (s = 0). ამ დროის განმავლობაში სხეულის მიერ განვლილი l = 8 მ.
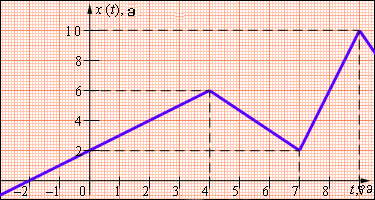
ნახ. 2.


