თუ ჩაკეტილი მექანიკური სისტემის სხეულები ურთიერთქმედებენ მხოლოდ მიზიდულობისა და დრეკადობის ძალების საშუალებით, მაშინ მათ მიერ შესრულებული მუშაობა, აღებული საწინააღმდეგო ნიშნით, ამ სხეულების პოტენციური ენერგიის ცვლილების ტოლია:
\(A=-(E_{p2}-E_{p1})\).
კინეტიკური ენერგიის თეორემის მიხედვით, ეს მუშაობა სხეულების კინეტიკური მუშაობის ცვლილების ტოლია:
\(A=E_{k2}-E_{k1}.\)
აქედან გამომდინარე:
\(E_{k2}-E_{k1}=-(E_{p2}-E_{p1})\Rightarrow E_{k1}+E_{p1}=E_{k2}+E_{p2}.\)
ჩაკეტილი მექანიკური სისტემის შემადგენელი და მიზიდულობისა და დრეკადობის ძალების საშუალებით ურთიერთქმედი სხეულების კინეტიკური და პოტენციური ენერგიების ჯამი უცვლელი რჩება.
ეს ფორმულირება მექანიკური პროცესებში ენერგიის მუდმივობის კანონს წარმოადგებს. ის ნიუტონის კანონების შედეგია. \(E=E_{k}+E_{p}\) ჯამს სრულ მექანიკურ ენერგიას უწოდებენ. მექანიკური ენერგიის მუდმივობის კანონი მხოლოდ მაშინ სრულდება, როცა სხეულები, ჩაკეტილ სისტემაში ურთიერთქმედებენ მხოლოდ კონსერვატული ძალებით, ე.ი. ძალებით რომელთათვისაც პოტენციური ენერგიის ცნების შემოღებაა შესაძლებელი.
ენერგიის შენახვის კანონის გამოყენების მაგალითია, იმ უჭიმვადი ძაფის მინიმალური სიმტკიცის პოვნა, რომელიც იჭერს მის ბოლოზე დამაგრებულ მასის სხეულს ბრუნვის ვერტიკალურ სიბრტყეში (ე.წ. ჰიუგენსის ამოცანა). ნახ. 1–ზე მოცემულია ამ ამოცანის განმარტება.
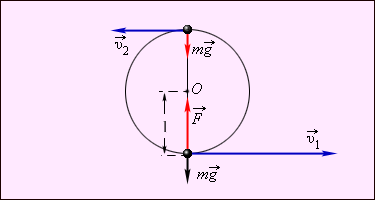
ნახ. 1.
ჰიუგენსის ამოცანა. \(\vec{F}\) – ძაფის დაჭიმულობის ძალა ტრაექტორიის ქვედა წერტილში
ენერგიის მუდმივობის კანონი სხეულისთვის ტრაექტორიის ქვედა და ზედა წერტილებში შემდეგი სახით ჩაიწერება:
\(\frac{mv_{1}^{2}}{2}=\frac{mv_{2}^{2}}{2}+mg2l.\)
ყურადღება მივაქციოთ იმას, რომ ძაფის დაჭიმულობის \(\vec{F}\) ძალა ყოველთვის სხეულის სიჩქარის მართობულია; ამიტომ ის მუშაობას არ ასრლებას.
ბრუნვის მინიმალირი სიჩქარისას ძაფის დაჭიმულობა ტრაექტორიის ზედა წერტილში ნულის ტოლია და, ე.ი. ცენტრისკენული აჩქარება სხეულს ენიჭება მხოლოდ სიმძიმის ძალის გავლენით:
\(\frac{mv_{2}^{2}}{l}=mg.\)
ამ დამოკიდებულებებიდან გამოდის:
\(v_{1\: min}^{2}=5gl.\)
ცენტრისკენული აჩქარება ტრაექტორიის ქვედა წერტილში განპირობებულია სხვადასხვა მხარეს მიმართული \(\vec{F}\) და \(m\vec{g}\) ძალებით:
\(\frac{mv_{1}^2}{2}=F-mg.\)
აქედან გამოდის, რომ სხეულის ზედა წერტილში მინიმალური სიჩქარის დროს ძაფის დაჭიმულობა ქვედა წერტილში მოდულით ტოლია
%F=6mg.$
ნათელია, რომ ძაფის სიმტკიცე ამ სიდიდეს უნდა აღემატებოდეს.
ძალიან მნიშვნელოვანია აღინიშნოს, რომ მექანიკური ენერგიის შენახვის კანონი სხეულის ტრაექტორიის ორ განსხვავებულ წერტილში მისი კოორდინატებსა და სიჩქარეებს შორის კავშირის მიღების საშუალებას იძლევა, ტრაექტორიის ყველა სხვა წერტილში სხეულის მოძრაობის კანონის ანალიზის გარეშე. მექანიკური ენერგიის შენახვის კანონის გამოყენაბას შეუძლია საგრძნობლად გაადვილოს მრავალი ამოცანის ამოხსნა.
რეალურ პირობებში კონსერვატული ძალების გვერდით ყოველთვის მოქმედებენ ხახუნის ან გარემოს წინააღმდეგობის ძალები.
ხახუნის ძალა არაა კონსერვატული, მისი მუშაობა განვლილი მანძილის სიგრძეზეა დამოკიდებული.
თუ ჩაკეტილი სისტემის სხეულებს შორის მოქმედებს ხახუნის ძალები, მაშინ მექანიკური ენერგია არ ინახება. მექანიკური ენერგიის ნაწილი სხეულების შინაგან ენერგიად გადაიქცევა (გათბობა).
ეს, ექსპერიმენტულად გადგენილი ფაქტი გამოხატავს ბუნების ფუნდამენტურ კანონს – ენერგიის შენახვისა და გარდაქმნის კანონს.
ენერგიის შენახვისა და გარდაქმნის კანონის ერთ–ერთ შედეგს წარმოადგებს „მუდმივი ძრავის“ (perpetuum mobile) შექმნის შეუძლებლობა – მანქანისა, რომელიც, ენერგიის დანახარჯის გარეშე, განუსაზღვრელად დიდი ხნის განმავლობაში შეძლებდა მუშაობის შესრულებას (ნახ. 2).
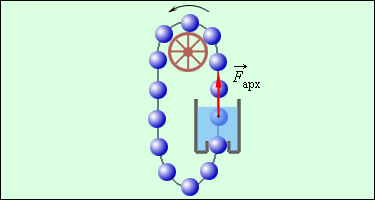
ნახ. 2.
„მუდმივი ძრავის“ ერთ–ერთი პროექტი. რატომ არ იმუშავებს ეს მანქანა?
ისტორია „მუდმივი ძრავის“ არა ერთ პროექტს ინახავს. ზოგ მათგანში „გამომგონებლის“ შეცდომა თვალნათლივ ჩანს, სხვებში ხელსაწყოს რთული კონსტრუქციის მიღმაა დაფარული და ხშირად ძნელი გასაგებია რატომ არ მუშაობს ეს მანქანა. „მუდმივი ძრავის“ შექმნის უნაყოფო ცდები ჩვენს დროშიც გრძელდება. ყველა ისინი მარცხისთვის არიან განწირულნი, რადგან ენერგიის შენახვისა და გარდაქმნის კანონი ენერგიის დახარჯვის გარეშე მუშაობის მიღებას „კრძალავს“.


