მყარ სხეულებში – ამორფულშიც და კრისტალურშიც – ნაწილაკები (მოლეკულები, ატომები, იონები) ასრულებენ სითბურ რხევას წონასწორობის მახლობლად, სადაც მათი ურთიერთქმედების ენერგია მინიმალურია. ნაწილაკებს შორის მანძილის გაზრდისას აღიძვრება მიზიდულობის ძალები, შემცირებისას – განზიდვის ძალები. ნაწილაკებს შორის ურთიერთქმედების ძალები განსაზღვრავენ მყარი სხეულის მექანიკურ თვისებებს.
მყარი სხეულის დეფორმაცია გარე ძალების მოქმედებით მყარი სხეულის ნაწილაკებს შორის განლაგებისა და მანძილების ცვლილების შედეგია.

დეფორმაციის რამოდენიმე სახე არსებობს. ზოგი მათგანი წარმოდგენილია ნახ. 1-ზე.
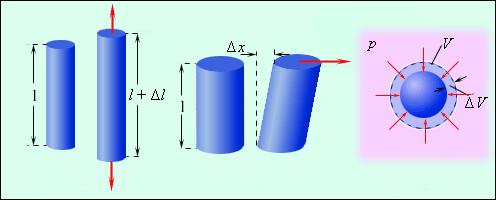
ნახ. 1.
მყარი სხეულებისდეფორმაციის ზოგიერთი სახე: 1 – გაჭიმვის დეფორმაცია; 2 – წანაცვლების დეფორმაცია; 3 – ყოველმხრივი გაჭიმვის დეფორმაცია
დეფორმაციის უმარტივეს სახეს გაჭიმვის დეფორმაცია წარმოადგენს. იგი შეიძლება დავახასიათოთ, როგორც \(\vec{F}\) გარე ძალის მოქმედებით წარმოქმნილი აბსოლუტური \(\Delta l\) წაგრძელება ან შეკუმშვა. \(\Delta l\) და \(F\) შორის კავშირი დამოკიდებულია არა მარტო ნივთიერების მექანიკურ თვისებებზე, არამედ სხეულის გეომეტრიულ ზომებზეც (სისქესა და სიგრძეზე).
აბსოლუტური \(\Delta l\) წაგრძელების შეფარდებას ნიმუშის საწყის \(l\) სიგრძესთან \(\varepsilon\)-ს ფარდობით წაგრძელებას ან ფარდობით დეფორმაციას უწოდებენ
\(\varepsilon =\frac{\Delta l}{l}.\)
გაჭიმვისას \(\varepsilon >0\), შეკუმშვისას \(\varepsilon <0\).
თუ გამჭიმავი გარე ძალის მიმართულებას დადებითად მივიღებთ, მაშინ \(F>0\) გაჭიმვის დეფორმაციისთვის და \(F<0\) – შეკუმშვისათვის. გარე ძალის \(F\) ფარდობას სხეულის განივკვეთის \(S\) ფართობთან მექანიკურ დაძაბულობას უწოდებენ:
\(\sigma=\frac{F}{S}.\)
მექანიკური დაძაბულობის ერთეულად \(Si\) სიტემაში მიღებულია პასკალი. მექანიკური დაძაბულობა წნევის ერთეულებში იზომება.
\(\varepsilon\) და \(\sigma\) სიდიდეებს შორის დამოკიდებულება მყარი სხეულების მექანიკური თვისებების ერთერთ უმნიშვნელოვანეს მახასიათებელს წარმოადგენს. ამ დამოკიდებულების გრაფიკს გაჭიმვის დიაგრამას უწოდებენ. აბსცისთა ღეძზე აღებულია ფარდობითი წაგრძელება \(\varepsilon\), ორდანატაზე – მექანიკური დაძაბულობა \(\sigma\). ნახ. 2-ზე წარმოდგენილია გაჭიმვის დიაგრამის ტიპური მაგალითი მეტალებისთვის (სპილენძი და რბილი რკინა).
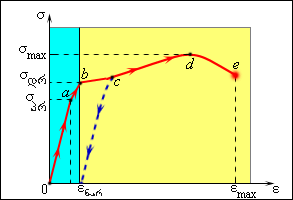
ნახ. 2.
პლასტიკური მასალის ტიპური გაჭიმვის დიაგრამის. ცისფერი ზოლი - დრეკადი დეფორმაციის არეა
მცირე (1 %-ზე საგრძნობლად ნაკლები) დეფორმაციებისთვის \(\sigma\) და \(\varepsilon\) კავშირი წრფივია (Oa მონაკვეთი დიაგრამაზე). ამ შემთხვევაში დაძაბულობის მოხსნისას დეფორმაცია ქრება. ასეთ დეფორმაციას დრეკადს უწოდებენ. σ = σპრ მაქსიმალური მნიშვნელობა, რომლისათვისაც წრფივი კავშირი არ ირღვევა \(\sigma\) და \(\varepsilon\) შორის, პროპორციულობის ზღვარს უწოდებენ (a წერტილი). წრფივ უბანზე სრულდება ჰუკის კანონი:
\(\varepsilon=\frac{1}{E}\sigma.\)
\(E\) კოეფიციენტს იუნგის მოდულს უწოდებენ.
დაძაბულობის შემდგობი გადიდებისას \(\sigma\) და \(\varepsilon\) – ს შორის კავშირი არაწრფივია (ab უბანი). დაძაბულობის მოხსნისას დეფორმაცია პრაქტიკულად მთლიანად ქრება, ე.ი. სხეული აღიდგენს თავის ზომებს. მაქსიმალურ დაძაბულობას ამ უბანზე ზღვრული დრეკადობა ეწოდება. თუ σ > σდაჭ, მაშინ დაძაბულობის მოხსნის მერე ნიმუში საწყის ზომებს ვერ აღიდგენს და სხეული ინარჩუნებს ნარჩენ დეფორმაციას. ასეთ დეფორმაციას პლასტიკურს უწოდებენ (bc, cd და de უბნები). bc უბანზე დეფორმაცია თითქმის დაძაბულობის გაზრდის გარეშე ხდება. ამ მოვლენას მასალის დენადობა ეწოდება. d წერტილში ის უდიდესი დაძაბულობა σmax მიიღწევა, რომელსაც მოცემულ მასალას შეუძლია გაუძლოს (სიმტკიცის ზღვარი). e წერტილში მასალის რღვება ხდება. იმ მასალებს, რომლებისთვისაც გაჭიმვის დიაგრამას აქვს ნახ. 2 სახე პლასტიკურს უწოდებენ. ასეთი მასალების ჩვეულებრივი εmax დეფორმაცია, რომლის დროსაც მასალის რღევა ხდება ათეულობით აღემატება დრეკადი დეფორმაციის უბნის სიგანეს. ასეთ მასალებს მრავალი მეტალი მიეკუთვნება.
იმ მასალებს, რომლებისთვისაც რღვევა ხდება როცა დეფორმაცია დრეკადი დეფორმაციის უბანს ოდნავ აჭარბებს, მყიფეს უწოდებენ (მინა, ფაიფური, თუჯი).
ანალოგიურ კანონზომიერებას ემორჩილება წანაცვლების დეფორმაციაც (ნახ. 1(2)). ამ შემთხვევაში ძალის ვექტორი \(\vec{F}\)მიმართულია ნიმუშის მხების გასწვრივ. ფარდობითი დეფორმაცია განისაზღვრება უგანზომილებო ფარდობით \(\frac{\Delta x}{l}\), ხოლო დაძაბულობა- ფარდობით \(\frac{F}{S}\) (ზედაპირის ერთეულზე მომქმედი ძალა). მცირე დეფორმაციებისათვის
\(\frac{\Delta x}{l}=\frac{1}{G}\frac{F}{S}.\)
ამ თანფარდობაში პროპორციულობის \(G\) კოეფიციენტს წანაცვლების მოდულს უწოდებენ. წანაცვლების მოდული მყარი მასალის უმრავლესობისათვის 2-3-ჯერ ნაკლებია იუნგის მოდულზე. მაგალითად, სპილენძისათვის E = 1,1·1011 ნ/მ2, G = 0,42·1011 ნ/მ2. უნდა გვახსოვდეს, რომ თხევადი და აირადი ნივთიერებისთვის წანაცვლების მოდული ნულის ტოლია.
ნახ. 1.(3)-ზე სითხეში ჩაძირული სხეულის ყოველმხრივი შეკუმშვის დეფორმაციაა მოცემული. ამ შემთხვევაში მექანიკური დაძაბულობა სითხეში p წნევის ტოლია. ფარდობითი დეფორმაცია განისაზღვრება როგორც მოცულობის \(\Delta V\) ცვლილების ფარდობა საწყის მოცულობასთან. მცირე დეფორმაციებისას
\(\frac{\Delta V}{V}=\frac{1}{B}p.\)
ამ ფორმულაში პროპორციულობის კოეფიციენტს ყოველმხრივი შეკუმშვის მოდულს უწოდებენ.
ყოველმხრივი შეკუმშვა შეიძლება განიცადოს არა მხოლოს მყარმა სხეულმა, არამედ სითხეებმა და აირებმაც. წყლისთვის B = 2,2·109 ნ/მ2, ფოლადისთვის B = 1,6·1011 ნ/მ2. წყნარი ოკიანის ფსკერზე, დაახლოებით 4 კმ სიღრმის დონეზე, წნევა დაახლოებით 4·107 ნ/მ2.
ამ პირობებში წყლის მოცულობის ფარდობითი ცვლილება \(\frac{\Delta V}{V}\) 1,8 % შეადგენს, მაშინ როცა ფოლადის სხეულისათვის იგი მხოლოდ 0,025 %-ია, ე.ი. 70-ჯერ ნაკლები. მყარი სხეულები, მათი კრისტალური მესერებით, გაცილებით ნაკლებად კუმშვადია სითხეებთან შედარებით, რომელთა ატომები და მოლეკულები ნაკლებად არიან დაკავშირებული მეზობლებთან. აირების კუმშვადობა მრავალი რიგით უფრო დიდია სითხეებისა და მყარი სხეულების კუმშვადობაზე.
ყოველმხრივი შეკუმშვის მოდულის სიდიდე მოცემულ ნივთიერებაში ბგერის სიჩქარით განისაზღვრება.


