არაერთგვაროვანი უბნების შემცველი რთული ელექტრული წრედების გათვლის გასამარტივებლად გამოიყენება კირხოფის წესი, რომელიც ომის კანონის განზოგადოებაა განშტოებული წრედებისათვის.
განშტოებულ წრედებში შეიძლება გამოვყოთ საკვანძო წერტილები (კვანძები), რომლებშიც შედის არანაკლებ სამი გამტარისა (ნახ. 1). კვანძებში შემავალი დენები მიღებულია ჩაითვალოს დადებითად; კვანძიდან გამომავალი კი უარყოფითად.
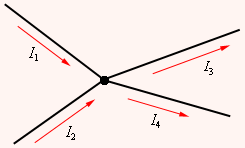
ნახ. 1.
ელექტრული წრედის კვანძი. I1, I2 > 0; I3,I4 < 0
მუდმივი დენის წრედის კვანძში არ შეიძლება ხდებოდეს მუხტის დაგროვება. აქედან გამომდინარეობს კირხოფის პირველი წესი:
განშტოებული წრედის ყოველი კვანძისათვის დენის ძალების ალგებრული ჯამი ნულის ტოლია:
I1 + I2 + I3 + ... + In = 0.
კირხოფის პირველი წესი ელექტრული მუხტის შენახვის კანონის შედეგს წარმოადგენს.
განშტოებულ წრედში შეიძლება გამოიყოს ერთგვაროვანი და არაერთგვაროვანი უბნებისაგან შედგენილი ჩაკეტილი გზების გარკვეული რაოდენობა. ასეთ ჩაკეტილ გზებს კონტურებს უწოდებენ. გამოყოფილი კონტურის სხვადასხვა უბანში შეიძლება გადიოდეს სხვადსხვა დენი. ნახ. 2-ზე უბრალო განშტოებული წრედის მაგალითია წარმოდგენილი. წრედი ორ a და d კვანძს შეიცავს, რომლებშიც ერთნაირი დენი შედის; ამიტომ მათგან მხოლოდ ერთი არის დამოუკიდებელი (a ან d).
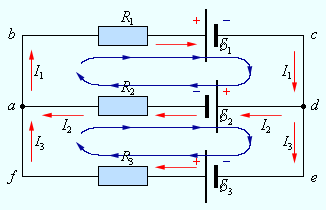
ნახ. 2.
უბრალო განშტოებული წრედის მაგალითი. წრედი ერთ დამოუკიდებელ კვანძს (a ან d) და ორ დამოუკიდებელ კონტურს შეიცავს (მაგალითად,abcd და adef)
წრედში შეიძლება გამოიყოს სამი კონტური abcd, adef და abcdef. მათგან მხოლოდ ორია დამოუკიდებელი (მაგალითად,, abcd და adef), რადგანაც მესამე არ შეიცავს არანაირ ახალ უბანს.
კიტხოფის მეორე წესი ომის განზოგადოებული კანონის შედეგს წარმოსდგენს.
ჩავწეროთ ომის განზოგადოებული კანონი 2-ზე წარმოდგენილი წრედის ერთ-ერთი კონტურის შემადგენელი უბნისთვის, მაგალითად, abcd-სათვის. ამისათვის ყოველი უბნისთვის უნდა მივუთითოთ დენის დადებითი მიმართულება და კონტურის შემოვლის დადებითი მიმართულება. ომის განზოგადოებული კანონის ჩაწერისას ყოველი უბნისთვის აუცილებელია დაცული იქნეს გარკვეული „აღნიშვნების წესი“,რომელიც ნახ. 3-ზე არის განმარტებული.
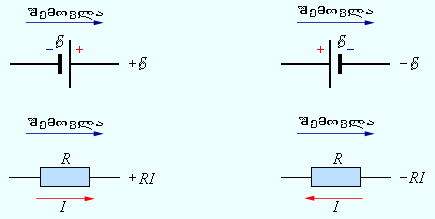
ნახ. 3.
„აღნიშნების წესი“
abcd კონტურისთვის ომის განზოგადოებული კანონი ჩაიწერება შემდეგი სახით:
bc უბნისათბის: I1R1 = Δφbc –  1.
1.
da უბნისათბის: I2R2 = Δφda –  2.
2.
თუ ამ ტოლობების მარჯვენა და მარცხენა მხარეების შევკრებთ და გავითვალისწინებთ, რომ Δφbc = – Δφda , მივიღებთ:
I1R1 + I2R2 = Δφbc + Δφda –  1 +
1 +  2 = –
2 = – 1 –
1 –  2.
2.
ანალოგიურად, adef კონტურისათვის შეიძლება ჩაიწეროს:
– I2R2 + I3R3 =  2 +
2 +  3.
3.
კირხოფის მეორე წესი შეიძლება ასე ჩამოვაყალიბოთ: მუდმივი დენის ნებისმიერი განშტოებული წრედის ყოველი ჩაკეტილი კონტურის წინაღობის ამ უბნის დენის ძალაზე ნამრავლების ალგებრული ჯამი ტოლია ამ კონტურის გასწვრის ემძ-ს ალგებრული ჯამისა.
განშტოებული წრედის ყველა დამოუკიდებელი კვანძებისა და კონტურებისთვის ჩაწერილი კირხოფის პირველი და მეორე წესების ერთობლიობა იძლევა ელექტრული წრედისთვის ძაბვებისა და დენის ძალების გათვლისთვის აუცილებელ და საკმარის ალგებრულ განტოლებათა რაოდენობას. ნახ. 2-ზე მოცემული წრედისათვის, სამი უცნობი I1, I2 და I3 დენის ძალის განსაზღვრისათვის განტოლებათა სისტემას აქვს სახე:
I1R1 + I2R2 = –  1 –
1 –  2,
2,
– I2R2 + I3R3 =  2 +
2 +  3,
3,
– I1 + I2 + I3 = 0.
ამგვარდ, კირხოფის წესს განშტოებული წრედის გათვლები დაჰყავს წრფივი ალგებრული სისტემის ამიხსნამდე. ამ განტოლებათა სისტემის ამოხსნა რაიმე პრიციპულ სირთულეს არ წარმოადგენს, მაგრამ ხანდახან ძალიან გრძელია უბრალო წრედების შემთხვევაშიც. თუ ამოხსნის შედეგად რომელიმე უბანზე დენის ძალა უარყოფითი აღმოჩნდება, ეს იმაზე მიუთითებს, რომ დენი ამ უბანზე მოძრაობს აღებული დადებითი მიმართულიბის საწინააღმგეგოდ.


