უმარტივეს მოწყობილობას, რომელსაც საგნის გამოსახულების შემქმნა შეუძლია, ბრტყელი სარკე ეწოდება. ბრტყელი სარკოთ შქმნილი საგნის გამოსახულება სარკის ზედაპირიდან არეკვლილი სხივების საშუალებით იქმნება. ეს გამოსახულება წარმოსახვითია, რადგან ის იქმნება არა თვითონ არეკვლილი სხივების, არამედ მათი გაგრძელებების სარკის მიღმა გადაკვეთით (ნახ. 1).
ნახ. 1.
სარკიდან არეკვლილი სხივების სვლა. S' წერტილი S წერტილის წარმოსახვითი გამოსახულებაა.
სინათლის არეკვლის კანონის შედეგად საგნის წარმოსახვითი გამოსახულება სარკის ზედაპირის მიმართ სიმეტრიულად თავსდება. გამოსახულების ზომა საგნის ზომის ტოლია.
სფერულ სარკეს უწოდებენ ამრეკვლ ზედაპირს, რომელსაც სფერული სეგმენტის სახე აქვს. იმ სფეროს ცენტრს, რომლისაგანაცაა ეს სეგმენტი მოჭრილი სარკის ოპტიკურ ცენტრს უწოდებენ. სფერული სეგმენტის წვეროს პოლუსს უწოდებენ. ოპტიკურ ცენტრსა და პოლუსზე გამავალ სწორს სფერული სარკის მთავარ ოპტიკურ ღერძს უწოდებენ. მთავარი ოპტიკური ღერძი მხოლოდ იმით განსხვავდება ოპტიკურ ცენტრზე გამავალი ყველა სხვა ღერძისაგან, რომ ის სარკის სიმეტრიის ღერძს წარმოადგენს.
სფერული სარკე შეიძლება იყოს ჩაზნექილი და ამოზნექილი. თუ ჩაზნექილ სფერულ სარკეს მთავარი ოპტიკური ღერძის მთავარი ოპტიკური ღერძის პარალელური სხივთა კონა ეცემა, მაშინ სარკიდან არეკვლის შემდეგ სხივები გადაიკვეთებიან წერტილში, რომელსაც სარკის მთავარი ფოკუსი F ეწოდება. ფოკუსიდან სარკის პოლუსამდე მანძილს ფოკუსურ მანძილს უწოდებენ და აღნინავენ F ასოთი. ჩაზნექილი სფერული სარკის მთავარი ფოკუსი ნამდვილია. ის სარკის ცენტრსა და პოლუსს შორის მანძილის შუაში მდებარეობს (ნახ. 2).
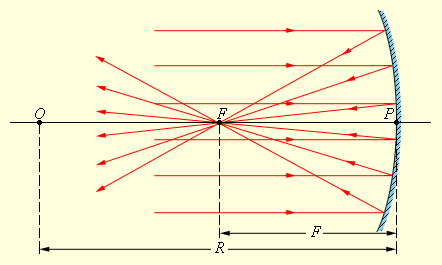
ნახ. 2.
ჩაზნექილი სარკის ზედაპირიბად სხივების პარალელური კონის არეკვლა. O წერტილი ოპტიკური ცენტრია, P - პოლუსი, F - სარკის მთავარი ფოკუსი; OP - მთავარი ოპტიკური ღერძი, R - სარკის სიმრუდის რადიუსი
მხედველობაში უნდა ვიქონიოთ, რომ არეკვლილი სხივები იკვეთება დაახლოებით ერთ წერტილში მხოლოდ იმ შემთხვევაში, თუ დაცემული პარალელური კონა საკმარისად ვიწროა (ე.წ. პარაქსიალური კონა).
ამოზნექილი სარკის მთავარი ფოკუსი წარმოსახვითია. თუ ამოზნექილი სარკეზე მთავარი ოპტიკური ღერძის პარალელური სხივთა კონა ეცემა, მაშინ არეკვლის შემდეგ ფოკუსში გადაიკვეთება არა თვით სხივები, არამედ მათი გაგრძელებები (ნახ. 3).
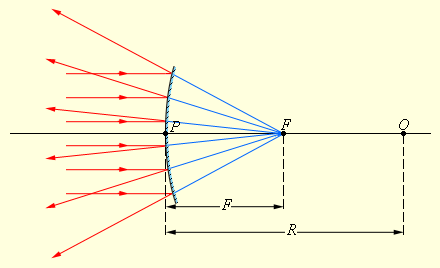
ნახ. 3.
ამოზნექილი სარკის ზედაპირიდან სხივების პარალელური კონის არეკვლა. O ოპტიკური ცენტრია, P - პოლუსი, F - სარკის წარმოსახვითი ფოკუსი, OP - მთავარი ოპტიკური ღერძი
სფერული სარკის ფოკუსური მანძილი გარკვეული ნიშანი აქვს: ჩაძნექილი სარკისათვის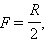 
ამოზნექილისათვის 
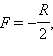სადაც R – სარკის სიმრუდის რადიუსია.
სფერულ სარკეში რაიმე A წერტილი გამოსახულება შეიძლება სტანდარტული სხივების ნებისმიერი წყვილის საშუალებით:
- სარკის ოპტუკურ ცენტრზე გამავალი AOC სხივი; არეკვლილი COA სხივი მიჰყვება იგივე სწორს;
- სარკის ფოკუსში გამავალი AFD სხივი; არეკვლილი სხივი მთავარი ოპტიკური ღერძის პარალელურად გადის;
- სარკის პოლუსზე დაცემული AP სხივი; არეკვლილი სხივი დაცემულის სიმეტრიულია მთავარი ოპტიკური ღერძის მიმართ.
- მთავარი ოპტიკური ღერძის პარალელური AE სხივი; არეკვლილი EFA1 სხივი სარკის ფოკუსზე გადის.
ნახ. 4-ზე ზემოთ ჩამოთვლილი სტანდარტული სხივები ჩაზნექილი სარკის მაგალითზეა ნაჩვენები. ყველა სხივი გადის A' წერტილზე, რომელიც A წერტილის გამოსახულებას წარმოადგენს. ყველა სხვა არეკვლილი სხივები ასევე A' წერტილში გადის. სხივთა სვლას, რომლის დროსაც ერთი წერტილიდან გამოსული ყველა სხივი მეორე წერტილში იკრიბება, სტიგმატურს უწოდებენ. A'B' მონაკვეთი AB სხეულის გამოსახულებაა. აგება ამოზნექილი სარკისათვისაც ანალოგიურია.
ნახ. 4.
გამოსახულების აგება ჩაზნექილ სფერულ სარკეში
გამოსახულების მდებარეობა და ზომა შეიძლება განისაზღვროს სფერული სარკის ფორმულისათვის:
სადაც d – სხეულიდან სარკემდე მანძილი, f – სარკიდან გამოსახულებამდე მანძილი. d და f სიდიდეები ნიშნების გარკვეულ წესს ემორჩილება:
- d > 0 და f > 0 – ნამდვილი საგნებისა და გამოსახულებებისთვის;
- d < 0 და f < 0 – წერმოსახვითი საგნებისა და გამოსახულებებისთვის.
ნახ. 4-ზე გამოსახული შემთხვევისათვის გავაქვს:
F > 0 (ჩაზნექილი სარკე); d = 3F > 0 (ნამდვილი საგანი).
სფერული სარკის ფორმულით ვღებულობთ: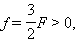 
, აქედან გამომდინარე, გამოსახულება ნამდვილია.
ჩაზნექილი სარკის ადგილას, სიდიდით ისეთივე ფოკუსური მანძილის მქონე, ამოზნექილი სარკე რომ იყოს ჩვენ მივიღებთ შემდეგ შედეგს:
F < 0, d = –3F > 0,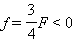 
– წარმოსახვითი გამოსახულება.
სფერული სარკის წრფივი გადიდება Γ განისაზღვრება როგორც გამოსახულების h' და საგანის h სიდიდეების ფარდობისა.
h' სიდიდეს მოსახერხებელია მივუწეროთ გარკვეული ნიშანი იმის მიხედვით, გამოსახულება პირდაპირია (h' > 0) თუ გადაბრუნებული (h' < 0). h სიდიდე ყოველთვის დადებით სიდიდეთ ითვლება. ასეთი განსაზრვრის დროს სფერული სარკის წრფივი გადიდება გამოისახება ფორმულით; რომელიც ნახ. 4-დან ადვილად მიიღება:
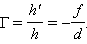
ზემოთ განხილულ პირველ მაგალითში 
– გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული. მეორე მაგალითში 
– გამოსახულება პირდაპირია და ოთხჯერ შემცირებული.