ნებისმიერი ფიზიკური გაზომვის შესრულებისას უმნიშვნელოვანეს როლს ხდომილებებს შორის სივრცე-დროითი თანაფარდობა ასრულებს. ფარდობითობის სპეციალურ თეორიაში ხდომილება განისაზღვრება როგორც ფიზიკური მოვლევა, რომელიც არჩეულ ათვლის სისტემაში სივრცის რაიმე წერტილში დროის რაღაც მომენტში ხდება. ამგვარად, ხდომილება რომ ბოლომდე დახასიათდეს, საჭიროა არა მარტო მისი ფიზიკური შინაარსის გამოკვლევა, არამედ მისი ადგილისა და დროის განსაზღვრა. ამისათვის აუცილებელია მანძილისა და დროის შუალედების გაზომვის პროცედურების გამოყენება. აინშტაინმა აჩვენა, რომ ეს პროცედურები მკაცრ გასაზღვრას საჭიროებან.
იმისთვის, რომ არჩეულ ათვლით სისტემაში სივრცის ერთსადაიმავე წერილში მიმდინარე ორ ხდომილებას შორის (მაგალითად რაიმე პროცესის დასაწყისსა და დასასრულს შორის) დროის შუალედის გაზომვა შესრულდეს, საკმარისია ეტალონური საათის ქონა. დღეისთვის ყველაზე დიდ სიზუსტით ამიაკის მოლეკულების (მოლეკულური საათი) ან ცეზიუმის ატომების (ატომური საათი) საკუთარ რხევებზე დაფუძვნებული საათები გამოირჩევიან. დროის შუალედების გაზომვა ემყარება ერთდროულობის ცნებას: რაიმე პროცესის ხანგრძლივობა იმ დროის შუალედთან შედარებით განისაზღვრება, რომელიც საათის პროცესის დაწყების ერთდროულ ჩვენებასა და იგივე საათის პროცესის დასრულების ერთდროულ ჩვენებას აშორებს ერთმანეთისაგან. თუ ორივე ხდომილება სხვადასხვა ათვლის სისტემაში ხდება, მათ შორის დროის შუალედის გაზომვისთვის ამ წერტილებში უნდა იყოს სინქრონიზებული საათები.
საათების სინქრონიზაციის პროცესის აინშტაინისეული განმარტება დამყარებულია იმაზე, რომ ვაკუუმში სინათლის სიჩქარე დამოკიდებული არ არის გავრცელების მიმართულებაძე. ვთქვათ A წერტილიდან A-ს საათის მიხედვით დროის t1 მომენტში გამოდის სინათლის მოკლე იმპულსი (ნახ. 1). ვთქვათ B წერტილში მოსვლის და უკან არეკვლის დრო B -ს საათზე ტოლია t'. და ბოლოს, ვთქვათ არეკვლილი სიგნალი A -ში ბრუდება A-ს საათის მიხედვით დროის t2 მომენტში. მაშინ, განმარტების მიხედვით A და B-ში საათები სინქრონული იქნება, თუ t' = (t1 + t2) / 2.
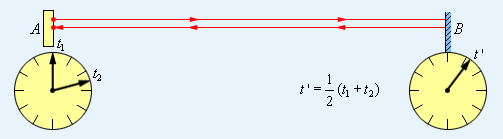
ნახ. 1.
საათების სინქრონიზაცია ფარდობითობის სპეციალური თეორიის მიხედვით
ათვლის სისტემის არჩევისგან დამოუკიდებელი ერთიანი მსოფლიო დროის არსებობა, რაც უცილობელ ფაქტად ითვლებოდა კლასიკურ ფიზიკაში, უსასრულოდ დიდი სიჩქარით მოძრავი სიგნალის საშუალებით საათების სინქრონიზაციის არაპირდაპირი დაშვების ექვივალენტურია.
ამგვარდ, არჩეული ათვლის სისტემის სხვადასხვა წერტილებში სინქრონული საათების განლაგება შეიძლება. ახლა შესაძლებელია სივრცულად განსხვავებელ წერტილებში მიმდინარე ხდომილებათა ერთდროილობის ცნების განმარტება: ეს ხდომილებები ერთდროულია, თუ სინქრონიზირებული საათები ერთსადაიმავე დროს აჩვენებენ.
ახლა განვიხილოთ მეორე ინერციული K' სისტემა , რომელიც K სისტემის x ღერძის დადებითი მიმართულებით რაღაც υ სიჩქარით მოძრაობს. ამ ახალი ათვლის სისტემის სხვადასხვა წერტილებში ასევე შეაძლებელია საათების განლაგება და მათი ზემოთ აღწერილი პროცედურის მიხედვით სინქრონიზაცია. ახლა უკვე ორ ხდომილებას შორის დროის ინტერვალი შეიძლება გაიზომოს როგორც K სისტემის, ასევა K' სისტემის საათებით. იქნებიან თუ არა ეს ინტერვალები ერთნაერი? ამ კითხვაზე პასუხი ფარდობითობის სპეციალური თეორიის პოსტულატებთან თანხმობაში უნდა იყოს.
ვთქვათ ორივ ხდომილება K' სისტემაში ერთსადაიმავე წერტილში ხდება და მათ შორის დროის შუალედი K' სისტემის საათით τ0 ტოლია. დროის ამ შუალედს საკუთარ დროს უწოდებენ. როგორი იქნება დროის შუალედი იგივე ხდომილებებს შორის, თუ მას K სისტემის საათით გავზომავთ?
ამ კითხვაზე პასუხის გასაცემად განვიხილოდ შემდეგი აზრობრივი ექსპერიმენტი. რაღაც l სიგრძის მყარი ძელაკის ერთ-ერთ ბოლოზე მიმაგრებულია იმპულსური ნათურა B, ხოლო მეორე ბოლოზე - ამრეკლი სარკე M. ძელაკი K' სისტემაში მოთავსებულია უძრავად და y' ღერძის პარალელურადაა ორიენტირებული (ნახ. 2). ხდომილება 1 – ნათურის ანთება, ხდომილება 2 – მოკლე სინათლის იმპულსის ნათურასთან დაბრუნება.
ნახ. 2.
დროის შუალედების ფარდობითობა. K' სისტემაში ხდომილებების დადგომის მომენტი ერთიდაიგიცე C საათით ფიქსირდება, K სისტემაში კი - ორი სინქრონიზებული სივრცილად დაშორებული C1 და C2 საათით. K' სისტემა მოძრაობს υ სიჩქარით K სისტემის x ღერძის დადებითი მიმართულებით
K' სისტემაში ორივე განსახილველი ხდომილება ერთსადაიმავე წერტილში ხდება. მათ შორის დროის შუალედი (საკუთარი დრო) ტოლია τ = 2l /. K სისტემაში მყოფი დამკვირვებლისთვის სინათლის იმპულსი სარკეებს შორის მოძრაობს ზიგზაგისებურად და გადის 2L მანძილს, რომელიც ტოლია
სადაც τ – K სისტემაში ბდებარე C1 და C2 სინქრონული საათებით გაზომილი სინათლის იმპულსის გამოსვლასა და დაბრუნებას შორის დროის შუალედია. მაგრამ, ფარდობითობის სპეციალური თეორიის მეორე პოსტულატის მიხედვით K სისტემაში სინათლის იმპულსი იგივე c სიჩქარით მოძრაობდა, როგორითაც K' სისტემაში. აქედან გამომდინარე, τ = 2L / c.
ამ თანაფარდობებიდან შეიძლება τ-სა და τ0-ს შორის დამოკიდებულების პოვნა:
სადაც β = υ / c.
ამგვარად, ორ ხდომილებას შორის დროის შუალედი ათვლის სისტემაზეა დამოკიდებული, ე.ი. ფარდობითია. საკუთარი დრო ყოველთვის ნაკლებია, ვიდრე ნებისმიერ სხვა ათვლით სისტემაში გაზომილი ამ ხდომილებათა შორის დროის შუალედი. ამ ფაქტს რელატივისტურად შენელებული დრო ეწოდება. დროის შენელება სინათლის სიჩქარის ინვარიანტულობის შედეგია.
დროის შენელების ეფექტი K და K' ინერციული სისტემების თანაბარუფლებიანიბის პოსტულატიდან გამომდინარე ურთიერთშექცევადია: ნებისმიერი დამკვირვებლისათვის K ან K' -ში დამკვირვებლის მიმართ მოძრავ სისტემასთან დაკავშირებული საათი უფრო ნელა მიდის (მუშაობს). ეს დასკვნა ფარდობითობის სპეციალური თეორიის პირდაპირი ცდისეული დადასტურებაა. მაგალითად, კოსმოსური სხივების შესწავლისას მათ შემადგენლობაში აღმოჩნდა μ-მეზონები - ელემენტარული ნაწილაკები, რომელთა მასა დაახლოებით 200-ჯერ აჭარბებს ელექტრონის მასას. ეს ნაწილაკები სტაბილურები არ არიან, მათი სიცოცხლის საშუალო საკუთარი დრო ტოლია τ0 = 2,2·10–6 წმ. მაგრამ კოსმოსურ სხივებში μ-მეზონები მოძრაობენ სინათლის სიჩქარის მახლობელი სიჩქარით. დროის შენელების რელატივისტური ეფექტის გათვალისწინების გარეშე ისინი ატმოსფეროში გაიფრენდნენ cτ0 ≈ 660 მ ტოლ მანძილს. სინამდვილეში, როგორც გამოცდილება უჩვენებს, მეზონები სიცოცხლის დროის განმავლობაში დაშლის გარეშე გაცილებით დიდ მანძილის გავლას ასწრებენ. ფარდობითობის სპეციალური თეორიის მიხედვით, მეზონის სიცოცხლის საშუალო დრო დედამიჭაზე მყოფი დამკვირვებლის საათის მიხედვით ტოლია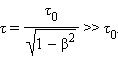 
, რადგანაც β = υ / c ერთთან ახლოა. ამიტომ დედემიწასთან დაკავშირებულ ათვლის სისტემაში მეზონის მიერ გავლილი საშუალო მანძილი υτ 660 მ-ზე გაცილებით მეტი აღმოჩნდება.
დროის შენელების რელატივისტურ ეფექტთან დაკავშირებულია ე.წ. „ტყუპების პარადოქსი“. იგულისმება, რომ ერთ-ერთი ტყუპისცალი დარჩა დედამიწაზე და მეორე მიემგზავრება ხანგრძლივ კოსმოსურ მოგზაურობაში სუბსინათლის სიჩქარით. დედამიწაზე მყოფი დამკვირვებლისათვის კოსმოსურ ხომალდში დრო უფრო ნელა მიდის, და როცა ასტრონავტი დედამიწაზე ბრუნდება, ის თავის დედამიწაზე დარჩენილ ტყუპისცალ ძმაზე გაცილებით ახალგაზრდა იქნება. პარადოქსი იმაში მდგომარეობს, რომ იგივე დასკვნა შეუძლია გააკეთოს მეორე, მოგზაურობაში წასულ ტყუპიაცალსაც. მისთვის დრო დედამიწაზე მიდის უფრო ნელა, და შეუძლია ელოდოს, რომ ანგრძლივი მოგზაურობიდან დაბრუნებულს დედამიწაზე დარჩენილი ძმა მასთან შედარებით გაცილებით ახალგაზრდა დახვდება.
„ტყუპების პარადოქსის“ გადასჭრელად მხედველობაში უნდა იქნეს მიღებული იმ ათვლის სისტემების არათანაბარუფლებიანობა, რომლებშიც ძმები იმყოფებიან. პირველი მათგანი, დედამიწაზე დარჩენილი, მთელი ამ დროის განმავლობაში ინერციულ სისტემაში იმყოფებოდა, მაშინ როცა კოსმოსურ ხომალდთან დაკავშირებული ათვლის ისიტემა პრინციპულად არაინერციულია. კოსმოსური ხომალდი განიცდის აჩქარებას სტარტის აღების, ტრაექტორიის შორეულ წერტილში მოძრაობის მიმართულების შეცვლის და დედამიწაზე დაჯდომის მომენტში. ამიტომ, ასტრონავტი ძმის დასკვნა სწორი არ არის. ფარდობითობის სპეციალური თეორია წინასწარმეტყველებს, რომ ის მართლაც დედამიწაზე დარჩენიზე ახალგაზრდა იქნება.
თუ კოსმოსური ხომალდის სიჩქარე სინათლის c სიჩქარეზე გაცილებით ნაკლებია, დროის შენელების ეფექტი იმდენად უმნიშვნელოა, რომ შესაძლებელია მისი უგულვებეყოფა. მიუხედავად ამისა, ამ ეფექტის პირდაპირი დასაბუთაბა გახდა შესაძლებელი მაკროსკოპული საათების ექსპერიმენტის საშუალებით. ყველაზე უფრო ზუსტი საათი ცეზიუმის ატომების ნაკადზე მომუშავე ატომური საათია. ეს საათი წამში 9192631770-ჯერ „წიკწიკებს“. 1971 წელს ამერილელმა ფიზიკოსებმა შეადარეს ორი ასეთი საათი, ისე რომ ერთი ჩვეულიბრივი რეაქტიული თვითმფრინავით დედამიწის გარშემო დაფრინავდა, მეორე კი დედამიწაზე, აშშ-ს სამხედრო-საზღვაო ობსერვატორიაში იმყოფებოდა. ფარდობითობის სპეციალური თეორის თანახმად, მოგზაურობაში მყოფი საათი დედამიწაზე მყოფს (184 ± 23)·10–9 წმ-ით უნდა ჩამორჩენოდა. დაკვირვებულმა ჩამორჩენამ (203 ± 10)·10–9 წმ შეადგინა, ე.ი. დაკვირვების ცდომილების ფარგლებში. რამოდენიმე წლის შემდეგ ექსპერიმენტი გაიმეორეს დამიიღეს ფარდობითობის სპეციალური თეორიასთან 1%-იანი თანხმობა.
დღეისათვის უკვე აუცილებელია, ატომური საათების შორ მანძილზე ტრანსპორტირების შემთხვევაში, საათის შენელების რელატივისტური ეფექტის მხედველობაში მიღება