აინშტაინის ფარდობითობის პრინციპი ბუნების ყველა კანონის ინვარიანტობას ამტკიცებს ერთი ათვის ინერციული სისტემიდან მეორეში გადასვლის შემთხვევაში. ეს ნიშნავს, რომ ყველა განტოლება, რომლებიც ბუნების კანონებს აღწერენ, ინვარიანტული უნდა ივნენ ლორენცის გარდაქმნების მიბართ. ფარდობითობის სპეციალური თეორიის შექმნის მომენტისათვის ამ პირობებს, უკვე არსებული, მაქსველის ელექტროდინამიკა აკმაყოფილებდა. მაგრამ, ნიუტონის კლასიკური მექანიკის კანონები ლორენცის გარდაქმნებისადმი ინვარიანტული არ აღმოჩნდნენ, და ამიტომ ფარდობითობის სპეციალურმა თეორიამ მექანიკის კანონების გადახედვა და დაზუსტება მოითხოვა.
ასეთი გადახედვის საფუძველში აინშტაინმა ჩაკეტილ სისტემაში იმპულსისა და ენერგიის შენახვის კანონების შესრულების პირობა ჩადო. იმისათვიsს, რომ იმპულსის შენახვის კანონი ყველა ინერციულ ათვლის სისტემაში სრულდებიდეს, აუცილებელი გახდა სხეულის იმპულსის განმარტების შეცვლა. კლასიკური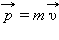 
-ს ნაცვლად ფარდობითობის სპეციალურ თეორიაში 
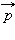სიჩქარით მოძრავი m მასის სხეულის რელატივისრური იმპულსი 
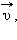ჩაიწერება შემდეგი სახით:
(*)
თუ ასეთ განმარტებას მივიღებთ, მაშინ ურთიერთმოქმედი ნაწილაკების ჯამური იმპულსის შენახვის კანონი (მაგალითად, დაჯახებებისას) ლორენცის გარდაქმნებთან დაკავშირებულ ყველა ინერციულ სისტემაში შესრულდება. როცა β → 0 რელატივისტური იმპულსი კლასიკურში გადადის. იმპულსის გამოსახულებაში შემავალი m მასა ნაწილაკის ფუნდამენტური მახასიათებელია და არ არის დამოკიდებული ათვლის ინერციული სისტემის არჩევაზე, და ე.ი. მისი მოძრაობის სიჩქარეზე. (გასული წლების ბევრ სახელმძღვანელიში მას m0 ასოთი აღნიშნავდნენ და უძრაობის მასას უწოდებდნენ. გარდა ამისა, შემოჰქონდათ ე.წ. რელატივისტური მასა, რომელიც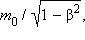 
ტოლია, და დამოკიდებულია სხეულის მოძრაობის სიჩქარეზე. თანამედროვე ფიზიკა თანდათანობით უარს ამბობს ამ ტერმინოლოგიაზე).
მატერიალური წერტილის რელატივისტური დინამიკის ძირითადი კანონი ისევე ჩაიწერება, როგორც ნიუტონის მეორე კანონი:
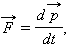
მხოლოდ ფარდობითობის სპეციალურ თეორიაში 
-ში ნაწილაკის რელატივისტური იმპულსი იგულისხმება. აქედან გამომდინარე,
რადგანაც რელატივისტური იმპულსი ნაწილაკის სიჩქარის პროპორციული არ არის, მისი ცვლილების სიჩქარე აჩქარების პირდაპირპროპორციული არ იქნება. ამიტომ სიდიდითა და მიმართულებით მუდმივი ძალა არ იწვევს თანაბარაჩქარებულ მოძრაობას.
მაგალითად, ღერძის გასწვრის ერთგანზომილებიანი მოძრაობის დროს ან წილაკის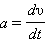 
აჩქარება მუმივი ძალის მოქმედებით ტოლი აღმოჩნდება
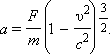
თუ კლასიკური ნაწილაკის სიჩქარე მუდმივი ძალის მოქმედებით უსაზღვროდ იზრდება, რელატივისტური ნაწილაკის სიჩქარეს არ შეუძლია გადააჭარბოს ვაკუუმში სინათლის სიჩქარეს. რელატივისტურ მექანიკაში, ნიუტონის მექანიკის მსგავსად, სრულდება ენერგიის შენახვის კანონი. სხეულის კინეტიკური ენერგია სხეულისათვის გარკვეული სიჩქარის მინიჭებისათვის საჭირო გარე ძალის მუშაობით განისაზღვრება. m მასის ნაწილაკი რომ ააჩქარო უძრაობის მდგომარეობიდან υ0 სიჩქარემდე მუდმივი F ძალის მოქმედებით, ამ ძალამ უნდა შეასრულოს მუშაობა
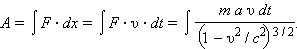
რადგანაც a dt = dυ, საბოლოოდ შეიძლება დაიწეროს
ამ ინტეგრალის გამოთვლას კინეტიკური ენერგიისათვის შემდეგ გამოსახულებამდე მივყავართ (ინდექსი „ნული“ სიჩქარის შემთხვევაში გამოტოვებულია):
აინშტაინი ამ გამოსახულების მარჯვენა ნაწილის პირველ წევრს ნაწილაკის მოძრაობის ნულოვანი ენერგიის E ინტერპრეტაციას აძლევდა, ხოლო მეორეს უძრაობის ენერგიისას E0:
(**)
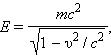E0 = mc2. (***)
რელატივისტური დინამიკის კინეტიკური ენერგია Ek სხეულის სრული ენერგიისა E და მისი უძრაობის ენერგიის E0 სხვაობას წარმოადგენს:
Ek = E – E0.
ნახ. 1-ზე კლასიკურ და რელატივისტურ კანონებზე დამოკიდებული ნაწილაკის კინეტიკური ენერგიის ცვლილებაა ნაჩვენები.
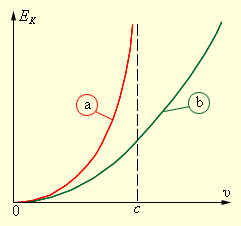
ნახ. 1.
კინეტიკური ენერგიის სიჩქარეზე დამოკიდებულება რელატივისტური (a) და კლასიკური (b) ნაწილაკისათვის. როცა υ << c კანონები ერთმანეთს ემთხვევა
რელატივისტური მექანიკის განსაკუთრებით მნიშვნელოვანია დასკვნა იმის შესახებ, რომ უძრაობის მდგომარეობაში მყოფი m მასა ენერგიის უზარმაზარ მარაგს შეიცავს. ამ მტკიცებულებას სხვადასხვაგვარი პრაქტიკული გამოყენება აქვს, ბირთვული ენერგიის გამოყენების ჩათვლით. თუ ნაწილაკის ან ნაწილაკთა სისიტემის მასა Δm -ით მცირდება, მაშინ ამ დროს უნდა გამოიყოფოდეს ენერგია ΔE = Δm · c2. მრავალრიცხოვანი პირდაპირი ექსპერიმენტები უძრაობის ენერგიის არსებობის დამაჯერებელ დასაბუთებას იძლევიან. აინშტაინის, მასასა და ენერგიის დამაკავშირებელი, ფორმულის პირველი ექსპერიმენტული დასაბუთება მიღებილი იყო რადიოაქტიური დაშლისას განთავისუფლებული ენერგიის შედარებით საწყისი ბირთვისა და ნარჩენების მასათა სხვაობასთან. მაგალითად, როცა თავისუფალი ნეიტრონის ბეტა-დაშლისას წარმოიქმნება პროტონი, ელექტრონი და კიდევ ერთი ნულოვანი მასის მქონე ნაწილაკი - ანტინეიტრინო:
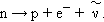
ამ დროს საბოლოო პროდუქტების ჯამური კინეტიკური ენერგია 1,25·10–13 ჯ-ს ტოლია. ნეიტრონის მასა აჭარბებს პროტონისა და ელექტრონის ჯამურ მასას Δm = 13,9·10–31 კგ-ით. მასის ასეთ შემცირებას უნდა შეესაბამებოდეს ენერგია ΔE = Δm · c2 = 1,25·10–13 ჯ, რომელიც დაშლის პროდუქტების დაკვირვებული კინეტიკურუ ენერგიის ტოლია.
რომ შეიქმნას ამ მოვლენის მასშტაბების შეგრძნება მაკროსამყაროში, ასეთი მაგალითი განვიხილოთ. 1 ტ ტრინიტროტოლუოლის აფეთქებისას თავისუფლდება 4,2·109 ჯ ენერგია. მეგატონიანი ბომბის აფეთქებისას გამოიყოფა 4,2·1015 კ ენერგია. ამ უზარმაზარი ენერგიის შესაბამისი მასა m = E / c2 მხოლოდ 46 გრამის ტოლია. ამგვარად, მეგატონიანი ბირთვული ბომბის აფეთქებისას ატომურმა „ასაფეთქებელმა“ უნდა მოიკლოს დაახლოებით 50გ-ით. წყალბადის ბომბის სრული საწყისი მასის ექვივალენტი სიმძლავრის მიხედვით 1 მეგატონიანი ტრინიტროლუოლი, დაახლოებით 1000-ჯერ მეტია და 50 კგ-ს შეადგენს.
მასისა და ენერგიის პროპორციულობის კანონი ფარდობითობის სპეციალური თეორიის ერთ-ერთ ყველაზე მნიშვნელოვან დასკვნას წარმოადგენს. მასა და ენერგია სხეულის განსხვავებული თვისებებია. მასა ახასიათებს მის ინერტულობასა და უნარს გრავიტაციული კავშირი დაამყაროს სხვა სხეულებთან. ენერგიის უმნიშვნელოვანეს თვისებას მისი უნარი წარმოადგენს, სხვადასხვა ფიზიკურ პროცესებში ერთი ფორმის ენერგიიდან ექვივალენტური რაოდენობით მეორე ფორმაში გადავიდეს. ამაში მდგომარეობს ენერგიის შენახვის კანონი. მასისა და ენერგიის პროპორციულობა მატერიის შინაგან ბუნებას გამოხატავს. აინშტაინის ფორმულა
E0 = mc2
ბუნების ფუნდამენტურ კანონს გამოსახავს, რომელსაც მასისა და ენერგიის ურთიერთკავშირის კანონს უწოდებენ.
რელატივისტური იმპულსის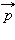 
(*) გამოსახულებისა და სრული E ენერგიის გამოსახულების (**) კომბინირებით შეიძლება მივიღოს ამ სიდიდეების დამაკავშირებელი გამოსახულებები. ამისათვის მისახერხებელია (*) და (**) ფორმულები შემდეგი სახით გადავწეროთ:
(*)
(**)
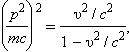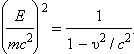გამოკლებით მივიღებთ
E2 = (mc2)2 + (pc)2.
აქედან კიდევ ერთხელ გამოდის, რომ უძრავი ნაწილაკებისათვის (p = 0) E = E0 = mc2.
მიღებული დამოკიდებულება უჩვენებს, რომ ნაწილაკს შეიძლება ჰქონდეს ენერგია და იმპულსი, მაგრამ არ ჰქონდეს მასა (m = 0). ასეთ ნაწილაკებს უმასოებს უწოდებენ. უმასო ნაწილაკებისათვის ენერგიისა და იმპულსის დამოკიდებულება უბრალო ფორმულით გამოისახება.
E = pc.
უმასო ნაწილაკებს მიეკუთვნებიან ფოტონები - ელექტრომაგნიტური გამოსხივების ქვანტები და შესაძლოა, ნეიტრინო. უმასო ნაწილაკებს უძრაობის მდგომარეობაში არსებობა არ შეუძლიათ, ყველა ათვლის ინეციულ სისტემაში ისინი ზღვრული c სიჩქარით მოძრაობენ.