გალილეის კლასიკური გარდაქმნები ფარდობითობის სპეციალურ თეორიაში არ გამოდგება, ამიტომ უნდა შეიცვალოს. ამ ახალმა გარდაქმნებმა კავშირი უნდა დაადგინოს K ათვლის სისტემაში დაკვირვებული ხდომილების დროის t მომენტსა და (x, y, z) კოორდინატებს და K' ათვლის სისტემაში დაკვირვებული იგივე ხდომილების t' დროის მომენტსა და (x', y', z') კოორდინატებს შორის.
კოორდინატებისა და დროის კინემატიკურ გარდაქმნის ფორმულებს ფარდობითობის სპეციალურ თეორიაში ლორენცის გარდაქმნებს უწოდებენ. ისინი ფარდობითობის სპეციალურ თეორიაის გამოჩენამდე 1904 წელს იყო შემოთავაზებული, როგორც გარდაქმნები რომლის მიმართაც ინვარიანტულია ელექტრომაგნიტური ფორმულები. იმ შმთხვევაში თუ K' სისტემა K სისტემის მიმართ υ სიჩქარით მოძრაობს x ღერძის მიმართ, მაშინ ლორენცის გარდაქმნებს აქვთ სახე:
K' → K K → K'
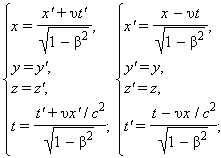
β = υ / c.
ლორენცის გარდაქმნებიდან მთელი რიგი შედეგები გამოდის. კერძოდ, მათგან გამოდის დროის შენელების რელატივისტური ეფექტი და სიგრძის ლორენცის შეკუმშვა. ვთქვათ, მაგალითად, K' სისტემის რაღაც x' წერტილში მიმდინარეობს τ0 = t'2 – t'1 (საკუთარი დრო) ხანგრძლივობის პროცესი, t'1 და t'2 – სადაც პროცესის დასაწყისისა და დასარულის შესაბამისი საათის ჩვენებებია K' სისტემაში. ამ პროცესის τ ხანგრძლივობა K სისტემაში ტოლი იქნება
ანალოგიურად, შეიძლება ვაჩვენოთ, რომ ლორენცის გარდაქმნიდან გამოდის სიგრძის შეკუმშვა. ლორენცის გარდაქმნების ერთ-ერთი უმნიშვნელოვანესი შედეგია დასკვნა ერთდროულობის ფარდობითობის შესახებ. ვთქათ, მაგალითად, ათვლის K' სისტემის ორ განსხვავებულ (x'1 ≠ x'2) წერტილში K' სისტემაში მყოფი დამკვირვებლისათვის ერთდროულად (t'1 = t'2 = t') მიმდინარეობს ორი ხდომილება. ლორენცის გარდაქმნებიდან გამომდინარე K სისტემის დამკვირვებელისთვის
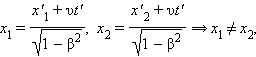
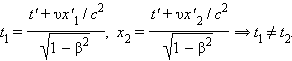
აქედან გამომდინარე, K სისტემაში ეს ხდომილებები, რჩებიან რა სივრცულად დაშორებულნი, აღარ იქნებიან ერთდროული. უფრო მეტიც, t2 – t1 სხვაობის ნიშანი υ(x'2 – x'1) გამოსახულების ნიშნით განისაზღვრება, ამიტომაც ზოგ ათვლით სისტემაში პირველი ხდომილება შეიძლება წინ უსწრებდეს მეორეს, მაშინ როცა სხვა ათვლით სისტემებში, პირიქით, მეორე ხდომილება უსწრებს პირველს. ფარდობითობის სპეციალური თეორიის ეს შედეგი არ ეხება მიზეზ-შედეგობრივი კავშირებით დაკავშირებულ ხდომილებებს, როცა ერთი ხდომილება მეორის ფიზიკურ შედეგს წარმოადგენს. შეიძლება ითქვას, რომ ფარდობითობის სპეციალური თეორია არ არღვევს მიზეზობრიობის პრინციპს და ხდომილებების მიზეზ-შედეგობრივი მონაცვლეობა ერთიდაგივეა ყველა ინერციულ ათვლის სისტემაში.
სივრცულად-გათიშული ხდომილებების ერთდროულობის ფარდობითობას შეიძლება შემდეგ მაგალითზე დავაკვირდეთ.
ვთქათ K'ათვილის სისტემის x' ღერძის გასწვრივ უძრავად გრძელი მყარი ძელაკი მდებარეობს. ძელაკის ცენტრში იმპულსური B ნათურა, ხოლო მის ბოლოებზე ორი სინქრონული საათია მოთავსებული (ნახ. 1(a)), K' სისტემა K სისტემის x ღერძის მიმართ υ სიჩქარით მოძრაობს. დროის რაღაც მომენტში ნათურა ძელაკის ბოლოებისკენ მოკლე იმპულსს აგზავნის. ორივე მიმართულების თანაბარუფლებიანობიდან გამომდინარე სინათლე K' სისტემაში ძელაკის ბოლოებამდე მივა ერთდროულად, და ძელაკის ბოლოებზე დამაგრებული საათები ერთიდაიგივე t' დროს აჩვენებენ. სისტემის მიმართ ძელაკის ბოლოები სიჩქარით მოძრაობენ ისე, რომ ერთი ბოლო მიძრაობს სინათლის იმპულსის შემხვედრი მიმაერთულებით, მეორე ბოლოს უწევს დაეწიოს სინათლეს. რადგანაც სინათლის იმპულსის გავრცელების სიჩქარე ორივე მიმართულებით ერთნაერია და ტოლია c -სი, K სისტემაში მყოფი დამკვირვებლისთვის სინათლე უფრო ჩქარა მარცხენა ბოლომდე მივა, ვიდრე მარჯვენამდე (ნახ. 1(b)).
ნახ http://suomenviagracialis.com/. 1.
ერთდროულობის ფარდობითობა. K' ათვილს სისტემაში სინათლის იმპულსი მყარი ძელაკის ბოლოებამდე ერთდროულად აღწევს (a) და სხვადასხვა დროს K ათვლის სისტემაში (b)
ლორენცის გარდაქმნები დროიში შუალედებისა და მანძილის ფარდობითობის ხასიათს გამოსახავს. მაგრამ ფარდობითობის სპეციალურ თეორიაში სივრცისა და დროის ფარდობითი ხასიათის მტკიცებულებების გვერდით მნიშვნელოვან როლს ასრულებს იმ ფიზიკური სიდიდეების ინვარიანტულობის დადგენა, რომლებიც არ იცვლებიან ერთი ათვლის სისტემიდან მეორეში გადასცლისას. ერთ-ერთ ასეთ სიდიდეს ვაკუუმში სინათლის გავრცელების სიჩქარე წარმოადგენს, რომელიც ფარდობითობის სპეციალურ თეორიაში აბსოლუტურ ხასიათს იძენს. მეორე მნიშვნელოვან ინვარიანტულ სიდიდეს, რომელიც სივრცულ-დროითი კავშირების აბსოლუტურ ხასიათს ასახავს, ხდომილებათა შორის ინტერვალია.
სივრცულ-დროითი ინტერვალი ფარდობითობის სპეციალურ თეორიაში შემდეგი თანაფარდობით განისაზღვრება:
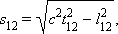
სადაც t12 – რაღაც ათვლით სისტემაში ხდომილებებს შორის დროის ინტერვალია, ხოლო l12 – იგივე სისტემაში განსაზღვრული იმ წერტილებს შორის მანძილი რომლებშიც ეს ხდომილებები ხდება. კერძო შემთხვევაში, როცა ერთ-ერთი ხდომილება ათვლის სისტემის კოორდინატთა სათავეში (x1 = y1 = z1 = 0) ხდება დროის t1 = 0 მომენტში, მეორე კი x, y, z კოორდინატების მქონე წერტილში დროის t მომენტში, ამ ხდომილებებს შორის სივრცულ-დროითი ინტერვალი ასე ჩაიწერება
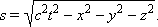
ლორენცის გარდაქმნების საშუალებით შეიძლება დამტკიცდეს, რომ ორ ხდომილებას შორის სივრცულ-დროითი ინტერვალი ერთი ინერციული ათვლის სისტემიდან მეორეზე გადასვლისას არ იცვლება. ინტერვალის ინვარიანტულობა ნიშნავს, რომ მანძილისა და დრო შუალედის ფარდობითობის მიუხედავად, ფიზიკური პროცესების მიმდინარეობას ობიექტური ხასიათი აქვს და ათვლის სისტემის არჩევაზე დამოკიდებული არ არის.
თუ ერთ-ერთ ხდომილებას კოორდინატთა სათავეში დროის t = 0 მომენტში სინათლის ხანლოკლე ანთება წარმოადგენს, ხოლო მეორეს სინათლის ფრონტის x, y, z კოორდინატების მქონე წერტილში დროის t მომენტში მოსვლა (ნახ. 3), მაშინ
x2 + y2 + z2 = c2t2,
და აქედან გამომდინარე, ინტერვალი ხდომილებათა ამ წყვილისთვის s = 0. ათვლის სხვა სისტემაში მეორე ხდომილების კოორდინატები და დრო სხვა იქნება, მაგრამ ამ სისტემაშიც სივრცულ-დროითი ინტერვალი s' ნულის ტოლი აღმოჩნდება, რადგანაც
სინათლის სიგნალით ერთმანეთთან დაკავშირებული ნებისმიერი ორი ხდომილებისთვის ინტერვალი ნულის ტოლია.
ლორენცის გარდაქმნებიდან კოორდინატებისა და დროისათვის შიეძლება მივიღოთ სიჩქარეების შეკრების რელატივისტური კანონი. ვთქვათ, მაგალითად K' ათვლით სისტემაში x' ღერძის გასწვრივ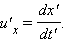 
სიჩქარით მოძრაობს ნაწილაკი. ნაწილაკის სიჩქარის u'x და u'z მდგენელები ნულის ტოლია. K სისტემაში ამ ნაწილაკის სიჩქარე ტოლია 
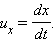. ლორენცის გარდაქმნის ფორმულებიდან დიფერენცირების ოპერაციის გამოყენებით შეიძლება მივიღოთ:
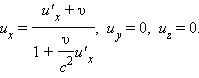
ეს თანაფარდობები სიჩქარეების შეკრების რელატივისტურ კანონს გამოსახავს. იმ შემთხვევისთვის, როცა ნაწილაკი პარალელურად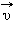 
ფარდობითი სიჩქარით მოძრაობს K და K' ათვლის სისტემებში.
როცა υ << c რელატივისტური ფორმულები კლასიკური მექანიკის ფორმულებში გადადიან:
ux = u'x + υ, uy = 0, uz = 0.
თუ სინათლის იმპულსი K' სისტემაში x' ღერძის გასწვრივ სიჩქარით u'x = c ვრცელდება, მაშინ K სისტემაში ux სიჩქარისათვის მივიღებთ
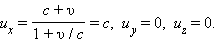
ამგვარად, K ათვლის სისტემაში სინათლის იმპულსი ასევე, x ღერძის გასწვლივ c სიჩქარით ვრცელდება, რაც თანხმობაშია სინათლის სიჩქარის ინვარიანტულობის პოსტულატთან.