წინა თავში მოყვანილია ფორმულები რმლებიც რეზისტორის, კონდენსატორისა და ინდუქციურობის კოჭასათვის ცვლადი დენისა და ძაბვის ამპლიტუდებს შორის კავშირს იძლევა:
(*)
ეს ფორმულები გარეგნულად მუდმივი დენის წრედის უბნისთვის ომის კანონს მოგვაგონებს, მაგრამ ახლა მასში შედიან არა წრედის უბნის მუდმივი დენისა და ძაბვის მნიშვნელობები, არამედ ცვლადი დენისა და ძაბვის ამპლიტუდების მნიშვნელობები.
(*) ფორმულები გამოსახავენ ომის კანონს ცვლადი დენის წრეისათვის, რომელიც R, L და C ელემენტებიდან ერთ-ერთს შეიცავს. ფიზიკურ სიდიდეებს R, 
და ωL რეზისტორის აქტიური წინაღობა, კონდენსატორის ტევადობითი წინაღობა და კოჭას ინდუქციური წინაღობა ეწოდებათ.
წრედის უბანში ცვლადი დენის გავლისას ელექტრომაგნიტური ველი ასრულებს მუშაობას და წრედში ჯოულის სითბო გამოიოფა. ცვლადი დენის წრედის მეყსეული სიმძლავრე დენის და ძაბვის მეყსეულ მნიშვნელობათა ნამრავლის ტოლია: p = J · u. პრაქტიკულ ინტერესს ცვლადი დენის პერიოდის განმავლობაში სიმძლავრის საშუალო მნიშვნელობა იწვევს
აქ I0 და U0 – წრედის მოცემულ უბანზე დენისა და ძაბვის ამპლიტუდათა მნიშვნელობებია, φ – დენსა და ძიბვას შორის ფაზათა წანაცვლება. ხაზი საშუალო მნიშვნელობას ნიშნავს. თუ წრედის უბანი მხოლოს R წინარობის რეზისტორს შეიცავს, მაშინ ფაზათა წანაცვლება φ = 0:
იმისათვის, რომ ეს გამოსახულება გარეგნულად ემთხვეოდეს მუდმივი დენისთვის სიმძლავრის ფორმულას, შემოაქვთ დენის ძალისა და ძაბვის მომქმედი ან ეფექრური მნიშვნელობის ცნება:
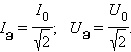
რეზისტორის შემცველი წრედის უბნის სიმძლავრე ცვლადი დენისთვის ტოლია
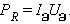
თუ წრედის უბანი შეიცავს მხოლოდ C ტევადობის კონდენსატორს, მაშინ ფაზის წანაცვლება დენსა და ძაბბას შორის 
. ამიტომ
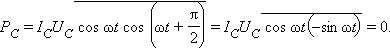
ანალოგიურად შეიძლება ვუჩვენოთ, რომ PL = 0.
ამგვარად, ცვლადი დენის წრედის სიმძლავრე მხოლოს აქტიურ წინაღობაზე გამოიყოფა. კონდენსატორზე და ინდუქციურობის კოჭაზე ცვლადი დენის საშუალო სიმძლავრე ნულის ტოლია.
ახლა განვიხილოთ ელექტრული წრედი, რომელიც მიმდევრიბით შეერთებული რაზისტორის, კონდენსატორისა და კოჭასაგან შედგება. წრედი ω სიხშირის ცვლადი დენის წყაროსთანაა მიერთებული. წრედის ყველა მიმდევრობით შეერთებულ უბანზე ერთნაერი დენი გადის. გარე წყაროს ძაბვასა e (t) და დენს J (t) შორის წარმოიშვება რაღაც φ კუთხის ტოლი ფაზის წანაცვლება. ამიტომ შეიძლება დაიწერის
J (t) = I0 cos ωt; e (t) = 
0 cos (ωt + φ).
დენისა და ძაბვის მაყსეულ მნიშვნელობათა ასეთი ჩანაწერი ვექტორულ დიაგრამას (ნახ. 2) შეესაბამება. ცვლადი დენის მიერ განვითარებული საშუალო სიმძლავრე ტოლია
როგირც ვექტორული დიაგრამიდავ ჩანს, UR = 
0 · cos φ, ამიტომ 
. აქედან გამომდინარე, წაყროს მთელი სიმძლავრე რეზისტორზე ჯოულის სითბოს სახით გამოიყოფა, რაც ზემოთ გაკეთებულ დასკვნას ამტკიცებს.
წინა თავში მოყვანილი იყო RLC-წრედში დენისა I0 და ძაბვის 0 ამპლიტუდებს შორის დამოკიდებულება:
სიდიდეს
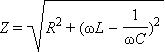
ცვლადი დენის წრედის სრულ წინაღობას უწოდებენ. დენისა და ძაბვის ამპლიტუდებს შორის დამოკიდებულების გამომსახველი ფორმულა შეიძლება ჩაიწეროს შემდეგი სახით
ZI0 = 0. (**)
ამ თანაფარდობას უწოდებენ ომის კანონს ცვლადი დენის წრედისათბის. ამ პარაგრაფის დასაწყისში მოყვანილი (*) ფორმულა, გამოსახავს (**) ომის კანონის კერძო სახეს.
სრული წინაღობის ცნება ცვლადი დენიდ წრედის გათვლისას მნიშვნელოვან როლს ასრულებს. წრედის სრული წინაღობის განსაზღვრისათვის ბევრ შემთხვევაში მოსახერხებელია ვექტორული დიაგრამის მეთოდის გამოყენება. მაგალითისთვის განვიხილოთ პარალელური RLC-კონტური, რომელიც ცვლადი დენის გარე წყარისთანაა მიერთებული (ნახ. 1).
ნახ. 1.
პარალელური RLC-კონტური
ვექტორული დიაგრამის აგებისას უნდა გავითვალისწინოთ, რომ პარალელური შეერთებისას ყველა R, C და L ელემენტში ძაბვა ერთნაერია და გარე წყაროს ძაბვის ტოლია. წრედის სხვადასხვა შტოში გამავალი დენები გამსხვავდებიან არა მარტო ამპლიტუდების მნიშვნელობებით, არამედ მოდებული ძაბვის მიმართ ფაზის წანაცვლებითაც. ამიტონ წრედის სრული წინაღობა არ შეიძლება გამოითვალოს პარალელური წრედის კანონების მიხედვით. პარალელური RLC-კონტურის ვექტორული დიაგრამა ნახ. 2-ზეა გამოსახული.
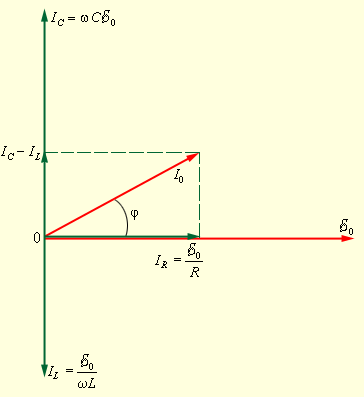
ნახ. 2.
პარალელური RLC-კონტურის ვექტორული დიაგრამა
დიაგრამიდან გამოდის:
ამიტომ პარალელური RLC-კონტურის სრული წინაღობა გამოისახება თანაფარდობით
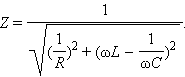
პარალელური რეზონანსისას (ω2 = 1 / LC) სრული წინაღობის მაქსიმალურ მნიშვნელობა რეზისტორის აქტიური წინაღობის ტოლია:
Z = Zmax = R.
დენს და ძაბვას შორის ფაზის წანაცვლება φ პარალელური რეზონანსისას ნულის ტოლია.