{loadnavigation}
ნიუტონის კლასიკური მექანიკა მშვენივრად აღწერს მცირე (υ << c) სიჩქარეების მქონე მაკროსხეულების მოძრაობას. არარელატივისტურ ფიზიკაში ერთიანი მსოფლიო დროის არსებობა აშკარა ფაქტად იყო მიღებული. კლასიკური მექანიკას სფუძვლად უდევს ფარდობითობის მექანიკური პრინციპი (ან გალილეის ფარდობითობის პრინციპი): მექანიკის კანონები ერთნაერია ათვლის ყველა ინერციულ სისტემაში. ეს პრინციპი ნიშნავს, დინამიკის კანონები ინვარიანტულია (ე.ი. უცვლელია) გალილეის გარდაქმნების მიმართ, რომელიც საშუალებას იძლევა გამოითვალოს მოძრავი სხეულის კოორდინატები ერთ ინეციულ სისტემაში (K), თუ მოცემულია ამ სხეულის კოორდინატები მეორე ინერციულ სისტემაში (K'). კერძო შმთხვევაში, როცა K' სისტემა K სისტემის ღერძის გასწვრივ მისი დადებითი მიმართილებით υ სიჩქარით მოძრაობს (ნახ. 1), გალილეის გარდაქმნებს აქვთ სახე:
x = x' + υt, y = y', z = z', t = t'.
იგულისხმება, რომ საწყის მომენტში ორივე სისტემის სათავე ერთმანეთს ემთხვევა.
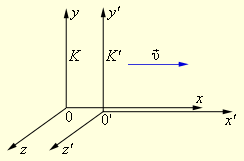
ნახ. 1.
ათვლის ორი K და K' ინერციული სისტემა
გალილეის გარდაქმნებიდან გამოდის ერთი ინერციული სისტემიდან მეორეზე გადასვლისას სიჩქარეების გარდაქმნის კლასიკური კანონი:
ux = u'x + υ, uy = u'y, uz = u'z.
სხეულის აჩქარება ყველა ინერციულ სისტემაში ყოველთვის ერთნაერია:

აქდან გამომდიმარე კალასიკურ მექანიკაში მოძრაობის განტოლება (ნიუტონის მეორე კანონი) 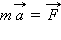 არ იცვლის სახეს ერთი ინერციული სისტემიდან მეორეში გადასვლისას.
არ იცვლის სახეს ერთი ინერციული სისტემიდან მეორეში გადასვლისას.
XIX საუკუნის ბოლოს დაგროვება დაიწყო ცდისეულმა ფაქტებმა, რომლებიც კლასიკური მექანიკის კანონებს ეწინააღმსეგებოდნენ. დიდი სირთულეები წარმოიშვა სინათლის გავრცელების ნიუტონის მექანიკით ახსნის მცდელობისას. იმის დაშვება, რომ სინათლე განსაკუთრებულ გარემოში - ეთერში - ვრცელდება, მრავალმა ექსპერიმენტმა უარყო. ამერიკელმა ფიზიკოსმა ა.მაიკელსონმაა.მაიკელსონმა 1881 წელს ჯერ დამოუკიდებლად, შემდეგ კი ე.მორლისთან ერთად 1887 წელს ინტერფერენციული მეთოდით ცდილობდა აღმოეჩინა დედამიწის მოძრაობა ეთერის მიმართ („ეთერის ქარი“). მაიკელსონ-მოპლის ცდის გამარტივებული სქემა ნახ. 2-ზეა მოცემული.
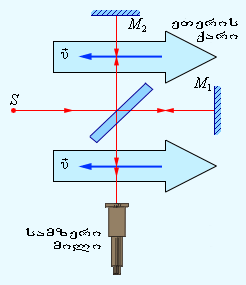
ნახ. 2.
მაიკელცინ-მოპლის ინტერფერენციული ცდის გამარტივებული სქემა. \(\vec{v}\) – დედამიწის ორბიტული სიჩქარე
ამ ცდაში მაიკელსონის ინტერფერომეტრის ერთ-ერთი მხარი დედამიწის ორბიტული სიჩქარის (υ = 30 კმ/წმ) პარალელურადაა მიმართული. შემდეგ ხელსაწყო ბრუდეაბა 90°-ით, და ორბიტული სიჩქარის გასწვრივ ორიენტირებული ახლა მეორე მხარი აღოჩნდება. გამოთვლებმა აჩვენეს, რომ უძრავი ეთერი რომ არსებობდეს, შემობრუნებისას ინტერფერენციული ზოლები (υ / c)2-ს პროპორციულ მანძილზე უნადა გადანაცვლებულიყვნენ. მაიკელცინ-მოპლის ცდამ, რომელიც არაეთხელ განმეორდა სულ უფრო მზარდი სიზუსტით, უარყოფითი შედეგი აჩვენა. მაიკელსონ-მოპლის ცდის შედეგების ანალიზმა და რამოდენიმე სხვა ექსპერიმენტმა შესაძლებელი გახადა დაესკვნათ, რომ წარმოდგენა ეთერზე, როგორც გარემოზე, რომელშიც სინათლის ტალღები ვრცელდებიან მცდარი იყო. აქედან გამომდინარე, სინათლისათვის არ არსებობს გამორჩეული (აბსოლუტური) ათვლის სისტემა. დედამიწის ორბიტაზე მოძრაობა არ მოქმედებს დედამიწაზე მიმდინარე ოპტიკურ მოვლენებზე.
სივრცისა და დროის შესახებ წარმოდგენის განვითარებაში გამორჩეული როლი მაქსველის თეორიამ შეასრულა. XX საუკუნის დასაწყისში თეორია საყოველთაოდ მიღებული გახდა. მაგრამ მაქსველის თეორიიდან გამოდის, რომ ელექტრომაგნიტური ტალღების გავრცელების სიჩქარეს ნებისმიერ ინერციულ სისტემაში ერთიდაიგივე მნიშვნელიბა აქვს, რომელიც ვაკუუმში სინათლის სიჩქარის ტოლია. ეს ნიშნავს, რომ განტოლება, რომელიც ელექტრომაგნიტური ტალღების გავრცელებას აღწერს, ინვარიანტული არ არის გალილეის გარდაქმნების მიმართ. თუ ელექტრომაგნიტური ტალღა (კერძოდ, სინათლე) K' სისტემაში ვრცელდება (ნახ. 1) x' ღერძის დადებითი მიმართულებით, მაშინ K სისტემაში გალილეის კინეტიკის თანახმად გავრცელდება c + υ-ით, და არა c -თი.
ამგავარად, XIX და XX საუკუნეების მიჯნაზე ფიზიკა კრიზისს განიცდიდა. გამოსავალი აინშტაინმა სივრცესა და დროზე კლასიკურ წარმოდგენებზე უარის თქმით იპოვა. ამ გზაზე უმნიშვნელოვანესი ნაბიჯი კლასიკურ ფიზიკაში გამოყენებული აბსოლუტური დროის ცნების გადასინჯვა იყო. კლასიკური წარმოდგენები, რომლებიც აშკარა და ნათელის შთაბეჭდილებას ტოვებს, სინამდვილეში არ გამართლდა. მრავალი ცნება და სიდიდე, რომლებიც არარელატივისტურ ფიზიკაში ითვლებოდა აბსოლუტურად, ე.ი. ათვლის სისტემისგან დამოუკიდებლად, ეინშტეინის ფარდობითობის თეორიაში გადაყვანილია ფარდობითობის რიგში.
რადგანაც, ყველა ფიზიკური მოვლება სივრცესა და დროში ხდება, სივრცულ-დროითი კანონზომიერების ახალ სისტემას არ შეეძლო არ შეხებოდა მთელ ფიზიკას.
ფარდობითობის სპეციალური თეორიის საფუძველში ორი პრინციპი ანუ პოსტულადი დევს, რომელიც ეაინშტაინმა ჩამოაყალიბა 1905 წელს.
- ფარდობითობის პრინციპი: ბუნების ყველა კანონი ინვარიანტულია ერთი ინერციული სისტემიდან მეორეში გადასვლის მიმართ. ეს ნიშნავს, რომ ინერციულ სისტემებში ფიზიკურ კანონებს (არა მარტო მექანიკის) ერთნაერი ფორმა აქვთ. ამგვარად, კლასიკური მექანიკის ფარდობითობის პრინციპი განზოგადდება ბუნების ყველა მოვლენაზე, მათ შორის ელექტრომაგნიტურებზეც. ამ განზოგადებულ პრინციპს აინშტაინის ფარდობითობის პრინციპი ეწოდება.
- სინათლის სიჩქარის ფარდობითობის პრინციპი: ვაკუუმში სინათლის სიჩქარე არ არის დამოკიდევული წყაროს ან დამკვირვებლის მოძრაობის სიჩქარეზე და ყველა ათვლის ინერციულ სისტემაში ერთნაერია. ფარდობითობის სპეციალურ თეორიაში სინათლის სიჩქარეს განსაკუთრებული ადგილი უჭირავს. ეს ურთიერთქმედების და სიგნალის სივრცის ერთი წერტილიდან მეორეში გადაცემის ზღვრული სიჩქარეა.
ეს პრინციპები უნდა განიხილებოდეს როგორც ცდისეული ფაქტების ერთობლიობის განზოგადება. ამ პრინციპებზე დაყრდნობით შექმნილი თეორიის შედეგები უამრავი ცდისეული შემოწმებებით დასტურდებოდა. ფარდობითობის სპეციალურმა თეორიამ გადაჭრა „აინშტაინამდე“ ფიზიკის ყველა პრობლემა და ახსნა ელექტროდინამიკისა და ოპტიკის იმ დროისათვის ცნობილი ექსპერიმენტების „ურთიერთგამომრიცხავი შედეგები. შემდგომში ფარდობითობის სპეციალური თეორია გამაგრებული იყო ექსპერიმენტული ფაქტებით, როლებიც მიღებული იყო ამაჩქარებელში სწრაფი ნაწილაკების მოძრაობის, ატომური პროცესების, ბირთვული რეაქციების და ა.შ. შესწავლისას.
ფარდობითობის სპეციალური თეორიის პოსტულატები კლასიკურ წარმოდგენებთან მკაფიო წინააღმდეგობაშია. განვიხილოთ ასეთი აზრობრივი ექსპერიმენტი: t = 0 დროის მომენტში, როცა ორი K და K' ინერციული სისტემის საკოორდინატო ღერძები ერთმანეთს ემთხვევა, კოორდინატთა საერთო სათავეში მოხდა სინათლის ხანმოკლე ანთება. t დროის განმავლობაში სისტემებმა ერთმანეთის მიმართ υt მანძილით გადაადგილდნენ, ხოლო სფერულ ტალღის ფრონტს თითოეულ სისტემაში ექნება ct რადიუსი (ნახ. 3), რადგანაც სისტემები ტოლუფლებიანნი არიან და სინათლის სიჩქარე ორივეში ტოლია c -სი.

ნახ. 3.
ფარდობითობის სპეციალური თეორიის პოსტულატების მოჩვენებითი წინააღმდეგობა.
K სისტემის დამკვირვებლისათვის სფეროს ცენტრი O წერტილში მდებარეობს, ხოლო K' სისტემის დამკვირვებლისათვის ის O' წერტილში იქნება. აქდან გამომდინარე,სფერული ფრონტის ცენტრი ერთდროულად ორ სხვადასხვა წერტილში იმყოფება!
წარმოქმნილი გაუგებრობის მიზეზი ფარდობითობის სპეციალური თეორიის პოსტულატებს შორის წინააღმდეგობაში კი არ არის, არამედ იმ დაშვებაში, რომ სფერული ტალღის ფრონტი ორივე სისტემისათვის დროის ერთსადაიმავე მომენტს განეკუთვნება. ეს დაშვება გალილეის გარდაქმნის ფორმულებშია ჩადებული, რომლის მიხედვითაც დრო ორივე სისტემაში ერთნაერად მიმდინარეობს: t = t'. აქედან გამომდინარე, აინშტაინის პოსტულატები ერთმანეთს კი არ ეწინააღმდეგებიან, არამედ გალილეის გარდაქმნებს. ამიტომაც გალილეის გარდაქმნების მაგივრად ფარდობითობის სპეციალურმა თეორიამ ერთი ინერციული სისტემიდან მეორეზე გადასასვლელად სხვა გარდაქმნის ფორმილები - ე.წ. ლორენცის გარდაქმნები გამოიყენა, რომლებიც სინათლის სიჩქარის მახლობელი სიჩქარეებისათვის, საშუალებას იძლევა აიხსნას ყველა რელატივისტური ეფექტი, ხოლო დაბალი (υ << c) სიჩქარეებისათვის კი გალილეის გარდაქმნების ფორმულებში გადადიან. ამგვარად, ახალმა თეორიამ (ფარდობითობის სპეციალურმა თეორიამ) ძველი კლასიკური თეორია კი არ უარყო, არამედ დააზუსტა მისი გამოყენების საზღვრები. ძველ და ახალ, უფრო ზოგად თეორიას, რომელიც ძველს ისე შეიცავს როგორც სასაზღვრო შემვევას, შორის კავშირს შესაბამისობის პრინციპი ეწოდება.
{loadnavigation}
ფარდობითობის სპეციალური (ან კერძო) თეორია სივრცისა და დროის თამანედროვე ფიზიკურ თეორიას წარმოსდგენს. კვანტური მექანიკის გვერდით, ფარდობითობის სპეციალური თეორია თანამედროვე ფიზიკისა და ტექნიკის თეორიულ საფუძველს წარმოადგენს. ფარდობითობის სპეციალურ თეორიას ხშირად რელატივისტურ თეორიასაც უწოდებენ, ხოლო ამ თეორიით აღწერილ სპეფიფიურ მოვლენებს - რელატივისრურ ეფექტებს. ეს ეფექტები განსაკუთრებით თცალსაჩინოდ იჩენენ თავს სხეულების სინათლის ვაკუუმში გავრცელების მახლობელი სიჩქარით ≈ 3·108 მ/წმ მოძრაობისას. ფარდობითობის სპეციალური თეორია ა.აინშტაინის მიერ იქა შექმნილი (1905 წ.). აინშტაინის, წინამორბედები, რომლებიც ძალიან ახლოს მივიდნენ ამ პრობლემის გადაწყვეტამდე იყვნენ ნიდერლანდელი ფოზოკოს ჰ.ლორენცი და დიდი ფრანგი ფიზიკუსი ა.პუანკარე.
{loadnavigation}
XIX საუკუნის დასაწყისში, როცა თ.იუნგი და ო.ფრენელი სინათლის ტალღურ თეორიაზე მუშაობდნენ, სინათლის ტალღების ბუნება უცნობი იყო. პირველ ეტაპზე ითვლებოდა, რომ სინათლე გრძივ ტალღას წარმოადგენდა, რომელიც რაღაც ჰიპოტეტურ გარემოში - ეთერში ვრცელდებოდა. ინტერფერენციისა და დიფრაქციის მოვლენების შესწავლისას საკითხს იმის შესახებ, სინათლის ტალღები გრძივი იყო თუ განივი მეორეხარისხოვანი მნიშვნელობა ჰქონდა. იმ დროს შეუძლებლად ეჩვენებოდათ, რომ სინათლე განივი ტალღაა, მექანიკურ ტალღებთან ანალოგიიდან გამომდინარე უნდა დაეშვათ, რომ ეთერი მყარი სხეული იყო (განივ მექანიკურ ტალღებს აიროვან და თხევად გარემოში გავრცელება არ შეუძლიათ).
მაგრამ ნელ-ნელა გროვდებოდა ექსპერიმენტული ფაქტები, რომლების სინათლის განივი ტალღების სასარგებლოდ მეტყველებდნენ. ჯერ კიდევ XVII საუკუნის ბოლოში აღმოჩნდა, რომ ისლანდიური შპატის კრისტალი (CaCO3) მასში გამავალ სხივსა აორებს. ამ მოვლენას ორმაგი სხივთა გარდატეხა უწოდეს (ნახ.1).
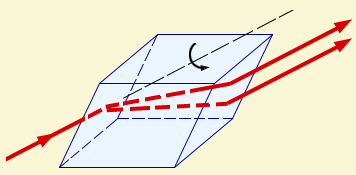
ნახ. 1.
ისლანდიური შპატის კრისტალშე სხივის გავლა (ორმაგი სხივთა გარდატეხა). თუ კრისტალს ვაბრუნებთ საწყისი სხივის მიმართ, კრისტალში გამოსული ორივე სხივი ბრუნდება
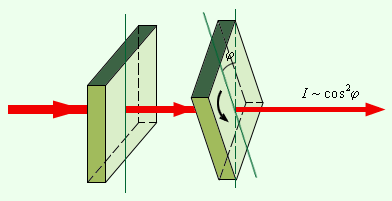
1809 წელს ფრანგმა ინჟინერბა ე.მალიუსმა აღმოაჩინა კანონი, რომელიც მის სახელს ატარებს. მალიუსის ცდებში სინათლეს ატარებნენ თურმალინის ორ ერთნაერ ფირფიტაში (მომწვანო შეფერილობის გამჭვირვალე კრისტალური ნივთიერება). ფიტფიტების ერთმანეთის მიმართ φ კუთხით მობრუნება იყო შესაძლებელი (ნახ. 2).
ნახ. 2.
მალიუსის კანონის ილუსტრაცია
გასული სინათლის ინტენსივობა cos2 φ-ის პირდაპირპროპორციული აღმოჩნდა:
I ~ cos2 φ.
არც ორმაგი სხივთა გარდატეხა და არც მალიუსის კანონი გრძივი ტალღების თეორიით არ იხსნებიდა. გრძივი ტალღებისათვის სხივის გავრცელების მიმართულება სიმეტრიის ღერძს წარმოსდგენს. გრძივ ტალღაში სხივის მართობულ სიბრტყეში ყველა მიმართულება თანაბარუფლებიანია. განივ ტალღაში (მაგალითად, რეზინის ზონარზე მორბენალ ტალღაში) რხევის მიმართულება და მისი მართობული მიმართულებები თანაბარი არ არის (ნახ. 3).

ნახ. 3.
რეზინის ზონარზე მორბენალი ტალღა. ნაწილაკები y ღერძის გასწვრივ ირხევიან. S ჭვრიტის მობრუნება ტალღის ჩაქრობას იწვევს
ამგვარად, გავრცელების (სხივის) მიმართულებით ასიმეტრია განივი ტალღის გრძივისაგან განმასხვავებელი ძირითადი მახასიათებელია. სინათლის ტალღების განივობის შესახებ პირველად მოსაზრება იუნგამა გამოთქვა 1816 წელს. ფრენელმა იუნგისგან დამოუკიდებლად ასევე წამოაყენა სინათლის ტალღების განივობის კონცეფცია, დაასაბუთა მრავალრიცხოვანი ექსპერიმენტებით და შექმნა კრისტალში სინათლის ორმაგი სხივთა გარდატეხის თეორია.
XIX საუკუნის 60-იან წლებში სინათლის ცნობილი სიჩქარის ელექტრომაგნიტური თალღების სივრცული გავრცელების სიჩქატესთან დამთხვევის საფუძველზე მაქსველმა დაასკვნა, რომ სინათლე ელექტომაგნიტური ტალღაა. ამ დროისათვის სინათლის ტალღების განივობა უკვე ექსპერიმენტულად იყო დასაბუთებული. ამიტომ, მაქსველი სამართლიანად თვლიდა, რომ ელექტრომაგნიტური ტალღების განივობა სინათლის ტალღების ელექტრომაგნიტური ბუნების კიდევ ერთი უმნიშვნელოვანესი დასაბუთებაა.
სინათლის ელექტრომაგნიტურმა თეორიამ მწყობრი სახე მიიღო, რამდენადაც არ იყო ტალღის გავრცელებისათვის აუცილებელი განსაკუთრებული გარემოს - ეთერის შემოღების აუცილებლობა.
ელექტრომაგნიტურ ტალღაში \(\vec{E}\) და \(\vec{B}\) ვექტორები ურთიერთმართობულია და ტალღის გავრცელების მართობულ სიბრტყეში მგებარეობენ (ნახ. 3). სინათლის ნივთიერებასთან ურთიერთქმედების ყველა პროცესში ძირითად როლს ელექტრული \(\vec{E}\) ვექტორი ასრულებს, ამიტომაც მას სინათლეს ვექტორს უწოდებენ. თუ ელექტრომაგნიტური ტალღების გავრცელებისა სინათლის ვექტორი ორიენტაციას ინარჩუნებს, ასეთ ტალღას წრფივად პოლარიზებულს უწოდებენ (ტერმინი პოლარიზაცია მალიუსის მიერ იყო შემოტანილი განივი ტალღების შესწავლისას). სიბრტყეს, რომელშიც სინათლის ვექტორი \(\vec{E}\) ირხევა, რხევის სიბრტყეს უწოდებენ (yz სიბრტყე ნახ. 2.6.3-ზე), ხოლო სიბრტყეს, რომელშიც ირხევა \(\vec{B}\) ვექტორი - პოლარიზაციის სიბრტყე ეწოდება ( xz სიბრტყე ნახ. 2.6.3-ზე).
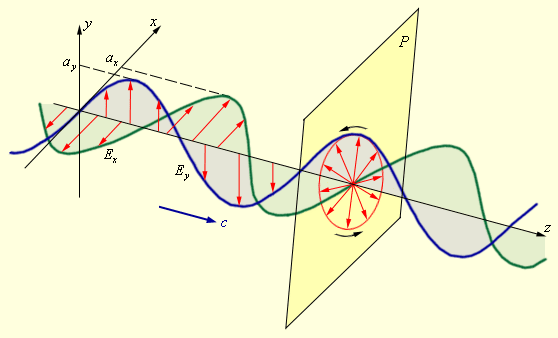
თუ ერთიდაიგივე მიმართულების ორი მონოქრომატული ერთმანეთის მართობულ სიბრტყეებში პოლარიზებული ტალღა ვრცელდება, მათი შეკრების შემთხვევაში წარმოიქმნემა ელიფსურად პოლარიზებული ტალღა (ნახ. 4).
ნახ. 4.
ორი ერთმანეთის მართობულ სიბრტყეებში მდებარე პოლარიზებული ტალღის შეკრება და ელიფსურად პოლარიზებული ტალღის წარმოქმნა
ელიფსურად პოლარიზებული ტალღის ნებისმიერ, ტალღის გავრცელების მართობულ სიბრთყეში ჯამური ვექტორის ბოლო სინათლის რხევის ერთი პერიოდის განმავლობაში ერთ ელიფსს შემოსწერს, რომელსაც ელიფსურ პოლარიზაციას უწოდებენ. ელიფსის ფორმა და ზომები წრფივად პოლარიზებული ტალღების ax და ay ამპლიტუდებითა და მათ შორის ფაზათა სხვაობით განისაზღვრება. ელეიფსური პოლარიზაციის კერძო შემთხვევას წრიული პოლარიზაცია წარმოადგრნს (ax = ay, Δφ = ± π / 2).
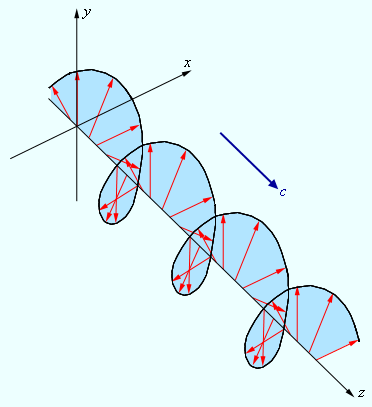
ნახ. 5 ელიფსურად პოლარიზებული ტალღების სივრცულ სტუქტურაზე იძლევა წარმოდგენას.
ნახ. 5.
ელიფსირად პოლარიზებული ტალღის ელიფსური ველი
წრფივად პოლარიზებულ სინათლეს ლაზერული წყარო იძლევა. სინათლე პოლარიზებული შეიძლება აღმოჩნდეს არეკვლის ან გაბნების შემთხვევაში. კერძოდ, ცისფერი სინათლე ცაზე ნაწილობრივ ან სრულად პოლარიზებულია. მაგრამ, ჩვეულებრივი წყაროების სინათლე (მაგალითად, მზის სინათლე, ვარვარების ნათურის სხივი და ა.შ.) პოლარიზებული არ არის. ასეთი წყაროების სინათლე ყოველ მომენტში შედგება აურაცხელი რაოდენობის, დამოუკიდებალად გამომსხივებადი, ატომების წვლილისაგან, რომელთა მიერ გამოსხივებული ტალღების სინათლის ვექტორები სხვდასხვანიერადაა ორიენტირებული. ამიტომაც ჯამური ტალღის \(\vec{E}\) ვექტორის ორიენტაცია დროში უწესრიგოს იცვლება, საშუალოდ რხევის ყველა მიმართულება თანაბარუფლებიანი აღმოჩნდება. პოლარიზაციის არ მქონე სინათლეს ბუნებრივ სინათლეს უწოდებენ.
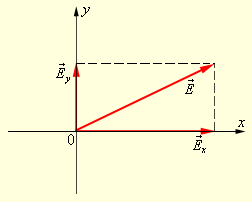
დროის ყოველ მომენტში \(\vec{E}\) ვექტორი შეიძლება დაგეგმილდეს ორ ურთიერთმართობულ ღერძზე (ნახ. 6).
ნახ. 6.
\(\vec{E}\) ვექტორის ღერძებზე დაშლა
ეს ნიშნავს, რომ ნებისმიერი ტალღა (პოლარიზებული და პოლარიზაციის არ მქონე) შეიძლება წარმოვიდგინოთ ორი ურთიერთმართობული მიმართულებით, წრფივად პოლარიზებული ტალღა: \(\vec{E(t)}=\vec{E_{x}(t)}+\vec{E_{y}(t)}\). მაგრამ, პოლარიზებულ ტალღაში ორივე Ex (t) და Ey (t) მდგენელი კოჰერენტულია, ხოლო არაპოლარიზებულის დროს - არაკოჰერენტული, ე.ი. პირველ შემთხვევაში Ex (t) და Ey (t) შორის ფაზათა სხვაობა მუმივია, ხოლო მეორეში ის დროის შემთხვევით ფუნქციას წარმოადგენს.
სინათლის ორმაგი სხივთაგარდატეხა იმით აიხსნება, რომ მრავალ კრისტალურ ნივთიერებაში ურთიერთმართობული მიმართულებით წრფივად პოლარიზებული ტალღების გარდატეხის კოეფიციენტი განსხვავებულია. ამიტომაც კრისტალი მასში გამავალ სინათლეს ორ ნაწილად ყოფს (ნახ. 1). გამოსასვლელზე ორი სხივი წრფივად პოლარიზებული ურთიერთმართობული მიმართულებით. კრისტალებს, როლმებშიც ორმაგ ხსივტაგარდატეხა ხდება, ანიზოტროპულებს უწოდებენ.
\(\vec{E}\) ვექტორის ღერძებზე დაგეგმილების საშუალებით შიძლება აიხსნას მალიუსის კანონი (ნახ. 2).
მრავალი კრისტალისათვის სინათლის შთანთქმა ძლიერადაა დამოკიდებული სინათლის ტალღის ელექტრული ვექტორის მიმართულებაზე. ამ მოვლენას დიქროიზმს უწოდებენ. ეს თვისება, ნაწილობრივ, მალიუსის ცდებში გამოყენებულ თურმალინის ფირფიტასაც ახასიათებს. გარკვეული სისქისას თურმალინის ფირფიტა თითქმის სრულად შთანთქავს ურთიერთპერპენდიკულარულად პოლარიზებული ტალღებიდან ერთ-ერთს (მაგალითად,Ex) და ნაწილობრივ ატარებს მეორე ტალღას (Ey). გასული სხივის ელექტრული ვექტორის რხევის მიმართულებას ფირფიტის დაშვებულ მიმართულებას უწოდებენ. თურმალინის ფირფიტა შეიძლება გამოყენებული იქნეს, როგორც პოლარიზებული სინათლის მისაღებად (პოლარიზატორი), ასევე სინათლის პოლარიზაციის ხასიათის ანალიზისათვის (ანალიზატორი). დღეისათვის ფართოდ იყენებენ ხელოვნურ დიქროიდულ აპკებს, რომლებსაც პოლაროიდებს უწოდებენ. პოლაროიდები დაშვებული პოლარიზაციის ტალღას თითქმის სრულად ატარებენ ხოლო მართობული მიმართულებით ოილარიზებულ ტალღას არ ატარებენ. ამგვარად, პოლაროედები შეიძლება იდეალურ პოლარიზაციულ ფილტრებად ჩაითვალონ.
განვიხილოთ ბუნებრივი სინათლის მიმდევრობითი გავლა ორ იდეალურ П1 და П2 პოლაროიდში (ნახ. 7), რომელთა დაშვებული მიმართულებები ერთმანეთის მიმართ გარკვეული φ კუთხითაა მიმართული. პირველი პოლაროიდი პოლარიზატორის როლს ასრულებს. ის ბუნებრივ სინათლეს წრფივად პოლარიზებულად გარდაქმნის. მეორე პოლარიზატორი მასაძე დაცემული სინათლის ანალიზისთვის გამოიყენება.

ნახ. 7.
ბუნებრივი სინათლის ორ იდეალურ პოლაროიდში გავლა. yy' – პოლაროიდის დაშვებული მიმართულებაა.
თუ პირველ პოლაროიდში გავლის შემდეგ წრფივად პოლარიზებული ტალღის ამპლიტიდას 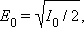 -ით ავღნიშნავთ, მაშინ მეორე პოლარიზატორის მიერ გატარებული ტალღის ამპლიტუდა E = E0 cos φ. აქედან გამომდინარე, მეორე პოლარიზატორიდან გამოსვლილას წრფივად პოლარიზებული ტალღის ინტენსივობა I ტოლია
-ით ავღნიშნავთ, მაშინ მეორე პოლარიზატორის მიერ გატარებული ტალღის ამპლიტუდა E = E0 cos φ. აქედან გამომდინარე, მეორე პოლარიზატორიდან გამოსვლილას წრფივად პოლარიზებული ტალღის ინტენსივობა I ტოლია
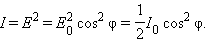
ამგვარად, მალიუსის კანონი 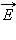 ვექტორის გეგმილებად დაშლის საფუძველზე ბუნებრივ ახსნას პოულობს ელექტრომაგნიტურ თეორიაში.
ვექტორის გეგმილებად დაშლის საფუძველზე ბუნებრივ ახსნას პოულობს ელექტრომაგნიტურ თეორიაში.
{loadnavigation}
ხილული სინათლე შედგება სხვადასხვა ტალღის სიგრძის მონოქრომატული ტალღებისაგამ. გახურებული სხეულების გამოსხივებაში (ვარვარების ნათურის ძაფი) ტალღის სიგრძეები უწყვეტად ავსებენ სინათლის მთელ დიაპაზონს. ასეთ გამოსხივებას თეთრ სინათლეს უწოდებენ. სინათლე, რომელსაც, მაგალითად, აერის განმუხტვის ნათურები და ბევრი სხვა წყარო ასხივებს, მის შემადგენლობაში შეიცავს ცალკეულ მონოქრომატულ მდგენელს ტალღის სიგრძეების გამოყოფილი მნიშვნელობებით. გამოსხივებაში მონიქრომატული კომპონენტების ერთობლიობას სპექტრს უწოდებენ. თეთრ სინათლეს იწყვეტი სპექტრი აქვს. ისეთი წყაროს გამოსხივებას, რომელშიც სინათლეს ნივთიერების ატომები ასხივებენ, დისკრეტული სპექტრი აქვს. ხელსაწყოები, რომლის საშუალებითაც გამოსხივების წყაროები სპექტრების შეისწავლება, სპექტრულ ხელსაწყოებს უწოდებენ.
გამოსხივების სპექტრად დასაშლელად უმარტივეს სპექტრულ ხელსაწყოში პრიზმა გამოიყენება (ნახ. 1). პრიზმის მოქმედება დამყარებულია დისპერსიის მოვლენაზე, ანუ ნივთიერების n გარდატეხის უნარის სინათლის λ ტალღის სიგრძეზე დამოკიდებულებაზე.
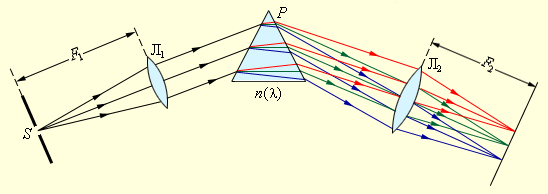
ნახ. 1.
გამოსხივების სპექტრად დაშლა პრიზმის საშუალებით
S ჭვრიტე, რომელსაც ეცემა გამოსაკვლეევი გამოსხივება, Л1 ლინზის ფოკალურ სიბრტყეში მდებარეობს. ხელსაწყოს ამ ნაწილს კოლიმატორს უწოდებენ. ლინზიდან გამოსული სინათლის პარალელურ სხივთა კონა P პრიზმას ეცემა. დისპერსიის შედეგად სხვდასხვა ტალღის სიგრძის მქონე სინათლე პრიზმიდან სხვადასხვა კუთხით გამოდის. Л2 ლინზის ფოკალურ სიბრტყეში მოთავსებულია ეკრანი ან ფოტოფირფიტა, რომელზედაც გამოსახულება მიიღება. ამის შედეგად ეკრანის სხვადასხვა ადგილებში წარმოიქმნება ჭვრიტის მსგავსი სხვადასხვა ტალღის სიგრძის გამოსახულებები. ყველა გამჭვირვალე მყარ სხეულებს (მინას. კვარცს), რომლისგანაც პრიზმები მზადდება, ხილული სინათლის დიაპაზონში n გარდატეხის მაჩვენებელი λ ტალღის სიგრძის ზრდასთან ერთად მცირდება, ამიტომაც პრიზმა საწყისი მიმართულებიდან ყველაზე მეტად ლურჯ და იისფერ სხივებს გადახრის, ყველაზე ნაკლებად კი - წითელს. მონოტონურად კლებად n (λ) დამოკიდებულებას ნორმალურ დისპერსიას უწოდებენ.
თეთრი სინათლის სპექტრად დაშლის პირველი ცდა ნიუტონმა განახორციელა (1672 წ.).
მაღალი კლასის სპექტრულ ხელსაწტოებში პრიზმის ნაცვლად დიფრაქციულ მესერს იყენებენ. მესერი მინის ან მეტალურ ზედაპირზე, სპეციალური დამყოფი მანქანით ამოგრავირებული, პერიოდულ სტრუქტურას წარმოადგენს (ნახ. 3.10.2). კარგ მესერებს ერთმანეთის პარალელური შტრიხები 10 სმ-ია, ხოლო ყოველ მილიმეტრზე 2000 შტრიხამდეა. ამასთან მესერის საერთო სიგრზე 10-15 სმ-ს აღწევს. ასეთი მესერის დასამზადებლად ყველაზე მაღალი ტექნოლოგიაა საჭირო. პრაქტიკაში უფრო უხეში, გამჭვირვალე აფსკზე დატანილი 50-100 შტრიხი მილიმეტრზე, მესერებიც გამოიყენება. დიფრაქციულ მესერად კონპაქტ-დისკის ან ძველი გრამაფონის ფირფიტის ნაწილიც შეიძლება იქნეს გამოყენებული.
ნახ. 2.
დიფრაქციული მესერი
უმარტივესი დიფრაქციული მესერი შედგება გამჭვირვალე უბნებისა (ჭვრიტეები), რომლებიც გაუმჭვირვალე შვუალუდებითაა გაყოფილი. მესერზე კოლიმატორის საშუალებით მიმართულია გამოსაკვლევი სინათლის პარალელურ სხივთა კონა. დაკვირვება მესერის უკან მოთავსებული ლინზის ფოკალურ სიბრტყეში ხვდება (ნახ. 3).
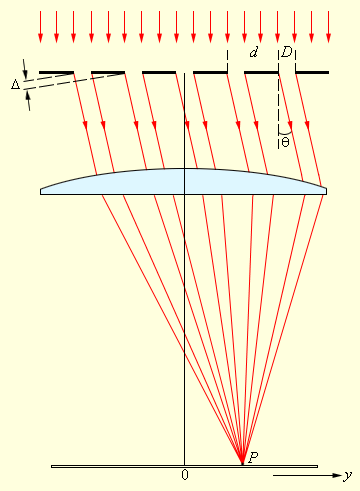
ნახ. 3.
დიფრაქციული სინათლე მესერზე
ლინზის ფოკალურ სიბრტყეში მოთავსებული ეკრანის ყოველ P წერტილში შეიკრიბება სხივები, რომლებიც ლინზამდე ერთმანეთის პარალელურები იყვნენ და დაცემული ტალღის მიმართულებით გარკვეული θ კუთხით ვრცელდებოდნენ. რხევები P წერტილში სხვადასხვა ჭვრიტეებიდან მოსული მეორადი ტალღების ინტერფერენციის შედეგს წარმოადგენს. იმისათვის, რომ P წერტილში დაიკვირვებოდეს ინტერფერენციული მაქსიმუმი, მეზობელი ჭვრიტეებიდან გამოსული ტალღებს შორის სვლათა სხვაობა Δ ტალღის სიგრძის მთელი რიცხვის ტოლი უნდა იყოს:
Δ = d sin θm = mλ (m = 0, ±1, ±2, ...).
აქ d – მესერის პერიოდი, m –მთელი რიცხვი, რომელსაც დიფრაქციული რიგის მაქსიმუმს უწოდებენ. ეკრანის იმ წერტილებში, რომლებშიც ეს პირობა სრულდება, განთავსებულია ე.წ. დიფრაქციული სურათის მთავარი მაქსიმუმები.
ლინზის ფოკალურ სიბრტყეში ნულოვანი რიგის (m = 0) მაქსიმუმიდან m -ური რიგის მაქსიმუმამდე მანძილი დიფრაქციის მცირე კუთხის შემთხვევაში ტოლია

სადაც F – ფოკუსური მანძილია.
ყრადღება მისაქცევია, რომ ლინზის ფოკალური სიბრტყის ყოველ წერტილში მესერის N ჭვრიტიდან მოსული N ტალღის ინტერფერენცია ხდება.ეს ე.წ. მრავალტალღოვანი (ან“მრავალსხივიანი“) ინტერფერენციაა. დაკვირვების სიბრტყეში სინთლის ენერგიის განაწილება მკვეთრად განსხვავდება იმისაგან, რასაც ჩვეულებრივი „ორსხივიან“ ინტერფერენციულ სქემაში აქვს ადგილი. მთავარ მაქსიმუმებში ყველა ტალღა ფაზაში მიდის, ამიტომ რხევის ამპლიტუდა N -ჯერ იზრდება, ხოლო ინტენსივობა N2-ჯერ იმ რხევასთან შედარებით, რასაც ერთი ჭვრიტიდან მომავალი ტალღა აღძრავს.
შერევისას მთავარი მაქსიმუმებიდან რხევის ინტენსივობა სწრაფად ეცემა. N ტალღამ რომ ერთმანეთი ჩააქროს, ფაზათა სხვაობა უნდა შეიცვალოს 2π / N-თი, და არა π -თი, ისე როგორც ორი ტალღის ინტერფერენციისას. ნახ. 4-ზე მოცემულია ვექტორული დიაგრამა რხევებისა, რომელიც ყველა N ჭვრიტიდან აღიძვრება იმ პირობით, რომ მეზობელ ჭვრიტეებს შორის ფაზათა სხვაობა ტოლია 2π / N, და შესაბამისად სვლათა სხვაობა ტოლია λ / N. N რხევის გამომსახველი ვექტორი ამ შემთხვევაში ჩაკეტილი მრავალკუთხედით გამოისახება. ამგვარად, მთავარი მაქსიმუმიდან მეზობელ მინიმუმში გადასვლისას სვლათა სხვაობა Δ = d sin θ უნდა შეიცვალოს λ / N -თი. ამ პირობიდან შეიძლება შეფასდეს მთავარი მაქსიმუმების კუთხური ნარევარსიგანე δθ:

აქ სიმარტივისათვის იგულისხმება, რომ დიფრაქციული კუთხე საკმარისად მცირეა. აქდან გამომდინარე,
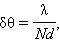
სადაც Nd – მესერის სრული ზომებია. ეს თანაფარდობა სრულ თანხმობაშია პარალელური სხივების დიფრაქციის თეორიასთან, რომლის მიხედვითაც პარალელურ სხივთა კონის დიფრაქციული განშლა ტოლია ტალღის სიგრძის ფარდობისა წინააღმდეგობის განივ ზომასთან.

ნახ. 4.
ინტერფერენციული სურათში რხევის შეკრება მაქსიმუმსა და მინიმუმში: a –ორი ტალღის ინტერფერენცია; b – N ტალღის ინტერფერენცია (N=8)
შესაძლებელია მნიშვნელოვანი დასკვნის გაკეთება: მესერზე სინათლის დიფრაქციისას მთავარი მაქსიმუმები ძალიან ვიწროებია. ნახ. 5 იძლევა წარმოდგენას თუ როგორ იცვლება მთავარი მაქსიმუმების სივიწროვე მესერის ჭვრიტეების რიცხვის გაზრდით.

ნახ. 5.
ინტენსივობის განაწილემა ჭვრიტეების სხვადასხვა რიცხვის მქონე მესერებზე მონოქრომატული სინათლის დიფრაქციის შემთხვევაში. I0 – ერთ ჭვრიტეზე სინათლის დიფრაქციისას რხევის ინტენსივობა
მესერის ფორმულიდან გამომდინარე, მთავარი მაქსიმუმების მდებარეობა (ნულოვანის გარდა) λ ტალღის სიგრძეზეა დამოკიდებული. ამიტომას მესერს შეუძლია გამოსხივების სპექტრად დაშლა, ე.ი. ის სპექტრულ ხელსაწყოს წარმოადგენს. თუ მესერს არამონოქრომატული გამოსხივება ეცემა, მაშინ დიფრაქციის ყოველ რიგში (ანუ m -ის ყოველი მნიშვნელობისთვის) საკვლევის გამოსხივების სპექტრი წარმოიშვება, ამასთან სპექტრის იისფერი ნაწილი ნულოვანი რიგის მაქსიმუმისკენაა განთავსებული. ნახ. 6-ზე თეთრი სინათლისთვის სხვადასხვა რიგის სპექტრებია გამოსახული. ნულოვანი რიგის მაქსიმუმი შეუფერავი რჩება.
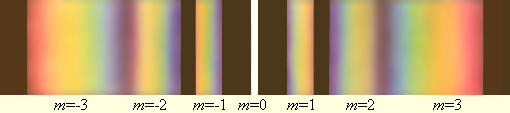
ნახ. 6.
თეთრი სინათლის დაშლა დიფრაქციული მესერის სასუალებით
დიფრაქციული მესერის საშუალებით შესაძლებელია ტალღის სიგრძის ძალიან ზუსტი გაზომვა. თუ მესერი d პერიოდი ცნობილია, მაშინ ტალღის სიგრძის განსაზღვრა m -ური რიგის სპექტრში არჩეული ხაზის მიმართულების შესაბამისი θm კუთხის გაზომვამდე დაიყვანება. პრაქტიკაში ჩვეულებრივ პირველი და მეორე რიგის სპექტრები გამოიყენება.
თუ საკვლევის გამოსხივების სპექტრში ორი სპექტრული ხაზია λ1 და λ2 ტალღის სიგრძეებით, მაშინ მესერს ყოველ სპექტრულ რიგში (გარდაm = 0) შეუძლია ერთი ტალღის მეორისაგან განცალკევება.
დიფრაქციული მესერის ერთ-ერთ უმნიშვნელოვანეს მახასიათებელს მისი გარჩევის უნარი წარმოადგენს, რომელიც მოცემული მესერის საშუალებით λ და λ + Δλ ტალღის სიგრძეების მქონე ორი ახლომდებარე სპექტრული ხაზის გარჩევის შესაძლებლობას ახასიათებს. სპექტრული გარჩევის უნარი R ეწოდება λ ტალღის სიგრძის ფარდიბას Δλ-ს მინიმალურ შესაძლო მნიშვნელობასთან, ანუ

სპექტრული ხელსაწყოების გარჩევის უნარი, და კერძოდ, დიფრაქციული მესერისა, ისევე როგორც ოპტიკური ინსტრუმენტების (ტელესკოპი, მიკრისკოპი) ზღვრული გარჩევა, სინათლის ტალღური ბუნებით განისაზღვრება. ითვლება, რომ ორი ახლომდებარე ხაზის m -ური რიგის სპექტრში განირჩევა, თუ λ + Δλ ტალღის სიგრძისათვის მთავარი მაქსიმუმი λ ტალღის სიგრძის მთავრი მაქსიმუმისაგან მტავარი მაქსიმუმის ნახევარსიგანეზე ნაკლებით, ე.ი. δθ = λ / Nd-ით. ფაქტიურად ეს სპექტრული ხელსაწოებისათვის გამოყენებული რელეის კრიტერიუმია. მესერის ფორმულიდან გამოდის, რომ:
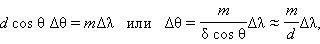
სადაც Δθ – m -ური რიგის სპექტრში ორი ახლომდებარე, ტალღის სირძეებს შორის Δλ სხვაობით, ხაზის მთავარ მაქსიმუმებს შორის კუთხური მანძილია. სიმარტივისათვის იგულისხმება, რომ დიფრაქციის კუთხეები მცირეა (cos θ ≈ 1). Δθ და δθ- ს გატოლებით მესერის გარჩევის ძალის შეფასებას მივიღებთ:

ამგვარად, დიფრაქციული მესერის ზღვრული გარჩევა მხოლოდ სპექტრის რიგზე და მესერის პერიოდების N რიცხვზეა დამოკიდებული.
ვთქვათ მესერის პერიოდია d = 10–3 მმ, მისი სიგრძე L = 10 სმ. მაშინ, N = 105 (ეს კარგი მესერია). მეორე რიგის სპექტრისათვის მესერის გარჩევის უნარი ტოლია R = 2·105. ეს ნიშნავს, რომ ტალღის სიგრძეების მინიმალურად დასაშვები ინტერვალი სპექტრის მწვანე უბანში (λ = 550 ნმ) ტოლია Δλ = λ / R ≈ 2,8·10–3 ნმ. იგივე პირობებში d = 10–2 მმ и L = 2 სმ მესერის ზღვრული გარჩევა იქნებოდა Δλ = 1,4·10–1 ნმ-ს ტოლი.
