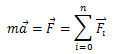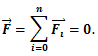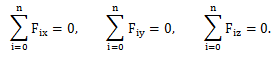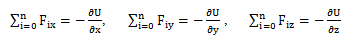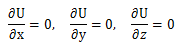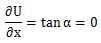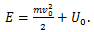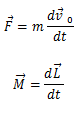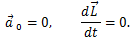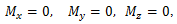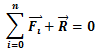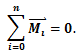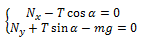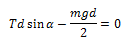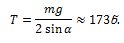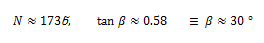მოამზადეს: დავით ხუციშვილმა და ირაკლი მღებრიშვილმა

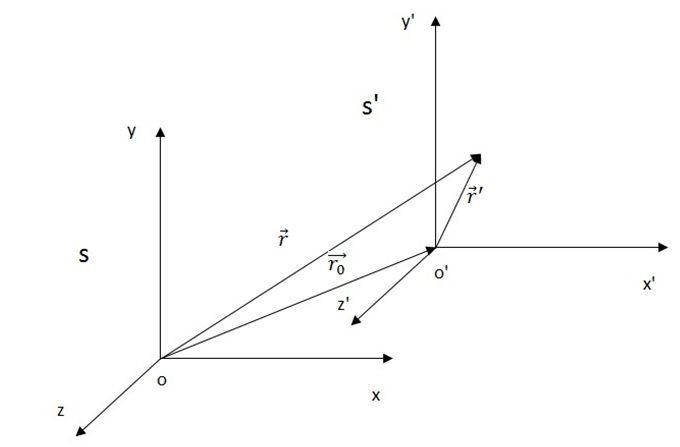
ნიუტონის I და II კანონები მართებულია მხოლოდ ათვლის ინერციულ სისტემებში. ვთქვათ, S წარმოადგენს ათვლის ინერციულ სისტემას, ხოლო S' - სისტემას, რომელიც მოძრაობას S სისტემის მიმართ \(\vec{v}_{0}\) სიჩქარით, ისე რომ მისი ღერძები S სიტემის ღერძების პარალელურია. ანუ, S' სისტემა მოძრაობს S სისტემის მიმართ გადატანით, \(\vec{v}_{0}\) სიჩქარით (ნახ. 1).

ნახ. 1

თუ ნებისმიერი M წერტილის რადიუს–ვექტორებს S და S' სისტემებში შესაბამისად აღვნიშნავთ \(\vec{r}\) და \(\vec{r}_{'}\)– ით, მაშინ ნახაზიდან გვექნება, რომ

\(\vec{r}=\vec{r}^{'}+\vec{r}_{0}\)

თუ ამ ტოლობას დროით გავაწარმოებთ, მივიღებთ

\(\vec{v}=\vec{v}^{'}+\vec{v}_{0}\)           (1)

სადაც \(\vec{v}\) და \(\vec{v}'\) მატერიალური M წერტილის სიჩქარეებია შესაბამისად S და S' სისტემათა მიმართ.

(1) წარმოადგენს სიჩქარეთა შეკრების გალილეის კანონს და ამ ტოლობის დროით გაწარმოება გვაძლევს დამოკიდებულებას S და S' სისტემებში M წერტილის აჩქარებებს შორის:

\(\vec{a}=\vec{a}^{'}+\vec{a}_{0}\)           (2)

ა) ვთქვათ S' სისტემა ინერციულია. ეს ნიშნავს, რომ იგი მოძრაობს ინერციული S სისტემის მიმართ თანაბრად და წრფივად, ანუ \(\vec{a}_{0}=\frac{\mathrm{d} \vec{v}_{0}}{\mathrm{d} t}=0\), მაშინ (2)–დან

\(\vec{a}=\vec{a}^{'}\)                 (3)

ორივე სისტემაში მატერიალურ წერტილზე მოქმედი ძალები ერთნაირია \(\vec{F}=\vec{F}^{'}\), ვინაიდან მოცემულ წერტილზე მოქმედი ძალა განისაზღვრება მის გარემომცველ სხეულთა მდებარეობით და მოქმედების ხასიათით, რაც კოორდინატთა სისტემის შერჩევაზე არ არის დამოკიდებული.

მივიღეთ, რომ თუ ერთ–ერთ ინერციულ სისტემაში წერტილის აჩქარება გამოწვეულია მხოლოდ გარემომცველ სხეულებთან მისი ურთიერთქმედებით, მაშინ ნებისმიერ სხვა ინერციულ სისტემაში მასზე იმოქმედებს იგივე ძალა და მიანიჭებს მას იმავე აჩქარებას. თუ კერძოდ, S სისტემაში M მატერიალურ წერტილზე მოქმედი ძალა ნულის ტოლია, \(\vec{F}=0\) და მაშასადამე \(\vec{a}=0\), მაშინ S' სისტემაშიც \(\vec{F}'=0\) და \(\vec{a}'=0\). აქედან გამომდინარეობს დასკვნა, რომ ინერციული S და S' სისტემები მექანიკური თვალსაზრისით სრულიად ეკვივალენტურია.

ბ) ვთქვათ, S' სისტემა არაინერციულია, ანუ აჩქარებული, \(\vec{v}_{0}\)≠const და მაშასადამე \(\vec{a}_{0}\) ≠ 0. მაშინ (2)–დან

\(\vec{a}^{'}=\vec{a}-\vec{a}_{0}\)

ხოლო

\(m\vec{a}^{'}=m\vec{a}-m\vec{a}_{0}\)

მაგრამ \(m\vec{a}=\vec{F}'=\vec{F}\) ამიტომ გამოდის, რომ

\(m\vec{a}^{'}=\vec{f}'-m\vec{a}\)    (4)

ე.ი. არაინერციულ სისტემაში ნიუტონის მეორე კანონი მართებული არ რჩება (m მასის მატერიალურ წერტილზე ამ სისტემაში მოქმედი ძალა \(\vec{F}'\) არ უდრის მასისა და ამ სიტემაში წერტილის აჩქარების ნამრავლს, \(m\vec{a}^{'}\neq \vec{f}'\))

აქედან გამომდინარეობს ორი დებულებიდან ერთ–ერთის დაშვების აუცილებლობა: ან არაინერციულ სისტემაში წერტილის აჩქარება გამოწვეულია არამარტო ძალებით, ან აჩქარება პროპორციულია მოქმედი ძალების ტოლქმედის, მაგრამ ამ ძალების გამომწვევი მიზეზი, სხეულთა მოქმედების გარდა, შეიძლება იყოს სხვა რაღაც, რაც საჭიროებს გათვალისწინებას.

რადგან პირველი დაშვება დაკავშირებულია მექანიკის ძირითადი კანონების უარყოფასთან, ამიტომ უფრო მიზანშეწონილია მეორე დაშვება: (4)–ის საფუძველზე უნდა დავუშვათ, რომ არაინერციულ S' სისტემაში, გარდა გარემომცველი სხეულების ურთიერთქმედებით განპირობებულ \(\vec{F}'\) ძალისა, M მატერიალურ წერტილზე მოქმედებს აგრეთვე ძალა

\(\vec{F}_{i}=m(-\vec{a}_{0})\)

გამოწვეული თვით სისტემის აჩქარებით. ასეთ \(\vec{F}_{i}\) ძალას ინერციის ძალა ეწოდება. უნდა აღინიშნოს, რომ ინერციის ძალა არ გამოსახავს განხილულ მატერიალურ წერტილზე სხვა სხეულების მოქმედებას და გამოწვეულია თვით ათვლის სისტემის აჩქარებით. ინერციის ძალა უდრის მატერიალური წერტილის მასისა და სისტემის აჩქარების ნამრავლს, აღებულს მოპირდაპირე ნიშნით.

განვიხილოთ ინერციის ძალათა მოქმედების რამდენიმე მაგალითი.

განვიხილოთ დედამიწის მიმართ თანაბარაჩქარებულად და წრფივად მოძრავი ურიკა, რომლის ზედაპირზე მოთავსებულია სხეული. წარმოვიდგინოთ, რომ სხეულიც ურიკასთან ერთად მოძრაობს. სხეულზე მოქმედი ძალებია სიმძიმის ძალა, ურიკის მხრიდან მოქმედი ხახუნის ძალა და ურიკას რეაქციის ძალა (იხ. ნახ.2). დედამიწასთან დაკავშირებულ ათვლის სისტემაში სამი ძალის ტოლქმედი სხეულს ანიჭებს აჩქარებას და სხეული ურიკასთან ერთად მოძრაობს. განვიხილოთ სხეულის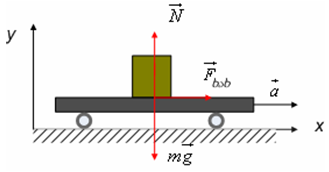 მოძრაობა ურიკასთან დაკავშირებულ ათვლის სისტემაში. ამ სისტემაში სხეული უძრავია მიუხედავად იმისა, რომ სხეულზე ჰორიზონტალური მიმართულებით მოქმედი ხახუნის ძალა არ არის გაწონასწორებული რომელიმე სხვა ძალით (ვერტიკალური მიმართულებით რეაქციის და სიმძიმის ძალები ერთმანეთს აბათილებენ). მაშასადამე ნიუტონის კანონის გამოყენებამ მიგვიყვანა წინააღმდეგობამდე. თუ წარმოვიდგენთ, რომ ურიკას ზედაპირი აბსოლუტურად გლუვია და ხახუნს ადგილი არ აქვს, მაშინ სხეული ურიკის მიმართ იმოძრავებს საპირისპირო მიმართულებით აჩქარებით მაშინ, როდესაც სხულზე მოქმედი სამი ძალიდან მხოლოდ ორი ძალა (სიმძიმის და რეაქციის) აბათილებს ერთმანეთს. ამ შემთხვევაშიც ნიუტონის კანონი  რეალობასთან წინააღმდეგობაში მოდის. ამრიგად, ეს მარტივი მაგალითი გვიჩვენებს, რომ ნიუტონის კანონები აჩქარებულად მოძრავ ათვლის სისტემაში ირღვევა.

ათვლის ინერციულ სისტემებში, როგორც ვიცით, აჩქარების გამომწვევ მიზეზს წარმოადგენს ძალა ან ძალების ტოლქმედი. ძალის საშუალებით ჩვენ რაოდენობრივად აღვწერთ სხეულების ურთიერთქმედებას. ძალის წარმოქმნის სხვა რაიმე მიზეზი, გარდა სხეულთა ურთიერთქმედებისა, არარსებობს. გარდა ამისა ორი სხეული ერთმანეთთან ურთიერთქმედებს სიდიდით ტოლი და ურთიერთსაპირისპიროდ მიმართული ძალებით. ათვლის არაინეციულ სისტემებში ამ დებულებების შენარჩუნება არ ხერხდება.

განვიხილოთ სხეულის მოძრაობა უძრავი ღერძის გარშემო თანაბრად მბრუნავ წრიულ სიბრტყეზე მყოფი დამკვირვებლის თვალსაზრისით (იხ.ნახ.3).

ეს დამკვირვებელი ცხადია არის აჩქარებულად მოძრავი და მაშასადამე ათვლის არაინერციული სისტემა. ამ დამკვირვებლისთვის დანარჩენი სამყარო მოძრაობს მის გარშემო. დაუშვათ მან ფრთხილად დადო ბურთი მბრუნავ სიბრტყეზე ისე, რომ სიბრტყის მიმართ საწყისი სიჩქარე არ მიანიჭა. სიბრტყე ჩავთვალოთ აბსოლუტურად გლუვად და ხახუნი არ მივიღოთ მხედველობაში. ნიუტონის პირველი კანონის თანახმად საწყის მომენტში უძრავად მყოფი ბურთი უნდა  დარჩეს უძრავი: ამ სხეულზე მოქმედი სიმძიმის და რეაქციის ძალები ერთმანეთს აბათილებენ. სხვა ძალა კი სხეულზე არმოქმედებს. სიბრტყეზე მყოფი დამკვირვებელი კი ხედავს, რომ ბურთი იწყებს მოძრაობას აჩქარებულად. უძრავი დამკვირვებელი, რომლის მიმართ სიბრტყე ასრულებს ბრუნვით მოძრაობას, ხედავს, რომ სხეულს აქვს ბურთის დადების წერტილის წირითი სიჩქარის ტოლი საწყისი სიჩქარე, რომლითაც სხეული აგრძელებს წრფივად და თანაბრად მოძრაობას იმ წრეწირის მხების გასწვრივ, რომელსაც ეკუთვნის ეს წერტილი. როგორც ვხედავთ ნიუტონის პირველი კანონი ირღვევა მბრუნავ სიბრტყესთან დაკავშირებულ ათვლის სისტემაში.

იმისათვის, რომ ნიუტონის კანონების სამართლიანი იყოს ათვლის არაინერციულ სისტემებშიც, უნდა დავუშვათ, რომ აჩქარებას სხეულების ურთიერთქმედების გარდა იწვევს რაღაც სხვა მიზეზიც, რომელსაც არაფერი აქვს საერთო სხეულების ურთიერთქმედებასთან და მაშასადამე ძალებთან ჩვეული აზრით. თუმცა მოხდა ისე, რომ დაშვებული იქნა ახალი ტიპის ძალის არსებობა, რომელსაც ისეთივე კავშირი აქვს აჩქარებასთან როგორც სხვა, ბუნებაში არსებულ რეალურ ძალებს. ამ ძალის შემოტანით შესაძლებელი გახდა ნიუტონის მეორე კანონის შენარჩუნება  და მას ინერციის ძალაეწოდა. ეს ძალა არ არის დაკავშირებული სხეულების ურთიერთქმედებასთან. ეს ძალა არის ფიქტიური ძალა, რომლის არსებობა დაშვებულია მხოლოდ ათვლის არაინერციულ სისტემებში. ამ ძალების არსებობა განპირობებულია მხოლოდ იმით, რომ არაინერციული ათვლის სისტემა აჩქარებულად მოძრაობს. მისმა შემოტანამ შესაძლებელი გახადა ნიუტონის პირველი და მეორე კანონების გამოყენება ათვლის არაინერციულ სისტემებშიც. ნიუტონის მესამე კანონი ასეთი სისტემებისთვის კვლავ არასამართლიანია –ი ნერციის უკუქმედება არ არსებობს.

ინერციის ძალის გათვალისწინებით  ნიუტონის მეორე კანონი სხეულისთვის, რომელიც მოძრაობს ათვლის არაინერციული სისტემის მიმართ, რაღაც a₀ აჩქარებით, ჩაიწერება შემდეგი სახით

F + F_in = ma₀,

სადაც F არის სხეულების ურთიერთქმედებით გამოწვეული ძალების ტოლქმედი, ეს უკანასკნელი სხეულს ინერციული ათვლის სისტემის მიმართ ანიჭებს a აჩქარებას და ე.ი. F=ma. ასეთნაირად ჩაწერილი განტოლებიდან ინერციის ძალისთვის მივიღებთ:

F_in = m(a₀-a)

 ადვილი დასანახია, რომ სიდიდე a'=a₀-a არის აჩქარება, რომლითაც ათვლის არაინერციული სისტემა მოძრაობს ათვლის ინერციული სისტემის მიმართ (სხეულის აჩქარება a ათვლის ინერციული სისტემის მიმართ წარმოადგენს ათვლის არაინერციული სისტემის მიმართ მისი აჩქარების a₀ და ათვლის ინერციული სისტემის მიმართ არაინერციული სისტემის აჩქარების a' ვექტორულ ჯამს). ამრიგად ინერციის ძალას აჩქარებულად მოძრავ ათვლის სისტემაში აქვს შემდეგი სახე:

F_in = -ma'

 ეს ნიშნავს, რომ ინერციის ძალა სხეულს ანიჭებს იმ აჩქარების საპირისპიროდ მიმართულ აჩქარებას, რომლითაც ათვლის არაინერციული სისტემა მოძრაობს ათვლის ინერციული სისტემის მიმართ. თუ სხეული უძრავია ათვლის არაინერციულ სისტემაში (ან მოძრაობს თანაბრად და წრფივად), მაშინ a'=a (სხეულიც მოძრაობს იგივე აჩქარებით ათვლის ინერციულისისტემის მიმართ, როგორითაც ათვლის არაინერციული სისტემა), ხოლო F_in = -ma'. თუ მიუყენებთ ნიუტონის მეორე კანონს ასეთი სახით ნახ. 3–ზე განხილულ მაგალითს ხახუნის გაუთვალისწინებლად მაშინ სხეულის მოძრაობა ურიკაზე ურიკის მოძრაობის საპირისპირო მიმართულებით გამოწვეულია მხოლოდ ინერციის ძალით (ვგულისხმობთ, რომ სიმძიმის და რეაქციის ძალები ერთმანაეთს აბათილებენ) და ეს ძალა ანიჭებს სხეულს ურიკის აჩქარების საპირისპიროდ მიმართულ აჩქარებას. ათვლის ინერციული სისტემის მიმართ კი ეს სხეული იქნება უძრავი.

 

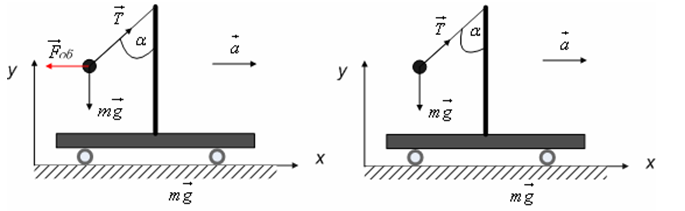
განვიხილოთრამდენიმემაგალითიდა ვნახოთთუროგორშეიძლებაერთიდაიგივემოძრაობააღვწეროთათვლისროგორცინერციულ,       ასე არაინერციულ სისტემებში. ვთქვათ ურიკა მასზე უძრავად დამაგრებული ვერტიკალური ღეროთი მოძრაობს მუდმივი a აჩქარებით (იხ. ნახ. 4). ღეროზე ჩამოკიდებულია ძაფზე დამაგრებული m  მასის ბურთულა. ურიკას აჩქარებული მოძრაობა გამოიწვევს ძაფის გადახრას ვერტიკალის მიმართ რაღაც \(\alpha\) კუთხით, ურიკასთან დამაგრებული ათვლის არაინერციულ სისტემაში ბურთულაზე მოქმედებს სამი ძალა: სიმძიმის ძალა, ძაფის დაჭიმულობის ძალადა ინერციის ძალა. რადგან ბურთულა ურიკის მიმართ  უძრავ მდგომარეობაშია (ნახ. 4), ნიუტონის მეორე კანონი ამ სისტემაში ჩაიწერება ასე:

F_in+T+mg=0

თუ გავითვალისწინებთ ინერციის ძალის მნიშვნელობას, მაშინ

-ma+T+mg=0

რაც ემთხვევა ნიუტონის მეორე კანონს ინერციული ათვლის სისტემის მიმართ:

T+mg=ma

განვიხილოთ ისევ მბრუნავი სიბრტყე და მასზე მოთავსებული სხეული. მხოლოდ გავითვალისწინოთ ხახუნი სხეულსა და სიბრტყეს შორის. ვთქვათ სიბრტყის კუთხური სიჩქარე არ არის საკმარისი იმისთვის, რომ სხეული მოწყდეს ზედაპირს. მა

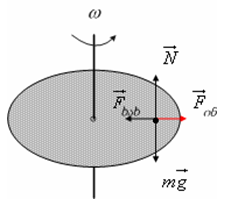
შინ სხეული ბრუნავს სიბრტყესთან ერთად. უძრავი დამკვირვებლისთვის         (ათვლის          ინერციულ სისტემაში) ნიუტონის მეორე კანონის თანახმად N+mg+Fხახ= ma სხეულს აქვს          ცენტრისკენული აჩქარება, რომელსაც მას რეალურად ანიჭებს ხახუნის ძალა (ვერტიკალური მიმართულებით აჩქარება არ გვაქვს და ძალები ერთმანეთს აბათილებენ). სიბრტყეზე მყოფი დამკვირვებლისთვის (ათვლის არაინერციული სისტემა) სხეული უძრავია. ამიტომ ნიუტონის პირველი კანონის თანახმად ინერციის ძალის გათვალისწინებით

N+ mg+ Fხახ+ Fინ= 0

სიმძიმის და რეაქციის ძალები აწონასწორებენ ერთმანეთს, ხოლო ჰორიზონტალური მიმართულებით ინერციის ძალა აწონასწორებს ხახუნის ძალას, ანიჭებს რა სხეულს ცენტრისკენული აჩქარების საპირისპიროდ მიმართულ აჩქარებას.

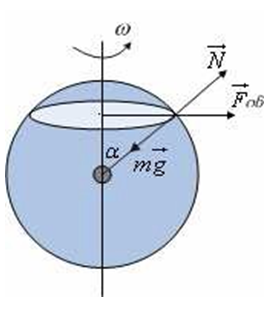
როდესაც ვსაუბრობთ ათვლის ინერციულ სისტემებზე, ვგულისხმობთ, რომ დედამიწის ბრუნვითი მოძრაობის და მისი ცენტრისკენული აჩქარების უგულებელყოფა შესაძლებელია. თუ მკაცრად ვიმსჯელებთ, მაშინ დედამიწასთან დაკავშირებული ათვლის სისტემა არაინერციულია (იხ. ნახ. 6) და აუცილებელია ინერციის ძალის გათვალისწინება სიმძიმის და დედამიწის რეაქციის ძალებთან ერთად. ინერციის ძალა სხეულს ანიჭებს აჩქარებას, რომელიც მიმართულია ცენტრიდან და სიდიდით ტოლია

F_ინ= m\(\omega ^{2}\) r

სადაც r არის აღნიშნულ განედზე მბრუნავი სხეულის ტრაექტორიის რადიუსი. ინერციის ძალის მოქმედება იწვევს იმას, რომ   სხეულისწონა   ამწერტილში ნაკლებია სიმძიმის ძალაზე.

თუ სხეული მბრუნავ სისტემაშია მოთავსებული, მაშინ ამავე სისტემაში მყოფი დამკვირვებელის თვალსაზრისით მასზე მოქმედებს ინერციის ცენტრიდანული ძალა

\(\vec{f}_{i}=m\omega ^{2}r\)

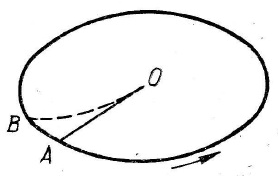
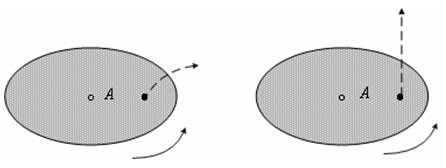
თუ მბრუნავ სისტემაში მყოფი სხეული მოძრაობს ამ სისტემის მიმართ გარკვეული სიჩქარით, მაშინ მასზე, გარდა ინერციის ცენტრიდანული ძალისა, მოქმედებს კიდევ ერთი ინერციის ძალა, რომელსაც კორიოლისის ძალა ეწოდება. ამ ძალის არსებობა შეიძლება აღმოვაჩინოთ მარტივი ცდით. განვიხილოთ ჰორიზონტალურ დისკო, რომელსაც შეუძლია ბრუნვა ვერტიკალური ღერძის ირგვლივ. გავაგოროთ ბირთვი დისკოს ცენტრისკენ, თუ დისკო არ ბრუნავს, მაშინ ბირთვი გაყვება OA-ს, მაგრამ თუ დისკოს ვაბრუნებთ (ნახ. 7) ნახაზე ნაჩვენები მიმართულებით, მაშინ ბირთვი გაჰყვება OB წირს, ამასთან მისი სიჩქარე დისკოს მიმართ შეიცვლის მიმართულებას. გამოდის რომ მბრუნავი დისკოს მიმართ ბირთვი მოძრაობს ისე, თითქოს მასზე მოქმედებს ბირთვის სიჩქარის მართობული \(\vec{f}_{k}\)  ძალა,რომელსაც კორიოლისის ძალა ეწოდება.

            თუ OA-ს გასწვრივ დისკოზე გავაკეთებთ ღარს, მაშინ ამით ვაიძულებთ ბირთვს იმოძრაოს OA მიმართულებით, ვინაიდან ბირთვის მოძრაობის დროს ამ ღარის მარჯვენა წიბო იმოქმედებს მასზე გარკვეული \(\vec{f}_{R}\) ძალით, ამიტომ დისკოსთან დაკავშირებული დამკვირვებელი დაასკვნის, რომ ეს \(\vec{f}_{R}\) ძალა წონასწორდება ბირთვზე მოქმედი მეორე ძალით, რომელიც სწორედ კორიოლისის ძალას წარმოადგენს.

            განვიხილოთ m მასის მატერიალური წერტილი, რომელიც მოძრაობს დისკოს მიმართულებით \(\vec{v}\)სიჩქარით. დისკოს ბრუნვის კუთხის სიჩქარე აღვნიშნოთ \(\vec{\omega }\)-თი და გამოვთვალოთ კორიოლისის ძალის სიდიდე. რადგან წერტილი მოძრაობს რადიალურად, ამიტომ ცხადია, რომ დისკოს ბრუნვის გამო წერტილის სიჩქარე დისკოს მიმართ იცვლება როგორც სიდიდით, ისე მიმართულებით. განვიხილოთ ეს ცვლილებები ცალ-ცალკე.

            წერტილის \(\vec{v}\) სიჩქარის რადიალური მდგენელი დისკოს მიმართ უცვლელი რჩება სიდიდით და მხოლოდ მობრუნდება მის მიმართ \(\omega\) კუთხური სიჩქარით დისკოს ბრუნვის საწინააღმდეგო მიმართულებით. ეს განაპირობებს ნორმალურ აჩქარებას

\(a^{_{n}}=\frac{v^{2}}{r}=\frac{vr\omega }{r}=v\omega\)

რომელიც OA რადიუსის პერპენდიკულარულია. ესაა წერტილის აჩქარების პირველი მდგენელი, რომელიც წერტილის სიჩქარის მიმართულების ცვლილებას გამოსახავს.

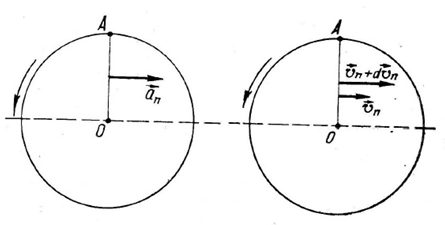
ვთქვათ dt დროში r იცვლება r-დან r+dr-მდე, სადაც dr = vdt. წერტილის სიჩქარის მდგენელი, რომელიც რადიუსის მართობული (\(v_{n}=\omega r\)), გაიზრდება dt დროში სიდიდით \(dv_{n}=\omega dr=\omega vdt\). სიჩქარის ამ ცვლილების შესაბამისი აჩქარება

\(a_{i}=\frac{\mathrm{d} v_{n}}{\mathrm{d} t}=\omega v\)

რაც აჩქარების მეორე მდგენელს წარმოადგენს და იგი სიჩქარის სიდიდის ცვლილებას გამოსახავს.

            გამოდის რომ აჩქარების ორივე მდგენელი ერთმანეთის ტოლია  და ერთნაირი მიმართულებისაა, რის გამოც სრული აჩქარება

\(a_{k}=2\omega v\)

ამ აჩქარებას კორიოლისის აჩქარება ეწოდება.

            მტკიცდება, რომ მიღებული ფორმულა მართებულია მბრუნავ დისკოზე წერტილის არა მარტო რადიალური, არამედ ნებისმიერი მიმართულებით მოძრაობის შემთხვევაში. თუკი წერტილის სიჩქარე \(\vec{v}\)ვექტორი ადგენს ბრუნვის ღერძთან \(\alpha\) კუთხეს, მაშინ კორიოლისის აჩქარება ტოლია

\(a_{k}=2\omega v\sin \alpha\)

ამასთან ყველა შემთხვევაში \(\vec{a}_{k}\) მართებულია \(\vec{v}\) და \(\vec{\omega }\) ვექტორებისა და მათთან ერთად ადგენს მარჯვენა სისტემას. ამის გამო კორიოლისის აჩქარების ვექტორი

\(\vec{a}_{k}=2\left [ \vec{v}\cdot \vec{\omega } \right ]\)

აქედან კორიოლისის ძალა

\(\vec{F}_{k}=2m\left [ \vec{v}\cdot \vec{\omega } \right ]\)

რადგან დედამიწა წარმოადგენს მბრუნავ სისტემას, ამიტომ კორიოლისის ძალის მოქმედებას ჩვენ ბევრ მოვლენაში ვხვდებით.

მოამზადა: ელენე ფილიშვილმა

ხშირად ბუნებაში ვხვდებით ისეთ შემთხვევებს, როდესაც ურთიერთქმედების არსებობის მიუხედავად ნივთიერი წერტილი ან სხეული უძრავი რჩება.  ნივთიერი წერტილი წონასწორობაშია, თუ იგი, მოყვანილი უძრავ მდგომარეობაში, უძრავი რჩება შემდეგშიც.

ის პირობა, რომ ნივთიერი წერტილი უნდა იყოს უძრავ მდგომარეობაში ადვილი შესასრულებელია, რადგან დაკავშირებულია საყწისი პირობების შერჩევასთან. წონასწორობისთვის მნიშვნელოვანია მეორე პირობა, რომ ნაწილაკმა არ უნდა დაიწყოს მოძრაობა, ანუ მისი აჩქარება უნდა იყოს ნულის ტოლი 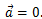 . მოძრაობის კანონების თანახმად  

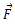
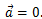
სადაც   არის ნაწილაკზე მოქმედი ძალების ჯამი. რადგან წონასწორობაში

 მივიღებთ, რომ

წონასწორობისთვის საჭიროა ნაწილაკზე მოქმედი ძალების ჯამი იყოს ნულის ტოლი. და პირიქით, თუ ნაწილაკზე მოქმედი ძალების ჯამი ნულის ტოლია, ნაწილაკი წონასწორობაშია.   ამ განტოლების ღერძებზე დაგეგმილებით მივიღებთ:

ე.ი. წონასწორობისთვის საჭიროა, რომ ნულის ტოლი იყოს ყოველ ღერძზე ძალების გეგმილების ჯამი.

წონასწორობის პირობები შეგვიძლია ჩავწეროთ პოტენციური ენერგიის გამოყენებითაც:

წონასწორობის შემთხვევაში შემდეგი პირობები უნდა სრულდებოდეს:

ე.ი. წონასწორობის მდებარეობაში პოტენციალური ენერგიის კოორდინატებით კერძო წარმოებულები ნულის ტოლი უნდა იყოს.

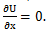
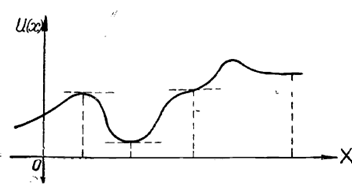
განვიხილოთ მარტივი შემთხვევა, როდესაც ნაწილაკი მოძრაობს მხოლოდ OX ღერძზე, მაშინ  გვექნება მხოლოდ      როგორც ცნობილია მათანალიზიდან, ფუნქციის წარმოებული თუ ნულის ტოლია რაიმე წერტილში მაშინ ფუნქციას აქვს ან ექსტრემუმი (მინიმუმი ან მაქსიმუმი) ან გადაღუნვის წერტილი ან ფუნქცია მუდმივია ამ წერტილის მახლობლობაში.

დავხაზოთ პოტენციური ენერგიის, როგორც x-ის ფუნქციის გრაფიკი, პოტენციალური მრუდი.

პოტენციალური მრუდი გვაძლევს არა მარტო პოტენციურ ენერგიას, არამედ წერტილზე მოქმედი ძალის მნიშვნელობასაც. ამისათვის საკმარისია აღებულ წერტილზე გავატაროთ მხები და გავზომოთ ამ მხებით შექმნილი კუთხე OX ღერძთან. ამ კუთხის ტანგესი მინუს ნიშნით გვაძლევს ნაწილაკზე მოქმედი ძალის მნიშვნელობას. წონასწორობაში

ე.ი. წონასწორობის სათანადო წერტილში მხები აბსცისთა ღერძის პარალელური უნდა იყოს. ნახაზი გვიჩვენებს, რომ ამას ადგილი აქვს მაქსიმუმის, მინიმუმის ან გადაღუნვის წერტილებში, ან ისეთ ნაწილში, სადაც მრუდი აბსცისთა ღერძის პარალელურია.

წონასწორობის მდებარეობიდან გამოყვანილი ნაწილაკის მოძრაობის ხასიათი განსხვავებული შეიძლება იყოს.

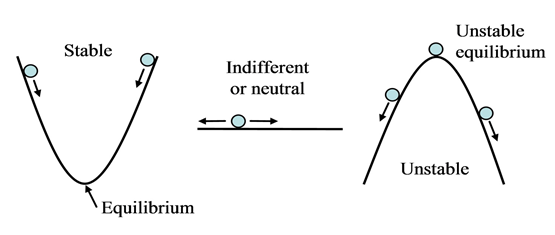
განვიხილოთ ჩაზნექილი ჭურჭლის ყველაზე დაბალ მდებარეობაში მოთავსებული ბირთვი, თუ მას წონასწორობის მდგომარეობიდან გამოვიყვანთ ის დაიწყებს რხევას წონასწორობის მდებარეობის მახლობლად. სხვანაირად იმოძრავებს ბირთვი, რომელიც ამოზნექილი ჭურჭლის ყველაზე მაღალ ადგილასაა მოთავსებული და გამოყვანილია წონასწორობის მდგომარეობიდან. ის კი არ დაუბრუნდება წონასწორობის ამ მდებარეობას, არამედ განაგრძობს დაშორებას ამ მდებარეობიდან. განვიხილოთ ისეთი შემთხვევა როდესაც ბირთვი წონასწორობაშია ბრტყელ ჰორიზონტულ ზედაპირზე. თუ გამოვიყვანთ ამ მდგომარეობიდან ის წონასწორობაში იქნება ახალ მდებარეობაშიც, რაც ნიშნავს, რომ ახალი მდებარეობაც წონასწორობის მდგომარეობას წარმოადგენს. 

 

 

შეგვიძლია შემოვიღოთ წონასწორობის მდებარეობათა შემდეგი კლასიფიკაცია:

• მდგრადი წონასწორობა:  თუ წონასწორობიდან გამოყვანილი ნივთიერი წერტილი საკმაოდ მცირე ბიძგით ან გადახრით ისევ ამ მდგომარეობას უბრუნდება.
• არამდგრადი წონასწორობა:  როდესაც ნივთიერი წერტილი წონასწორობიდან გამოყვანის შემდეგ განაგრძობს ამ მდებარეობიდან დაშორებას.
• განურჩეველი წონასწორობა:  როდესაც წონასწორობის მახლობელი მდებარეობები ისევ წონასწორობის მდებარეობებს წარმოადგენენ.

 

დავაკავშიროთ წონასწორობის ეს სახეები პოტენციურ მრუდთან. ავღნიშნოთ x₀-ით მინიმუმის წერტილის შესაბამისი კოორდინატი, პოტენციური ენერგია ამ წერტილში იქნება 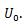.  ამ მდებარეობაში მყოფ ნაწილაკს მივანიჭოთ სიჩქარე v₀ და კინეტიკური ენერგია \(T_{0}=\frac{mv^{_{2}}}{2}\).   ნაწილაკის სრული ენერგია ბიძგის შემდეგ იქნება:

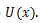
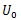
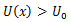
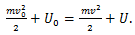
გარკვეული დროის შემდეგ ნაწილაკი გადავა ახალ მდებარეობაში კოორდინატით x და პოტენციური ენერგიით .  რადგან  პოტენციური ენერგიის მინიმალური მნიშვნელობაა, ცხადია,  რომ  .  მეორეს მხრივ, ენერგიის მუდმივობის კანონის თანახმად      .

აქედან მივიღებთ: 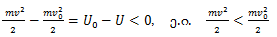, რაც იმას ნიშნავს, რომ ნაწილაკის კინეტიკური ენერგია შემცირდა, როდესაც იგი წონასწორობის მდებარეობიდან მეზობელ მდებარეობაში გადავიდა. მინიმალური პოტენციალური მდებარეობიდან გამოსული ნაწილაკი თანდათან ამცირებს თავის სიჩქარეს. დადგება მომენტი, როდესაც ნაწილაკი გაჩერდება და მასზე მოქმედი ძალების გავლენით დაბრუნდება საწყის მდგომარეობაში. ეს კი ნიშნავს, რომ მინიმალური პოტენციური ენერგიის მდებარეობას შეესაბამება მდგრადი წონასწორობა. ანალოგიურად შეიძლება დამტკიცდეს, რომ პოტენციალური ენერგიის მაქსიმუმს შეესაბამება არამდგრადი წონასწორობა. იმ შემთხვევაში, როდესაც პოტენციალური ენერგია უცვლელია ნაწილაკი გადახრის შემდეგ დარჩება იგივე მდგომარეობაში, რაც ნიშნავს, რომ ყველა მეზობელი მდებარეობა იქნება წონასწორობის მდებარეობა და გვექნება განურჩეველი წონასწორობა.

პოტენციური ენერგიის მრუდის გადაღუნვის წერტილში მხები აბსცისთა ღერძის პარალელურია, მაგრამ ამ წერტილის ერთ მხარეს პოტენციალური ენერგია მატულობს, მეორე მხარეს კი კლებულობს.

თუ წონასწორობის მდებარეობიდან ნაწილაკს გადავხრით იმ მხარეს, რომლის მიმართულებითაც პოტენციური ენერგია კლებულობს, ნაწილაკი სულ უფრო დაშორდება საწყის მდებარეობას. თუ ნაწილაკს გადავხრით პოტენციური ენერგიის ზრდის მიმართულებით, იგი თანდათან შეანელებს მოძრაობას, გაჩერდება და დაუბრუნდება საწყის მდებარეობას, გადასცდება და სულ უფრო და უფრო დაშორდება მას, ამ შემთხვევაშიც წონასწორობა იქნება არამდგრადი.

 

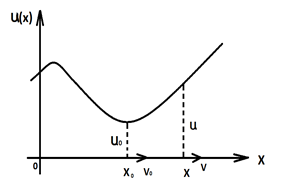
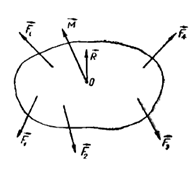
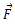
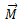
განვიხილოთ მყარი სხეულის შემთხვევა. მყარ სხეულზე მოქმედი ძალები შეგვიძლია დავიყვანოთ ერთ ძალაზე ან ერთ ძალთა წყვილზე. თუ მარეზულტირებელ ძალას და მომენტს ავღნიშნავთ სათანადოდ  და  -ით, მოძრაობის განტოლებები შემდეგი სახით ჩაიწერება:

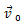
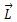
სადაც m არის მყარი სხეულის მასა,   - ინერციის ცენტრის სიჩქარე და  - იმპულსის მომენტი. გამოვიყენოთ წონასწორობის იგივე განსაზღვრა, რაც ნივთიერი წერტილის შემთხვევაში. თუ მყარი სხეული უძრავ მდგომარეობაშია და იგი არ გამოდის ამ მდებარეობიდან იგი წონასწორობაშია. ვინაიდან მყარ სხეულს შეუძლია შეასრულოს გადატანითი და ბრუნვითი მოძრაობა წონასწორობის მდებარეობაში არც ერთი მათგანი არ უნდა დაიწყოს. ეს იმას ნიშნავს, რომ ინერციის ცენტრის აჩქარება ნულის ტოლი უნდა იყოს და არ უნდა იცვლებოდეს იმპულსის მომენტი

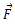
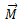
ამისთვის საჭიროა გარეშე ძალების  ჯამის და   ჯამის ნულთან ტოლობა

რაც წარმოადგენს წონასწორობის პირობას მყარი სხეულის შემთხვევაში. პირველი პირობა ისეთივეა, როგორც ნივთიერი წერტილის წონასწორობის პირობა და ამიტომ მის მიმართაც შეგვიძლია გავიმეოროთ ყველაფერი რაც ნივთიერი წერტილისთვის. შედარებით საინტერესო და მნიშვნელოვანია მეორე პირობა, რომელიც კრძალავს ბრუნვის დაწყებას. 

ვექტორული განტოლება შეგვიძლია დავშალოთ სამ სკალარულ განტოლებად, თუ დავაგეგმილებთ მას კოორდინატთა ღერძებზე. მივიღებთ

\(\vec{M}=0\)

რაც ნიშნავს, რომ საერთო მომენტის გეგმილები ღერძებზე ნულის ტოლი უნდა იყოს.

განვიხილოთ ზოგადი წონასწორობის პირობების ზოგიერთი კერძო შემთხვევა. ჩვეულებრივ პრაქტიკაში საჭიროა მყარი სხეულის წონასწორობის პირობების დადგენა იმ შემთხვევაში, როდესაც მყარი სხეული არ არის თავისუფალი, ე.ი. როდესაც მისი მოძრაობა შეზღუდულია გარეშე სხეულებით-ბმებით. ამ შემთხვევაში უშუალოდ მიღებულ ძალებს უნდა დაემატოს რეაქციის ძალები, ე.ი. ძალები, რომლებითაც გარეშე სხეულები მოქმედებენ განსახილველ სხეულზე.

 

განვიხილოთ მყარი სხეული, რომელსაც შეუძლია ბრუნვა უძრავი ღერძის ირგვლივ. ასეთ სხეულს ბერკეტი ეწოდება.

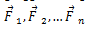
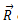
ვთქვათ, ბერკეტზე მოქმედებენ ღერძისადმი მართობულ სიბრტყეში მდებარე  ძალები. გარდა ამ ძალებისა, ბერკეტზე მოქმედებს კიდევ ღერძი რეაქციის  ძალით. წონასწორობის პირობის თანახმად, მოქმედი ძალების ჯამი უნდა იყოს ნულის ტოლი:

ეს  პირობა საშუალებას იძლევა ვიპოვოთ რეაქციის ძალა.

წონასწორობის მეორე პირობა - ძალთა მომენტების ჯამის ნულთან ტოლობა ჩაიწერება შემდეგნაირად:

 

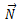
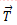
კედელზე ჩამოკიდებული სფერო:  ვერტიკალურ კედელზე  L სიგრძის თოკზე ჩამოკიდებულია m მასის სფერო, რომლის რადიუსია R.  იპოვეთ სფეროზე მოქმედი რეაქციის   და თოკის დაჭიმულობის  ძალები. ხახუნი კედელთან უგულებელყავით.

წონასწორობის პირობის თანახმად სფეროზე მოქმედ ძალთა ტოლქმედი ნულის ტოლია: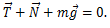    

 

ნახაზზე მოცემულ კოორდინატთა ღერძებზე  დაგემილებით მივიღებთ განტოლებათა შემდეგ სისტემას: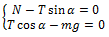 

როგორც ვხედავთ ეს ორი განტოლება საკმარისი არ არის საძიებელი ძალების გამოსათვლელად.  გვჭირდება კიდევ ერთი განტოლება. ამ განტოლებას წარმოადგენს წონასწორობის მეორე პირობა – მომენტების წესი. ავირჩიოთ რომელიმე ბრუნვის ღერძი. ამოცანის პირობიდან გამომდინარე ადვილი მისახვედრია, რომ მოხერხებულია ბრუნვის ღერძად ავირჩიოთ სფეროს ცენტრზე ნახაზის სიბრტყის მართობულად გამავალი ღერძი. ამ ღერძის მიმართ რეაქციის და სიმძიმის ძალების მომენტები ნულის ტოლია, რადგან მათი მოქმედების წრფე გადის ბრუნვის ღერძზე. 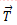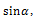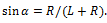მაშასადამე თოკის დაჭიმულობის  ძალის მოქმედების წრფეც უნდა გადიოდეს სფეროს ცენტრზე, წინააღმდეგ შემთხვევაში ეს ძალა გამოიწვევდა სფეროს ბრუნვას. ამრიგად თოკის დაჭიმულობის ძალაც რეაქციის და სიმძიმის ძალების მსგავსად სფეროს ზედაპირის მართობულად მოქმედებს. ეს საშუალებას გვაძლევს გამოვთვალოთ ,   კერძოდ .  განტოლებათა სისტემის ამოხსნით

მივიღებთ:

 

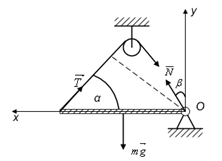
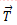
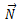
თოკით გაწონასწორებული ჰორიზონტული ღერო: m=30 კგ მასის ერთგვაროვანი ღერო,  რომელიც სახსრულად არის დამაგრებული  O წერტილში და რომელსაც შეუძლია ბრუნვა ხახუნის გარეშე, ჰორიზონტულად არის გაჩერებული ჭოჭონაქზე გადაკიდებული თოკით.  თოკი ღეროსთან ადგენს α=60◦C  კუთხეს. გამოთვალეთ თოკის დაჭიმულობის   და ღეროზე სახსარში მოქმედი რეაქციის  ძალები (ნახ. 2). ჩათვალეთ  g=10მ/წმ².

აქ უნდა მივიღოთ მხედველობაში, რომ სახსარში რეაქციის ძალა მიმართულია რაღაც β კუთხით ვერტიკალის მიმართ. მისი ერთი მდგენელი N_x მოქმედებს ღეროს გასწვრივხოლო მეორე N_y  მის მართობულად . მდგენელებით ვიპოვნით რეაქციის ძალის როგორც სიდიდეს, ასე მის მიმართულებას – β კუთხეს, კერძოდ

.

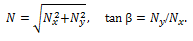
გამოვიყენოთ წონასწორობის პირობები. ღეროზე მოქმედი ძალებია რეაქციის, სიმძიმის და თოკის დაჭიმულობის ძალები. წონაწორობის პირობა გეგმილებში შემდეგნაირად ჩაიწერება:

ეს ორი განტოლება შეიცავს სამ უცნობს, მესამე განტოლების სახით გამოვიყენოთ მომენტების წესი. ბრუნვის ღერძად ავირჩიოთ სახსარზე ნახაზის სიბრტყის მართობულად გამავალი ღერძი.  მის მიმართ რეაქციის ძალის მომენტი ნულის ტოლია, დანარჩენი ორი ძალისთვის (რომლებიც სხეულს ანიჭებენ ურთიერთსაპირისპირო მაბრუნებელ ქმედებას) მომენტების წესი ასე გამოიყურება:

d  არის ღეროს სიგრძე. ამ განტოლებიდან მივიღებთ:

ამის შემდეგ პირველი ორი განტოლების ამოხსნა სირთულეს არ წარმოადგენს. საბოლოოდ მივიღებთ:

 

ჩავხაზოთ ცილინდრი სფეროში. ცილინდრის კედლები რომ არ შთანთქავდეს ენერგიას, მასზე დაცემული ენერგია ზუსტად ტოლი იქნებოდა ენერგიისა, რაც გაივლიდა სფეროს ცილინდრით მოჭიმულ სფერულ სარტყელში.

სფეროს რადიუსია

\(R_{s}=\sqrt{R^{2}+(\frac{h}{2})^{2}}\)

სფერული სარტყლის ფართობი

\(S_{s}=2\pi R_{s}h\)

ცილინდრის გვერდითა ზედაპირის ფართობი

\(S_{c}=2\pi Rh\)

სფერულ სარტყელში ნაკადი იქნება

\(\Phi _{s}=P\frac{S_{s}}{4\pi R_{s}^{2}}\)

მაშინ ცილინდრის კედლებზე დაცემული ნაკადი იქნება