x1 წერტილში - \(a_{2}=ae^{-\gamma x_{2}}\)
მაშინ \(\mu =\frac{a_{1}-a_{2}}{a_{1}}=1-exp(\gamma x_{1}-\gamma x_{2})\)
\(exp(\gamma x_{1}-\gamma x_{2})=1-\mu\)
\(x_{1}-x_{2}=\frac{1}{\gamma }ln(1-\mu )\)
ფაზათა შორის სხვაობა იქნება
\(\Delta \varphi =kx_{1}-kx_{2}=k(x_{1}-kx_{2})=\frac{k}{\gamma }ln(1-\mu )\)
\(\Delta \varphi =\frac{k}{\gamma }ln(1-\mu )\)
\(\varphi _{1}=\omega t-\vec{k}\vec{r}_{1}+\varphi _{0}\)
\(\varphi _{2}=\omega t-\vec{k}\vec{r}_{2}+\varphi _{0}\)
ფაზათა შორის სხვაობა იქნება
\(\Delta \varphi =\varphi _{2}-\varphi _{1}=\vec{k}\left (\vec{r}_{2} -\vec{r}_{1} \right )\)
რადგან \)\Delta \varphi =\frac{\omega }{v}\left [ \left ( x_{2}-x_{1} \right )\cos \alpha + \left ( y_{2}-y_{1} \right )\cos \beta + \left ( z_{2}-z_{1} \right )\cos \gamma \right ]$
ამოცანა 8.1
ω სიხშირის ბრტყელი ჰარმონიული ტალღა ვრცელდება v სიჩქარით მიმართულებით, რომელიც x, y, z ღერძებთან ადგენს შესაბამისად α, β, γ კუთხეებს. იპოვნეთ გარემოს x1, y1, z1 და x2, y2, z2 კოორდინატების მქონე წერტილებს შორის ფაზათა სხვაობა.
ამოცანა 8.2
ერთგვაროვან გარემოში ვრცელდება ბრტყელი დრეკადი ტალღა, რომლის გაანტოლება არის ξ = ae-γx(ωt - kx), სადაც a, γ, ω და k — მუდმივებია. იპოვნეთ იმ წერტილებს შორის ფაზათა სხვაობა, რომლებშიც გარემოს ნაწილაკების წანაცვლება ერთმათისგან განსხვავდება η სიდიდით.
ამოცანა 8.3
იზოტროპული წერტილოვანი წყარო, რომლის ბგერითი სიმძლავრე არის P, მოთავსებულია ღრუ R რადიუსისა და h სიმაღლის მქონე ცილინდრის ცენტრში. ვიგულისხმოთ, რომ ცილინდრის კედლები სრულად შთანთქავს ბგერას და იპოვნეთ ენერგიის საშუალო ნაკადი, რომელიც ეცემა ცილინდრის გვერდითა კედლებს.
ამოცანა 7.1
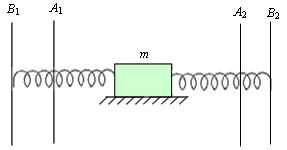 იდეალურად გლუვ ზედაპირზე ძევს m მასის ტვირთი, ორი მხრიდან გაჭიმული 1 და 2 ზამბარით, რომელთა დრეკადობის კოეფიციენტებია k1 და k2. თუ ტვირთს გამოვიყვანთ წონასწორობიდან (გვერდზე გადახრით) იგი დაიწყებს რხევას Т პერიოდით. შეიცვლება თუ არა რხევის პერიოდი, თუ იმავე ზამბარებს დავამაგრებთ არა А1 და А2 წერტილებში არამედ В1 და В2 წერტილებში?
იდეალურად გლუვ ზედაპირზე ძევს m მასის ტვირთი, ორი მხრიდან გაჭიმული 1 და 2 ზამბარით, რომელთა დრეკადობის კოეფიციენტებია k1 და k2. თუ ტვირთს გამოვიყვანთ წონასწორობიდან (გვერდზე გადახრით) იგი დაიწყებს რხევას Т პერიოდით. შეიცვლება თუ არა რხევის პერიოდი, თუ იმავე ზამბარებს დავამაგრებთ არა А1 და А2 წერტილებში არამედ В1 და В2 წერტილებში?
ამოცანა 7.2
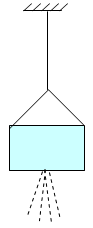 ქანქარა შედგება ძაფზე ჩამოკიდებული წყლით სავსე ჭურჭლისგან. როგორ შეიცვლება ქანქარის პერიოდი, თუ ჭურჭლის ფსკერი გახვრეტილია და იქიდან წყალი გამოდის? 1) როცა თვით ჭურჭლის მასათა ცენტრი არის ფსკერზე და 2) როცა მასათა ცენტრი არის ფსკერს ზემოთ.
ქანქარა შედგება ძაფზე ჩამოკიდებული წყლით სავსე ჭურჭლისგან. როგორ შეიცვლება ქანქარის პერიოდი, თუ ჭურჭლის ფსკერი გახვრეტილია და იქიდან წყალი გამოდის? 1) როცა თვით ჭურჭლის მასათა ცენტრი არის ფსკერზე და 2) როცა მასათა ცენტრი არის ფსკერს ზემოთ.
ამოცანა 7.3
მატერიალური წერტილი მონაწილეობს ერთდროულად ორ ჰარმონიულ რხევით პროცესში, რომლებიც ერთი მიმართულებით მიმდინარეობს. მათი სიხშირეები ტოლია, ამპლიტუდებია x01= 5 სმ და x02= 10 სმ და ფაზათა წანაცვლებაა  . განსაზღვრეთ ჯამური რხევითი პროცესის ამპლიტუდა და საწყისი ფაზა.
. განსაზღვრეთ ჯამური რხევითი პროცესის ამპლიტუდა და საწყისი ფაზა.
ამოცანა 7.4
განსაზღვრეთ l = 20 სმ სიგრძის უჭიმვად, უწონო ძაფზე ჩამოკიდებული ბურთულას მცირე რხევების პერიოდი, თუ სისტემა მოთავსებულია სითხეში, რომლის სიმკვრივე η=3-ჯერ ნაკლებია ბურთულისაზე. სითხის წინაღობა უგულებელვყოთ. (გაიხსენეტ, რომ არქიმედეს ამომგდები ძალა \(\vec{F}_{A}=-\rho _{l}V\vec{g}\), სადაც . \(\rho _{l}\) სითხის სიმკვრივეა).
ამოცანა 7.5
უწონო ზამბარაზე ჩამოკიდებულია ტვირთი და ზამბარა გაჭიმულია Δх = 9,8 სმ სიგრძით. რა პერიოდით დაიწყებს რხევას ტვირთი, თუ მას ოდნავ ვუბიძგებთ ვერტიკალური მიმართულებით? მილევის ლოგარითმული დეკრემენტი არის λ = 3,1.
წერტილოვანი დადებითი მუხტიდან ორჯერ მეტად დაშორებული წერტილის პოტენციალი: ა. ორჯერ მეტია ბ. ორჯერ ნაკლებია გ. ოთხჯერ მეტია დ.ოთხჯერ ნაკლებია რომელია სწორიი? ჯერ, ორჯერ დაშორებულიო........
გლუვ არაგამტარ ჰორიზონტალურ ზედაპირზე მოთავსებული ერთი ნიშნით დამუხტული ორი 1კგ მასის ბურთულა გადაბმულია 1მეტრი სიგრძის უწონო თოკით, თოკის დაჭიმულობის ძალაა 200 ნიუტონი, თოკი გადაჭრეს, რისი ტოლი გახდე........
მოგესალმებით, იპოვეთ ელექტრონთა მოწესრიგებული მოძრაობის სიჩქარე 25მმ2 განივკვეთის სპილენძის გამტარში, თუ დენის ძალა 50ა. ჩათვალეთ, რომ თითოეულ ატომზე მოდის გამტარობის ერთი ელექტრონი
როგორც ჩანს იმდენი დრო არ გაქვთ იმ კითხვებზე რომ მიპასუხოთ და იქნებ ამაში გამარკვიოთ.. როცა მეკითხებიან წნევას h სიღრმეზე, რომელ ფორმულას ვიყენებთ P=Pატმ+þgh თუ P=þgh? და როდესაც ვწერ........

