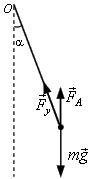
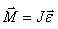
სადაც \(J\) - ქამქარის ინერციის მომენტია, M - ძალების ჯამური მომეტი, ხოლო \(\varepsilon =\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}\) არის კუთხური აჩქარება. რადგან დაჭიმულობის ძალის მოქმედების წრფე გადის ბრუნვის ღერძზე, მისი მომენტი ნულის ტოლია. სიმძიმის ზალის მომენტი იქნება M1 = mglsinα, არქიმედის ძალის მომენტი კი - M2 = FAlsinα . აქედან გამომდინარე მოძრაობის განტოლებას ექნება სახე
\(ml^{2}\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}=\left ( mg-F_{A}\right )l\sin \alpha\) . (2)
გავითვალისწინოთ, რომ m = ρV, სადაც ρ- ბურთულის მასალის სიმკვრივეა, ხოლო \(\vec{F}_{A}=-\rho _{l}V\vec{g}\)და ასევე მცირე კუთხეებისთვის sinα ≈ α, მაშინ განტოლება (2) მიიღებს სახეს:
.\(\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}+\frac{\left (\eta -1\right )}{l\eta }g \alpha=0\)
ეს არის ჰარმონიული რხევის განტოლება და რხევის სიხშირე არის \(\omega _{0}=\sqrt{\frac{\left (\eta -1\right )}{l\eta }g}\) .
პერიოდი იქნება \(T=\frac{2\pi }{\omega _{0}}\)
ჩავსვათ შესაბამისი რიცხვები.