ამოცანის ამოხსნისთვის მოსაახერხებელია გამოვიყენოთ რხევების წარმოდგენის  გრაფიკული მეთოდი. განსახილველი რხევების მოძრაობის კანონები ჩაიწერება ასე: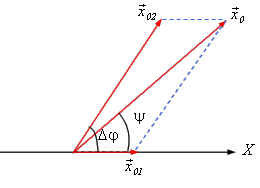

x₁ = x₀₁cosωt,

x₂ = x₀₂cos(ωt + Δφ)

სადაც x₀₁ და x₀₂ - არის მერხევი ნაწილაკის წანაცვლებები წონასწორობის მდგომარეობიდან. პირველი რხევითი პროცესის საწყისი ფაზა ჩათვლილია ნულად. რადგან სიხშირეები ტოლია, ამიტომ რხევების გამომსახველ ვექტორებს შორის კუთხე არ იცვლება დროში. ამიტომ ვექტორული დიაგრამა შეიძლება აიგოს t = 0 მომენტისთვის. ნახაზიდან ჩანს, რომ

x₀₂ = x₀₁₂ + x₀₂₂ + 2x₀₁x₀₂cosΔφ.

უკანასკნელი გამოსახულება გამომდინარეობს კოსინუსების თეორემიდან. ჩავსვათ რიცხვითი მნიშვნელობები და მივიღებთ x₀= 13 სმ. ჯამური რხევის საწყისი ფაზა ტოლი იქნება Х ღერძსა და ჯამური რხევის \(\vec{x}_{0}\) ვექტორს შორის  ψ კუთხის. გეომეტრული მოსაზრებებიდან ჩანს, რომ

. \(tg\psi =\frac{x_{02\sin \Delta \varphi }}{x_{01}+x_{02}\cos \Delta \varphi }\)
აქედან ψ = 0,23. 
საბოლოოდ ჯამური რხევა ჩაიწერება ასე:

x = 13 cos(ωt + 0,23π).

პასუხი: x₀= 13 სმ;   \(tg\psi =\frac{x_{02\sin \Delta \varphi }}{x_{01}+x_{02}\cos \Delta \varphi }\).