პირველი წარმოდგენა სინათლის ბუნების შესახებ ძველ საბერძნეთსა და ეგვიპტეში შეიმნა. ოპტიკური ხელსაწყოების გამოგონებითა და განვითარებით (პარაბოლური სარკე, მიკროსკოპი, ტელესკოპი) ეს წარმოდგენა ვითარდებოდა და იცვლებოდა. XVII საუკუნის ბოლოს წარმოიშვა ორი თეორია: კორპუსკულული (ი.ნიუტონი) და ტალღური (რ.ჰუკი და ქ.ჰიუგენსი).
კორპუსკულური თეორიის თანახმად, სინათლე წარმოადგენს ნაწილაკების (კორპუსკულების) ნაკადს, რომლებიც მნათი სხეულებიდან გამოდიან. ნიუტონი თვალიდა, რომ სინათლის კორპუსკულების მოძრაობა მექანიკის კანონებს ემორჩილებოდნენ. ამის მიხედვით, სინათლის არეკვლა დრეკადი ბურთულას არეკვლის ანალოგიურია, სინათლის გარდატეხა იხსნებიდა კორპუსკულების სიჩქარის ცვლილებით ერთი გარემოდენ მეორეში გადასვლისას. სინათლის ვაკუუმსა და გარემოს შორის გარდატეხის შემთხვევისთვის კორპუსკულური თეორია გარდატეხის კანონის შემდეგ სახეს იძლეოდა:
სადაც c – ვაკუუმში სინათლე სიჩქარეა, υ – სინათლის გარემოში გავრცელების სიჩქარე. რადგან n > 1, კორპოსკულური თეორიიდად გამოდიოდა რომ სინათლის სიჩქარე გარემოში მეტი უნდა იყოს ვიდრე ვაკუუმში. ნიუტონი ასევე ცდილობდა ინტერფერენციული ზოლების წარმოქმნა სინათლის პროცესებში გარკვეული პერიოდულობის შემოტანის საშუალებით. ამგვარად, ნიუტონის კორპუსკულური თეორია გარკვეულ ტალღურ წარმოდგენებს შეიცავდა.
ტალღური თეორია, კორპოსკულურისგან განსხვავებით, სინათლეს განიხილავს, როგორც მექანიკური ტალღების მსგავს ტალღურ პროცესს. ტალღური თეორიას საფუძვლად დაედო ჰიუგენსის პრინციპი, რომლის მიხედვითაც ყოველი წერტილი რომლამდეც ტალღა აღწევს, მეორადი ტალღის ცენტრი ხდება, ხოლო ამ ტალღების შემომწერი (A1A2 სიბრტყე ნახ. 1-ზე) იძლევა დროის შემდეგ მომენტში ტალღის ფრონტის მდებარეობას. ტალღის ფრონტში გეი-ლუსაკი გულისხმობდა იმ წერტილების გეომეტრულ ადგილს, რომლებამდეც ტალღური შეშფოთება ერთდროულად აღწევს. ამ პრინციპის საშუალებით იქნა ახსნილი არეკვლისა და გარდატეხის კანონები. ნახ. 1-ზe წარმოდგენილია ჰიუგენსის აგებები ორი გამჭვირვალე გარემოს გამყოფ ზედაპირზე გარდატეხილი ტალღის გარკვეული მიმართულებით გავრცელებისთვის.
ნახ. 1.
ჰიუგენსის აგება გარდატეხილი ტალღის გარკვეული მიმართულებისთვის.
სინათლის ვაკუუმსა და გარემოს შორის გარდატეხის შემთხვევისთვის ტალღური თეორია შემდეგ დასკვნამდე მიდის:
ტალღური თეორიიდან მიღებული გარდატეხის კანონი ნიუტონის ფორმულას ეწინააღმდეგება. ტალღურ თეორიას მივყავართ დასკვნამდე: υ < c, მაშინ როცა, კორპუსკულური თეორიის თანახმად υ > c.
ამგვარად. XVIII საუკუნის დასაწისში არსებობდა სინათლის ბუნების ორი ურთიერთსაწინააღმდეგი მიდგომა: ნიოტონის კორპუსკულური თეორია და ჰიუგენსის ტალღური თეორია. ორივე ხსნიდა სინათლის წრფივ გავრცელებას, არეკვლისა და გარდატეხის კანონებს. მთელი XVIII საუკუნე ამ ორი თეორიის ბრძოლის საუკუნედ იქცა. მაგრამ XIX საუკუნის დასაწყისში სიტუაცია მთლიანად შეიცვალა. კორპუსკულური თეორია უარყვეს და ტალღურმა თეორიამ იზეიმა. ამაში დიდ წვლილი ინგლისელ ფიზიკოსს თ.იუნგს და ფრაგ ფიზიკოს ო.ფრენელს მიუძღვით მათ ინტერფერენციის და დიფრაქციის მოვლენები შეისწავლეს. ამ მოვლენების ამომწურავი ახსნა მხოლოს ტალღურ თეორიას შეეძლო. ტალღური თეორიის სამართლიანობის მნიშვნელოვანი ექსპერიმენტული დასაბუთება იყო 1851 წელს ჟ.ფუკოს (და მისგად დამოუკიდებლად ა.ფიზოს) მიერ წყალში სინათლის გავრცელების სიჩქარის გაზომა და მან მიიღო υ < c მნიშვნელოვა.
მიუხედავადიმისა, რომ XIX საუკუნის შუა წლებში ტალღური თეორია საყოველთაოდ მიღებული იყო, საკითხი სინათლის ბუნების შესახებ მაინც ღია რჩებოდა.
XIX საუკუნის 60-იან წლებში მაქსველმა დაადგინა ელექტრომაგნიტური ტალღების საერთო კანონი, საიდანაც მან დაასკვნა, რომ სინათლე ელექტრომაგნიტური ტალღაა. ასეთი თვალსაზრისის მნიშვნელოვანი დასაბუთება სინათლის ვაკუუმში გავრცელების სიჩქარისა და ელექტრომაგნიტურ მუდმივასთან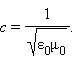 
დამთხვევა შეიქმნა. სინათლის ელექტრომაგნიტურმა ბუნებამ ჰერცის ელექტომაგნიტური ტალღების კვლევისთვის ჩატარებული ცდების შემდეგ საყოველთაო აღიარება მოიპოვა (1887-1888).
სინათლის ბუნების გარკვევაში მნიშვნელოვანი როლი შეასრულა მისი სიჩქარის ცდისეულმა გაზომვებმა. XVII საუკუნის ბოლოდან მოყოლებული სინათლის სიჩქარის სახვადასხვა მეთოდით გაზომვის არაერთი ცდა იქნა ჩატარებული (ა.ფიზოს ასტრონომიული მეთოდი, მაიკელსონის მეთოდი). თანამედროვე ლაზერული ტექნიკა სინათლის სიჩქარის ძალიან დიდი სიზუსტით გაზომვის საშუალებას იძლევა, ტალრის λ სიგრძისა სინათლის ν სიხშირის დამოუკიდებელი გაზომვების ხარჯზე (c = λ · ν). ამგვარი გზით იქნა ნაპოვლი მნიშვნელობა
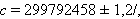
რომელიც სიზუსტით ყველა ადრე მიღებულ მნიშვნელობას ორი რიგით მაინც ჯობნის.
სინათლე ჩვენს ცხოვრებაში განუზომელად დიდ როლს ასრულებს. გარემომცველი გარემოს შესახებ ინფორმაციის ყველაზე მეტ ნაწილს ადამიანი სინათლის საშუალებით იღებს. მაგრამ, ფიზიკის ნაწილში, რომელსაც ოპტიკას ვუწოდებთ, სინათლეში არა მხოლოს ხილული სინათლე იგულისხმება, არამედ მისი მიმდებარე ელექტრომაგნიტური გამოსხივების სპექტრის ფართო დიაპაზონიც - ინფრაწიტელიდან ულტრაიისფერამდე. თვისებების მიხედვით სინათლე პრინციპულად არ განირჩევა ელექტრომაგნიტური გამოსხივების სხვა დიაპაზონებისაგან. სპექტრის სხვადასხვა უბნები ერთმანეთისაგან მხილოდ ტალღის სიგრძითა λ და სიხშირით ν განსხვავდებიან. ნახ. 2-ზე ელექტრომაგნიტური ტალღების შკალაა მოცემული.
ნახ. 2.
ელექტრომაგნიტური ტალღების შკალა. სხვდასხვა დიაპაზონებს შორის საზღვრები პირობითია
ოპტიკურ დიაპაზომში ტალღის სიგრძის გასაზომად გამოიყენება სიგრძის ერთეულები ნანომერტი (ნმ) და მიკრომეტრი (მკმ):
1 ნმ = 10–9 მ = 10–7 სმ = 10–3 მკმ.
ხილული სინათლე დაახლოებით 400-780 ნმ ან 0,40-0,78მკმ დიაპაზონს იკავებს.
სინათლის ელექტრიმაგნიტურმა თეორიამ მრავალი ოპტიკური მოვლენა ახსნა, როგორიცაა ინტერფერენცია, დიფრაქცია, პოლარიზაცია და ა.შ. მაგრამ ამ თეორიამ ვერ შეძლო სინათლის ბუნების ბოლომდე შეცნობა. უკვე XX საუკუნის დასაწყისში გაირკვა, რომ ეს თეორია საკმარისი არ არის ატომის მასშტაბის იმ მოვლენების ასახსნელად, რომლებსაც სინათლის ნივთიერებასთან ურთიერთქმედებისას აქვთ ადგილი. ისეთი მოვლენების შესწავლისთვის, როგორიცაა შავი სხეულის გამოსხივება, ფოტოეფექტი, კომპრონის ეფექტი და სხვა აუცილებელი გახდა ქვანტური წარმოდგენების შემოტანა. მეცნიერება ისევ დაიბრუნდა იდეას კორპუსკულების - სინათლის ქვანტების შესახებ. ის ფაქტი, რომ სინათლე ზოგ ცდაში ტალღურ ბუნებას ავლენს, ხოლო ზოგში კი კორპუსკულურს, ნიშნავს, რომ მას რთული ორმაგი გუნება აქვს, რომელსაც ახასიათებენ ტერმინით კორპუსკულურ-ტალღური დუალიზმი.